DZIEJE RELIGII, FILOZOFII I NAUKI
indeks |
antologia religijna |
antologia filozoficzna |
filozofia nauki
Wojciech Sady: wykłady
Wojciech Sady
Naukowcy hellenistyczni
z: Dzieje religii, filozofii i nauki: od Talesa z Miletu
do Mahometa, Marek Derewiecki 2010
1. Elementy Euklidesa
2. Biologia i medycyna Herofilosa z Chalkedonu i Erasistratosa z Keos
3. Wynalazki Ktesibiosa z Aleksandrii i Filona z Bizancjum
4. Arystarch z Samos o niebie
5. Archimedes z Syrakuz o liczbie π, polach figur,
objętościach brył, a także o statyce i prawie wyporu
6. O pomiarze Ziemi Eratostenesa z Kyrene
7. Apollonios z Perge o krzywych stożkowych i o niebie
8. Trygonometria i astronomia Hipparcha z Nikai
Wraz z podbojami Aleksandra Wielkiego sytuacja
społeczna i polityczna w Helladzie, Egipcie i na Bliskim Wschodzie zmieniła się
dogłębnie i nieodwracalnie. Skończyła się epoka helleńskich miast-państw,
jednocześnie najpotężniejsze wcześniej w rejonie Bliskiego Wschodu imperium
perskie zostało rozbite. Aleksander – uczeń Arystotelesa, który nie ruszał na
wyprawy bez poematów Homera – działał w poczuciu misji cywilizacyjnej i
kulturowej. Na podbitych terenach zakładał miasta na wzór helleński, a grekę
podniósł do rangi języka urzędowego. Jednocześnie mieszał w wojsku i
administracji Macedończyków i Hellenów z Persami, propagując postawy
kosmopolityczne. W rezultacie na rozległym obszarze greka stała się językiem
oficjalnym, liczne ludy przyswoiły sobie helleński dorobek w zakresie sztuki,
literatury i filozofii, po czym same zaczęły wnosić do niego wkład, mieszając
greckie style z własnymi tradycjami. Hellenowie, siłą rzeczy, też zaczęli
przyswajać sobie poglądy i zwyczaje innych narodów – tym bardziej, że względny
dostatek i bezpieczeństwo sprzyjały podróżom. Na obszarze od Hellady i Egiptu po
Persję rozwijać się zaczęła eklektyczna i kosmopolityczna kultura, zwana
hellenistyczną.
W 331 r. p.n.e. Aleksander u ujścia z jednej
odnóg Nilu do Morza Śródziemnego założył Aleksandrię. Po jego nagłej śmierci w
323 r. p.n.e. nastał okres walk o władzę, w wyniku których stworzone przezeń
imperium rozpadło się na kilka dużych – i stosunkowo trwałych – państw. Królem
Egiptu został w 304 r. p.n.e. Ptolemeusz I Soter. Dysponując wielkimi dochodami,
zwłaszcza z handlu zbożem, założył w Aleksandrii Bibliotekę (od greckiego
byblos,
czyli papirus) – która miała
stać się największym księgozbiorem świata starożytnego. Wkrótce potem w mieście
utworzono Muzeum (Musejon,
czyli miejsce poświęcone muzom). Nie jest jasne, czy założył je również
Ptolemeusz I, czy, około 280 r. p.n.e., Ptolemeusz II Filadelfos.
Muzeum było finansowaną przez kolejnych
władców z dynastii Ptolemeuszów wspólnotą uczonych, którzy zajmowali się
badaniami matematycznymi i przyrodniczymi, zwłaszcza w zakresie astronomii,
mechaniki, pneumatyki, optyki, fizjologii i geografii. (Prowadzono również
systematyczne badania nad literaturą, co wykracza jednak poza zakres tematyczny
tej książki.) W Aleksandrii w okresie hellenistycznym nie było natomiast
filozofów. Co ciekawe, uczeni aleksandryjscy nie tylko nie podejmowali zagadnień
z zakresu etyki czy logiki (jako teorii wiedzy), nie interesowała ich też teoria
świata jako całości. Nawet nie próbowali stworzyć systemu fizyki konkurencyjnego
względem Arystotelesowskiego. Pochłaniały ich zagadnienia cząstkowe, konkretne.
Zdaje się, że niektórzy pracowali jako konstruktorzy machin wojennych i innych
urządzeń technicznych – choć nic nie wiemy o tym, aby były one produkowane na
większą skalę. Ptolemeusze mogli finansować uczonych po prostu dla dodania sobie
splendoru.
1.
Elementy Euklidesa
U zarania nauki aleksandryjskiej Euklides – o
którym jako o człowieku nic nie wiemy – opublikował Stoicheion,
czyli Elementy. W Komentarzu do I księgi Elementów,
jaki w V w. napisał neoplatonik Proklos, czytamy:
Niewiele młodszy od tych [uczniów Platona]
jest Euklides, który połączył razem elementy, gromadząc i porządkując wiele z
twierdzeń Eudoksosa, dopracowując wiele z twierdzeń Teajteta, a także w
nieobalalny sposób wykazując rzeczy, które zostały mniej skrupulatnie
dowiedzione przez jego poprzedników. Ten człowiek żył w czasach pierwszego
Ptolemeusza, gdyż Archimedes, który żył zaraz po pierwszym Ptolemeuszu, robi o
Euklidesie wzmiankę. A następnie powiadają, że Ptolemeusz spytał go pewnego
razu, czy istnieje krótsza droga do studiowania geometrii niż
Elementy,
na co odparł, że nie ma królewskiej drogi do geometrii. Jest on zatem młodszy
niż krąg Platona, a starszy niż Archimedes i Eratostenes, ci bowiem, jak to
Eratostenes gdzieś powiada, byli sobie współcześni. Jeśli o cel chodzi, to był
platonikiem, sympatyzującym z tą filozofią i stąd zakończył całe
Elementy
konstrukcją tak zwanych brył platońskich.
Pisząc po upływie ośmiu stuleci Proklos
nie dysponuje już precyzyjnymi danymi i nie jest w stanie krytycznie odróżnić
faktów od narosłych w ciągu wieków legend. Inne źródła jeszcze mniej zasługują
na zaufanie. Skoro Euklides korzystał z prac uczniów Platona, to jest
prawdopodobne, że nauki pobierał w Akademii. Parę źródeł wiąże go z Aleksandrią,
żadne jednak nie podaje, jak długo przebywał w tym mieście i w jaki sposób był z
nim związany.
Zasadniczy problem leży w tym, że poszczególne
księgi Elementów
dość wyraźnie różnią się stylem, a ponadto występują między nimi pewne
niezgodności i niekonsekwencje. Może to świadczyć albo o tym, iż całość jest
kompilacją dzieł wcześniejszych geometrów, albo że jest to dzieło wielu autorów,
pracujących być może pod kierunkiem człowieka o imieniu Euklides.
To, co wiadomo o historii helleńskiej geometrii przed Euklidesem, omówiliśmy w zarysie w
§§ II.12 i V.4. Wspominaliśmy tam, że autorstwo niektórych ksiąg Elementów –
lub zasadniczy wkład w wyłożone tam treści – przypisuje się Hippokratesowi z Chios (księgi
I i II), Eudoksosowi z Knidos (V), Archytasowi z Tarentu (VIII, może też
fragmenty VII) i Teajtetowi z Aten (X i XIII).
Przy wszystkich niejasnościach co do autorstwa
tekstu oraz przedstawionych w nim twierdzeń i dowodów, oraz pewnych braków
kompozycyjnych, jest to jedno z najdoskonalszych dzieł, jakie stworzyła
ludzkość. Dość powiedzieć, że było wykorzystywane jako podręcznik do połowy
XIX w. i dopiero wtedy zdołano udoskonalić przedstawiony w
Elementach system (a także sformułowano alternatywne systemy geometryczne).
Tekst otwierają 23 definicje, m.in.:
Definicja 1. Punkt jest tym, co nie ma części.
Definicja 2. Linia jest długością bez szerokości.
Definicja 3. Końce linii są punktami.
Definicja 4. Linia prosta jest linią leżącą jednostajnie na swych punktach.
Definicja 5. Powierzchnia jest tym, co ma jedynie długość i szerokość.
Definicja 6. Krawędzie powierzchni są liniami.
Definicja 7. Płaszczyzna jest powierzchnią leżącą jednostajnie na swych liniach.
Definicja 10. Kiedy linia prosta stojąca na linii prostej tworzy przyległe kąty
równe sobie, to każdy z równych kątów jest prosty, a linia prosta stojąca na tej
drugiej nazywa się prostopadłą do niej.
Definicja 23. Równoległe linie proste to
linie proste, które, leżąc na tej samej płaszczyźnie i przedłużone
nieograniczenie w obie strony, nie przecinają się po żadnej ze stron.
Po czym następują słynne postulaty:
Postulat 1. [Można] narysować linię prostą z dowolnego punktu do dowolnego punktu.
Postulat 2. [Można] przedłużyć skończoną linię prostą w sposób ciągły w linię prostą.
Postulat 3. [Można] opisać okrąg wokół dowolnego środka i o dowolnym promieniu.
Postulat 4. Że wszystkie kąty proste są sobie równe.
Postulat 5. Że jeśli linia prosta, przecinająca dwie proste, tworzy [z nimi] po jednej stronie kąty wewnętrzne
mniejsze od dwóch kątów prostych, to te dwie proste, jeśli przedłuży się je
nieograniczenie, przetną się po tej stronie, po której znajdują się kąty
mniejsze od dwóch kątów prostych.
I jeszcze pięć pojęć powszechnych:
Pojęcie powszechne 1. Rzeczy równe pewnej rzeczy są równe między sobą.
Pojęcie powszechne 2. Jeśli równe dodamy do równych, to całości są równe.
Pojęcie powszechne 3. Jeśli równe odejmiemy od równych, to pozostałości są równe.
Pojęcie powszechne 4. Rzeczy pokrywające się ze sobą są sobie równe.
Pojęcie powszechne 5. Całość jest mniejsza niż część.
Dziś podane przez Euklidesa definicje uznaje
się w matematyce zarówno za niepoprawne, jak i za zbędne. Natomiast jego
postulaty nazywamy aksjomatami
– i one koncentrują na sobie naszą uwagę. W sformułowaniu Euklidesa postulaty od
1 do 3 orzekają, że pewne konstrukcje geometryczne są wykonalne (dziś w miejsce
1 wstawilibyśmy raczej: „przez dowolne dwa różne punkty przechodzi dokładnie
jedna prosta” – Euklides zakłada, że ta prosta jest jedna, ale wyraźnie tego nie
zaznacza). Postulaty 4 i 5 stwierdzają, iż te konstrukcje mają takie a takie
własności.
Resztę tekstu wypełniają twierdzenia
geometryczne oraz ich dowody. Całością rządzi idea następująca. Są twierdzenia
geometryczne, co do których zrazu nie wiemy, czy są prawdziwe, np. „trzy
dwusieczne kątów dowolnego trójkąta przecinają się w jednym punkcie”. Ale to, że
„przez dwa punkty przechodzi dokładnie jedna prosta”, jest oczywiste dla każdego
człowieka (dorosłego i zdrowego na umyśle). Jeśli przesłanki są prawdziwe, to
wynikanie logiczne gwarantuje prawdziwość wniosku. A zatem jednych twierdzeń
można, na podstawie innych twierdzeń, dowodzić.
W rezultacie narodził się program znalezienia
twierdzeń, których prawdziwość byłaby oczywista, czyli aksjomatów, z których
wynikałyby wszystkie inne twierdzenia, jakie tylko dałoby się wymyślić. Ten
program w Elementach
został zrealizowany w sposób niemal doskonały: podane tam aksjomaty są logicznie
niezależne (żaden nie wynika logicznie z pozostałych) i wystarczają do
dowiedzenia (choć, jak stwierdzono w XIX w., przy pewnych milcząco przyjętych
założeniach) wszystkich twierdzeń geometrii zwanej dziś „euklidesową”. Żadnych
przykładów nie będziemy tu omawiać, są to bowiem trudne kwestie techniczne.
Przyda się natomiast krótka informacja o zawartości dzieła.
Księgi od I do VI dotyczą geometrii na
płaszczyźnie. I i II poświęcone są własnościom trójkątów, równoległoboków,
prostokątów, kwadratów. Przedmiotem III i IV są własności koła i problemy z tym
związane. W V traktuje o proporcjach, zarówno współmiernych, jak i
niewspółmiernych; jej wyniki są stosowane w księdze VI.
Księgi od VII do IX zawierają teorię
liczb (w księdze VIII sporo jest zbędnych powtórzeń, a nawet błędów, co zdaje
się świadczyć o tym, że przenikliwość zawodziła autora tam, gdzie nie miał do
dyspozycji dobrych źródeł). Księga X dotyczy liczb niewymiernych.
Księgi od XI do XIII dają wykład
geometrii trójwymiarowej. Twierdzenia budowane są przez analogię z geometrią
dwuwymiarową. W księdze XII stosując metodę wyczerpywania Euklides wykazuje
m.in., że tak jak stosunek powierzchni kół jest równy stosunkowi kwadratów ich
średnic, tak stosunek sześcianów średnic określa stosunek objętości kul. Księga
XIII dotyczy własności brył foremnych.
Ocalały jeszcze cztery teksty
przypisywane Euklidesowi; parę innych, wymienianych przez starożytnych autorów,
zaginęło.
Podział figur zachował się
jedynie częściowo, do tego w przekładzie arabskim. Dotyczy dzielenia figur
płaskich na równe części lub na części o danych proporcjach.
Dane zawierają 94
twierdzenia na temat własności figur, które mogą zostać wydedukowane, gdy
określone zostały pewne inne ich własności.
Phaenomena
(Zjawiska) to tekst z zakresu elementarnej astronomii, w którym wykorzystuje się
zasady geometrii sferycznej. Nie ma w nim żadnej teorii ruchów planet i gwiazd.
Punktem wyjścia jest twierdzenie, że gwiazdy poruszają się ruchami jednostajnymi
po równoległych okręgach, których wspólny środek stanowi „pewna gwiazda między
Niedźwiedzicami”, tak że odległości między nimi pozostają stałe. Głównym celem
rozważań jest określenie chwili, w której poszczególne gwiazdy wschodzą i
zachodzą.
Optyka to pierwsze
znane dzieło o perspektywie, dotyczące wielkości i kształtów rzeczy widzianych z
różnych odległości pod różnymi kątami.
2. Biologia i medycyna Herofilosa z Chalkedonu i Erasistratosa z Keos
Prace autorów Korpusu Hippokratejskiego
kontynuowali Diokles z Karystos, Praksagoras z Kos, Chryzyp z Knidos i inni. Na
jakościowo nowy poziom badania nad budową ciała ludzkiego wprowadzili dwaj
uczeni z Aleksandrii: Herofilos z Chalkedonu (ok. 335-280 p.n.e.) i Erasistratos
z Keos (ok. 310-250 p.n.e.). Nie ocalało żadne z ich dzieł, to, co o nich wiemy,
pochodzi z pism Celsusa (I w.), Rufusa z Efezu (koniec I w.), Soranosa z Efezu
(początek II w.), a przede wszystkim Galena z Pergamonu (II w., zob. § XVI.3).
Celsus w De medicina i Tertulian w O duszy
donoszą, że królowie aleksandryjscy darowywali Herofilosowi i Erasistratosowi
skazanych na śmierć przestępców, oni zaś rozcinali ich żywcem aby zaobserwować
działanie narządów wewnętrznych. Mieli nadzieję, że dzięki tym badaniom znajdą
sposoby leczenia wielu chorób. Ale większość z dokonanych przez nich odkryć
pochodziła z sekcji zwłok – co w innych czasach i miejscach było zakazane przez
prawo.
Herofilos badał budowę mózgu. Stwierdził
– wbrew opiniom większości filozofów – że stanowi on centrum układu nerwowego.
Rozróżnił nerwy sensoryczne i motoryczne. Opisał budowę oka (od niego pochodzi
termin „siatkówka”). Studiował budowę serca, wątroby, dwunastnicy i innych
narządów wewnętrznych. Odkrył jajniki i porównał je z jądrami u mężczyzn.
Jeśli o praktykę medyczną chodzi, to jego
główny wkład polegał na rozwinięciu metod diagnostycznych opartych na mierzeniu
pulsu. Źródło pulsu lokował nie – jak czynili to jego poprzednicy – w tętnicach
ale w sercu. Wniósł też wkład do dietetyki i farmakologii.
Trudno często, jeśli chodzi o odkrycia w
zakresie anatomii, odróżnić dorobek Herofilosa od dokonań młodszego od niego
Erasistratosa. Zapewne wiele badań przeprowadzili wspólnie. Temu drugiemu
natomiast źródła przypisują rozwijanie mechanicznej – opartej na fizyce
Arystotelesa, z domieszką pomysłów Stratona – teorii funkcjonowania organizmu.
Podczas gdy Arystoteles uważał (zob.
V.10), że przetwarzanie pokarmu polega na jego gotowaniu, to Erasistratos, bodaj
na podstawie zaobserwowanych podczas wiwisekcji ruchów narządów wewnętrznych,
głosił, że pokarm, przepchnięty przez ruchy przełyku do żołądka jest tam
rozdrabniany wskutek jego skurczów. Następnie przeciśnięty przez ścianki żołądka
dostaje się do naczyń krwionośnych. Z tkanek usuwane są stale zużyte resztki, a
że natura nie znosi próżni, to powoduje to wsysanie rozpuszczonego w krwi
pokarmu przez ścianki żył w opróżnione miejsca. Pokarm przekazywany jest więc do
tkanek przez żyły. Natomiast tętnicami rozchodzi się po organizmie powietrze.
Erasistratos był pierwszym, być może,
badaczem, który poprawnie zrozumiał funkcjonowanie zastawek w sercu. Twierdził,
że działa ono analogicznie jak pompa – ale tłocząca w tętnicach, należących do
dużego krwiobiegu, nie krew, a powietrze. Krew wpływa żyłami do serca, a
następnie wtłaczana jest przez nie do tętnicy płucnej, aby dostarczyć płucom
pokarmu. Przy rozkurczu za pośrednictwem żył płucnych do serca wciągane jest
powietrze, które przy kolejnym skurczu wtłaczane jest do tętnic rozchodzących
się po całym ciele. Uczony aleksandryjski nie odkrył więc krwiobiegu (dokonał
tego William Harvey w 1628 r.), choć pojawia się u niego wyobrażenie
niedostrzegalnych naczyń krwionośnych, zwanych dziś włosowatymi. Postulował ich
istnienie gdyż wiedział, rzecz jasna, iż po przecięciu tętnicy wypływa z niej
krew. Tłumaczył to tak, że gdy powietrze szybko uchodzi, lęk przed próżnią
powoduje, iż do tętnic przez wspomniane naczynia szybko zasysana jest krew z
żył. Przez naczynia włosowate krew przelewa się też do tętnic wtedy, gdy jest
jej zbyt wiele – co powoduje niektóre choroby, które można leczyć przez
upuszczanie krwi.
Ważne były jego prace nad budową układu
nerwowego. Podejrzewał, że nerwy rozgałęziają się na niewidoczne gołym okiem
żyłki, obecne w każdej tkance. Nerwami z mózgu po całym ciele miało rozchodzić
się powietrze w jakiejś subtelnej formie. Znamy tę koncepcję z prac Galena, że
jednak nie potrafimy oddzielić pomysłów Erasistratosa od idei uczonego z
Pergamonu, omówimy krótko ten pogląd w § XVI.3.
Zdaje się, że Herofilos i Erasistratos
nie znaleźli następców. Chyba nie tylko nie dokonywano po nich wiwisekcji, ale z
niejasnych powodów także sekcji zwłok. Później rozcinanie w celach badawczych
martwych ludzkich ciał zostało zakazane przez prawo. (To samo prawo nie
zakazywało jednak ani walk gladiatorów, ani stosowania tortur w śledztwie.)
Działały w ciągu kolejnych stuleci szkoły lekarskie, w których stopniowo
rozwijano techniki leczenia niektórych chorób. Ale na postęp w badaniach
anatomicznych trzeba było po śmierci obu wielkich uczonych z Aleksandrii
poczekać cztery stulecia.
3. Wynalazki Ktesibiosa z Aleksandrii i Filona z Bizancjum
Ktesibios z Aleksandrii (ok.285-ok.222 p.n.e.)
podobno był najpierw, podobnie jak jego ojciec, fryzjerem. Wynalazki, jakich
dokonał, wyniosły go – choć nie jest to pewne – do rangi pierwszego scholarchy
Muzeum. Wszystkie jego dzieła, a przede wszystkim słynne
O pneumatyce, zaginęły. Mamy natomiast wzmianki o konstruowanych przez Ktesibiosa urządzeniach
w O architekturze Witruwiusza (13 p.n.e.), a także w pismach Herona z Aleksandrii (I w. n.e.) i
innych starożytnych autorów.
Przypisuje mu się skonstruowanie pompy
wodnej składającej się z dwóch cylindrów, w których poruszały się tłoki, a
przepływ wody regulowany był przez system zaworów. Witruwiusz twierdzi, że
używano tej pompy do gaszenia pożarów, choć można mieć co do tego wątpliwości.
Konstruował też Ktesibios precyzyjne zegary wodne, w których w zbiorniku, z
którego woda wypływała przez mały otwór, utrzymywał się stały jej poziom, zaś
pływak w naczyniu, gdzie się gromadziła, wskazywał godzinę. Ponieważ godziny w
tamtych czasach powstawały z równego podziału okresu od wschodu do zachodu
słońca, to obok pływaka znajdowała się ruchoma skala, umożliwiająca dostosowanie
wskazań do zmieniającej się w cyklu rocznym długości dnia. Innym jego słynnym
wynalazkiem były organy wodne. Miał też konstruować katapulty, miotające pociski
za pomocą napiętych strun metalowych lub sprężonego powietrza.
Niewiele więcej da się ustalić na temat
wynalazków Ktesibiosa. A przede wszystkim trudno oddzielić jego wkład od wiedzy
i umiejętności rzemieślników, z których z pewnością korzystał.
Witruwiusz w O architekturze wymienia
dwunastu wynalazców maszyn. Na drugim miejscu znajduje się Archytas (zob. §
IV.4), na trzecim Archimedes (zob. § VI.5), na czwartym Ktesibios, a na szóstym Filon.
Filon z Bizancjum (ok. 280-220 p.n.e.) napisał Mechanike syntaxis,
składające się z dziewięciu ksiąg: (I) Wstęp, (II) O dźwigni, (III) O budowie
portu morskiego, (IV) O katapultach, (V) O pneumatyce, (VI) O automatycznym
teatrze, (VII) O budowaniu fortec, (VIII) O obleganiu i bronieniu miast, (IX) O
fortelach. Ocalały księgi IV, V, VII i VIII, ale liczne w tekście odwołania
pozwalają wyrobić sobie opinię o zawartości ksiąg zaginionych. Choć jego badania
nad konstruowaniem maszyn nie wykorzystywały czegoś, co można by nazwać
matematyką stosowaną (co jest codziennością dla inżynierów nam współczesnych),
to problem zbudowania katapulty miotającej pociski dwukrotnie większe niż
miotane przez katapultę już istniejącą, przywiódł go do zagadnienia podwojenia
sześcianu. Filon zredukował je do znajdowania przecięć okręgu z hiperbolą o
prostopadłych asymptotach.
4. Arystarch z Samos o niebie
Arystarch urodził się na wyspie Samos, a nauki
ponoć pobierał w Liceum, pod kierunkiem Stratona z Lampsakos. Obserwował
zaćmienie Słońca w 279 r. p.n.e. (urodził się zapewne jakieś trzydzieści lat
wcześniej). Z jego prac zachowała się jedynie krótka rozprawa
O wielkości i odległości Słońca i Księżyca,
będąca pierwszą w dziejach ludzkości znaną próbą
ustalenia podanych w tytule wartości na podstawie wyników obserwacji. Oto ona:
Hipotezy:
1. Że Księżyc otrzymuje swe światło od Słońca.
2. Że Ziemia pozostaje w relacji punktu i środka do sfery, na której porusza się Księżyc.
3. Że kiedy widzimy półksiężyc, wielkie koło dzielące Księżyc na części ciemną i jasną jest usytuowane w kierunku
naszego oka.
4. Że kiedy widzimy półksiężyc, jego odległość od Słońca jest równa kątowi
prostemu pomniejszonemu o jedną trzydziestą tego kąta.
5. Że szerokość cienia Ziemi wynosi dwa Księżyce.
6. Że Księżyc zajmuje jedną piętnastą część znaku zodiaku.
Możemy teraz dowieść następujących twierdzeń:
A. Odległość Słońca od Ziemi jest większa
niż osiemnaście razy, a mniejsza niż dwadzieścia razy, od odległości Księżyca od
Ziemi; to wynika z hipotezy o półksiężycu.
B. Średnica Słońca pozostaje w tym samym stosunku do średnicy Księżyca.
C. Stosunek średnicy Słońca do średnicy Ziemi wynosi więcej niż 19 do 3,
a mniej niż 43 do 6; to wynika z odkrytego
właśnie stosunku między odległościami, hipotezy o cieniu i hipotezy, że Księżyc
zajmuje jedną piętnastą części znaku zodiaku.
Tekst ten wymaga komentarza.
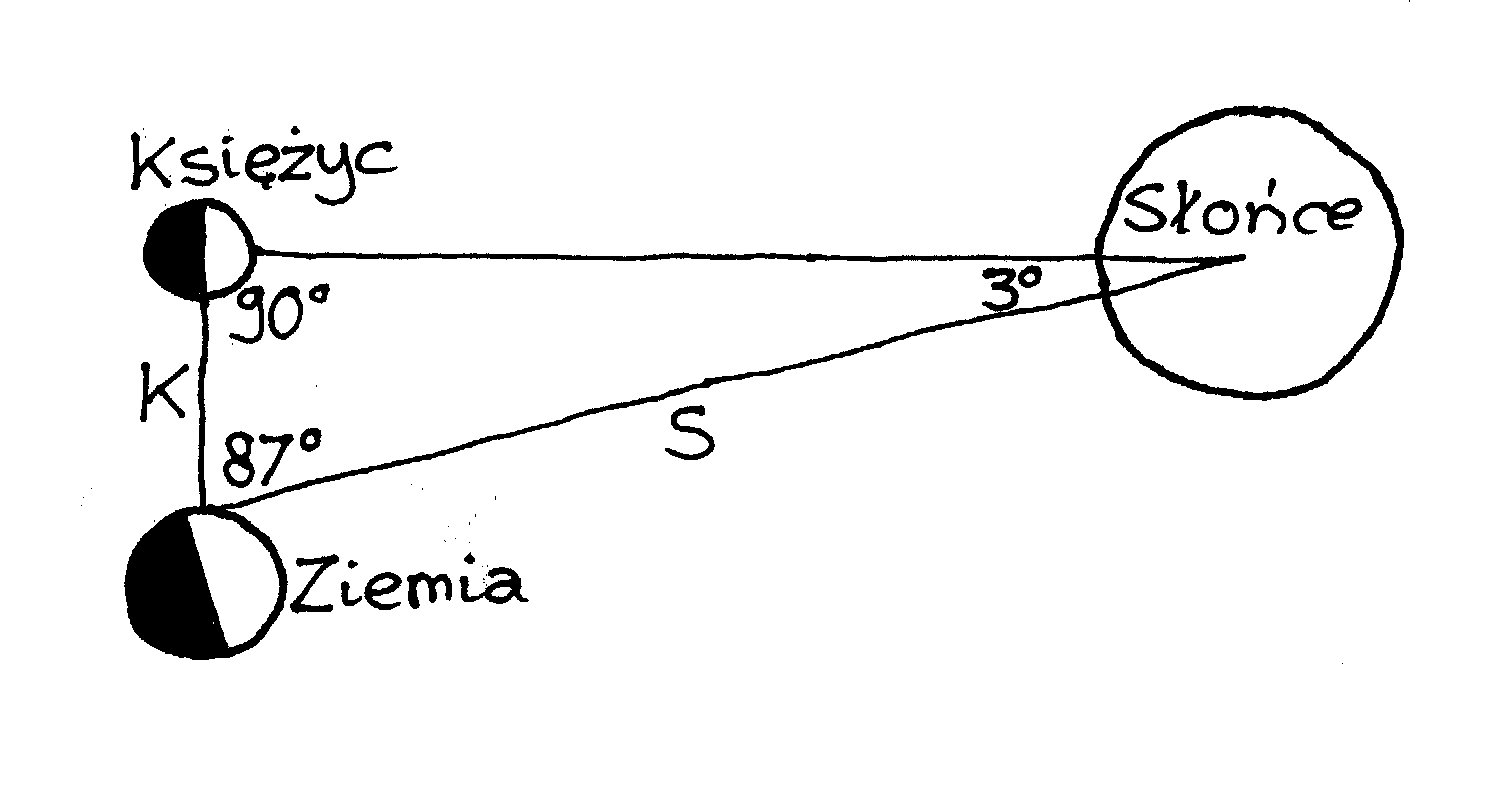 Arystarch zakłada (hipoteza 2), że odległość
Księżyca do Ziemi pozostaje stała (co już w tym czasie, z uwagi na mierzalną za
pomocą prostych przyrządów zmianę średnicy widocznej tarczy Księżyca, trzeba
było traktować jako przybliżenie). Hipoteza 3, wynikająca faktycznie z 1 i
obiegowego w tym czasie założenia, że Księżyc jest kulą, głosi, że kiedy widać
połowę tarczy Księżyca, to linia łącząca Ziemię z Księżycem leży pod kątem
prostym do linii łączącej Księżyc ze Słońcem. Hipoteza 4 nie jest z naszego
punktu widzenia hipotezą, ale sprawozdaniem z wyników pomiarów. Głosi ona, że
kiedy widać na niebie jednocześnie półksiężyc i Słońce, dzieli je odległość
kątowa równa 870.
Wobec tego stosunek odległości Słońce-Ziemia S do odległości Słońce-Księżyc K
jest równa tangensowi 870,
ten zaś wynosi ok. 19.
Arystarch zakłada (hipoteza 2), że odległość
Księżyca do Ziemi pozostaje stała (co już w tym czasie, z uwagi na mierzalną za
pomocą prostych przyrządów zmianę średnicy widocznej tarczy Księżyca, trzeba
było traktować jako przybliżenie). Hipoteza 3, wynikająca faktycznie z 1 i
obiegowego w tym czasie założenia, że Księżyc jest kulą, głosi, że kiedy widać
połowę tarczy Księżyca, to linia łącząca Ziemię z Księżycem leży pod kątem
prostym do linii łączącej Księżyc ze Słońcem. Hipoteza 4 nie jest z naszego
punktu widzenia hipotezą, ale sprawozdaniem z wyników pomiarów. Głosi ona, że
kiedy widać na niebie jednocześnie półksiężyc i Słońce, dzieli je odległość
kątowa równa 870.
Wobec tego stosunek odległości Słońce-Ziemia S do odległości Słońce-Księżyc K
jest równa tangensowi 870,
ten zaś wynosi ok. 19.
Dziś przyjmujemy, że stosunek tych odległości
wynosi ok. 390, a zatem Arystarch podał wartość dwudziestokrotnie mniejszą. Ale
metoda, jaką się posłużył, była poprawna! Po prostu gołym okiem nie da się
dokładnie ocenić momentu, kiedy widzimy połowę tarczy Księżyca, a wartość
tangensa gwałtownie rośnie przy zbliżaniu się do 900.
Poprawna wartość kąta wynosiłaby 89052',
tak więc błąd pomiarowy – w tym czasie nie do uniknięcia – rzędu dwa i pół
stopnia dał wspomnianą różnicę wyników. Tak czy inaczej wykazanie, że Słońce
znajduje się o wiele dalej niż Księżyc, było wielkim osiągnięciem. Osiągnięciem
było też wykazanie, że Księżyc jest o wiele mniejszy od Słońca (choć stosunek
średnic od 18 do 20 jest równie – i z tego samego powodu – błędny, jak podany
przez Arystarcha stosunek odległości tych ciał).
Hipotezy 5 i 6 relacjonują wyniki pomiarów. W
6 jest zdumiewający błąd: widoczna średnica tarczy Księżyca wynosi ok. 30', a
zatem zajmuje on czterokrotnie mniejszą część znaku Zodiaku niż podana przez
Arystarcha. Jak tę pomyłkę wytłumaczyć, nikt dziś nie wie. (Warto zaznaczyć, że
w pisanym nieco później tekście Archimedesa znajdujemy wielkość poprawną:
„Arystarch odkrył, że Słońce zajmuje 1/720 część koła Zodiaku” [O
liczeniu piasku,
uwaga do założenia 4]).
Następnie Arystarch przystąpił do
wyznaczenia odległości Ziemi od obu jej kosmicznych sąsiadów w skali
bezwzględnej. Wykorzystał w tym celu zjawisko całkowitego zaćmienia Księżyca –
co do którego co najmniej wiek wcześniej ustalono, że polega ono na tym, iż
Księżyc wchodzi w cień Ziemi (zob. rozdz. V.5). Otóż czas, w trakcie którego
cień Ziemi nasuwa się na tarczę Księżyca w trakcie jego całkowitego zaćmienia,
jest dwukrotnie krótszy (dziś poprawilibyśmy Arystarcha: dwa i pół raza krótszy)
niż czas, w jakim Księżyc znajduje się cały w cieniu. Stąd – i ze spostrzeżenia,
że ruch Księżyca jest w dobrym przybliżeniu jednostajny – wynika, że średnica
Księżyca d jest dwukrotnie mniejsza niż szerokość cienia rzucanego przez Ziemię
w miejscu, gdzie on się znajduje (hipoteza 5).
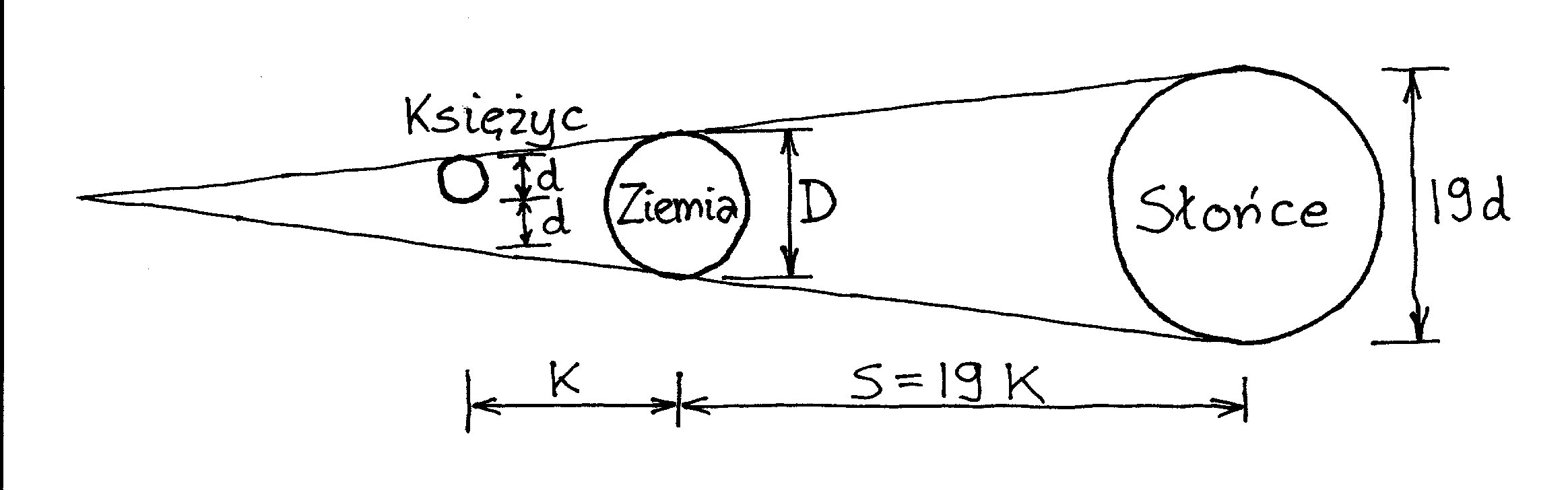 Jeśli podstawimy, zgodnie z poprzednimi
ustaleniami, że K ≈ 19 S, to z porównania trójkątów i po kilku trywialnych
przekształceniach otrzymujemy K ≈ 10 D, tzn. Księżyc odległy jest od Ziemi o ok.
10 jej średnic (dziś przyjmujemy K ≈ 30 D). Wobec tego S ≈ 190 D, zaś stosunek
średnicy Słońca do średnicy Ziemi wynosi ok. 6 2/3. (A zatem Słońce jest o wiele
większe od Ziemi. Pamiętajmy, iż dwieście lat wcześniej oskarżano Anaksagorasa o
bezbożność m.in. dlatego, że twierdził, iż Słońce jest większe od Peloponezu.)
Czy Arystarch znał choćby w przybliżeniu średnicę Ziemi, nie wiadomo. (Zob.
poniżej rozdział o Eratostenesie).
Jeśli podstawimy, zgodnie z poprzednimi
ustaleniami, że K ≈ 19 S, to z porównania trójkątów i po kilku trywialnych
przekształceniach otrzymujemy K ≈ 10 D, tzn. Księżyc odległy jest od Ziemi o ok.
10 jej średnic (dziś przyjmujemy K ≈ 30 D). Wobec tego S ≈ 190 D, zaś stosunek
średnicy Słońca do średnicy Ziemi wynosi ok. 6 2/3. (A zatem Słońce jest o wiele
większe od Ziemi. Pamiętajmy, iż dwieście lat wcześniej oskarżano Anaksagorasa o
bezbożność m.in. dlatego, że twierdził, iż Słońce jest większe od Peloponezu.)
Czy Arystarch znał choćby w przybliżeniu średnicę Ziemi, nie wiadomo. (Zob.
poniżej rozdział o Eratostenesie).
W rozprawie O wielkości i odległości Słońca i Księżyca
nie ma ani słowa o tym, które z ciał niebieskich są w ruchu, a które z nich
ewentualnie tkwi nieruchomo w środku świata – a zatem ani słowa o teorii, która
do dziś rozsławia imię Arystarcha. Znamy ją z krótkiej uwagi, jaką wkrótce
później uczynił Archimedes:
Ty, królu
Gelonie, zdajesz sobie sprawę z tego, że wszechświatem większość astronomów
nazywa sferę, której środkiem jest środek Ziemi, a jej promień jest równy linii
poprowadzonej od środka Słońca do środka Ziemi. Taki powszechnie panujący pogląd
przekazali ci astronomowie. Ale Arystarch z Samos ogłosił dzieło zawierające
pewne hipotezy, z których wynika, jako konsekwencja poczynionych założeń, że
wszechświat jest o wiele większy niż wszechświat przed chwilą wspomniany.
Zgodnie z jego hipotezami gwiazdy stałe i Słońce pozostają nieruchome, Ziemia
krąży po obwodzie koła wokół Słońca znajdującego się w jego środku, a sfera
gwiazd stałych, mająca również za środek Słońce, jest tak wielka, że koło, po
którym jak on przypuszcza krąży Ziemia, ma się do odległości gwiazd stałych tak,
jak środek sfery ma się do jej powierzchni. Jest to, jak łatwo zauważyć,
niemożliwe, gdyż środek sfery w ogóle nie ma wielkości i nie sposób sobie
wyobrazić, w jakim stosunku miałby on pozostawać do powierzchni sfery. Arystarch
z pewnością rozumiał to więc następująco. Ponieważ, jak sądzimy, Ziemia jest
środkiem świata, zatem stosunek jej rozmiarów do tego, co nazywamy
wszechświatem, jest równy stosunkowi, w jakim sfera zawierająca okrąg, po którym
zgodnie z jego przypuszczeniem krąży Ziemia, ma się do sfery gwiazd stałych. [O
liczeniu piasku
I]
Nie jest to prezentacja teorii
Arystarcha, nie ma w niej np. ani słowa o tym, że Ziemia okrąża Słońce w ciągu
jednego roku. A przede wszystkim nie ma wzmianki o drugiej istotnej hipotezie:
Ziemia wiruje ruchem dobowym wokół własnej osi – choć wynika ona w oczywisty
sposób ze wzmianki o nieruchomości sfery gwiazd. Wyraźnie o obu hipotezach pisał
– ale ponad trzy wieki później – Plutarch:
Kleantes
uważał, że Hellenowie powinni o bezbożność oskarżyć Arystarcha z Samos, jako że
poruszył z miejsca ognisko domowe świata, ponieważ usiłował „ocalić zjawiska”,
przyjmując, że niebo jest nieruchome, a ziemia wiruje po ekliptyce, a
jednocześnie obraca się dokoła własnej osi. [Plutarch,
O obliczu widniejącym na tarczy Księżyca
923A]
Możemy jedynie spekulować, co przywiodło
Arystarcha do sformułowania takiej teorii. Pogląd, że Ziemia wiruje ruchem
dobowym wokół własnej osi, natomiast sfera gwiazd stałych pozostaje nieruchoma,
głosił już ok. 350 r. p.n.e. uczeń Platona, Heraklides z Pontu. Twierdził też,
być może, iż Wenus krąży wokół Słońca, które wraz z nią obiega ruchem rocznym
nieruchomą Ziemię. Jeśli dodamy do tego omówione powyżej wyniki obliczeń,
zgodnie w którymi Słońce jest od Ziemi o wiele większe, to może się na tej
podstawie nasunąć myśl, że to Słońce jest nieruchome, a Ziemia, wraz z Wenus,
krąży wokół niego. Problem w tym, że dostępne źródła nic nie mówią o tym, jak,
według Arystarcha, miałyby się poruszać Księżyc, Merkury, Wenus, Mars, Jowisz i
Saturn. (Tak więc gdy Kopernik przeczytał, w pierwszych latach XVI w., o
koncepcji Arystarcha, tak czy inaczej musiał prawie całą swą teorię wymyślić
sam).
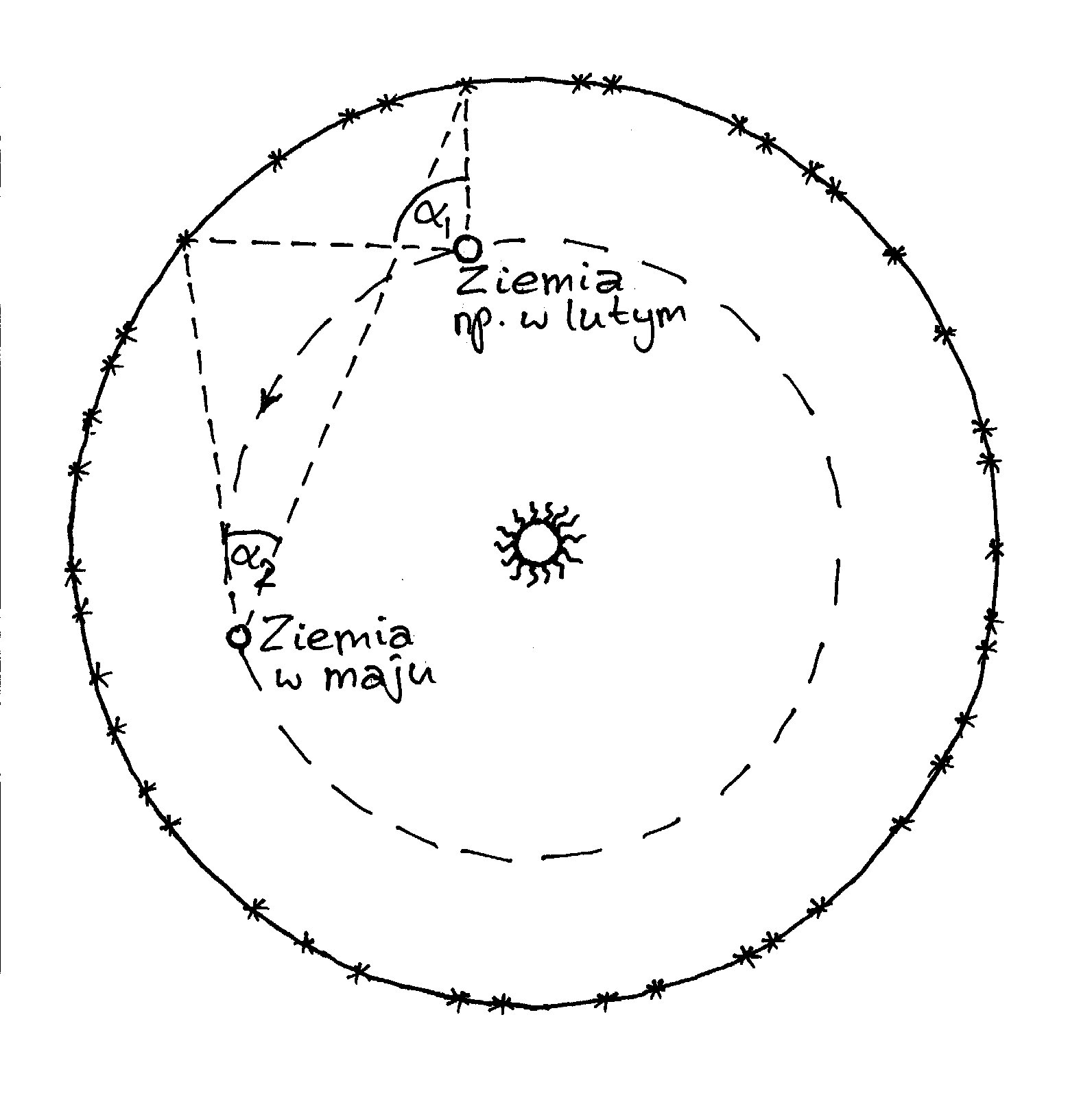 Cytowany
fragment z Archimedesa dotyczył innego niż ruch Ziemi zagadnienia – a był to
koronny zarzut, jaki przeciw heliocentryzmowi formułowano do początków XVII w.
Otóż gdyby Ziemia obiegała nieruchome Słońce, to w cyklu rocznym musiałaby
zbliżać się i oddalać od poszczególnych gwiazd. A wobec tego obserwowalibyśmy
zjawisko zwane paralaksą gwiezdną:
kąty, pod jakimi widać na niebie gwiazdy – zwłaszcza te leżące w pobliżu
płaszczyzny ekliptyki – w cyklu rocznym na przemian rosłyby i malały.
Przedstawmy to na rysunku, zaznaczając domniemane położenia Ziemi w jej wędrówce
wokół Słońca w odstępie 3 miesięcy.
Cytowany
fragment z Archimedesa dotyczył innego niż ruch Ziemi zagadnienia – a był to
koronny zarzut, jaki przeciw heliocentryzmowi formułowano do początków XVII w.
Otóż gdyby Ziemia obiegała nieruchome Słońce, to w cyklu rocznym musiałaby
zbliżać się i oddalać od poszczególnych gwiazd. A wobec tego obserwowalibyśmy
zjawisko zwane paralaksą gwiezdną:
kąty, pod jakimi widać na niebie gwiazdy – zwłaszcza te leżące w pobliżu
płaszczyzny ekliptyki – w cyklu rocznym na przemian rosłyby i malały.
Przedstawmy to na rysunku, zaznaczając domniemane położenia Ziemi w jej wędrówce
wokół Słońca w odstępie 3 miesięcy.
Takiego zjawiska nie obserwujemy – co
zdaje się dowodzić nieruchomości Ziemi. Arystarch odpowiadał na to – jak wynika
z tekstu Archimedesa – że sfera gwiazd jest tak daleko w porównaniu z rozmiarami
orbity ziemskiej, że paralaksa jest niedostrzegalnie mała. (Dalsza część
przytoczonej uwagi świadczy o tym, że brak paralaksy niepokoił też zwolenników
geocentryzmu: jeśli na powyższym rysunku koło przedstawiające ziemską orbitę
uznamy za obraz samej Ziemi, to również – tym razem w cyklu dobowym – paralaksa
powinna wystąpić. Odpowiedź Archimedesa – promień Ziemi jest niesłychanie mały w
porównaniu z promieniem sfery gwiezdnej – jest dokładnie analogiczna z
odpowiedzią Arystarcha).
Oskarżenia o bezbożność, wspomniane przez
Plutarcha, były jednym z powodów, dla których teoria heliocentryczna nie
znalazła uznania. Padały też rozmaite argumenty przeciwko twierdzeniu o ruchu
Ziemi, które znamy w wersji przedstawionej przez Ptolemeusza w II w. n.e.
(omówione zostaną w § XV.2).
Jedynym znanym nam uczonym, który opowiedział
się po stronie Arystarcha, był Seleukos z Seleukei, babiloński uczony żyjący
zapewne w II w. p.n.e. Plutarch wspomina, że podczas gdy Arystarch stawiał
jedynie hipotezę ruchu Ziemi, to Seleukos również ją udowadniał [Platonicae
quaestiones
VIII,1]. Ale jak udowadniał i co konkretnie
twierdził o ruchach ciał niebieskich, nie wiemy. Uczony znad Tygrysu miał też
powiązać zjawisko przypływów i odpływów mórz z położeniami Księżyca.
5. Archimedes z Syrakuz o liczbie π, polach
figur, objętościach brył, a także o statyce i prawie wyporu
Archimedes urodził się ok. 285 r. p.n.e.
w Syrakuzach. O jego życiu nie wiemy właściwie nic. Znał uczonych
aleksandryjskich Konona z Samos i Eratostenesa z Kyrene. Został zabity w 212 r.
p.n.e. w dniu, w którym po dwóch latach oblężenia wojska rzymskie zdobyły
Syrakuzy.
Był chyba najwybitniejszym z uczonych
starożytnych. Zasłynął jako matematyk i fizyk, a także konstruktor maszyn.
Zachowało się około dziewięciu jego dzieł i nieco fragmentów.
Prace matematyczne Archimedesa oparte
były na systematycznym wykorzystaniu metody wyczerpywania, zwanej niekiedy
„starożytnym całkowaniem”. Znano ją i w niepełnym wymiarze stosowano już
wcześniej, on udoskonalił i uogólnił techniki obliczeniowe.
 Zacznijmy od krótkiego tekstu
O wymierzaniu koła,
który otwiera twierdzenie:
Zacznijmy od krótkiego tekstu
O wymierzaniu koła,
który otwiera twierdzenie:
Powierzchnia dowolnego koła jest równa
[powierzchni] trójkąta prostokątnego, którego jedna z przyprostokątnych równa
jest promieniowi, a druga obwodowi tego koła.
(Co we
współczesnych oznaczeniach prowadzi do wzoru πr2.)
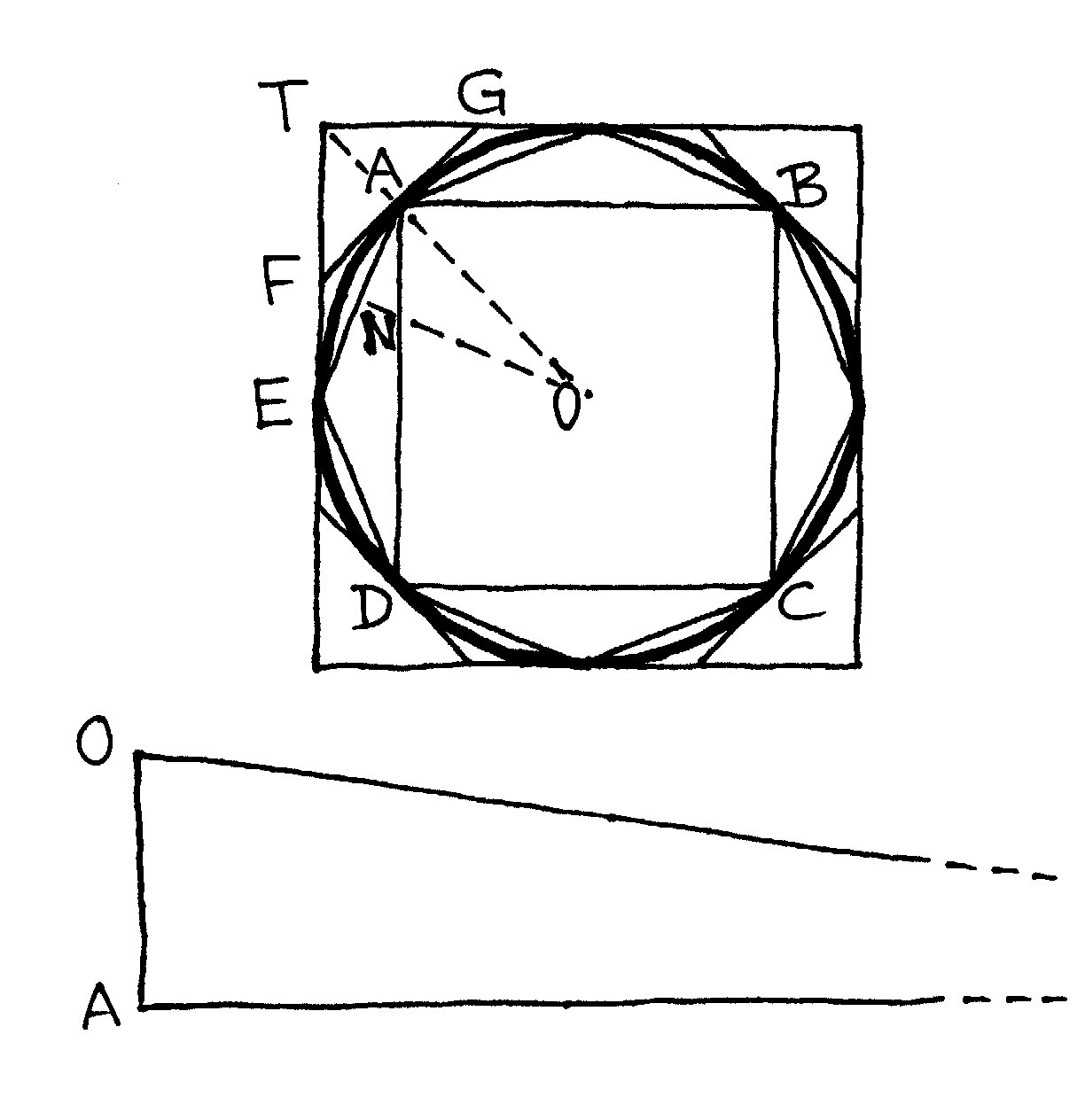
Archimedes konstruuje ciąg wielokątów wpisanych w koło, zaczynając od kwadratu
ABCD, następnie dzieli łuki AB, BC itd. na połowy i umieszcza tam wierzchołki
ośmiokąta AEB... . Jednocześnie opisuje na kole kwadrat o wierzchołku T, po czym
zastępuje go opisanym ośmiobokiem FG... .
Kontynuując tę procedurę otrzymuje ciąg
wielokątów o zwiększającej się liczbie boków i o powierzchniach coraz bardziej
zbliżonych – od dołu i od góry – do powierzchni koła. Sumując pola trójkątów
takich jak ANO (dla dowolnego n-kąta), a także TAG, dowodzi powyższego
twierdzenia metodą redukcji do absurdu.
Następnie, obliczając obwody opisanych na
kole i wpisanych w koło wielokątów, dochodząc do n = 96, ale ukrywając przed
czytelnikiem szereg kroków obliczeniowych, podaje, że
Stosunek obwodu dowolnego koła do jego
średnicy wynosi mniej niż 3 1/7, a więcej niż 3 10/71. [Twierdzenie 3]
Było to pierwsze dokonane z tak dużą
dokładnością wyznaczenie wartości π.
Te wyniki
zostają użyte w najznakomitszej pracy matematycznej Archimedesa,
O kuli i walcu.
Najpierw metodą wyczerpywania – przy użyciu ciągu piramid o podstawie
kwadratowej, ośmiokątnej, szesnastokątnej itd. wpisywanych i opisywanych na
stożku – dowodzi twierdzenia:
Powierzchnia dowolnego stożka
równoramiennego, wyłączając podstawę, jest równa [powierzchni] koła, którego
promień jest średnią proporcjonalną między [tworzącą] stożka a promieniem koła
stanowiącego jego podstawę. [Twierdzenie I.14]
 We współczesnych oznaczeniach jest to równoważne wzorowi πrl.
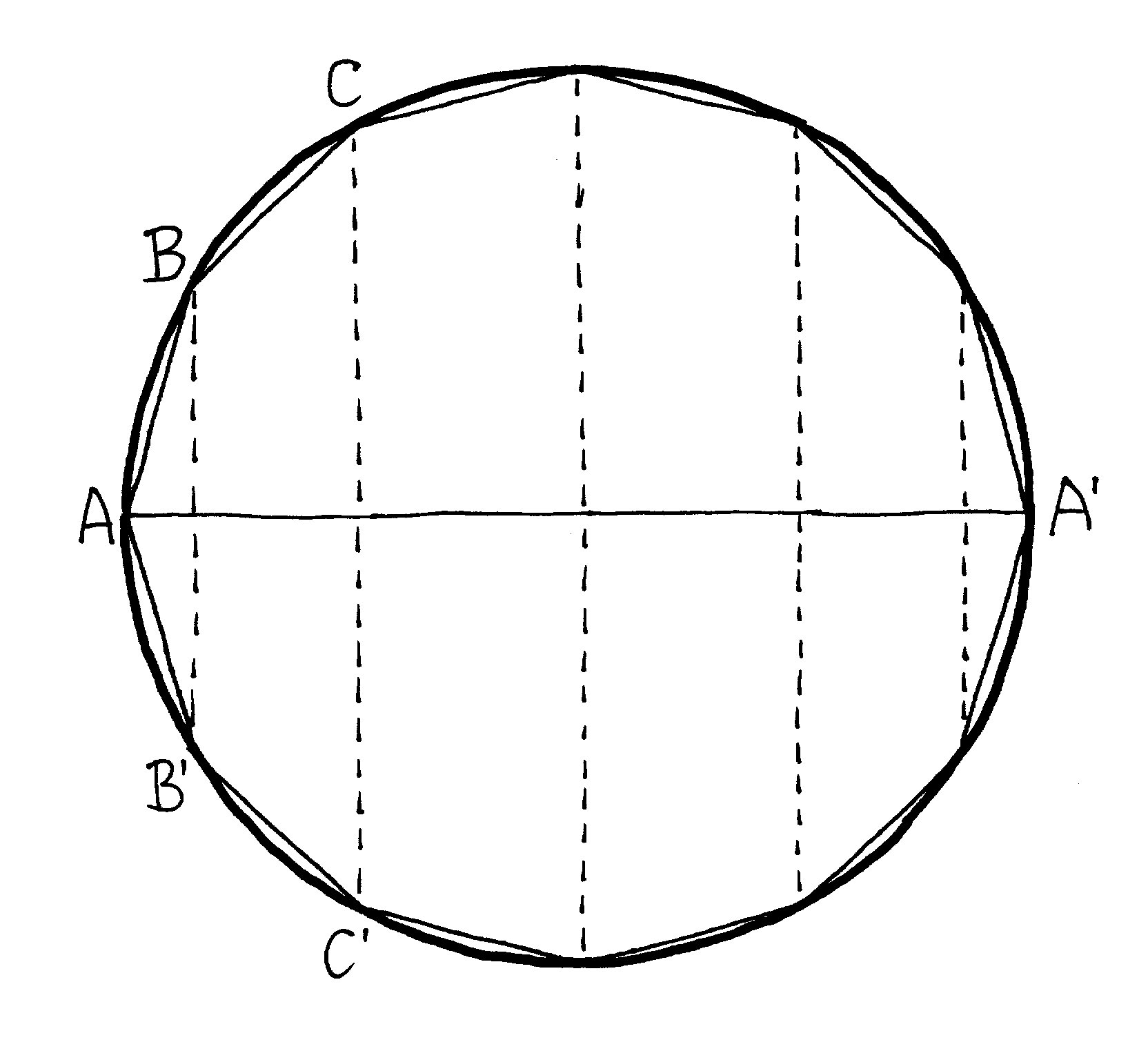
Następnie w koło wielkie sfery Archimedes
wpisuje regularny wielokąt ABC... i obraca go wokół osi AA'.
We współczesnych oznaczeniach jest to równoważne wzorowi πrl.
Następnie w koło wielkie sfery Archimedes
wpisuje regularny wielokąt ABC... i obraca go wokół osi AA'.
Otrzymuje bryłę wpisaną w kulę, której
ściany stanowią kolejno fragmenty powierzchni stożków o podstawach utworzonych
przez obrót odcinków BB', CC' itd. Dowodzi, że dla wielokąta o dowolnej liczbie
boków:
Powierzchnia owej figury wpisanej w sferę
(...), składającej się z części powierzchni stożkowych, jest mniejsza niż
czterokrotność [powierzchni] największego koła w tej sferze. [Twierdzenie I.25]
A następnie, posługując się analogiczną bryłą opisaną na sferze, dowodzi, że:
Powierzchnia figury opisanej tak jak
poprzednio na sferze jest większa niż czterokrotność [powierzchni] największego
koła w tej sferze. [Twierdzenie I.30]
Łącznie prowadzi to rzecz jasna do twierdzenia
Powierzchnia dowolnej sfery jest równa
czterokrotności [powierzchni] największego w niej koła. [Twierdzenie I.33]
We współczesnych oznaczeniach zapiszemy to jako 4πr2.
Równolegle Archimedes dowodził,
analogicznymi metodami, twierdzenia, że objętość stożka równoramiennego jest
równa jednej trzeciej iloczynu pola podstawy i wysokości. Teraz, posługując się
ciągiem brył wykorzystanych w twierdzeniach 25 i 30 dowodzi, że:
[Objętość] dowolnej sfery jest równa
czterokrotności [objętości] stożka, którego podstawa jest taka jak największe
koło tej sfery, a wysokość jest równa promieniowi tej sfery. [Twierdzenie I.34]
We współczesnych oznaczeniach natychmiast prowadzi to do wzoru 4/3 πr3.
Stąd wniosek, który Archimedes miał uznać za swe największe osiągnięcie:
[Objętość] każdego walca, którego
podstawę stanowi największe koło w sferze i którego wysokość jest równa średnicy
tej sfery, wynosi 3/2 objętości sfery, a jego powierzchnia, włączając w to
podstawy, wynosi 3/2 powierzchni sfery.
Księga II dzieła dotyczy powierzchni i
objętości wycinków kuli, otrzymywanych przez przecięcie jej płaszczyzną. Tę
część, choć zawiera szereg pięknych wyników, pominiemy jako zbyt techniczną.
Dalszym ciągiem O kuli i walcu jest rozprawa O konoidach i sferoidach,
dotycząca krzywych stożkowych. Znajdujemy tam m.in., dowiedzione metodą
wyczerpywania, wzory na pola powierzchni elips, a przede wszystkim twierdzenia
na temat paraboloid obrotowych i hiperboloid obrotowych, figur otrzymywanych
przez przecięcie ich płaszczyznami itd. Znów zbyt techniczny charakter nie
pozwala na omówienie tych wspaniałych wyników w tym miejscu.
Kolejną z zachowanych rozpraw Archimedesa jest O spiralach.
Jeśli półprosta obraca się wokół swego końca ze stałą prędkością kątową, a
jednocześnie, zaczynając od punktu obrotu, ze stałą prędkością liniową porusza
się po niej punkt, to kreśli on spiralę na płaszczyźnie, pisze Archimedes we
wprowadzeniu. Po czym formułuje i dowodzi dwudziestu kilku twierdzeń dotyczących
zwłaszcza linii stycznych do spiral i pól powierzchni zakreślanych przez spirale
i przecinające je linie.
Krótki tekst O liczeniu piasku powstał jako
wprawka w operowaniu wielkimi liczbami, co stanowiło niebagatelny problem jeśli
zważyć na nieporęczność dostępnych wówczas systemów zapisu liczb. Aby uczynić
zadanie prawdziwie ambitnym, Archimedes odwołuje się do systemu Arystarcha,
zgodnie z którym świat miał być olbrzymi. Choć wspomina, że niektórzy określili
obwód Ziemi na 300 000 stadiów (zob. paragraf następny), to przyjmuje, iż wynosi
on 3 000 000 stadiów. Podczas gdy Arystarch obliczył, że średnica Słońca jest od
18 do 20 razy większa niż średnica Księżyca, to Archimedes zakłada, że ten
stosunek wynosi 30. Tarcza słoneczna zajmuje 1/1000 część zodiaku (faktycznie
1/720), co prowadzi do wniosku, że Słońce oddalone jest o 10 000 średnic Ziemi.
Kolejne, najzupełniej arbitralne, założenie jest takie, iż stosunek średnicy
Ziemi do odległości Ziemia-Słońce jest taki, jak stosunek odległości
Ziemia-Słońce do średnicy sfery gwiazd stałych. Obliczona na tej podstawie
średnica sfery gwiazd stałych wynosi nieco poniżej 1 000 000 razy 10 000 razy 10
000 stadiów. Założenie 5 głosi, iż w kulce o średnicy równej 1/40 szerokości
palca mieści się 10 000 ziaren piasku. Stąd po obliczeniach otrzymujemy, że
„sfera o rozmiarach, jakie Arystarch przypisuje sferze gwiazd stałych
pomieściłaby liczbę ziaren piasku mniejszą niż 1 000 000 jednostek ósmego rzędu
liczb”, co w dzisiejszych oznaczeniach zapiszemy jako 1063.
W pewnym
greckim rękopisie odkryto zadanie, jakie Archimedes miał przesłać
Eratostenesowi. Chodziło o policzenie krów i byków w Trzodzie Słońca przez
rozwiązanie pewnego układu równań. Liczba ta, podana przez komputer w 1965 r.,
wynosi w przybliżeniu 7.76 ∙ 10206544.
Zachował się też Stomachion
(„żołądek”), w którym uczony oblicza pola powierzchni 14 fragmentów łamigłówki,
z których na wiele sposobów można ułożyć kwadrat. Rozprawa
O równowadze płaszczyzn
lokuje się na pograniczu matematyki i statyki. Już przed Archimedesem
sformułowano prawa dźwigni, przede wszystkim to, że jeśli na jednorodnej belce
podpartej w połowie położymy dwa ciężary, to belka pozostanie w równowadze gdy
stosunek ciężarów będzie równy odwrotności ich odległości od punktu podparcia.
Tekst otwiera siedem postulatów, wyraźnie naśladujących postulaty Euklidesa.
Trzy pierwsze odnoszą się do sytuacji przedstawionej na powyższym rysunku: „1.
Równe ciężary w równych odległościach pozostają w równowadze” itd. Po czym mamy
postulaty odnoszące się do figur: „4. Kiedy równe i podobne figury płaskie
pokrywają się gdy zostaną do siebie przyłożone, ich środki ciężkości również się
pokrywają” itd. Na tej podstawie Archimedes dowodzi 15 twierdzeń, np.
Jeśli dwa równe ciężary nie mają tego
samego środka ciężkości, to środek ciężkości obu wziętych razem znajduje się w
środkowym punkcie linii łączącej ich środki ciężkości. [Twierdzenie 4]
(...) środek ciężkości dowolnego trójkąta
znajduje się na przecięciu linii przeprowadzonych z dowolnych dwóch kątów do
środków boków im przeciwnych. [Twierdzenie 14]
(Oczywiście, jeśli mamy to odnieść do
świata widzialnego, chodzi o trójkąt wykonany z jednorodnego materiału o
identycznej wszędzie grubości.) W księdze II znajdujemy 10 dowiedzionych
twierdzeń dotyczących środków ciężkości wycinków paraboli.
Czytając
teksty Archimedesa czytelnik wciąż zastanawia się, jak wpadł on na prezentowane
twierdzenia – nie podaje bowiem wyprowadzeń wzorów, a jedynie ich dowody.
Ciekawość naszą po części zaspokaja list do Eratostenesa, zatytułowany
Metoda twierdzeń mechanicznych
(odkryty w 1906 r. pod tekstem modlitw na średniowiecznym pergaminie). Uczony z
Syrakuz wyznaje:
(...) pewne
zagadnienia stały się dla mnie jasne najpierw przy użyciu metody mechanicznej,
choć później muszą one zostać dowiedzione geometrycznie, gdyż ich badanie za
pomocą wspomnianej metody nie dostarcza prawdziwego dowodu. Ale jest oczywiście
łatwiej dostarczyć dowód, gdy już wcześniej, za pomocą tej metody, zyskaliśmy
pewną wiedzę na temat tych zagadnień, niż znaleźć go bez wcześniejszej wiedzy.
Chodzi o rozważania dotyczące warunku
równowagi dźwigni dwustronnej, na której jednym ramieniu wisi figura o znanej
powierzchni, a na drugim figura stanowiąca przedmiot dociekań. Obie figury
dzielone są na nieskończenie wiele linii, które parami się równoważą – co w
prosty sposób prowadzi do wzorów na powierzchnię. Archimedes stosuje też ję
technikę do brył, które z kolei dzielone są na nieskończenie wiele równoważących
się parami płaszczyzn – co umożliwia wyprowadzenie wzorów na objętość jednej z
brył na podstawie znanego już wzoru na objętość drugiej.
Współczesnemu czytelnikowi trudno oprzeć
się wrażeniu, że Archimedes stoi tu na progu odkrycia procedur zwanych
całkowaniem, a sformułowanych w II połowie XVII wieku. Jak na ironię, posługując
się metodą wyprzedzającą własną epokę o dwa tysiące lat uważa ją jedynie za
prowizoryczny wstęp do prawdziwych badań matematycznych.
Metoda „mechaniczna” i „geometryczna” użyte są równolegle w rozprawie
Kwadratura paraboli.
Otwierają ją trzy twierdzenia z zaginionej rozprawy Euklidesa o przekrojach
stożkowych, podane bez dowodów. Dwa następne dotyczą własności paraboli. Od
twierdzeń 6 i 7 poczynając rozważa się warunki równowagi dźwigni dwustronnej, na
której jednym ramieniu zawieszono prostokąt, a na drugim trójkąt, trapez, a
wreszcie figurę otrzymaną przez przecięcie paraboli linią prostą. Ciężary,
podobnie jak w rozprawie O
równowadze płaszczyzn,
traktuje się jako proporcjonalne do powierzchni. Umożliwia to wreszcie
dowiedzenie twierdzenia 17, zgodnie z którym „pole powierzchni dowolnego
segmentu paraboli jest równe czterem trzecim trójkąta mającego tę samą podstawę
co ów segment i taką samą wysokość”.
 Następnie Archimedes przechodzi do metod
czysto matematycznych. Tekst kończy się dowodem twierdzenia 24:
Następnie Archimedes przechodzi do metod
czysto matematycznych. Tekst kończy się dowodem twierdzenia 24:
[Powierzchnia] każdego segmentu, którego
granicę stanowi parabola i cięciwa Qq jest równa czterem trzecim [powierzchni]
trójkąta mającego tę samą podstawę co ów segment i taką samą wysokość.
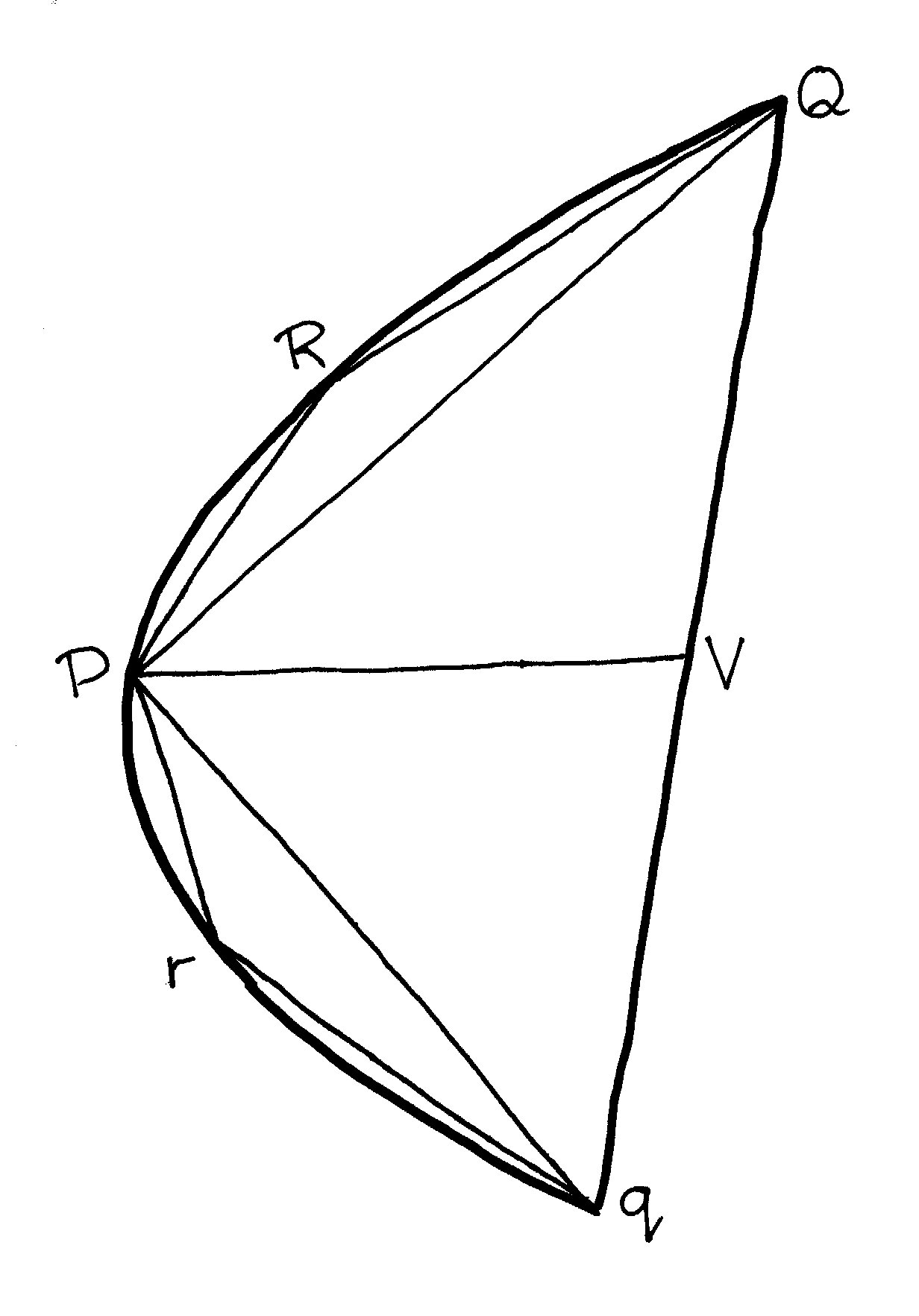
Załączony rysunek obrazuje ideę dowodu:
ciąg trójkątów stopniowo „wyczerpuje” powierzchnię segmentu paraboli. (Punkt V
dzieli odcinek Qq na połowę.) Archimedes dowodzi, korzystając z własności
paraboli, że trójkąty PQR i Pqr mają powierzchnię równą, a ośmiokrotnie mniejszą
od powierzchni PQq (a zatem ich łączna powierzchnia wynosi ¼ powierzchni PQq).
Analogicznie, ośmiokrotnie mniejsza od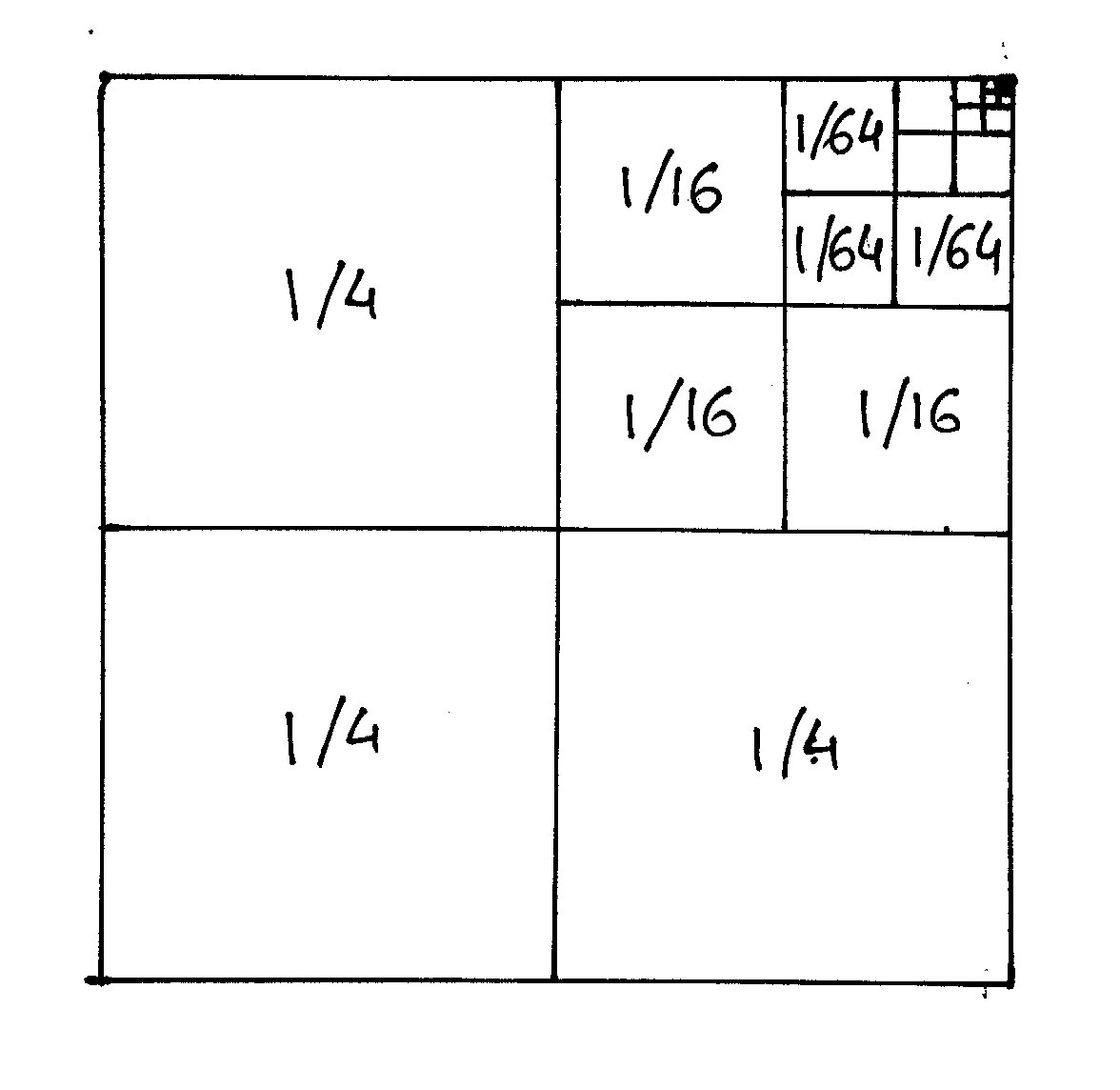 powierzchni PQR będzie powierzchnia
każdego z trójkątów zbudowanych w analogiczny sposób na bokach PR i RQ (a zatem
ich łączna powierzchnia wynosi 1/16 powierzchni PQq). I tak dalej w
nieskończoność. Tym razem Archimedes nie konstruuje ciągu trójkątów opisanych na
rozważanej figurze, ale traktuje pole powierzchni segmentu paraboli jako sumę
pól powierzchni trójkątów wpisanych. Aby rozwiązać całe zadanie, pozostaje
policzyć sumę nieskończonego szeregu:
powierzchni PQR będzie powierzchnia
każdego z trójkątów zbudowanych w analogiczny sposób na bokach PR i RQ (a zatem
ich łączna powierzchnia wynosi 1/16 powierzchni PQq). I tak dalej w
nieskończoność. Tym razem Archimedes nie konstruuje ciągu trójkątów opisanych na
rozważanej figurze, ale traktuje pole powierzchni segmentu paraboli jako sumę
pól powierzchni trójkątów wpisanych. Aby rozwiązać całe zadanie, pozostaje
policzyć sumę nieskończonego szeregu:
1 + 1/4 + 1/16 + 1/64 + 1/256 + ...
Archimedes dokonuje tego sposobem geometrycznym, zilustrowanym na rysunku
(nasz różni się nieco od tego, jaki jest w tekście oryginalnym).
[rys. 19]
Dzielimy kwadrat na cztery równe
kwadraty, następnie jeden z nich dzielimy na cztery równe kwadraty itd. Jak
widać z rysunku, podzieliliśmy cały kwadrat na trzy równe części, z których
każda składa się z nieskończonego ciągu kwadratów, z których pierwszy ma pole
równe1/4 pola powierzchni całości, drugi 1/16 pola powierzchni całości, trzeci
1/64 itd. A zatem:
1/4 + 1/16 + 1/64 + 1/256 + ... = 1/3.
Nic nie wiemy
o tym, aby Arystoteles miał jakiegoś poprzednika w dziedzinie hydrostatyki.
Wyniki swych badań przedstawił w dziele O ciałach pływających.
Zaczyna się od twierdzenia związanego z kulistością Ziemi:
Powierzchnia dowolnej cieczy w [stanie]
spoczynku jest powierzchnią sfery, której środek pokrywa się ze środkiem Ziemi.
[Twierdzenie 2]
Po czym mamy szereg twierdzeń łącznie
składających się na tzw. prawo Archimedesa, z których najważniejsze to:
Jeśli dowolne ciało stałe lżejsze niż
ciecz zostanie w niej umieszczone, to zanurzy się ono tak głęboko, że waga tego
ciała będzie równa wadze wypartej cieczy. [Twierdzenie 5]
Jeśli ciało stałe cięższe niż ciecz
zostanie w niej umieszczone, opadnie na dno i będzie, gdy zważy się je w cieczy,
lżejsze od swej prawdziwej wagi o wagę wypartej cieczy. [Twierdzenie 7]
W księdze II Archimedes stosuje te prawa,
w połączeniu z wynikami swych prac matematycznych, aby ustalić warunki równowagi
paraboloid obrotowych zanurzonych w cieczy. Te ogromnie jak na swoje czasy
wyrafinowane badania – których znów z uwagi na zbyt techniczny charakter nie da
się tu omówić – można traktować jako znaczący krok w stronę teorii budowy
statków. A cała rozprawa, bardziej może niż jakikolwiek inny tekst powstały w
starożytności, przypomina prace dziś zwane „naukowymi”.
Archimedes
słynął też jako konstruktor, choć na ten temat mamy tylko przekazy wtórne. Miał
udoskonalić tzw. śrubę Archimedesa, służącą do wypompowywania wody z olbrzymiego
okrętu Syrakuzja (a przypominającą wałek z maszynki do mięsa). Jego dokonania
inżynierskie znamy głównie z opowieści o oblężeniu Syrakuz. Układy luster,
skupiających odbite światło Słońca w jednym miejscu, miały zapalać rzymskie
okręty. Mimo ponawianych prób nikomu w naszych czasach – przy użyciu dostępnych
w III w. p.n.e. zwierciadeł – nie udało się tego dokonać, co podważa
wiarygodność tych relacji. (Udało się co prawda zapalić po kilku minutach stos
drewna leżącego nieruchomo, ale trudno sobie wyobrazić zapalenie płynącego
okrętu, chronionego w dodatku przez załogę.) Dużo bardziej wiarygodne są, w
świetle współczesnych prób, opowieści o wyrzutniach pocisków, a także o
dźwigach, które miały chwytać okręty i przewracać je. (Z nimi wiąże się słynna
uwaga, jaką Archimedes miał wypowiedzieć do króla Hierona: „gdyby miał drugą
ziemię, przeszedłby na nią i poruszył istniejącą” [Plutarch,
Żywot Marcellusa 14]. W wersji Papposa z Aleksandrii uwaga ta brzmiała: „Dajcie mi punkt
podparcia, a poruszę Ziemię” [Synagoge
VIII]. Nie budzi natomiast zaufania relacja Witruwiusza o tym, jak wpadłszy
podczas kąpieli na pomysł wyznaczenia objętości królewskiej korony przez
zanurzenie jej w wodzie, Archimedes biegł nago przez miasto krzycząc
eureka, czyli „odkryłem” [O architekturze
IX]).
Pisma Archimedesa najbardziej ze wszystkich, jakie pozostawiła nam starożytność, mają
charakter „naukowy” we współczesnym tego słowa znaczeniu. Nie tylko był
najbardziej twórczym matematykiem tego okresu, ale w rozprawach O równowadze płaszczyzn
i O ciałach pływających po raz
pierwszy w znanej nam historii ludzkości na taką skalę zastosowano matematykę do
opisu zjawisk przyrody. (Wcześniej uczynił to wprawdzie Eudoksos z Knidos, ale w
odniesieniu do ruchów ciał niebieskich, którym przypisywano wówczas inną naturę
niż ruchom ciał w świecie podksiężycowym.) Zakres zastosowań był wprawdzie
ograniczony do statyki i hydrostatyki, ale otwierało to drogę do tworzenia,
przez analogię, zastosowań kolejnych. Trudno oprzeć się myśli, że gdyby
wytyczoną przez Archimedesa drogą podążyło grono zdolnych badaczy, nauki
przyrodnicze mogłyby się narodzić tysiąc osiemset lat wcześniej niż to
faktycznie się stało. Niestety, ekspansja Rzymu zniweczyła te szanse. Na użycie
matematyki w skali takiej, z jaką mamy do czynienia w rozprawach Archimedesa, do
badań nad przyrodą trzeba było czekać aż do Galileusza.
A jednak nie
jest jasne, czy Archimedesa można już nazwać „naukowcem”. (Dlatego w odniesieniu
do niego i innych bohaterów tego rozdziału używamy bezpieczniejszego określenia
„uczony”. Warto zaznaczyć, że w starożytnej grece nie ma słowa, które wprost
odpowiadałoby naszemu „nauka”.) Otóż jeśli porównujemy matematyczno-przyrodnicze
dzieła Archimedesa z Galileuszowymi Rozmowami i dowodzeniami matematycznymi (1638),
od razu rzuca się w oczy brak u uczonego z Syrakuz systematycznych odwołań do
wyników eksperymentów. Trudno sobie wprawdzie wyobrazić, aby prawo wyporu
zostało otrzymane inaczej niż w wyniku pomiarów, ale i tak jest niejasne, czy
autor O równowadze płaszczyzn
prowadził systematyczne badania eksperymentalne. A bez tego o nauce – tak jak my
dziś to słowo pojmujemy – mowy być nie może. Nauka – taka, jaką znamy od
Galileusza poczynając – nie rozwinie się, jeśli wyniki badań nie będą miały
zastosowań praktycznych. Mamy związane z tym ważne świadectwo Plutarcha w
Cheronei:
Zajmowanie się mechaniką i w ogóle każdą
sztuką, obliczoną na przydatność w potrzebie, [Archimedes] uważał za coś
nieszlachetnego, za rzecz rzemieślniczą. (...) Jakkolwiek jednak był wynalazcą
wielu wspaniałych rzeczy, przyjaciół swoich i krewnych prosił, jak mówią, tylko
o to, żeby po jego śmierci postawili mu na grobie walec obejmujący kulę z
napisem podającym obliczenie różnicy objętości bryły obejmującej w stosunku do
objętej. [Żywot Marcellusa
17]
Oczywiście ta opinia, spisana w trzy stulecia
po śmierci uczonego, jest sama w sobie mało wiarygodna. Ale potwierdza ją szereg
faktów. Po pierwsze, nic nie wiadomo o tym, aby Archimedes napisał jakąś pracę
na temat swych wynalazków. (Podczas gdy Galileusz dwie pierwsze księgi
Rozmów poświęca specjalnie zagadnieniom „obliczonym na przydatność w potrzebie” i robi
to z dumą.) Po drugie, zarówno rozprawie O równowadze płaszczyzn,
jak i O ciałach pływających
nadał postać tak matematyczną, jak to tylko było możliwe. Po trzecie, nawet
omówioną powyżej „metodę twierdzeń mechanicznych” przez to, że wiązały się z nią
pewne wyobrażenia o praktycznych pomiarach – choć faktycznie niczego się w
trakcie jej stosowania nie waży – uznał za wstęp tylko do prawdziwych badań
matematycznych. W sumie, choć ziarna myślenia naukowego zostały przez
Archimedesa rzucone, to na ich rozwój trzeba było czekać osiemnaście wieków.
Zdaje się, że bez politycznej emancypacji
rzemieślników nie ma społecznych warunków, w jakich mogłyby się rozwinąć nauki
przyrodnicze. A do tego doszło dopiero w nowożytnej Europie. Panujące w
starożytności i średniowieczu stosunki władzy i własności dusiły rozwijające się
nauki w zarodku. Tu jednak zaczynamy daleko wykraczać poza tematykę tej książki.
6. O pomiarze Ziemi Eratostenesa z Kyrene
Eratostenes urodził się w 276 r. p.n.e.
na terenie obecnej Libii. Czas jakiś spędził w Atenach, a wreszcie po
przeniesieniu się do Aleksandrii został ok. 240 r. p.n.e. trzecim kustoszem
Biblioteki. Uczonym był wszechstronnym, ale krążyła o nim opinia, że w żadnej
dziedzinie nie osiągnął najwyższego poziomu. Zmarł w 194 r. p.n.e. Wszystkie
jego dzieła zaginęły.
Tekst Platonicus
poświęcił, zgodnie z pitagorejsko-platońską tradycją, zarówno arytmetyce i
geometrii, jak i muzyce. Zajmował się w nim m.in. tradycyjnym (a
nierozwiązywalnym) problemem, jak metodami geometrycznymi skonstruować sześcian
o objętości dwukrotnie większej od objętości sześcianu danego. Sformułował też
ideę tzw. „sita Eratostenesa”, pozwalającego znaleźć wszystkie liczby pierwsze
nie większe od danej liczby n:
zostaw 2 ale usuń wszystkie jego wielokrotności, następną z pozostałych liczb
jest 3, zostaw 3 ale usuń wszystkie jego wielokrotności, następną z pozostałych
liczb jest 5, zostaw 5 itd. Ten prosty pomysł dał początek technikom
matematycznym z powodzeniem stosowanym po dzień dzisiejszy.
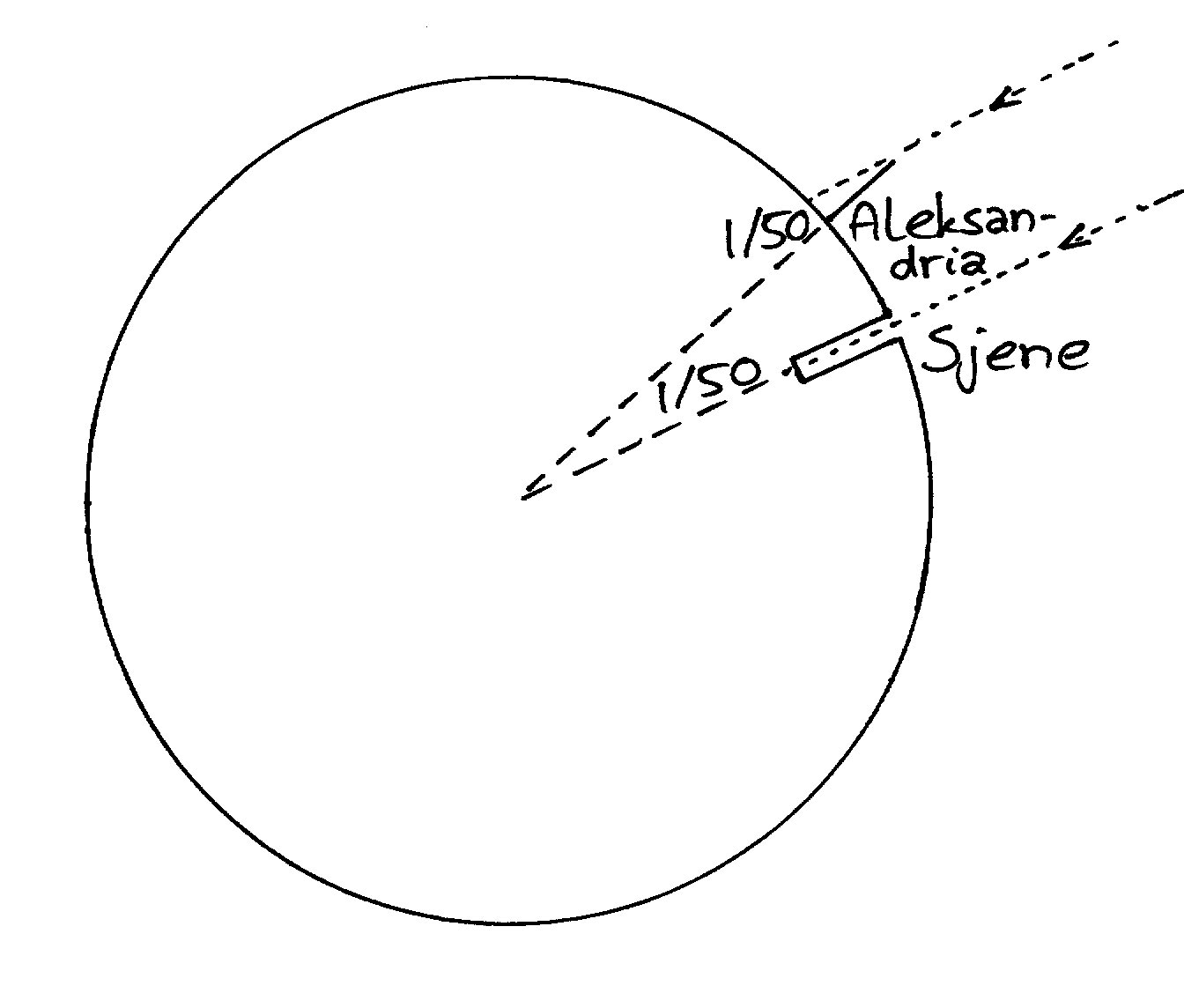 Najsłynniejszym dziełem Eratostenesa było O pomiarze Ziemi,
które znamy dzięki relacjom Strabona z Amazei, i innych. Wiedząc o tym, że w
dniu przesilenia letniego Słońce w Syene (obecnie Asuan nad Nilem) świeci w samo
południe pionowo w górze, Eratostenes zmierzył kąt, pod jakim w tym samym czasie
pada cień w Aleksandrii. Wynosił on 1/50 kąta pełnego. Syene leżało ok. 5000
stadiów na południe od ujścia Nilu. Na podstawie pomiarów odległości Słońca,
dokonanych kilkadziesiąt lat wcześniej przez Arystarcha, Eratostenes mógł
przyjąć, że z bardzo dobrym przybliżeniem promienie słoneczne w obu miastach są
równoległe.
Najsłynniejszym dziełem Eratostenesa było O pomiarze Ziemi,
które znamy dzięki relacjom Strabona z Amazei, i innych. Wiedząc o tym, że w
dniu przesilenia letniego Słońce w Syene (obecnie Asuan nad Nilem) świeci w samo
południe pionowo w górze, Eratostenes zmierzył kąt, pod jakim w tym samym czasie
pada cień w Aleksandrii. Wynosił on 1/50 kąta pełnego. Syene leżało ok. 5000
stadiów na południe od ujścia Nilu. Na podstawie pomiarów odległości Słońca,
dokonanych kilkadziesiąt lat wcześniej przez Arystarcha, Eratostenes mógł
przyjąć, że z bardzo dobrym przybliżeniem promienie słoneczne w obu miastach są
równoległe.
[rys. 20]
A zatem 1/50 kąta pełnego to również kąt,
którego wierzchołek znajduje się w środku Ziemi, zaś ramiona przechodzą przez
Syene i Aleksandrię. Stąd natychmiast otrzymujemy, że obwód Ziemi wynosi 50 x
5000 stadiów = 250 000 stadiów.
Nie wiemy, ile wynosił stadion używany
przez Eratostenesa. Przy różnych przyjmowanych w starożytności wartościach
podana wartość obwodu Ziemi mogła zgadzać się z obecnie przyjętą z dokładnością
do 1% (co byłoby wynikiem szczęśliwego zbiegu okoliczności, a nie precyzji
procedur pomiarowych), w każdym razie błąd nie był większy niż kilkanaście
procent.
Eratostenes wniósł spory wkład do
geografii. Wyznaczył ze sporą dokładnością drogę Nilu, opisał tereny
dzisiejszego Jemenu. A przede wszystkim twierdził – wbrew rozpowszechnionym
błędnym poglądom na ten temat – że wylewy Nilu są powodowane obfitymi opadami
deszczy w pobliżu jego źródeł.
Miał też
zajmować się astronomią. Na podstawie danych zgromadzonych podczas zaćmień
wyznaczył podobną wartość odległości Ziemia-Księżyc jak Arystarch, natomiast
Słońce lokował 1030 razy dalej. Nachylenie osi ziemskiej do płaszczyzny
ekliptyki miał, według świadectwa Ptolemeusza, określić na 11/83 kąta półpełnego
(czyli 23051')
– co jest wartością podejrzanie dokładną. Sporządził katalog podający położenia
675 gwiazd.
Twierdzi się, że próbował określić daty
najważniejszych wydarzeń politycznych i kulturowych od upadku Troi.
7. Apollonios z Perge o krzywych stożkowych i o niebie
Działało w tym czasie kilku znakomitych
matematyków, o dokonaniach których – nie licząc Apolloniosa – wiemy coś tylko na
podstawie rozproszonych przekazów.
Nikomedes (ok. 280-ok. 210 p.n.e.), który
krytykował Eratostenesa za jego metodę wyznaczania wartości średnich
proporcjonalnych (związaną z zagadnieniem podwojenia sześcianu), skonstruował
krzywą, znaną jako konchoida Nikomedesa. Można się nią posłużyć aby dokonać
trysekcji kąta – ale, rzecz jasna, nie można jej wykreślić za pomocą linii i
cyrkla.
Konon z Samos (ok. 280-ok. 220 p.n.e.) odkrył
krzywą, znaną jako spirala Archimedesa. Obu uczonych łączyła, jak się zdaje,
serdeczna przyjaźń. A choć Apollonios zbyt wysokiego zdania o Kononie nie był,
to dokonania tego ostatniego stanowią chyba podstawę Księgi IV
Konika.
Napisał też Konon dzieło o astronomii, poświęcone m.in. zaćmieniom Słońca.
Dionizodoros z Kaunos (ok. 250-ok.190 p.n.e.)
podał rozwiązanie zagadnienia, które sformułował Archimedes w
O kuli i walcu: jak za pomocą płaszczyzny podzielić
kulę na dwie części, których stosunek objętości wyniesie
m/n. Wymaga to, z naszego punktu widzenia, rozwiązania równania trzeciego stopnia.
Dionizodoros uporał się z tym wyznaczając punkty przecięcia paraboli i
hiperboli. Tej zachwycającej konstrukcji, znanej dzięki komentarzowi Eutokiosa z
Askalonu (I poł. VI w.), nie będziemy tu, z uwagi na jej wysoce techniczny
charakter, omawiać.
W komentarzu Eutokiosa do O kuli i walcu
Archimedesa czytamy też o krzywej zwanej cisoidą, którą posłużył się Diokles z
Karystos (ok. 240-ok.180) w celu podwojenia sześcianu.
Diokles był też autorem traktatu O zwierciadłach zapalających,
ocalałego w arabskim przekładzie. W pierwszej części analizował własności
zwierciadła parabolicznego, które skupia, jak wykazał, równoległą wiązkę światła
w jednym punkcie. Badał też własności zwierciadła sferycznego. Dalsze partie
tekstu poświęcone są Archimedesowemu problemowi przecinania kuli płaszczyzną, a
także zagadnieniu podwojenia sześcianu. Wreszcie Diokles podejmuje zagadnienie
skonstruowania takiego zwierciadła, aby zogniskowane promienia Słońca, w trakcie
jego dziennego ruchu po niebie, nakreśliły daną krzywą.
Apollonios urodził się ok. 262 r. p.n.e. w
Perge. W Aleksandrii studiował matematykę pod kierunkiem uczniów Euklidesa. Dość
wcześnie napisał w ośmiu księgach rozprawę o krzywych stożkowych, powstających w
wyniku przecięcia stożka płaszczyzną – czyli o elipsie, paraboli i hiperboli.
Tekst zakończył w pośpiechu, aby zdążyć przed wyjazdem z Aleksandrii jednego ze
swych nauczycieli. Przeczytał go Eudemos z Pergamonu, a jego krytyczne uwagi
skłoniły Apolloniosa do dalszych prac, których owocem stała się druga i
ostateczna wersja Konika
(Stożkowe).
Była już mowa
o tym, że krzywe stożkowe odkrył Menajchmos, a rozprawy na ich temat napisali
Euklides i Aritajos Starszy. Ale że ich teksty zaginęły – zapewne przestano je
kopiować, gdy po wydaniu Konika stały się zbędne – to nie wiadomo,
jaki wkład w zagadnienie wniósł sam Apollonios.
Z liczącego pierwotnie osiem ksiąg tekstu
dzieła zachowały się po grecku księgi od I do IV, zawierające, jak pisze autor,
elementarne wprowadzenie do tematu. Mamy też arabski przekład ksiąg od I do VII.
Zachowana część zawiera 387 twierdzeń z dowodami. Najważniejsza jest księga V,
poświęcona głównie zagadnieniu, jak z danego punktu narysować normalną do
krzywej stożkowej. Zawartości Konika,
ze względu na wysoce techniczny charakter tekstu, nie będziemy tu jednak
omawiać.
Znamy z grubsza – na podstawie
starożytnych komentarzy i odwołań u autorów arabskich – zawartość kilku innych
dzieł matematycznych Apolloniosa. Miał w nich m.in. podać wartość liczby π
dokładniejszą niż wyznaczona przez Archimedesa. Miał też wykazać, że zwierciadło
sferyczne nie skupia równoległej wiązki świata w jednym punkcie.
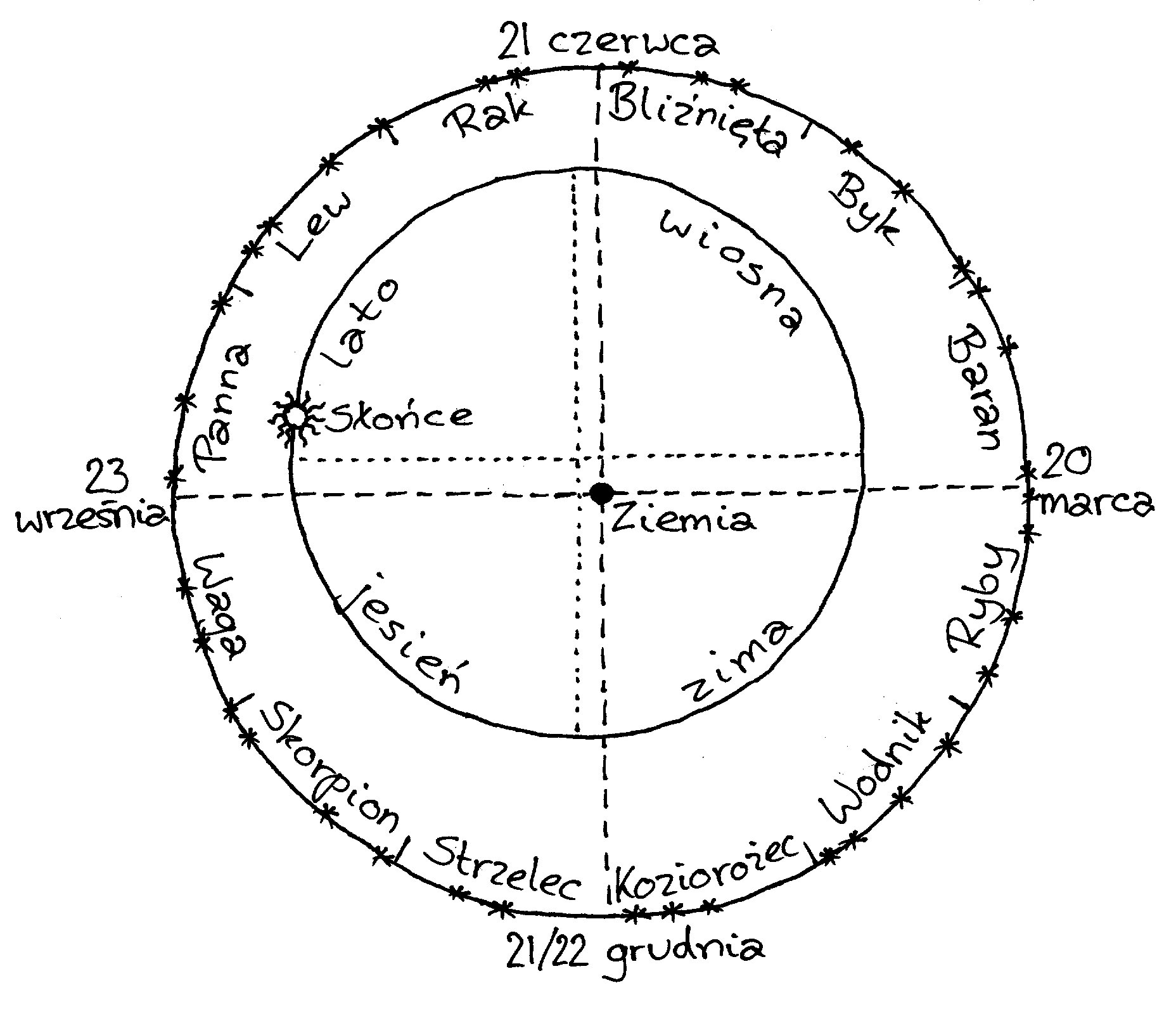 Bardzo ważne miały się okazać jego prace
z zakresu astronomii – które wówczas zaliczano do matematyki – poświęcone
ruchowi Słońca. Jeśli dokładnie wyznaczymy dni, w których Słońce wschodzi i
zachodzi najdalej na północ (tego dnia zaczyna się lato), w których wschodzi i
zachodzi po przeciwległych krańcach horyzontu (są to pierwsze dni wiosny i
jesieni), a wreszcie kiedy wschodzi i zachodzi najdalej na południu (i zaczyna
się zima), to okaże się, że długości pór roku nie są takie same. Dokładniejsze
dane uzyskamy wyznaczając drogę Słońca na tle gwiazd i ustalając, kiedy wchodzi
ono w kolejne znaki zodiaku. Wiosna trwa 92 ¾ dnia, lato 93 ¾ dnia, jesień 89 ¾
dnia, a zima 89 dni. Dla pitagorejczyka bądź platonika jest to spostrzeżenie
bardzo niemiłe, uważali oni bowiem, że ciałom niebieskim przystoją tylko ruchy
doskonałe. Apollonios znalazł rozwiązanie zgodne z pitagorejsko-platońskimi
ideałami: Słońce, wirując ruchem dobowym wraz z gwiazdami, porusza się też w
stosunku do gwiazd „doskonałym” ruchem jednostajnym po okręgu, tyle
Bardzo ważne miały się okazać jego prace
z zakresu astronomii – które wówczas zaliczano do matematyki – poświęcone
ruchowi Słońca. Jeśli dokładnie wyznaczymy dni, w których Słońce wschodzi i
zachodzi najdalej na północ (tego dnia zaczyna się lato), w których wschodzi i
zachodzi po przeciwległych krańcach horyzontu (są to pierwsze dni wiosny i
jesieni), a wreszcie kiedy wschodzi i zachodzi najdalej na południu (i zaczyna
się zima), to okaże się, że długości pór roku nie są takie same. Dokładniejsze
dane uzyskamy wyznaczając drogę Słońca na tle gwiazd i ustalając, kiedy wchodzi
ono w kolejne znaki zodiaku. Wiosna trwa 92 ¾ dnia, lato 93 ¾ dnia, jesień 89 ¾
dnia, a zima 89 dni. Dla pitagorejczyka bądź platonika jest to spostrzeżenie
bardzo niemiłe, uważali oni bowiem, że ciałom niebieskim przystoją tylko ruchy
doskonałe. Apollonios znalazł rozwiązanie zgodne z pitagorejsko-platońskimi
ideałami: Słońce, wirując ruchem dobowym wraz z gwiazdami, porusza się też w
stosunku do gwiazd „doskonałym” ruchem jednostajnym po okręgu, tyle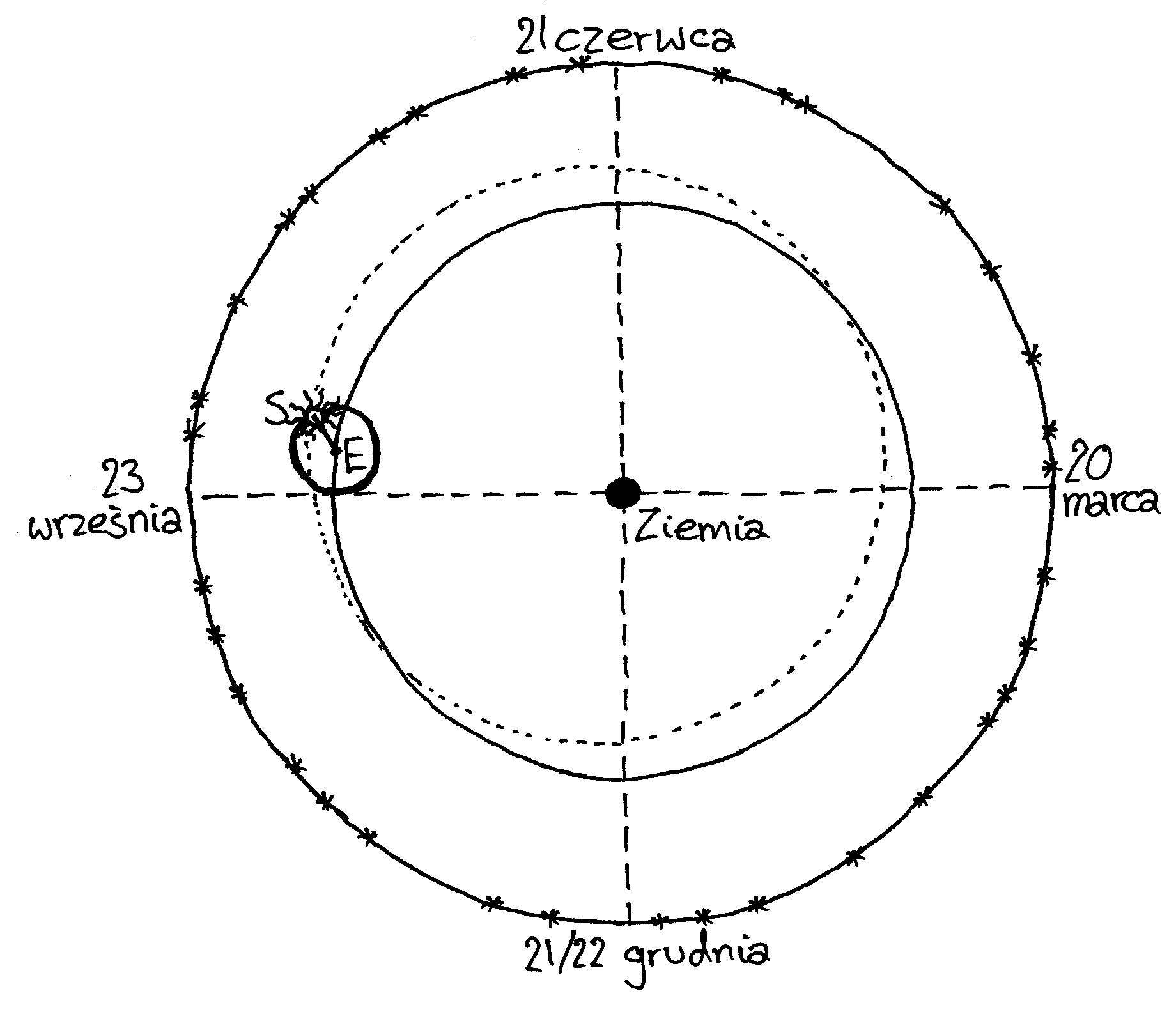 że środek
okręgu nie znajduje się w środku Ziemi. Skoro spoglądamy na Słońce spoza środka
jego orbity, to zdaje się nam, że w porusza się ono na tle gwiazd raz szybciej a
raz wolniej – co pociąga za sobą różną długość pór roku.
że środek
okręgu nie znajduje się w środku Ziemi. Skoro spoglądamy na Słońce spoza środka
jego orbity, to zdaje się nam, że w porusza się ono na tle gwiazd raz szybciej a
raz wolniej – co pociąga za sobą różną długość pór roku.
Na tym Apollonios nie poprzestał.
Stwierdził, że analogiczny wynik da inne założenie. A mianowicie Słońce S
znajduje się na obwodzie okręgu, nazwanego później epicyklem, zaś środek
epicyklu E wędruje ruchem jednostajnym po okręgu, którego środek pokrywa się ze
środkiem Ziemi. (Ponadto, rzecz jasna, Słońce obiega Ziemię ruchem dobowym wraz
z gwiazdami).
Dzisiejszemu czytelnikowi wyda się
dziwne, po co umieszczać Słońce na epicyklu, a nie po prostu na końcu odcinka
ES. Zaważyła zapewne pitagorejska wiara w doskonałość okręgu. Później miało to w
niezamierzony sposób zainspirować kolejne pokolenia astronomów.
Apollonios z Perge, który zmarł zapewne
między 190 a 170 r. p.n.e., był – po Euklidesie i Archimedesie – ostatnim
wielkim matematykiem świata starożytnego. Natomiast w astronomii znalazł wkrótce
godnego siebie następcę.
8. Trygonometria i astronomia Hipparcha z Nikai
W II w. p.n.e. działało jeszcze paru twórczych matematyków.
Zenodoros z Aten (ok. 200-ok. 140 p.n.e.)
napisał rozprawę O figurach izometrycznych,
która zaginęła, ale szereg zawartych tam twierdzeń znamy dzięki komentarzom
Papposa z Aleksandrii (I poł. IV w.) i Teona z Aleksandrii (II poł. IV w.).
Hypsikles z Aleksandrii (ok.190 p.n.e.–ok.120
p.n.e.) był autorem tzw. XIV Księgi Elementów, dotyczącej wpisywania
brył foremnych w sferę. Dowiódł tam m.in., że stosunek powierzchni
dwunastościanu foremnego i dwudziestościanu foremnego, wpisanych w tę samą
sferę, jest taki sam, jak stosunek ich objętości i wynosi
√10/3(5-√5). Napisał też traktat
astronomiczny, w którym dzielił Zodiak (za Babilończykami) na 3600
i badał czasy wschodów i zachodów gwiazd w zależności od pory roku (wyniki
obliczeń, jakie podał, są błędne, co zapewne należy przypisać temu, że nie
dysponował funkcjami trygonometrycznymi).
Perseusz, który żył zapewne w II w. p.n.e., a o którym wiemy coś jedynie ze
wzmianek w pismach Geminosa (I w.) i Proklosa (V w.), badał krzywe, które
otrzymuje się z przecięcia płaszczyzną powierzchni, otrzymanej przez obracanie w
przestrzeni koła wokół stałej osi znajdującej się w tej samej co ono
płaszczyźnie. Wyróżnia się pięć rodzajów takich krzywych, zależnie od tego, czy
oś obrotu przecina koło, jest z nim styczna, czy znajduje się poza nim.
W latach 145-144 p.n.e. Ptolemeusz VII,
zaraz po objęciu władzy, zaczął – może z lęku przed Rzymianami, którzy właśnie
pokonali Kartaginę i zajęli Grecję – prześladować helleńskich arystokratów.
Podejrzewa się, że doprowadziło to do wyjazdu z Aleksandrii matematyków i
badaczy.
Hipparch z Nikai urodził się w w Bitynii ok.
190 r. p.n.e., w latach 147-127 sporządził tabele astronomiczne – i to wszystko,
co wiemy o ostatnim wielkim uczonym epoki hellenistycznej. Zaglądając do tabel
można ze sporą dokładnością stwierdzić, że pierwsze obserwacje dokonane zostały
z Aleksandrii, natomiast późniejsze z wyspy Rodos. Jeśli Hipparch przeprowadzał
je osobiście, to można domniemywać, że był jednym z uczonych, którzy w czasie
rządów Ptolemeusza VII opuścili miasto. Z jego dzieł zachował się tylko jeden
tekst, w dodatku o marginalnym znaczeniu:
Komentarz do Phainomena Eudoksosa i Aratusa.
Głównym źródłem informacji o jego pracach jest dla nas Ptolemeusz (zob. rozdz.
XV.3), który uważał Hipparcha za swego głównego poprzednika.
Szeroko wykorzystywał dorobek matematyków
i astronomów chaldejskich z Mezopotamii (być może to oni dokonali niektórych z
przypisywanych mu odkryć). Sporządził na tej podstawie kalendarz astronomiczny
sięgający wstecz bodaj do VII w. p.n.e. Używał – co było w świecie
hellenistycznym nowością – chaldejskiego podziału kąta pełnego na 360 stopni.
Niektórzy uważają go za twórcę
trygonometrii: sporządził – zapewne na użytek swych badań astronomicznych –
tabelę długości cięciw w zależności od kąta α, którego wierzchołek stanowił
środek okręgu, a ramiona przechodziły przez punkty przecięć cięciwy z okręgiem
(co, po podzieleniu przez promień, daje 2sinα/2).
Według
Historii naturalnej
Pliniusza Starszego (ok. 77 n.e.) w czasach Hipparcha miała pojawić się na
niebie nowa gwiazda. Obserwując ją uczony zaczął wątpić w prawdziwość
tradycyjnej wiary w niezmienność świata ponad Księżycem – i aby następne
pokolenia mogły sprawdzić, czy gwiazdy nie zmieniają powoli względnych położeń,
a ponadto czy nie powstają i nie giną, przystąpił do sporządzenia dokładnej mapy
nieba. Posługiwał się przy tym specjalnie skonstruowanymi przyrządami, lepszymi
niż te, jakimi dysponowali jego poprzednicy. Po latach pracy określił we
współrzędnych ekliptycznych położenia co najmniej 850 gwiazd.
Katalog ten stanowił następnie podstawę
największego odkrycia Hipparcha. Porównując wyniki własnych obserwacji z
zapisami sprzed 160 lat, odkrył powolne przemieszczanie się punktów równonocy ze
wschodu na zachód na tle gwiazd stałych (co dziś wyjaśniamy precesyjnym obrotem
osi ziemskiej, dokonującym się raz na 26 tysięcy lat) i ze sporą dokładnością
określił jego wartość.
Ustalił długość roku słonecznego na 365 +
1/4 – 1/300 dnia (co różni się od wartości podawanej dziś tylko o ok. 6 minut).
Za pomocą tzw. dioptry stwierdził, że kątowe rozmiary tarczy Słońca nie zmieniają się,
natomiast Księżyca tak, zaś średnio Księżyc zajmuje na niebie 360/650 stopnia.
Następnie, jak czytamy w zachowanych fragmentach komentarza Papposa z
Aleksandrii do Almagestu Ptolemeusza:
W I księdze O rozmiarach i odległościach
[Hipparch] czyni spostrzeżenie następujące: zaćmienie Słońca, które w okolicach
wokół Hellespontu było zupełnym przysłonięciem całej tarczy słonecznej, tak że
żadna jej część nie była widoczna, ale w Aleksandrii w Egipcie przysłonięta ona
została w przybliżeniu w czterech piątych. Na tej podstawie wykazuje w księdze
I, że, jeśli za jednostkę odległości przyjmiemy promień Ziemi, to najmniejsza
odległość do Księżyca wynosi 71, a największa 83. Średnio więc 77 (...). Potem
znów w księdze II O rozmiarach i odległościach
pokazuje, na podstawie licznych rozważań, że, jeśli za jednostkę odległości
przyjmiemy promień Ziemi, to najmniejsza odległość do Księżyca wynosi 62,
średnia 67 1/3, zaś odległość do Słońca 490.
(Dziś przyjmujemy, że średnia odległość
między Księżycem a Ziemią wynosi ok. 60 jej promieni.) Łatwo zrozumieć pierwszą
część tego fragmentu. Hipparch oparł się na relacjach o zaćmieniu chyba ze 190
r. p.n.e. Znając położenia obu miast i zakładając, że Słońce jest niesłychanie
daleko, mógł obliczyć odległość do Księżyca (pewne trudności wiązały się z
faktem, że zaćmienie miało miejsce nad ranem, a zatem blisko horyzontu). Druga
część zdaje się odnosić do wyników pomiarów podobnych jak te dokonane sto lat
wcześniej przez Arystarcha.
Hipparch
pracował nad matematyczną teorią ruchu Księżyca – który jest najbardziej
skomplikowany spośród ruchów ciał niebieskich, gdyż nie tylko dość znacznie
zmienia się prędkość wędrówki naszego satelity na tle gwiazd, ale również jego
tor zbacza do 50 w górę i w
dół od płaszczyzny ekliptyki. Na podstawie zapisów chaldejskich Hipparch
określił okres, w jakim zaćmienia Księżyca następują w niemal identycznych
okolicznościach na 126 007 dni i 1 godzinę. Użył zarówno modelu ruchu po kole
ekscentrycznym, jak i modelu ruchu na epicyklu, którego środek porusza się
ruchem jednostajnym po deferencie – oba modele objaśniają rysunki w paragrafie o
modelu ruchu Słońca Apolloniosa. Oparte na dwóch różnych zbiorach obserwacji
obliczenia stosunku ekscentryka do promienia toru Księżyca, a także stosunków
promieni epicyklu i deferentu różniły się nieco.
Nie jest jasne, czy Apollonios i Hipparch wpadli na pomysł – choćby jakościowego –
wykorzystania układu deferent–epicykl tak, jak to uczynił w II w. n.e.
Ptolemeusz (zob. § XVI.2). Ten ostatni zapewnia nas, że Hipparch „nawet nie
zaczął formułować teorii dla pięciu planet, przynajmniej w tych pismach, które
do nas dotarły. Dokonał jedynie kompilacji obserwacji planetarnych, zestawionych
w sposób bardziej użyteczny, a także wykazał za ich pomocą, że te zjawiska nie
zgadzały się z hipotezami astronomów owych czasów” [Almagest
IX,2].
W tekście komentatora arystotelesowskiego
z początków VI w. n.e. znajdujemy jeszcze jedną, ogromnie ważną uwagę.
Hipparch w książce O ciałach
poruszanych w dół przez własny ciężar
powiada, że w przypadku ziemi rzuconej w górę miotająca siła jest przyczyną
ruchu wznoszącego dopóty, dopóki jest silniejsza niż moc rzuconego ciała; im
większa jest siła miotająca, tym szybciej przedmiot porusza się w górę.
Następnie, w miarę jak ta siła się zmniejsza, ruch w górę trwa z prędkością
malejącą, aż wreszcie ciało zaczyna poruszać się w dół pod wpływem własnego
naturalnego impulsu, choć siła wyrzucająca w pewien sposób trwa; w miarę jak ona
słabnie, ciało porusza się w dół coraz szybciej, osiąga zaś prędkość największą,
gdy ta siła znika całkowicie. Przypisuje też tę samą przyczynę ciałom
upuszczonym z wysoka. Gdyż w ich przypadku siła, która je utrzymywała, trwa
przez czas jakiś, a jej przeciwne działanie jest przyczyną, dla której spadające
ciało na początku porusza się wolniej. [Simplikios, De caelo
264,25]
Znajdujemy tu zarys rozwiązania
największej trudności, wobec jakiej stała fizyka Arystotelesa. Wszystko, co się
porusza, jest przez coś poruszane – oto fundamentalne założenie tej teorii. W
przypadku ruchów naturalnych czynnik poruszający tkwi wewnątrz ciała, ale w
przypadku ruchów wymuszonych – a takim jest m.in. ruch ziemi i wody w górę –
czynnikiem poruszającym jest inne ciało, znajdujące się w kontakcie z ciałem
pozostającym w ruchu wbrew swej naturze. Ponieważ rzucony kamień, po utracie
kontaktu z dłonią, styka się jedynie z powietrzem, Arystoteles wnioskował stąd,
że to ono w jakiś sposób zmusza kamień do dalszego przemieszczania się. Ta
koncepcja chyba od samego początku budziła podejrzenia, gdyż powietrze
jednocześnie miało stawiać opór ruchowi ciała i ruch ten podtrzymywać.
Niestety, nie znamy reakcji Stratona na
hipotezę poruszającej mocy powietrza, co byłoby tym ciekawsze, że dopuszczał on
istnienie próżni. Natomiast po jego śmierci w 269 r. Liceum podupadło – i chyba
przestano się tam tego rodzaju zagadnieniami zajmować. Uczeni aleksandryjscy z
III w. p.n.e. chyba fizyki Arystotelesa nie studiowali i nie stosowali – i
trzeba było upływu kolejnych stu lat, aby ktoś się całym problemem przejął i
zaproponował alternatywne rozwiązanie.
Zachowując podstawowe zasady fizyki
Arystotelesa, Hipparch umieszcza czynnik podtrzymujący ruch wewnątrz ciała.
Twierdzi mianowicie, że siła, która pierwotnie ciało poruszyła, albo nawet
utrzymywała nieruchomo poza jego miejscem naturalnym, trwa w ciele jeszcze przez
jakiś czas. Słabnie ona stopniowo – choć przytoczony fragment nie pozwala nam
rozstrzygnąć, czy dzieje się to „z istoty rzeczy”, czy na skutek działania
naturalnej ciężkości.
Przy okazji Hipparch rozwiązywał inny
problem, z jakim fizyka Arystotelesa nie potrafiła się uporać: prędkość ciał
spadających, jak mówi doświadczenie, rośnie.
Tytuł omawianej przez Simplikiosa
rozprawy sugeruje, że koncepcja nabytej siły poruszającej była stosowana jedynie
do analizy ruchów w kierunku góra-dół. Czy Hipparch stosował analogiczne
wyjaśnienia do analizy innych przypadków nie wiemy. Ale jego pomysł zainspirował
siedem wieków później Jana Filoponosa, a w XIV w. Jana Buridana do sformułowania
teorii impetusu, która z kolei utorowała drogę do fizyki nowożytnej. Pierwsza
praca Galileusza, ogłoszona pod koniec XVI w., była wyrafinowanym powtórzeniem
pomysłu Hipparcha – i dopiero potem zaczął on budować swoją koncepcję ruchów
bezwładnych.
Zaraz po Hipparchu poziom intelektualny w świecie hellenistycznym gwałtownie się
obniżył. Zachowały się trzy prace Teodozjusza z Bitynii (ok.
160-ok. 90 p.n.e.). Jedna dotyczy geometrii sfery, druga wyglądu nieba z różnych
szerokości geograficznych, trzecia ruchu Słońca, bardzo im jednak wiele brakuje
do poziom osiąganego wcześniej. Epikurejczyk Zenon z Sydonu
(ok. 150-ok. 70 p.n.e.) krytykował aksjomaty Euklidesa, czynił to jednak jako
filozof raczej niż jako matematyk (choć trafnie, co dziś byśmy mu przyznali,
zdołał tu i ówdzie wykazać, że Euklides w swych dedukcjach czyni pewne
dodatkowe, milczące założenia.
deklaracja dostępności
 Arystarch zakłada (hipoteza 2), że odległość
Księżyca do Ziemi pozostaje stała (co już w tym czasie, z uwagi na mierzalną za
pomocą prostych przyrządów zmianę średnicy widocznej tarczy Księżyca, trzeba
było traktować jako przybliżenie). Hipoteza 3, wynikająca faktycznie z 1 i
obiegowego w tym czasie założenia, że Księżyc jest kulą, głosi, że kiedy widać
połowę tarczy Księżyca, to linia łącząca Ziemię z Księżycem leży pod kątem
prostym do linii łączącej Księżyc ze Słońcem. Hipoteza 4 nie jest z naszego
punktu widzenia hipotezą, ale sprawozdaniem z wyników pomiarów. Głosi ona, że
kiedy widać na niebie jednocześnie półksiężyc i Słońce, dzieli je odległość
kątowa równa 870.
Wobec tego stosunek odległości Słońce-Ziemia S do odległości Słońce-Księżyc K
jest równa tangensowi 870,
ten zaś wynosi ok. 19.
Arystarch zakłada (hipoteza 2), że odległość
Księżyca do Ziemi pozostaje stała (co już w tym czasie, z uwagi na mierzalną za
pomocą prostych przyrządów zmianę średnicy widocznej tarczy Księżyca, trzeba
było traktować jako przybliżenie). Hipoteza 3, wynikająca faktycznie z 1 i
obiegowego w tym czasie założenia, że Księżyc jest kulą, głosi, że kiedy widać
połowę tarczy Księżyca, to linia łącząca Ziemię z Księżycem leży pod kątem
prostym do linii łączącej Księżyc ze Słońcem. Hipoteza 4 nie jest z naszego
punktu widzenia hipotezą, ale sprawozdaniem z wyników pomiarów. Głosi ona, że
kiedy widać na niebie jednocześnie półksiężyc i Słońce, dzieli je odległość
kątowa równa 870.
Wobec tego stosunek odległości Słońce-Ziemia S do odległości Słońce-Księżyc K
jest równa tangensowi 870,
ten zaś wynosi ok. 19. Jeśli podstawimy, zgodnie z poprzednimi
ustaleniami, że K ≈ 19 S, to z porównania trójkątów i po kilku trywialnych
przekształceniach otrzymujemy K ≈ 10 D, tzn. Księżyc odległy jest od Ziemi o ok.
10 jej średnic (dziś przyjmujemy K ≈ 30 D). Wobec tego S ≈ 190 D, zaś stosunek
średnicy Słońca do średnicy Ziemi wynosi ok. 6 2/3. (A zatem Słońce jest o wiele
większe od Ziemi. Pamiętajmy, iż dwieście lat wcześniej oskarżano Anaksagorasa o
bezbożność m.in. dlatego, że twierdził, iż Słońce jest większe od Peloponezu.)
Czy Arystarch znał choćby w przybliżeniu średnicę Ziemi, nie wiadomo. (Zob.
poniżej rozdział o Eratostenesie).
Jeśli podstawimy, zgodnie z poprzednimi
ustaleniami, że K ≈ 19 S, to z porównania trójkątów i po kilku trywialnych
przekształceniach otrzymujemy K ≈ 10 D, tzn. Księżyc odległy jest od Ziemi o ok.
10 jej średnic (dziś przyjmujemy K ≈ 30 D). Wobec tego S ≈ 190 D, zaś stosunek
średnicy Słońca do średnicy Ziemi wynosi ok. 6 2/3. (A zatem Słońce jest o wiele
większe od Ziemi. Pamiętajmy, iż dwieście lat wcześniej oskarżano Anaksagorasa o
bezbożność m.in. dlatego, że twierdził, iż Słońce jest większe od Peloponezu.)
Czy Arystarch znał choćby w przybliżeniu średnicę Ziemi, nie wiadomo. (Zob.
poniżej rozdział o Eratostenesie). Cytowany
fragment z Archimedesa dotyczył innego niż ruch Ziemi zagadnienia – a był to
koronny zarzut, jaki przeciw heliocentryzmowi formułowano do początków XVII w.
Otóż gdyby Ziemia obiegała nieruchome Słońce, to w cyklu rocznym musiałaby
zbliżać się i oddalać od poszczególnych gwiazd. A wobec tego obserwowalibyśmy
zjawisko zwane paralaksą gwiezdną:
kąty, pod jakimi widać na niebie gwiazdy – zwłaszcza te leżące w pobliżu
płaszczyzny ekliptyki – w cyklu rocznym na przemian rosłyby i malały.
Przedstawmy to na rysunku, zaznaczając domniemane położenia Ziemi w jej wędrówce
wokół Słońca w odstępie 3 miesięcy.
Cytowany
fragment z Archimedesa dotyczył innego niż ruch Ziemi zagadnienia – a był to
koronny zarzut, jaki przeciw heliocentryzmowi formułowano do początków XVII w.
Otóż gdyby Ziemia obiegała nieruchome Słońce, to w cyklu rocznym musiałaby
zbliżać się i oddalać od poszczególnych gwiazd. A wobec tego obserwowalibyśmy
zjawisko zwane paralaksą gwiezdną:
kąty, pod jakimi widać na niebie gwiazdy – zwłaszcza te leżące w pobliżu
płaszczyzny ekliptyki – w cyklu rocznym na przemian rosłyby i malały.
Przedstawmy to na rysunku, zaznaczając domniemane położenia Ziemi w jej wędrówce
wokół Słońca w odstępie 3 miesięcy. Zacznijmy od krótkiego tekstu
O wymierzaniu koła,
który otwiera twierdzenie:
Zacznijmy od krótkiego tekstu
O wymierzaniu koła,
który otwiera twierdzenie: We współczesnych oznaczeniach jest to równoważne wzorowi πrl.
Następnie w koło wielkie sfery Archimedes
wpisuje regularny wielokąt ABC... i obraca go wokół osi AA'.
We współczesnych oznaczeniach jest to równoważne wzorowi πrl.
Następnie w koło wielkie sfery Archimedes
wpisuje regularny wielokąt ABC... i obraca go wokół osi AA'. Następnie Archimedes przechodzi do metod
czysto matematycznych. Tekst kończy się dowodem twierdzenia 24:
Następnie Archimedes przechodzi do metod
czysto matematycznych. Tekst kończy się dowodem twierdzenia 24: powierzchni PQR będzie powierzchnia
każdego z trójkątów zbudowanych w analogiczny sposób na bokach PR i RQ (a zatem
ich łączna powierzchnia wynosi 1/16 powierzchni PQq). I tak dalej w
nieskończoność. Tym razem Archimedes nie konstruuje ciągu trójkątów opisanych na
rozważanej figurze, ale traktuje pole powierzchni segmentu paraboli jako sumę
pól powierzchni trójkątów wpisanych. Aby rozwiązać całe zadanie, pozostaje
policzyć sumę nieskończonego szeregu:
powierzchni PQR będzie powierzchnia
każdego z trójkątów zbudowanych w analogiczny sposób na bokach PR i RQ (a zatem
ich łączna powierzchnia wynosi 1/16 powierzchni PQq). I tak dalej w
nieskończoność. Tym razem Archimedes nie konstruuje ciągu trójkątów opisanych na
rozważanej figurze, ale traktuje pole powierzchni segmentu paraboli jako sumę
pól powierzchni trójkątów wpisanych. Aby rozwiązać całe zadanie, pozostaje
policzyć sumę nieskończonego szeregu: Najsłynniejszym dziełem Eratostenesa było O pomiarze Ziemi,
które znamy dzięki relacjom Strabona z Amazei, i innych. Wiedząc o tym, że w
dniu przesilenia letniego Słońce w Syene (obecnie Asuan nad Nilem) świeci w samo
południe pionowo w górze, Eratostenes zmierzył kąt, pod jakim w tym samym czasie
pada cień w Aleksandrii. Wynosił on 1/50 kąta pełnego. Syene leżało ok. 5000
stadiów na południe od ujścia Nilu. Na podstawie pomiarów odległości Słońca,
dokonanych kilkadziesiąt lat wcześniej przez Arystarcha, Eratostenes mógł
przyjąć, że z bardzo dobrym przybliżeniem promienie słoneczne w obu miastach są
równoległe.
Najsłynniejszym dziełem Eratostenesa było O pomiarze Ziemi,
które znamy dzięki relacjom Strabona z Amazei, i innych. Wiedząc o tym, że w
dniu przesilenia letniego Słońce w Syene (obecnie Asuan nad Nilem) świeci w samo
południe pionowo w górze, Eratostenes zmierzył kąt, pod jakim w tym samym czasie
pada cień w Aleksandrii. Wynosił on 1/50 kąta pełnego. Syene leżało ok. 5000
stadiów na południe od ujścia Nilu. Na podstawie pomiarów odległości Słońca,
dokonanych kilkadziesiąt lat wcześniej przez Arystarcha, Eratostenes mógł
przyjąć, że z bardzo dobrym przybliżeniem promienie słoneczne w obu miastach są
równoległe. Bardzo ważne miały się okazać jego prace
z zakresu astronomii – które wówczas zaliczano do matematyki – poświęcone
ruchowi Słońca. Jeśli dokładnie wyznaczymy dni, w których Słońce wschodzi i
zachodzi najdalej na północ (tego dnia zaczyna się lato), w których wschodzi i
zachodzi po przeciwległych krańcach horyzontu (są to pierwsze dni wiosny i
jesieni), a wreszcie kiedy wschodzi i zachodzi najdalej na południu (i zaczyna
się zima), to okaże się, że długości pór roku nie są takie same. Dokładniejsze
dane uzyskamy wyznaczając drogę Słońca na tle gwiazd i ustalając, kiedy wchodzi
ono w kolejne znaki zodiaku. Wiosna trwa 92 ¾ dnia, lato 93 ¾ dnia, jesień 89 ¾
dnia, a zima 89 dni. Dla pitagorejczyka bądź platonika jest to spostrzeżenie
bardzo niemiłe, uważali oni bowiem, że ciałom niebieskim przystoją tylko ruchy
doskonałe. Apollonios znalazł rozwiązanie zgodne z pitagorejsko-platońskimi
ideałami: Słońce, wirując ruchem dobowym wraz z gwiazdami, porusza się też w
stosunku do gwiazd „doskonałym” ruchem jednostajnym po okręgu, tyle
Bardzo ważne miały się okazać jego prace
z zakresu astronomii – które wówczas zaliczano do matematyki – poświęcone
ruchowi Słońca. Jeśli dokładnie wyznaczymy dni, w których Słońce wschodzi i
zachodzi najdalej na północ (tego dnia zaczyna się lato), w których wschodzi i
zachodzi po przeciwległych krańcach horyzontu (są to pierwsze dni wiosny i
jesieni), a wreszcie kiedy wschodzi i zachodzi najdalej na południu (i zaczyna
się zima), to okaże się, że długości pór roku nie są takie same. Dokładniejsze
dane uzyskamy wyznaczając drogę Słońca na tle gwiazd i ustalając, kiedy wchodzi
ono w kolejne znaki zodiaku. Wiosna trwa 92 ¾ dnia, lato 93 ¾ dnia, jesień 89 ¾
dnia, a zima 89 dni. Dla pitagorejczyka bądź platonika jest to spostrzeżenie
bardzo niemiłe, uważali oni bowiem, że ciałom niebieskim przystoją tylko ruchy
doskonałe. Apollonios znalazł rozwiązanie zgodne z pitagorejsko-platońskimi
ideałami: Słońce, wirując ruchem dobowym wraz z gwiazdami, porusza się też w
stosunku do gwiazd „doskonałym” ruchem jednostajnym po okręgu, tyle że środek
okręgu nie znajduje się w środku Ziemi. Skoro spoglądamy na Słońce spoza środka
jego orbity, to zdaje się nam, że w porusza się ono na tle gwiazd raz szybciej a
raz wolniej – co pociąga za sobą różną długość pór roku.
że środek
okręgu nie znajduje się w środku Ziemi. Skoro spoglądamy na Słońce spoza środka
jego orbity, to zdaje się nam, że w porusza się ono na tle gwiazd raz szybciej a
raz wolniej – co pociąga za sobą różną długość pór roku.