DZIEJE RELIGII, FILOZOFII I NAUKI
indeks |
antologia religijna |
antologia filozoficzna |
filozofia nauki
Wojciech Sady: wykłady
Wojciech Sady
Początki astronomii matematycznej
z: Dzieje religii, filozofii i nauki: od Talesa z Miletu
do Mahometa, Marek Derewiecki 2010
1. Co widać na niebie?
2. Matematyczny model ruchów gwiazd i planet Eudoksosa
3. Heraklides z Pontu o wirowym ruchu Ziemi
1. Co widać na niebie?
Połowa tego, co widzimy spacerując po otwartym polu, to rzeczy tej ziemi, druga
połowa to niebo. Na niebie widać ptaki, chmury, czasem błyskawicę lub zorzę
polarną – a ponad chmurami to, co nazywamy ciałami niebieskimi.
W pogodny dzień na błękitnym tle świeci Słońce, odbywające wędrówkę ze wschodu na
zachód. Latem wędruje wyżej i świeci na niebie dłużej niż zimą. Są dwa dni w
roku (20 marca i 23 września), kiedy Słońce wschodzi prawie dokładnie na
wschodzie, a zachodzi prawie dokładnie na zachodzie i pozostaje nad naszymi
głowami przez mniej więcej dwanaście godzin. Nazywamy je dniami przesilenia
wiosennego i przesilenia jesiennego. (Warto w tym miejscu podkreślić – o czym
będzie dokładniej w § VI.7 – że czas, jaki upływa między przesileniem wiosennym
a jesiennym jest o sześć dni dłuższy niż odstęp między tymi dniami przypadający
na okres zimowy.) 21/22 grudnia, w dniu przesilenia zimowego, dzień jest
najkrótszy, a Słońce wschodzi i zachodzi w punktach wysuniętych najdalej na
południe. 21 czerwca, gdy następuje przesilenie letnie, dzień trwa najdłużej, a
miejsca wschodu i zachodu Słońca są ulokowane najdalej na północ.
O wiele więcej i ciekawszych obiektów widać w nocy, gdy niebo staje się czarne i
ukazują się na nim (mowa o obserwacji gołym okiem) tysiące gwiazd, blada
poświata zwana Drogą Mleczną, Księżyc, planety, a sporadycznie kometa.
Świat gwiazd uderza nas swą odmiennością
od świata ziemskiego: podczas gdy rzeczy w naszym otoczeniu wciąż powstają,
zmieniają się i giną, to gwiazdy – przynajmniej w trakcie naszego życia – świecą
tak samo jasno i są tak samo rozmieszczone względem siebie. Ciała ziemskie
wykonują ruchy najróżniejszych rodzajów, gwiazdy poruszają się tylko w jeden
sposób: biegną ze stałą prędkością, w kierunku przeciwnym do ruchu wskazówek
zegara, po okręgach, których wspólny środek znajduje się nieopodal Gwiazdy
Północnej, zwanej też Polarną. Jest to dość jasna gwiazda, która przez całą noc
i przez cały rok świeci mniej więcej w tym samym miejscu; z Polski widać ją pod
kątem pięćdziesięciu paru stopni ponad horyzontem. (Gdy wyprostujemy rękę i
maksymalnie rozsuniemy palce, kąt, którego wierzchołek stanowi nasze oko, a
ramiona przechodzą przez czubki kciuka i małego palca, wynosi około 200).
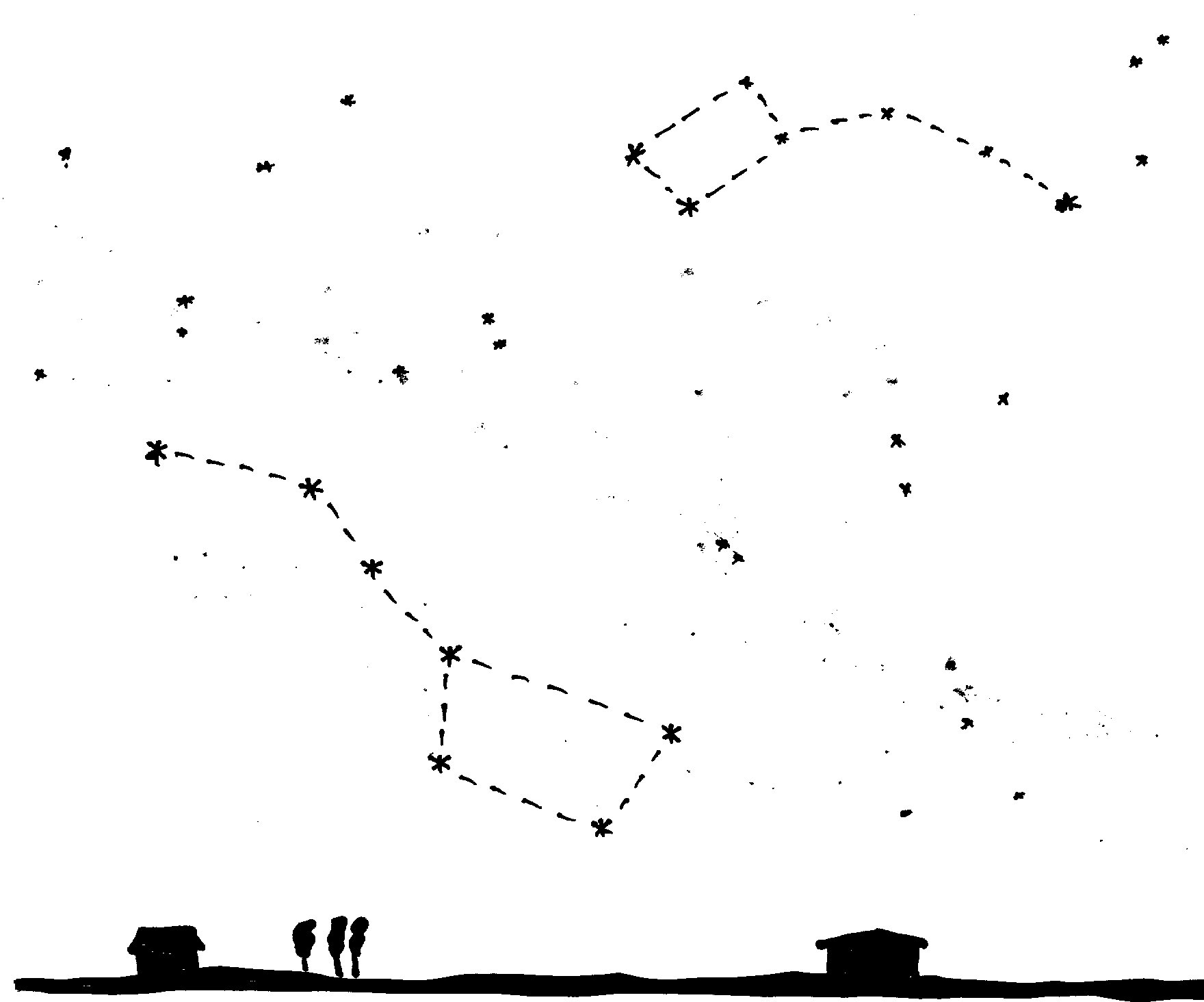 Jeśli będziemy przyglądać się gwiezdnemu
niebu przez okrągły rok, zauważymy ciekawe zjawisko. Skupmy uwagę na siedmiu
jasnych gwiazdach, tworzących układ zwany Wielkim Wozem lub Wielką
Niedźwiedzicą. Jesienią, gdy zapada zmrok, gwiazdozbiór ten ukazuje się
pod Gwiazdą Północną (jak na zamieszczonym rysunku); po sześciu godzinach
widać go na prawo od niej, a po dwunastu
ponad nią, prawie nad naszymi głowami. Potem zaczyna się kolejny dzień i gwiazdy
nikną, kontynuują jednak swoją wędrówkę i następnego wieczora Wielki Wóz znów
świeci pod Gwiazdą Północną – dociera jednak w to samo miejsce, w którym był
poprzedniej nocy, prawie cztery minuty wcześniej. W ciągu tych czterech minut
obraca się, wraz z całym gwiezdnym niebem, o niemal jeden stopień. W rezultacie
z nocy na noc ukazuje się coraz dalej – licząc w kierunku przeciwnym do ruchu
wskazówek zegara – i zimą, o tej samej godzinie co jesienią, widać go
na prawo od Gwiazdy Północnej, wiosną wieczorem świeci ponad
nią, a latem na lewo od niej. (Tekst ten, nieco zawiły, stanie się jasny dla każdego, kto popatrzy na
nocne niebo miesiąc po miesiącu o różnych godzinach).
Jeśli będziemy przyglądać się gwiezdnemu
niebu przez okrągły rok, zauważymy ciekawe zjawisko. Skupmy uwagę na siedmiu
jasnych gwiazdach, tworzących układ zwany Wielkim Wozem lub Wielką
Niedźwiedzicą. Jesienią, gdy zapada zmrok, gwiazdozbiór ten ukazuje się
pod Gwiazdą Północną (jak na zamieszczonym rysunku); po sześciu godzinach
widać go na prawo od niej, a po dwunastu
ponad nią, prawie nad naszymi głowami. Potem zaczyna się kolejny dzień i gwiazdy
nikną, kontynuują jednak swoją wędrówkę i następnego wieczora Wielki Wóz znów
świeci pod Gwiazdą Północną – dociera jednak w to samo miejsce, w którym był
poprzedniej nocy, prawie cztery minuty wcześniej. W ciągu tych czterech minut
obraca się, wraz z całym gwiezdnym niebem, o niemal jeden stopień. W rezultacie
z nocy na noc ukazuje się coraz dalej – licząc w kierunku przeciwnym do ruchu
wskazówek zegara – i zimą, o tej samej godzinie co jesienią, widać go
na prawo od Gwiazdy Północnej, wiosną wieczorem świeci ponad
nią, a latem na lewo od niej. (Tekst ten, nieco zawiły, stanie się jasny dla każdego, kto popatrzy na
nocne niebo miesiąc po miesiącu o różnych godzinach).
Tak więc gwiazdy obracają się nad naszymi
głowami nieco szybciej niż Słońce: w ciągu roku wykonują o jeden obrót więcej.
Gdybyśmy mogli widzieć Słońce wraz z gwiezdnym niebem, obserwowalibyśmy, jak z
dnia na dzień przesuwa się ono na tle gwiazd o około 10
(czyli o dwie swoje średnice), z nieco
różną prędkością w różnych miesiącach. Gwiazdy otaczające Gwiazdę Północną widać
przez całą noc i o każdej porze roku. Natomiast te świecące po tej stronie
nieba, po której wędruje Słońce, nieustannie wynurzają się znad wschodniego
horyzontu, podczas gdy inne kryją się za horyzontem na zachodzie. Jeśli o
północy spojrzymy prosto na południe, to na odpowiedniej wysokości (wyżej zimą
niż latem) ujrzymy gwiazdy, na których tle znajdzie się Słońce za pół roku –
tyle że one wtedy będą niewidoczne.
Drogę Słońca na tle gwiazd
zrekonstruowali jako pierwsi mezopotamscy uczeni, zwani Chaldejczykami, a stało
się to przed 1000 r. p.n.e. Bardzo ich ruch Słońca interesował, bowiem uprawiali
(a może od podstaw stworzyli) dyscyplinę zwaną astrologią.
Astrologia jest sposobem przewidywania przyszłości na podstawie tego, co widać
na niebie. Jej zwolennicy są przekonani, że charakter i los człowieka są
wyznaczone przez to, w jakim miejscu znajdowały się ciała niebieskie w chwili
jego narodzin. Aby te miejsca określić, podzielono drogę Słońca na tle gwiazd na
dwanaście równych części. (12 jako podzielne przez 2, 3 i 4, oraz 60 jako
podzielne przez 2, 3, 4 i 5, odgrywały szczególną rolę w chaldejskiej
matematyce. Podziały te, po upływie 3000 lat, wciąż widać na tarczach naszych
zegarów.) Używane dziś nazwy tych rejonów nieba: Wodnik, Ryby, Baran, Byk,
Bliźnięta, Rak, Lew, Panna, Waga, Skorpion, Strzelec, Koziorożec, częściowo
odpowiadają starożytnym. Jeśli na gwiezdnym niebie nakreślimy okrąg prostopadły
do kierunku, w jakim znajduje się Gwiazda Północna, to droga Słońca będzie
nachylona do niego pod kątem 23½0;
oba okręgi przetną się w miejscach, gdzie Ryby stykają się z Baranem, a Panna z
Wagą.
Dwanaście znaków zodiaku i jedno Słońce to stanowczo za mało: mielibyśmy wtedy
tylko dwanaście rodzajów ludzkich losów. Astrolodzy dodają jednak do tego sześć
obiektów widocznych na nocnym niebie i, podobnie jak Słońce, wędrujących na tle
gwiazd.
Średnio raz na 29,5 dnia Księżyc ukazuje
się wieczorem w nowiu, jako wąski sierp, nisko nad horyzontem, nieco na lewo od
miejsca, gdzie zaszło Słońce; po jakiejś godzinie zachodzi. Następnego wieczora
jest grubszy, ukazuje się o ok. 120
wyżej i prawie godzinę dłużej świeci nim skryje się za horyzontem. Przez dwa
tygodnie powtarza się to samo: rośnie, a wieczorem zaczyna świecić coraz dalej
na wschód. Wreszcie osiąga pełnię, gdy wieczorem wynurza się na wschodzie,
akurat wtedy, gdy Słońce zachodzi po przeciwnej stronie horyzontu (mowa o
okresach wiosennych i jesiennych, zimą i latem trzeba wziąć poprawkę na to, że
dzień trwa krócej lub dłużej niż noc). Księżyc w pełni świeci przez całą noc,
wraz z gwiazdami wędrując ze wschodu na zachód. A potem z nocy na noc zaczyna
wynurzać się zza wschodniego horyzontu coraz później i jest go coraz mniej, aż
po kolejnych dwóch tygodniach wyłania się na wschodzie nad ranem jako wąski
sierp, by szybko niknąć w promieniach wschodzącego Słońca. Przez dwie lub trzy
noce nie widać go wcale, po czym znów ukazuje się w nowiu.
Księżyc, podobnie jak Słońce, wędruje ze
wschodu na zachód nieco wolniej niż gwiazdy, w rezultacie na tle gwiazd przesuwa
się powoli, po drodze mniej więcej tej samej co Słońce, schodząc z niej jednak
raz w górę a raz w dół o kilka stopni. (Kątowa średnica tarcz Słońca i Księżyca
wynosi około pół stopnia.) Przebiega wszystkie znaki zodiaku średnio w ciągu
27,3 dnia, a zatem przemieszcza się z jednego znaku do drugiego co nieco ponad
dwie doby. Jednak w poszczególnych fazach szybkość jego ruchu na tle gwiazd
zmienia się, od 11,70
do 14,60
na dobę, a dodatkowo w kolejnych cyklach czas, w jakim Księżyc obiega dwanaście
znaków zodiaku, różni się do 7 godzin.
Wzdłuż drogi, którą na tle gwiazd wędruje
Słońce, można dostrzec nocą jeszcze pięć jasnych punktów, zwanych Merkury,
Wenus, Mars, Jowisz i Saturn. One również przemieszczają się powoli na tle
gwiazd „stałych”. (Używane do XVII w. określenie „gwiazdy stałe” miało
podkreślać, że obracając się nad naszymi głowami nie zmieniają one swych położeń
względem siebie.) Od greckiego planao,
„wędrować”, nazwano je, wraz ze Słońcem i Księżycem, planetami. (Starożytność
znała więc siedem planet, dziś na ich liście są o dwa obiekty mniej, a zarazem o
trzy więcej. Dalej planetami będę nazywał pięć obiektów wymienionych przed
chwilą.) Planety różni od gwiazd stałych także to, że w pewnych okresach świecą
silniej, a w pewnych słabiej. (W pogodną noc uważny obserwator dostrzeże
ponadto, że światło gwiazd mruga, a planet nie).
Planety wędrują na tle gwiazd inaczej niż Słońce i Księżyc. Te dwa ciała zawsze
pozostają z tyłu za gwiazdami, z planetami najczęściej dzieje się to samo,
jednak niekiedy poruszają się przez pewien czas ze wschodu na zachód troszkę
szybciej niż gwiazdy. Wykonują wtedy na tle gwiazd ruchy zwane „wstecznymi”. Tu
trzeba rozbić opis na dwie części.
„Planety górne”, czyli Mars, Jowisz i Saturn, wykonują ruchy wsteczne wtedy, gdy
wieczorem ukazują się w przybliżeniu na wschodzie i przez prawie całą noc widać
je, jak podążają wraz z gwiazdami stałymi na zachód. A zatem, gdy znajdują się
po przeciwległej stronie nieba niż Słońce. Świecą też wtedy najjaśniej (w
przypadkach Marsa i Jowisza jaśniej niż jakakolwiek z gwiazd). W rezultacie na
tle gwiazd kreślą drogi, na których występują pętle.
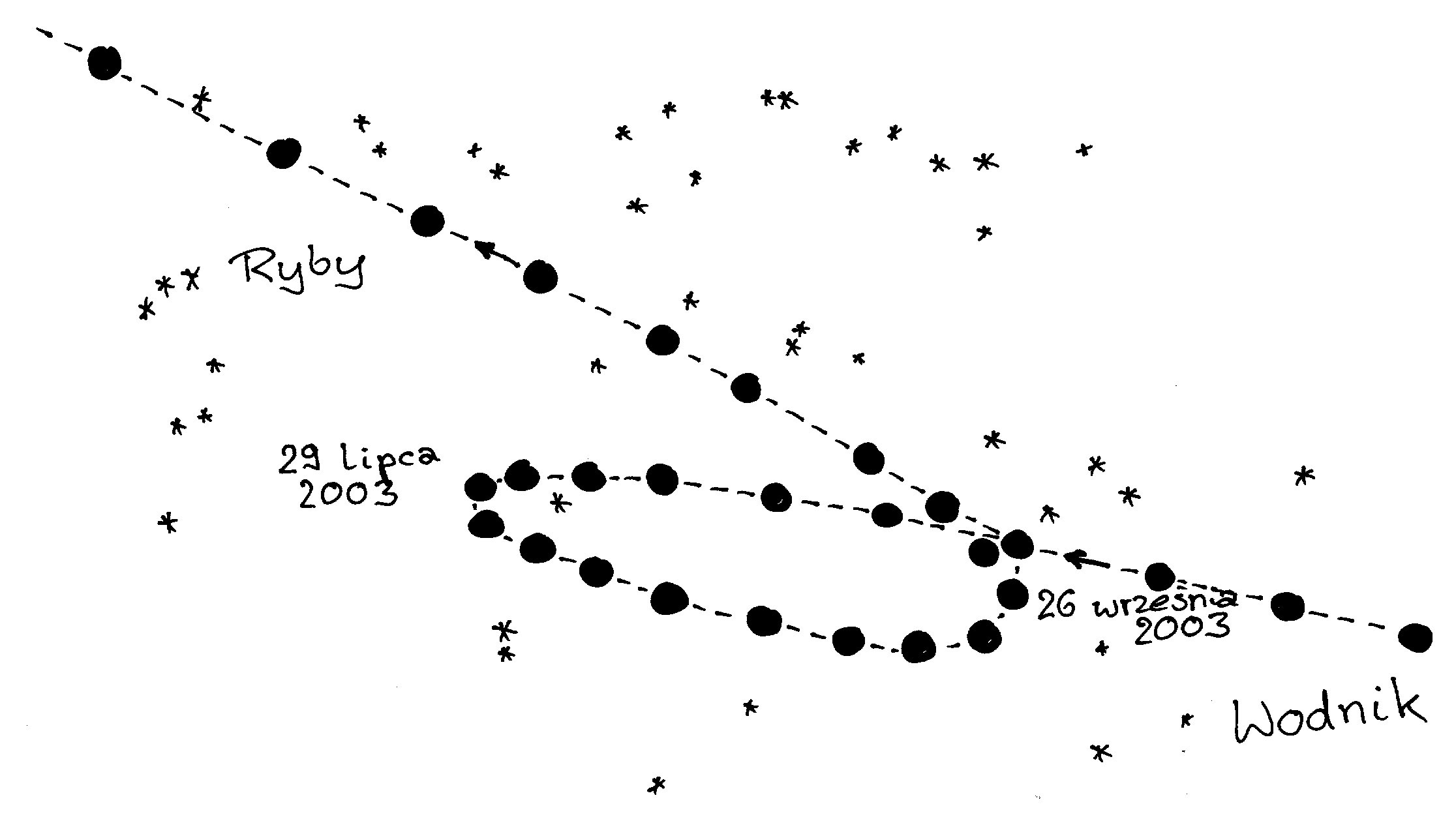 Szczególnie w przypadku Marsa zjawisko to
jest jednak dość nieregularne. Zajrzyjmy do danych nam współczesnych. Zaczynając
od 2001 r. kolejne okresy ruchu wstecznego dzieliło i będzie (pisane w 2007 r.)
dzielić 806, 812, 767, 767 i 783 dni (w długim okresie średni odstęp – tzw.
okres synodyczny – wynosi 780 dni). W tych okresach przemieści się on na tle
gwiazd ze wschodu na zachód o ok. 720, 700, 470,
370 i 340(wieloletnia średnia wynosi 480).
Ruch wsteczny trwa od ok. 8 do 11 tygodni. (Na rysunku przedstawiono położenia
Marsa na tle gwiazd odnotowywane w odstępach mniej więcej sześciodniowych w 2003
r.)
Szczególnie w przypadku Marsa zjawisko to
jest jednak dość nieregularne. Zajrzyjmy do danych nam współczesnych. Zaczynając
od 2001 r. kolejne okresy ruchu wstecznego dzieliło i będzie (pisane w 2007 r.)
dzielić 806, 812, 767, 767 i 783 dni (w długim okresie średni odstęp – tzw.
okres synodyczny – wynosi 780 dni). W tych okresach przemieści się on na tle
gwiazd ze wschodu na zachód o ok. 720, 700, 470,
370 i 340(wieloletnia średnia wynosi 480).
Ruch wsteczny trwa od ok. 8 do 11 tygodni. (Na rysunku przedstawiono położenia
Marsa na tle gwiazd odnotowywane w odstępach mniej więcej sześciodniowych w 2003
r.)
W dłuższych okresach czasu odkrywamy
jednak pewną regularność. Oto zanim zacznie się kolejny ruch wsteczny
Mars przebiega, z zachodu na wschód, wszystkie dwanaście znaków Zodiaku
i jeszcze parę, tak że następna pętla wypada dalej na wschód średnio o 550.
A zatem co mniej więcej 15 lat planeta wykonuje swoje ruchy wsteczne w tym samym
rejonie nieba, te zaś pętle są do siebie podobne i następują po sobie w
podobnych okresach.
Jowisz, dla którego okres synodyczny
wynosi 399 dni, na obiegnięcie dwunastu znaków Zodiaku ruchem na przemian z
zachodu na wschód, a krócej ze wschodu na zachód, potrzebuje około 12 lat.
Ruchy wsteczne Saturna trwają około 4,5
miesiąca, a następują po sobie średnio co 378 dni. Planeta ta przebiega
wszystkie znaki zodiaku w ciągu około 29,5 roku. (Jeśli więc ktoś żyje
sześćdziesiąt lat, to Saturn w tym czasie dwukrotnie powraca w ten rejon
nieba, w którym świecił, gdy człowiek ów przychodził na świat).
Merkury i Wenus to „planety dolne”,
charakteryzujące się tym, że nigdy nie oddalają się zbytnio od Słońca. Ukazują
się zatem czasem na zachodnim niebie, gdy tylko zapada mrok, a wkrótce potem,
podążając za gwiazdami, kryją się za horyzontem. W innych okresach wyłaniają się
zza wschodniego horyzontu krótko przed świtem, wznoszą się w górę, aby zniknąć
gdy niebo się rozjaśnia. Ponieważ towarzyszą Słońcu, to przebiegają wszystkie
znaki zodiaku średnio w ciągu roku.
Raz na ok. rok i siedem miesięcy (średnio
584 dni) Wenus ukazuje się wieczorem na zachodzie, na lewo od miejsca gdzie
zaszło Słońce – i szybko niknie za horyzontem. Z nocy na noc ukazuje się coraz
wyżej, widoczna jest więc na niebie coraz dłużej, a jej jasność wciąż rośnie.
Ale nigdy nie oddala się od Słońca więcej niż o 470
(zachodzi wtedy po mniej więcej trzech
godzinach). W okresie tego największego oddalenia jest najjaśniejszym po
Księżycu obiektem na nocnym niebie. Potem następuje okres, gdy z wieczora na
wieczór zaczyna być widoczna wciąż niżej, świeci więc coraz krócej, a od pewnego
dnia jej jasność przygasa. Aż wreszcie znika. Czas jakiś pozostaje niewidoczna,
po czym zaczyna wyłaniać się znad wschodniego horyzontu przed świtem, wznosi się
w górę – i niknie w promieniach wschodzącego Słońca. (Najwcześniejsze odkryte w
Mezopotamii tabliczki gliniane z zapiskami dotyczącymi pojawiania się „Gwiazdy
Wieczornej”, a w pewien czas po niej „Gwiazdy Porannej”, pochodzą w początków II
tysiąclecia p.n.e.)
Merkury pojawia się na zachodnim niebie
zaraz po zmroku raz na niecałe cztery miesiące (średnio 116 dni) i zachowuje się
analogicznie jak Wenus. Ale oddala się od Słońca o najwyżej 280,
a świeci dość słabo, tak że dostrzeżenie go – zwłaszcza z Polski, gdzie niebo
nad horyzontem jest najczęściej zamglone – nie jest łatwe.
Siedem planet, z których każda może
znajdować się w jednym z dwunastu znaków zodiaku – to daje 127,
czyli ok. 35 milionów możliwości. Astrologiczne horoskopy mogą więc być ogromnie
zróżnicowane. Nas jednak interesuje teraz, co z danymi astronomicznymi zrobili
uczeni greccy, inspirowani pitagorejską wiarą w matematyczne harmonie rządzące
kosmosem. Zaczęło się od spekulacji, w których dane ilościowe dotyczące ruchów
ciał niebieskich odgrywały, jak się wydaje, niewielką rolę.
2. Matematyczny model ruchów gwiazd i planet Eudoksosa
Eudoksos z Knidos
(408-355 p.n.e.) podczas pobytu w Italii był uczniem pitagorejczyka Archytasa z
Tarentu, w Akademii słuchał wykładów Platona, studiował astronomię w Egipcie, a
wreszcie w rodzinnym mieście założył własną szkołę. Po raz drugi przybył do Aten
w otoczeniu uczniów w 368 r. p.n.e. Platon, który wcześniej, w zakończeniu
Państwa, kazał trzem boginiom odpowiednio spowalniać i przyspieszać obroty
„mis” planetarnych, pod wrażeniem systemu Eudoksosa w swym ostatnim tekście
zapisał:
Zacni mężowie, oto
my wszyscy Grecy, rzec można, wypowiadamy teraz zupełne kłamstwa o potężnych
bóstwach, o Heliosie [Słońcu] i o Selenie [Księżycu]. (...) Twierdzimy, że nigdy
nie odbywają tej samej drogi i wraz z nimi jeszcze inne ciała niebieskie, które
też z tego powodu nazywamy błądzącymi gwiazdami. (...) ja sam bynajmniej już nie
w młodym wieku zdobyłem te wiadomości (...). Nie jest, widzicie, zgodny z prawdą
pogląd, że Słońce, Księżyc i inne ciała wędrują wciąż po innych drogach, lecz
jest zupełnie przeciwnie – tą samą bowiem każde ciało niebieskie przemierza
zawsze drogę (...). [Prawa 821B-822A]
Ale jakie stosunki wiązały oby
myślicieli, i czy jeden drugiego inspirował, nie wiemy. Po powrocie w rodzinne
strony Eudoksos zbudował obserwatorium astronomiczne, żadne z dostępnych źródeł
nie świadczy jednak o tym, aby dokonywano tam obserwacji innych niż tylko
jakościowe.
Wszystkie dzieła Eudoksosa zaginęły. Jego
dokonania w zakresie matematyki znamy dzięki relacjom Euklidesa i Archimedesa.
Zaś zbudowany przezeń system astronomiczny zrekonstruowano na podstawie uwag
współczesnego mu Arystotelesa i żyjącego dziewięć wieków później Simplikiosa.
Jako matematyk, Eudoksos miał rozwinąć
metodę „wyczerpywania” (zob. § VI.5) i stosując ją udowodnić – znane wcześniej –
twierdzenia, że objętość piramidy jest równa jednej trzeciej objętości
prostopadłościanu o takiej samej podstawie i wysokości, oraz że taki sam
stosunek zachodzi dla stożka i walca.
Wniósł też wkład do
matematycznej teorii proporcji, a szereg jego wyników w tym zakresie zawiera V
księga Elementów (Definicja 4 nosi tam nazwę Aksjomatu Eudoksosa).
Ogromnie ważne były
jego prace na temat liczb niewymiernych. (Dedekind podkreślał, że jego słynna
praca o „cięciach” z 1872 r. była inspirowana ideami Eudoksosa.) Odkrycie takich
liczb stanowiło dla pitagorejczyków prawdziwy szok – ich „boski” nauczyciel
głosił przecież, że wszystko da się sprowadzić do liczb naturalnych i ich
stosunków. Eudoksos pokazał natomiast,
że można porównywać stosunki dowolnych liczb, zarówno wymiernych, jak i
niewymiernych. We współczesnej notacji (uniknę przytaczania trudno dziś
zrozumiałej Definicji 5 z V księgi Elementów), a : b = c
: d, jeśli dla dowolnej pary liczb całkowitych m i n
(1) jeśli ma < nb, to mc < nd,
(2) jeśli ma = nb, to mc = nd,
(3) jeśli ma > nb, to mc > nd.
W ten sposób liczby niewymierne zostały
wprowadzone do matematyki: można było nimi odtąd operować podobnie jak
„zwykłymi” ułamkami.
Ale Eudoksos słynie przede wszystkim jako
autor pierwszego w dziejach systemu astronomii matematycznej. Dlaczego i jak
mogło dojść do jego skonstruowania? Jako pitagorejczyk, szukał on matematycznych
harmonii kryjących się za zjawiskami. Obserwowano, że gwiazdy poruszają się nad
naszymi głowami ruchami jednostajnymi po okręgach. Okrąg jest jedyną (obok linii
prostej) figurą, na której nie ma punktów wyróżnionych, a skoro prędkość się nie
zmienia, to każda faza gwiezdnego ruchu jest identyczna z każdą inną. Gwiezdne
niebo jawiło się, z pitagorejskiego punktu widzenia, jako doskonałe: nic tam nie
powstaje i nie ginie, a jego obrót jest żywym obrazem wieczności. Widok planet
zaburzał, na pierwszy rzut oka, przekonanie o niebiańskim ładzie. Słońce i
Księżyc nie tylko poruszają się wolniej niż gwiazdy, ale szybkości ich ruchów
zmieniają się. Z pięcioma pozostałymi planetami jest jeszcze gorzej: poruszają
się raz wolniej, a raz szybciej niż gwiazdy, kreśląc w dodatku, w okresach
ruchów wstecznych, na tle gwiazd pętle.
Aby usunąć napięcie między przekonaniem o
matematycznej doskonałości nieba a wynikami obserwacji Eudoksos przyjął
założenie, że obserwowany ruch planet jest rezultatem złożenia kilku doskonałych
– kołowych i jednostajnych – ruchów. Jest więc doskonały, choć na taki na
pierwszy rzut oka nie wygląda. A oto podstawowe idee matematycznego modelu.
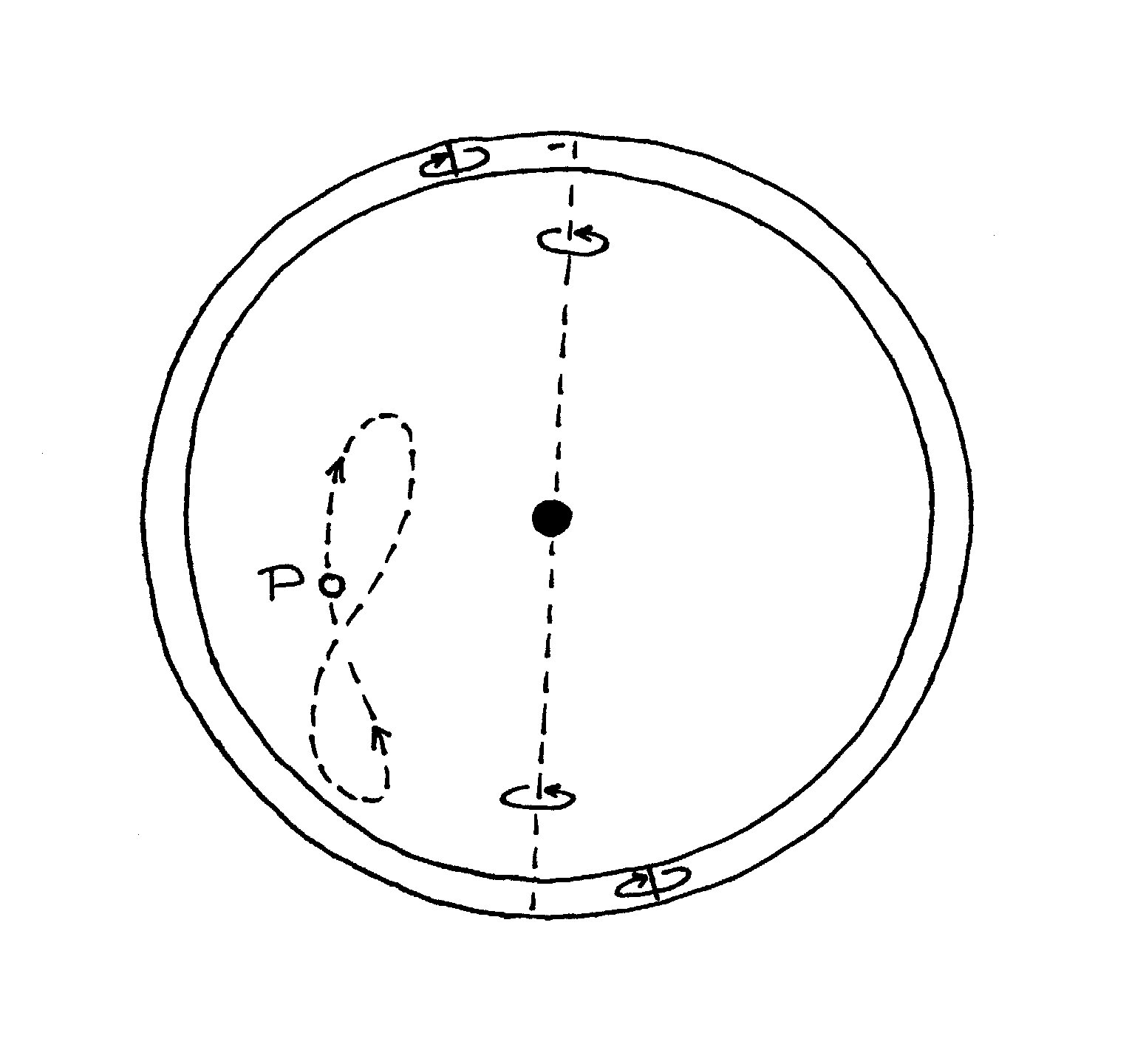
Wyobraźmy sobie wirującą jednostajnie
wokół osi X sferę, na której równiku znajduje się planeta P – będzie ona
poruszała się po okręgu z szybkością jednostajną. A teraz umieśćmy oś tej sfery
w drugiej sferze, która będzie wirować jednostajnie wokół osi Y nachylonej nieco
względem osi sfery pierwszej, z tą samą prędkością kątową, ale w odwrotną
stronę. Ponieważ sfera pierwsza, wirując własnym ruchem, jest zmuszona do
jednoczesnego wirowania ze sferą drugą, to ruch naszego punktu będzie złożeniem
dwóch jednostajnych ruchów po okręgach, nachylonych nieco względem siebie, w
odwrotnych kierunkach. W płaszczyźnie prostopadłej do linii dzielącej na połowę
ostry kąt między osiami obrotu, oba ruchy prawie całkowicie się znoszą, a w
rezultacie punkt na równiku pierwszej sfery wykonuje drgania w górę i w dół.
Ponieważ jedna z płaszczyzn obrotu sama się wraz ze swą sferą obraca, to ruch
wypadkowy naszego punktu będzie przypominał ósemkę (dokładniej jest to tzw.
hipopeda, otrzymywana z przecięcia sfery i cylindra dotykającego sfery od
wewnątrz). A teraz osadźmy oś drugiej sfery w trzeciej sferze, która wiruje
jednostajnie wokół osi Z prostopadłej do płaszczyzny wyznaczonej przez podłużną
oś hipopedy i wspólny środek sfer. Ze złożenia ruchów po ósemce i jednostajnego
ruchu okrężnego otrzymamy krzywą jak na rysunku:
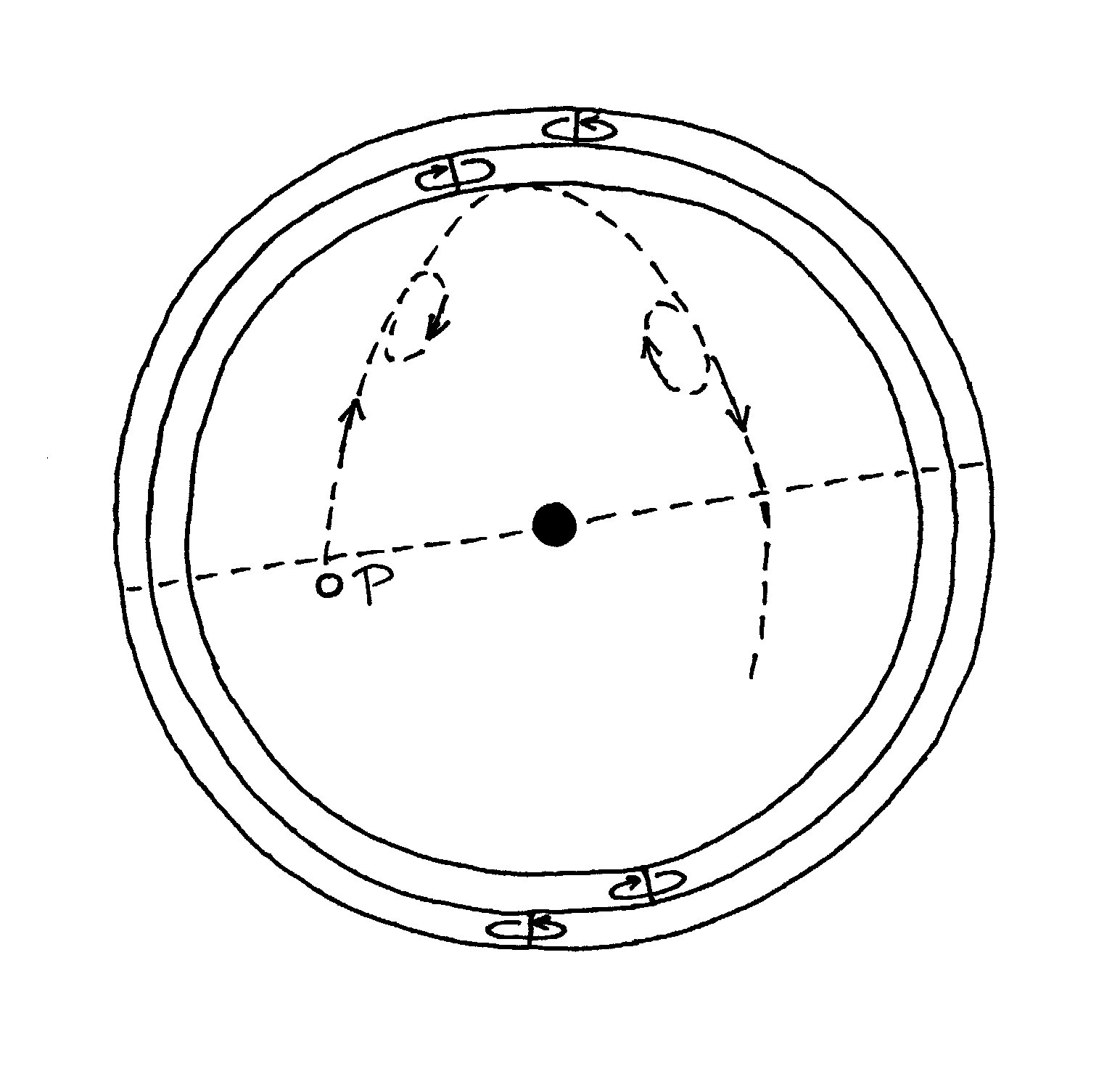 Jakościowo przypomina to znany nam już
ruch planet na tle gwiazd. Łatwo się domyślić – pamiętając o przytoczonych w § 1
wielkościach – że dla Jowisza okres obrotu sfer pierwszej i drugiej powinien
wynosić 399 dni, a okres obrotu sfery trzeciej prawie 12 lat.
Jakościowo przypomina to znany nam już
ruch planet na tle gwiazd. Łatwo się domyślić – pamiętając o przytoczonych w § 1
wielkościach – że dla Jowisza okres obrotu sfer pierwszej i drugiej powinien
wynosić 399 dni, a okres obrotu sfery trzeciej prawie 12 lat.
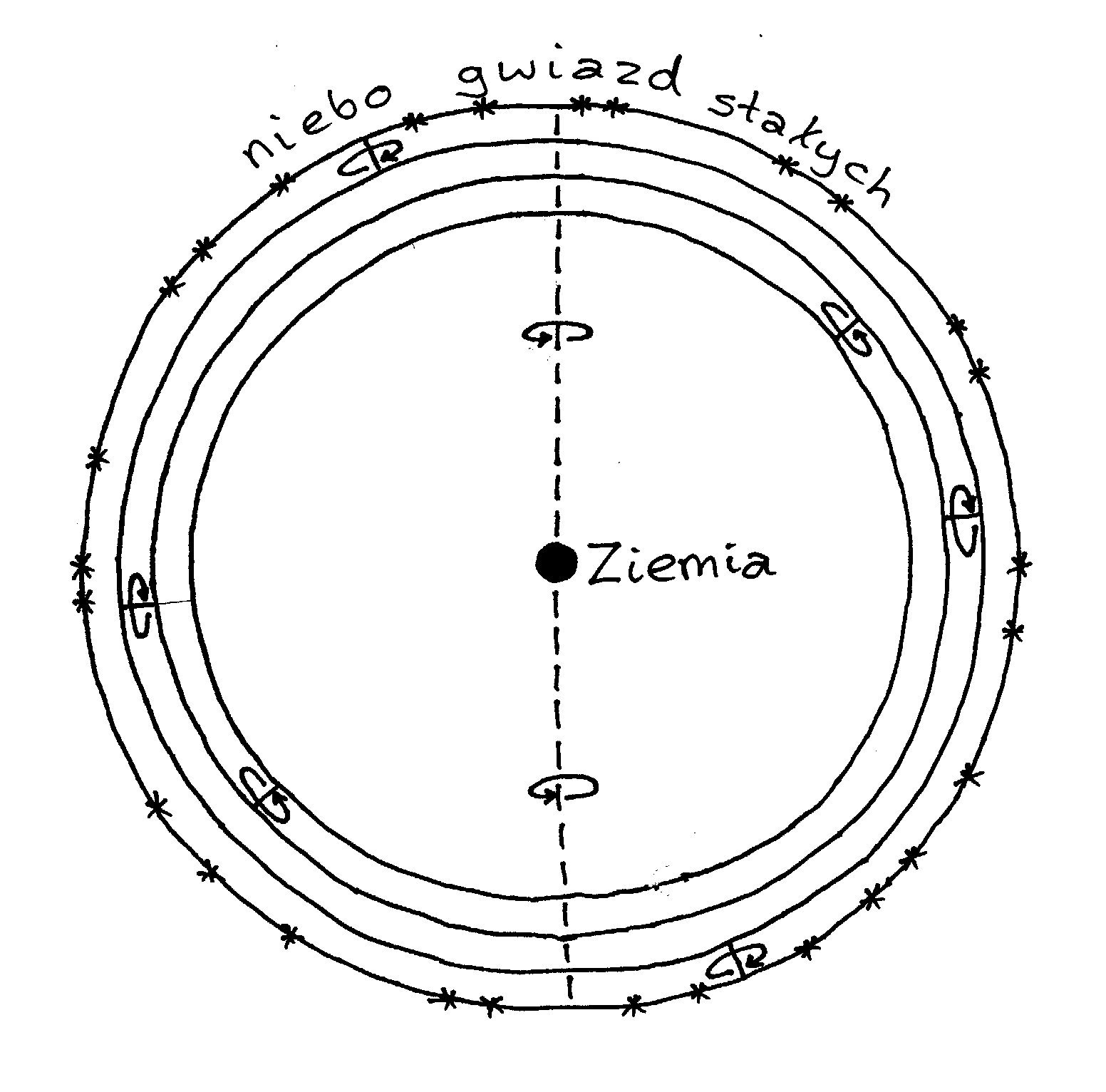 A teraz osadźmy oś
obrotu trzeciej sfery na sferze, której oś G nachylona jest pod kątem 23,50
– tak jak płaszczyzna ekliptyki do równika niebieskiego – do tamtej, tak aby
zmusić trzy wewnętrzne sfery do wirowania wraz ze sferą czwartą i niech ta
ostatnia sfera wykonuje pełny obrót w czasie ok. 23 godzin 56 minut.
A teraz osadźmy oś
obrotu trzeciej sfery na sferze, której oś G nachylona jest pod kątem 23,50
– tak jak płaszczyzna ekliptyki do równika niebieskiego – do tamtej, tak aby
zmusić trzy wewnętrzne sfery do wirowania wraz ze sferą czwartą i niech ta
ostatnia sfera wykonuje pełny obrót w czasie ok. 23 godzin 56 minut.
Jeśli teraz
umieścimy wewnątrz całego układu wirujących sfer Ziemię Z, a na sferze czwartej
ulokujemy gwiazdy, to taki model będzie jakościowo wyjaśniał obserwowane
przez nas zjawiska astronomiczne: dobowy obrót gwiazd „stałych” nad naszą głową,
wraz z planetą, która w ciągu miesięcy i lat wędruje na tle gwiezdnego nieba.
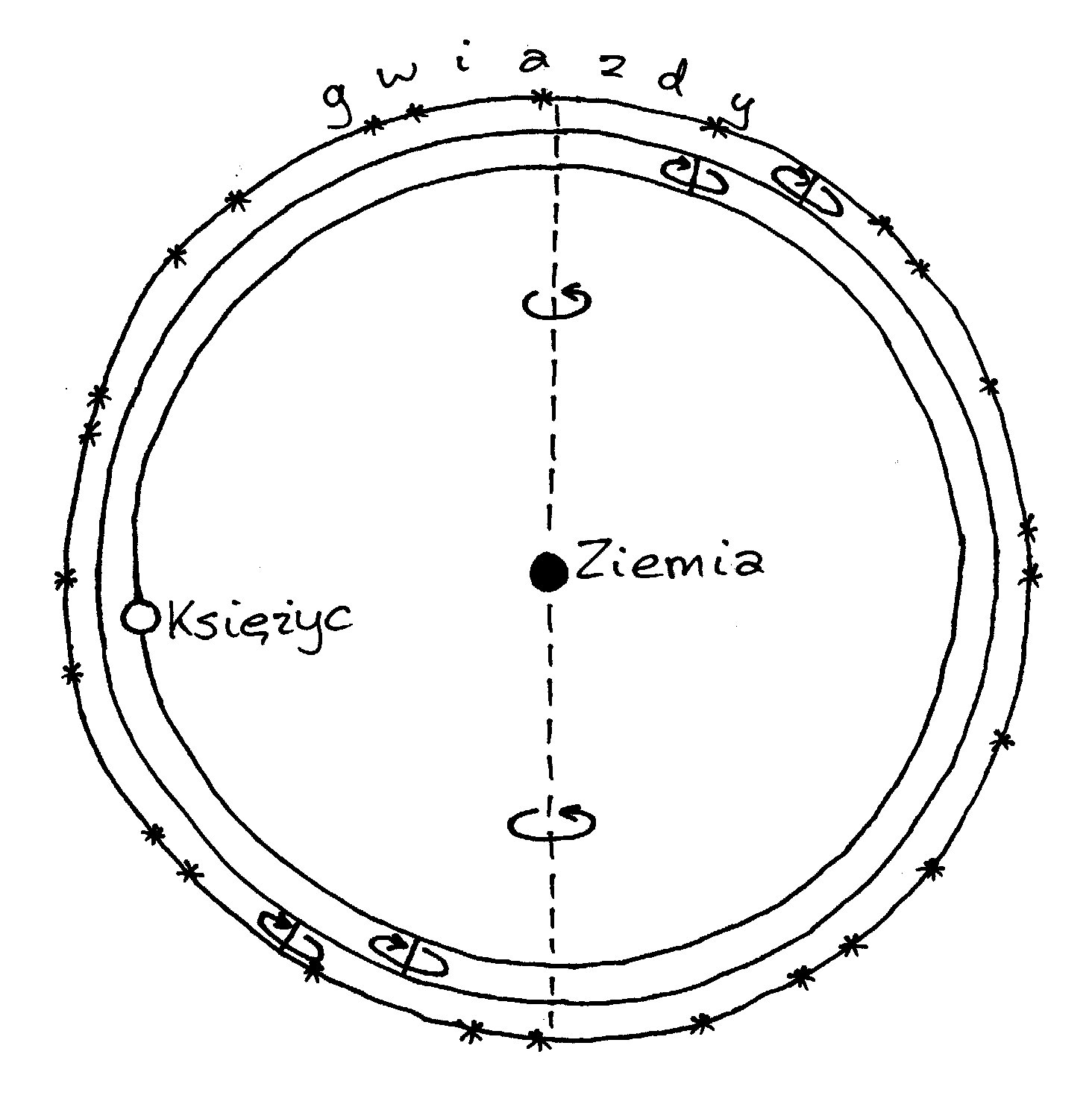
Dla Księżyca model
sfer koncentrycznych Eudoksosa był prostszy, składał się z trzech sfer.
Wewnętrzna wykonywała obrót wokół osi K w czasie ok. 27 1/3 dnia, tłumacząc
wędrówkę Księżyca wzdłuż znaków zodiaku po drodze nachylonej o 50
do płaszczyzny ekliptyki. W płaszczyźnie ekliptyki wirowała wokół osi L sfera
środkowa, a okres jej obrotu, 18,6 lat, odpowiadał odstępom czasu, w jakich
Księżyc, podczas jego zaćmień, znajduje się w tym samym znaku zodiaku.
Zewnętrzną była sfera gwiezdna.
 Dla Słońca Eudoksos również wprowadził
trzy sfery, jednak wyjaśnienie ich roli przez Arystotelesa i Simplikiosa zawiera
niejasności, a nawet błędy.
Dla Słońca Eudoksos również wprowadził
trzy sfery, jednak wyjaśnienie ich roli przez Arystotelesa i Simplikiosa zawiera
niejasności, a nawet błędy.
Model Eudoksosa, choć „doskonały” w
sensie matematycznym, to jedynie jakościowo wyjaśniał ruch Jowisza i Saturna na
tle gwiazd. Dla Marsa i Wenus wymagane przez wyniki obserwacji szybkości obrotów
były takie, że w modelu w ogóle nie powstawał ruch wsteczny. Dlatego pracujący
wraz z Arystotelesem (zob. poniżej) Kallippos z Kyzikos ok. 330 r. p.n.e. dodał
po jednej sferze dla Merkurego, Wenus i Marsa, oraz po dwie dla Słońca i
Księżyca. Powodów wprowadzenia dodatkowych sfer dla trzech planet nie znamy.
Dodatkowe sfery dla Słońca i Księżyca miały wyjaśniać zmiany szybkości ich
ruchów na tle gwiazd.
Zdaje się, że dociekania Eudoksosa i
Kallipposa miały charakter czysto matematyczny. Nie chodziło im o opis
faktycznej budowy nieba, a jedynie o rozwiązanie abstrakcyjnego zagadnienia: jak
przedstawić obserwowalne na niebie ruchy jako wynik złożenia „doskonałych”
ruchów jednostajnych po okręgach. Budowali w tym celu model koncentrycznych
sfer, z których każda – by podsumować powyższe wywody – wirowała z właściwą dla
siebie jednostajną szybkością kątową wokół właściwej dla siebie osi, wirując
jednocześnie wraz ze sferą w stosunku do niej zewnętrzną.
Nawet jako
konstrukcja abstrakcyjna, model Eudoksosa-Kallipposa miał oczywiste wady. Nigdy
nie uzyskano ilościowej zgodności między obserwowanymi położeniami planet na tle
gwiazd a położeniami obliczonymi teoretycznie. A nawet ze zgodnością jakościową
były kłopoty. W starożytności bardziej jeszcze krytykowano model z innego
powodu. Panowało przekonanie, że ciała niebieskie nie ulegają zmianom. Tymczasem
planety świecą raz jaśniej, raz ciemniej, co jest skorelowane z fazami ich
ruchów. W omówionym modelu odległość planet od
Ziemi miała być stała, a zatem ich obserwowana przez nas jasność powinna być
niezmienna. Stała była też w modelu odległość Księżyca od Ziemi, a tymczasem
widoczna średnica jego tarczy w cyklu miesięcznym na przemian rośnie i maleje.
A jednak, o czym przekonamy się poniżej,
model Eudoksosa miał odegrać w dziejach kultury śródziemnomorskiej, a później
europejskiej, olbrzymią rolę.
Jako ciekawostkę można dodać, że Eudoksos napisał też liczącą siedem ksiąg
Podróż po ziemi, w której opisał znane sobie ludy, ich systemy polityczne, historie i zwyczaje.
Ważne były relacje dotyczące Egiptu i panującej tam religii, a także o
stowarzyszeniu pitagorejskim w Italii.
3. Heraklides z Pontu o ruchu wirowym Ziemi
Heraklidesowi z Pontu (387-312 p.n.e.)
powierzono kierowanie Akademią podczas trzeciego pobytu Platona na Sycylii. Po
śmierci Speuzypa w 339 r. p.n.e. ubiegał się o stanowisko scholarchy, a gdy
przegrał z Ksenokratesem, przeniósł się z Aten do rodzinnego Pontu. Miał być
autorem dialogów etycznych, dzieł fizycznych, traktatów o gramatyce, retoryce,
muzyce, prac historycznych. Jego związki z pitagorejską mistyką liczb były
najwyraźniej o wiele mniejsze niż w przypadku Eudoksosa, faktycznie nic nie
wiemy o tym, by miał budować matematyczne modele zjawisk.
Trwałe miejsce w dziejach myśli zapewniła
mu hipoteza astronomiczna, znana na podstawie paru źródeł o różnej
wiarygodności, a przede wszystkim z uwagi Simplikiosa:
Heraklides założył, że Ziemia znajduje się w
środku i obraca się, zaś niebo się nie porusza; sądził też, iż za pomocą tego
założenia można zachować zjawiska. [De caelo 519,9]
A zatem Ziemia, zajmująca środek
kulistego wszechświata, wiruje ruchem dobowym wokół własnej osi (w przeciwną
stronę niż w systemie Eudoksosa miały wirować gwiazdy), natomiast sfera gwiazd
stałych pozostaje nieruchoma. Jest jeszcze jeden pogląd przypisywany
Heraklidesowi, a oparty na uwadze znajdującej się w tekście z V w. n.e.:
Heraklides z Pontu, opisując zarówno koło
Wenus, jak i koło Słońca, i nadając obu kołom jeden środek i jeden średni ruch,
pokazał, jak Wenus jest czasem przed, a czasem za Słońcem. [Kalcidius,
Komentarz do Timajosa Platona]
W połowie XIX w. odczytano to tak, że
Wenus okrąża Słońce, a wraz z nim okrąża Ziemię. Dodano do tego Merkurego i tak
powstał mit, jakoby Heraklides w IV w. p.n.e. głosił pogląd analogiczny z tezami
Tychona Brahe z końca XVI w. (planety poruszają się po okręgach wokół Słońca,
które po okręgu ruchem rocznym porusza się wokół nieruchomej Ziemi). Zdaje się
jednak, że „za” Słońcem znaczyło po prostu, iż Wenus niekiedy ukazuje się na
niebie po zachodzie Słońca, a po kilku miesiącach ukazuje się „przed” jego
wschodem.
deklaracja dostępności
 Jeśli będziemy przyglądać się gwiezdnemu
niebu przez okrągły rok, zauważymy ciekawe zjawisko. Skupmy uwagę na siedmiu
jasnych gwiazdach, tworzących układ zwany Wielkim Wozem lub Wielką
Niedźwiedzicą. Jesienią, gdy zapada zmrok, gwiazdozbiór ten ukazuje się
pod Gwiazdą Północną (jak na zamieszczonym rysunku); po sześciu godzinach
widać go na prawo od niej, a po dwunastu
ponad nią, prawie nad naszymi głowami. Potem zaczyna się kolejny dzień i gwiazdy
nikną, kontynuują jednak swoją wędrówkę i następnego wieczora Wielki Wóz znów
świeci pod Gwiazdą Północną – dociera jednak w to samo miejsce, w którym był
poprzedniej nocy, prawie cztery minuty wcześniej. W ciągu tych czterech minut
obraca się, wraz z całym gwiezdnym niebem, o niemal jeden stopień. W rezultacie
z nocy na noc ukazuje się coraz dalej – licząc w kierunku przeciwnym do ruchu
wskazówek zegara – i zimą, o tej samej godzinie co jesienią, widać go
na prawo od Gwiazdy Północnej, wiosną wieczorem świeci ponad
nią, a latem na lewo od niej. (Tekst ten, nieco zawiły, stanie się jasny dla każdego, kto popatrzy na
nocne niebo miesiąc po miesiącu o różnych godzinach).
Jeśli będziemy przyglądać się gwiezdnemu
niebu przez okrągły rok, zauważymy ciekawe zjawisko. Skupmy uwagę na siedmiu
jasnych gwiazdach, tworzących układ zwany Wielkim Wozem lub Wielką
Niedźwiedzicą. Jesienią, gdy zapada zmrok, gwiazdozbiór ten ukazuje się
pod Gwiazdą Północną (jak na zamieszczonym rysunku); po sześciu godzinach
widać go na prawo od niej, a po dwunastu
ponad nią, prawie nad naszymi głowami. Potem zaczyna się kolejny dzień i gwiazdy
nikną, kontynuują jednak swoją wędrówkę i następnego wieczora Wielki Wóz znów
świeci pod Gwiazdą Północną – dociera jednak w to samo miejsce, w którym był
poprzedniej nocy, prawie cztery minuty wcześniej. W ciągu tych czterech minut
obraca się, wraz z całym gwiezdnym niebem, o niemal jeden stopień. W rezultacie
z nocy na noc ukazuje się coraz dalej – licząc w kierunku przeciwnym do ruchu
wskazówek zegara – i zimą, o tej samej godzinie co jesienią, widać go
na prawo od Gwiazdy Północnej, wiosną wieczorem świeci ponad
nią, a latem na lewo od niej. (Tekst ten, nieco zawiły, stanie się jasny dla każdego, kto popatrzy na
nocne niebo miesiąc po miesiącu o różnych godzinach). Szczególnie w przypadku Marsa zjawisko to
jest jednak dość nieregularne. Zajrzyjmy do danych nam współczesnych. Zaczynając
od 2001 r. kolejne okresy ruchu wstecznego dzieliło i będzie (pisane w 2007 r.)
dzielić 806, 812, 767, 767 i 783 dni (w długim okresie średni odstęp – tzw.
okres synodyczny – wynosi 780 dni). W tych okresach przemieści się on na tle
gwiazd ze wschodu na zachód o ok. 720, 700, 470,
370 i 340(wieloletnia średnia wynosi 480).
Ruch wsteczny trwa od ok. 8 do 11 tygodni. (Na rysunku przedstawiono położenia
Marsa na tle gwiazd odnotowywane w odstępach mniej więcej sześciodniowych w 2003
r.)
Szczególnie w przypadku Marsa zjawisko to
jest jednak dość nieregularne. Zajrzyjmy do danych nam współczesnych. Zaczynając
od 2001 r. kolejne okresy ruchu wstecznego dzieliło i będzie (pisane w 2007 r.)
dzielić 806, 812, 767, 767 i 783 dni (w długim okresie średni odstęp – tzw.
okres synodyczny – wynosi 780 dni). W tych okresach przemieści się on na tle
gwiazd ze wschodu na zachód o ok. 720, 700, 470,
370 i 340(wieloletnia średnia wynosi 480).
Ruch wsteczny trwa od ok. 8 do 11 tygodni. (Na rysunku przedstawiono położenia
Marsa na tle gwiazd odnotowywane w odstępach mniej więcej sześciodniowych w 2003
r.)
 Jakościowo przypomina to znany nam już
ruch planet na tle gwiazd. Łatwo się domyślić – pamiętając o przytoczonych w § 1
wielkościach – że dla Jowisza okres obrotu sfer pierwszej i drugiej powinien
wynosić 399 dni, a okres obrotu sfery trzeciej prawie 12 lat.
Jakościowo przypomina to znany nam już
ruch planet na tle gwiazd. Łatwo się domyślić – pamiętając o przytoczonych w § 1
wielkościach – że dla Jowisza okres obrotu sfer pierwszej i drugiej powinien
wynosić 399 dni, a okres obrotu sfery trzeciej prawie 12 lat. A teraz osadźmy oś
obrotu trzeciej sfery na sferze, której oś G nachylona jest pod kątem 23,50
– tak jak płaszczyzna ekliptyki do równika niebieskiego – do tamtej, tak aby
zmusić trzy wewnętrzne sfery do wirowania wraz ze sferą czwartą i niech ta
ostatnia sfera wykonuje pełny obrót w czasie ok. 23 godzin 56 minut.
A teraz osadźmy oś
obrotu trzeciej sfery na sferze, której oś G nachylona jest pod kątem 23,50
– tak jak płaszczyzna ekliptyki do równika niebieskiego – do tamtej, tak aby
zmusić trzy wewnętrzne sfery do wirowania wraz ze sferą czwartą i niech ta
ostatnia sfera wykonuje pełny obrót w czasie ok. 23 godzin 56 minut. Dla Słońca Eudoksos również wprowadził
trzy sfery, jednak wyjaśnienie ich roli przez Arystotelesa i Simplikiosa zawiera
niejasności, a nawet błędy.
Dla Słońca Eudoksos również wprowadził
trzy sfery, jednak wyjaśnienie ich roli przez Arystotelesa i Simplikiosa zawiera
niejasności, a nawet błędy.