DZIEJE RELIGII, FILOZOFII I NAUKI
indeks |
antologia religijna |
antologia filozoficzna |
filozofia nauki
Wojciech Sady: wykłady
Galileo Galilei
Rozmowy i dowodzenia matematyczne
w zakresie dwóch nowych umiejętności dotyczących
mechaniki i ruchów miejscowych
Discorsi e demostrazioni
matematiche intorno a due nuove scienze attenenti alla Mecanica i
Movimenti Locali (1638)
Przełożył F.K. Wydawnictwo Kasy im.
Mianowskiego, Instytut Popierania Nauki, Warszawa, Pałac Staszica, 1930.
DZIEŃ PIERWSZY
DZIEŃ DRUGI
DZIEŃ TRZECI
O ruchu jednostajnym
DZIEŃ CZWARTY
O ruchu pocisków
DZIEŃ PIERWSZY
Proporcjonalność wielkości i wytrzymałości budowli i maszyn
-
Moc i wytrzymałość belki drewnianej, jednym końcem wpuszczonej w mur -
Olbrzymy w świecie roślinnym i zwierzęcym - Ciekawy wypadek pęknięcia kolumny marmurowej -
Przyczyny spójności cząstek materiału - Tarcie włókien jednych o drugie -
Wytrzymałość lin - Przyrząd do spuszczania się po linie na rękach bez uszkodzenia dłoni -
Przyleganie gładkich tafli objaśniane wstrętem natury do próżni - Próżnia nie wystarcza do objaśnienia spójności -
Pomiar siły próżni - Wysokość podnoszenia wody ze studzien - Wytrzymałość drutu miedzianego na rozciąganie -
Próba objaśnienia spójności nieskończenie małymi próżniami - Kurczenie się liny zmoczonej -
Toczenie wieloboków i kół współśrodkowych po dwóch stycznych równoległych -
Miska i ostrokrąg - Ilości skończone i nieskończone - Niemożność porównań w dziedzinie nieskończoności -
Szeregi liczb kolejnych i kwadratów z tych liczb - Jedność jako liczba nieskończona -
Linia prosta jako koło nieskończone - Jedność, ciecz, proszek -
Zwierciadło palące - Prędkość światła - Podział linii na nieskończenie wiele części -
Zgęszczanie i rozrzedzanie ciał - Cienkość pozłoty na drucie srebrnym -
Powierzchnie walców tej samej objętości - Objętości walców jednakiej powierzchni -
Powierzchnia koła i wieloboku izoperymetrycznego - Koło, wielobok na nim opisany i z nim izoperymetryczny -
Zgęszczanie i rozrzedzanie - Potępienie nauki Arystotelesa o spadku ciał - Unoszenie się ciał w wodzie -
Unoszenie się w wodzie i pływanie zwierząt - Spójność cząstek wody; tworzenie się kropli -
Rozpuszczanie się wina czerwonego w wodzie - Spadek w próżni i w ośrodku opornym -
Ciężar powietrza - Wahadło i jego izochronizm - Szmery przy tarciu -
Opór przy ruchu ciała zależy od jego powierzchni - Ruch jednostajny osiągany w ośrodku opornym -
Spadek po łuku trwa krócej niż po cięciwie - Prawa ruchu wahadła - Rozchodzenie się drgań -
Interwały akustyczne - Zgodność i niezgodność dźwięków
Rozmawiający: SALVIATI, SAGREDO i SIMPLICIO
Rozmowy zaczynają się od rozważań nad wytrzymałością
belek drewnianych, kolumn kamiennych i lin.
Po wstępnych rozważaniach rozmówcy przechodzą do pytania, co naadaje
ciałom spoistość.
(...)
 SALVIATI: Jestem na usługi Waszmościów, jeżeli tylko zdołam sobie
przypomnieć wszystko, czego się nauczyłem od naszego Akademika, który
wiele rozmyślał o tych rzeczach i zawsze na podstawie swojej metody
geometrycznej, tak że nie bez racji możnaby to nazwać nową
umiejętnością. Więc, jakkolwiek niektóre zasady przez innych, a
najpierw przez Arystotelesa były wywiedzione, to jednak tu są
najpiękniejsze i najcenniejsze niewątpliwie podstawy ze wszystkiemi
dowodzeniami. Tymi też mogę was przekonać i nie potrzebuję zajmować was
rzeczami prawdopodobnymi, gdyż początki mechaniki są wam znane, o ile
się na nich trzeba będzie opierać. Przede wszystkiem rozpatrzmy co się
dzieje, gdy łamiemy kawałek drzewa, lub jakieś inne ciało, którego
cząstki mocno są ze sobą związane, gdyż tu znajdziemy pierwszą i
najprostszą zasadę, na której wszystko polega. Dla lepszego
zrozumienia bierzemy pod uwagę (rys. 1) walec lub
graniastosłup AB, z drzewa lub innego materiału, mocnego i spójnego,
umocowany swym górnym końcem w A, wiszący pionowo i obciążony u spodu
ciężarem C. Jakakolwiek jest jego wytrzymałość i spójność
międzycząsteczkowa, byleby tylko nie była nieskończona, to można ją
zawsze pokonać ciężarem C, jeżeli przypuścimy, że ten ciężar można
dowolnie powiększać, tak że walec zostanie rozerwany, jak powróz. A tak
jak w powrozie przypuszczamy, że wytrzymałość pochodzi z włókien, z
których lina się składa, to również drzewo składa się z włókien,
mianowicie z długich słojów, które czynią drzewo wytrzymałym na
rozerwanie w większym stopniu, niż włókna powrozu tej samej grubości. W
walcu kamiennym lub metalowym wytrzymałość zależy od innego środka,
wiążącego cząstki jedne z drugimi, ale i taki walec się rozrywa przy
mocnem rozciąganiu.
SALVIATI: Jestem na usługi Waszmościów, jeżeli tylko zdołam sobie
przypomnieć wszystko, czego się nauczyłem od naszego Akademika, który
wiele rozmyślał o tych rzeczach i zawsze na podstawie swojej metody
geometrycznej, tak że nie bez racji możnaby to nazwać nową
umiejętnością. Więc, jakkolwiek niektóre zasady przez innych, a
najpierw przez Arystotelesa były wywiedzione, to jednak tu są
najpiękniejsze i najcenniejsze niewątpliwie podstawy ze wszystkiemi
dowodzeniami. Tymi też mogę was przekonać i nie potrzebuję zajmować was
rzeczami prawdopodobnymi, gdyż początki mechaniki są wam znane, o ile
się na nich trzeba będzie opierać. Przede wszystkiem rozpatrzmy co się
dzieje, gdy łamiemy kawałek drzewa, lub jakieś inne ciało, którego
cząstki mocno są ze sobą związane, gdyż tu znajdziemy pierwszą i
najprostszą zasadę, na której wszystko polega. Dla lepszego
zrozumienia bierzemy pod uwagę (rys. 1) walec lub
graniastosłup AB, z drzewa lub innego materiału, mocnego i spójnego,
umocowany swym górnym końcem w A, wiszący pionowo i obciążony u spodu
ciężarem C. Jakakolwiek jest jego wytrzymałość i spójność
międzycząsteczkowa, byleby tylko nie była nieskończona, to można ją
zawsze pokonać ciężarem C, jeżeli przypuścimy, że ten ciężar można
dowolnie powiększać, tak że walec zostanie rozerwany, jak powróz. A tak
jak w powrozie przypuszczamy, że wytrzymałość pochodzi z włókien, z
których lina się składa, to również drzewo składa się z włókien,
mianowicie z długich słojów, które czynią drzewo wytrzymałym na
rozerwanie w większym stopniu, niż włókna powrozu tej samej grubości. W
walcu kamiennym lub metalowym wytrzymałość zależy od innego środka,
wiążącego cząstki jedne z drugimi, ale i taki walec się rozrywa przy
mocnem rozciąganiu.
SIMPLICIO: Skoro tak się mają rzeczy, jak
mówicie, to rozumiem, że słoje drzewa, równie długie jak samo drzewo,
nadają mu wytrzymałość na rozerwanie; ale dlaczego lina, której
pojedyncze włókna mogą mieć najwyżej 2 do 3 łokci długości, może mieć
100 łokci długości i wytrzymywać rozciąganie? Pragnąłbym także poznać
wasz pogląd na spoistość między cząstkami metalu lub kamienia lub
innego materiału, nie złożonego z włókien, który jednak, jeżeli się nie
mylę, może być jeszcze wytrzymalszy.
SALVIATI: Nowymi rozważaniami, więcej odległymi od naszego
przedmiotu, będziemy mogli się zająć, skoro rozwiążemy całkowicie
napotkane dotąd trudności.
SAGREDO: Jeżeli jednak
zboczenie z drogi prowadzić nas może do poznania nowych prawd, co nam
przeszkadza zboczyć, skoro nie jesteśmy zmuszeni postępować według
ściśle ograniczonej metody i możemy nasze rozmowy prowadzić według
upodobania - i dlaczego nie mamy się zatrzymywać nad spotkanymi
kwestiami, które mogą się już drugi raz nie przedstawić? Następnie: kto
wie, czy nie trafimy właśnie na takie rzeczy, które są bardziej
interesujące i piękniejsze od wniosków, do jakich doszliśmy na
początku. Toteż proszę Waszmość o zastosowanie się do życzenia p.
Simplicia a zarazem i mojego, gdyż pragnąłbym zaraz wiedzieć, jakie
jest wiązadło, łączące tak mocno cząstki ciał stałych, że wydają się
ostatecznie nierozerwalnemi: wiadomość ta jest potrzebna dla
objaśnienia spoistości między cząstkami włókien, z których składają się
ciała.
SALVIATI: Rozważajmy więc dalej, skoro tak chcecie. Pierwsza
trudność była: jak mogą włókna liny o długości stu łokci (gdy same nie
mają więcej niż 2 do 3 łokci), przylegać tak mocno do siebie, że tylko
wielką siłą mogą być rozerwane. Ale powiedz mi, Waszmość p. Simplicio,
czy nie potrafisz trzymać tak mocno palcami pojedynczego włókna
konopnego za jeden koniec, że, ciągnąc je za drugi koniec, prędzej je
rozerwę, aniżeli je wam z ręki wyciągnę. Jeżeli więc włókno konopne
ściskane jest tak mocno przez swe otoczenie, nie tylko na końcach, ale
na całej swej długości, czyż to nie jest przyczyną, że oderwanie włókna
od tego otoczenia staje się trudniejsze od przerwania samego włókna.
Skręcanie liny tak przyciska włókna jedne do drugich, że przy
jak najmocniejszem wyciąganiu liny raczej się łamią, aniżeli oddzielają
od siebie: jak przekonać się można, otrzymując w miejscu rozerwania
liny krótkie końce włókien nie mające ani łokcia długości, jakby to
miało miejsce, gdyby lina rozrywała się nie wskutek rozdarcia włókien,
ale ich oddzielenia się od włókien otaczających.
SAGREDO: Na potwierdzenie tego mogę dodać, że nieraz lina się
przerywa nie wskutek rozciągania wzdłuż, ale nadzwyczaj mocnego
skręcania; dowodzi to, że włókna są w linie wzajemnie tak ściskane, że
naciskające nie pozwalają naciskanym na jak najmniejsze wyślizgnięcie,
konieczne do wydłużenia skrętów, aby mogły linę wkoło otoczyć; gdyż przy
skręcaniu lina się skraca i wskutek tego nieco grubieje.
(...)
SALVIATI: (...) spójność między częściami tych ciał zależy od różnych
okoliczności, które zdaniem mojem sprowadzają się do dwóch, jedną jest
tak sławiony wstręt natury do tworzenia próżni, a drugą stanowi (gdy
pierwsza nie wystarcza) środek wiążący, lepki i kleisty, który cząstki
ciała mocno ze sobą wiąże. Najpierw zajmijmy się próżnią i wykażmy
jasnymi doświadczeniami, jaka i jak wielka jest jej własność. Weźcie,
proszę, dwie tafle z marmuru, metalu lub szkła, ściśle płaskie, gładkie
i mogące się przesuwać jedna po drugiej. Jeżeli jedną na drugą położymy,
to łatwo je można przesuwać (oczywiście gdy ich żaden klej nie wiąże),
przy odejmowaniu wszakże jednej od drugiej ujawnia się taki opór, że
podnoszona tafla górna zatrzymuje przy sobie dolną, choćby wielką i
ciężką. Dowodzi to widocznie wstrętu natury do tworzenia próżni, choćby
na krótki czas, która by powstała, zanim ją wypełni powietrze otaczające.
Widzimy także, że, gdy tafle nie są gładko wypolerowane, tak że
zetknięcie ich nie jest zupełne, to przy powolnym ich rozłączaniu nie
można zauważyć żadnego oporu, jak tylko wywołany ciężarem zdejmowanej
tafli, ale przy szybkim zdejmowaniu wierzchniej tafli, zrazu przylega
do niej jeszcze tafla dolna, by opaść po chwili; trzyma się bowiem tylko
tyle czasu, ile potrzeba na wyjście małej ilości powietrza znajdującego
się między taflami, niezupełnie ściśle przylegającemi i umożliwienie
wejścia nowej ilości powietrza. Opór ten, ujawniający się tak dotykalnie
między taflami, ma miejsce także między cząstkami ciała stałego i
przynajmniej w części stanowi przyczynę ich spójności.
SAGREDO: Proszę, zatrzymajcie się i pozwólcie mi zauważyć jedną
okoliczność, która właśnie przychodzi mi na myśl: mianowicie, skoro
dolna tafla podniesiona zostaje przez górną, zwłaszcza przy bardzo
szybkim zdejmowaniu ostatniej, to wydaje mi się jasne, że wbrew
mniemaniu filozofów, a zwłaszcza Arystotelesa, ruch w próżni nie mógłby
natychmiast nastąpić; bo gdyby tak było, to musiałyby obie tafle bez
żadnego oporu się rozłączyć, gdyż ten sam czas winien wystarczać, aby
się od siebie oderwały i aby próżnia, między nimi wytworzona,
wypełniona została przez powietrze otaczające. Zatem z tego, że dolna
tafla nie oddzieliła się, wnioskować należy: że w próżni ruch nie może
powstać w jednej chwili i że między taflami tworzy się próżnia, krótki
czas przynajmniej, ten właśnie, który upływa podczas ruchu pomiędzy
wejściem a wyjściem otaczającego powietrza - i dalej, że gdy żadna
próżnia nie powstaje, to nie może być mowy o ruchu powietrza
otaczającego. Należy przeto powiedzieć, że właśnie przez gwałtowność
ruchu a przeciw prawu natury powstaje czasem próżnia (jakkolwiek sądzę,
że nic nie może się dziać przeciw naturze, chyba to, co jest niemożliwe,
a to też nigdy się nie dzieje). Tu wszakże spotykam inną trudność,
mianowicie tę, że jakkolwiek badanie przekonuje mnie o prawdziwości
wniosku, umysł wszakże nie jest całkowicie zadowolony z przyczyny, której
należy przypisać ten skutek. Bo rozdzielenie obu tafli następuje przed
powstaniem próżni, która jako skutek wytwarza się po nim; a ponieważ,
jak mi się zdaje, przyczyna, jeżeli nie następuje równocześnie z
działaniem, winna je poprzedzać i pozytywny skutek winien odpowiadać
pozytywnej przyczynie, to nie pojmuję, jak przyczyną przylegania obu
tafli i oporu, jaki one stawiają rozdzielaniu, więc działań, które już
są aktualne, może być próżnia, której jeszcze nie ma i która dopiero ma
powstać. Rzeczy zaś, których nie ma, nie mogą wywierać żadnego działania,
zgodnie z niezachwianem orzeczeniem Filozofa.
SIMPLICIO: Jeżeli przyjmujecie tę zasadę Arystotelesa, to spodziewam
się, że nie będziecie przeczyli innej pięknej jego zasadzie, a
mianowicie następującej: natura nie bierze się do tworzenia tego, co
się opiera swemu powstaniu: i w tej zasadzie tkwi rozwiązanie naszej
zagadki, gdyż próżnia sama przez się opiera się swemu powstaniu, a
jednocześnie natura wzbrania się uczynić to, co mogłoby wytworzyć
próżnię; to właśnie ma miejsce przy rozłączaniu tafli.
SAGREDO: Kwestia, jaką podniosłem, rozwiązana zostaje przez uwagę p.
Simplicia, a wracając do zawiązku naszej rozmowy, wydaje mi się, że
opór stawiany wytworzeniu próżni stanowi wystarczającą podstawę
spoistości między cząstkami ciała stałego, czy to będzie kamień, metal,
albo inny materiał jeszcze mocniejszy. Bo jeżeli każde działanie ma
zawsze swoją przyczynę, jak to zawsze myślałem, albo też skoro można
wykryć kilka przyczyn, to te wszystkie sprowadzić się dają do jednej:
więc dlaczegoż by tu próżnia, która na pewno się wytwarza, nie miałaby
stanowić podstawy wystarczającej wszystkich objawów wytrzymałości.
SALVIATI: Nie będę się obecnie zajmował kwestią, czy sama próżnia,
bez innej pomocy, wystarcza do spojenia cząstek ciała stałego; ale
twierdzić mogę, że ta przyczyna, która wprawdzie istnieje i wystarcza do
objaśnienia przylegania tafli, nie tłumaczy dostatecznie wytrzymałości
walca marmurowego albo metalowego, który, silnie rozciągany, w końcu
ustępuje i pęka. A jeżeli znajdę sposób rozróżnienia rozpoznanego już
oporu, pochodzącego z próżni, od wszelkich innych, jakiekolwiek one są,
razem z nim tworzących spójność ciał i jeżeli będę wam mógł wykazać, że
żadna główna przyczyna sama jedna nie wystarcza do wytworzenia tego
skutku, to przyznacie, że trzeba tu wprowadzić inną. Pomóżcie mu, p.
Simplicio, bo p. Sagredo jest w niepewności co do odpowiedzi.
SIMPLICIO: Pewno wstrzymanie się p. Sagredo ma inną przyczynę, bo
nie można mieć wątpliwości co do tak jasnego i koniecznego wniosku.
SAGREDO: Odgadłeś, panie Simplicio. Myślałem o tym, czy, jeżeli
milion złota rocznie, jaki przychodzi z Hiszpanji na opłacenie
żołnierzy, nie wystarcza, to potrzeba zrobić inny zapas pieniędzy dla
utrzymania armii. Ale mów pan dalej, p. Salviati, przyjmując, że
zgadzam się na wniosek, do jakiego dochodzisz i pokaż nam sposób
oddzielenia działania próżni od innych działań, a mierząc próżnię,
pokaż, jak ona się zmniejsza przez działanie, o którym mowa.
 SALVIATI: Bądźcie więc dobrej myśli. Zakomunikować Wam pragnę, w
jaki sposób potęga próżni może być oddzielona od innych sił i jak ją
można zmierzyć. Dla jej wyosobnienia weźmy pod uwagę ciało, które sile
dążącej do rozerwania jego cząstek nie stawia innego oporu jak tylko
próżnię, a nasz akademik dowiódł w swoim traktacie, że takim ciałem
właśnie jest woda. Jeżeli więc tak umieścimy walec z wody, aby można
było wykazać jego wytrzymałość na rozerwanie, to ta wytrzymałość nie
będzie miała innej przyczyny, jak tylko opór stawiany przez próżnię.
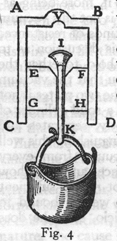
Dla wykonania takiego doświadczenia obmyśliłem przyrząd, który
rysunkiem łatwiej niż słowami mogę wam przedstawić. Niech będzie CABD
(rys. 4) przekrój cylindra metalowego lub szklanego, którego
wnętrze byłoby jak najregularniej obtoczone i do tego wnętrza przylegał
ściśle wałek pełny z drzewa EFGH, mogący się posuwać w cylindrze i mający w środku otwór, przez który przechodzi zatyczka żelazna,
zakrzywiona u spodu K, a mająca na wierzchu zgrubienie ostro-kręgowe l,
zamykające ściśle lejkowaty wierzch otworu w wałku pełnym, gdy zatyczka
pociągnięta zostanie do dołu. W cylindrze próżnym AD jest więc tłok
drewniany EH nie dochodzący na 2 do 3 palców do wierzchu cylindra. Cylinder, postawiony spodem do
góry, wypełniony zostaje wodą, która wchodzi przez otwór wokół zatyczki
l, gdy ta jest trochę wepchnięta do środka, a przez tenże otwór wychodzi
powietrze. Po wyjściu wszystkiego powietrza, przez pociągnięcie
zatyczki zamykamy szczelnie otwór i wtedy odwracamy cylinder i
zawieszamy na haczyku naczynie, do którego możemy sypać tyle piasku lub
innego ciężaru aż się w końcu powierzchnia tłoka EF oderwie od wody.
Ponieważ trzymały się one tylko siłą oporu próżni, przeto po zważeniu
tłoka, drutu i naczynia otrzymamy wielkość tego oporu. Jeżeli na walcu
marmurowym lub szklanym zawiesimy tyle ciężaru, ile waży takiż walec
wody i dodamy jeszcze tyle, że razem z ciężarem marmuru mieć będziemy
ciężar wszystkich wymienionych obciążeń, to, gdyby wtedy nastąpiło
rozerwanie, moglibyśmy przyjąć za rzecz niewątpliwą, że próżnia stanowi
jedyną przyczynę wytrzymałości marmuru. Skoro wszakże pod tym ciężarem
ani pod cztery razy większym, nie można rozerwać marmuru, to należy
wnioskować że opór próżni wynosi tylko piątą część ogólnej
wytrzymałości, a jej reszta jest cztery razy większa od oporu próżni.
SALVIATI: Bądźcie więc dobrej myśli. Zakomunikować Wam pragnę, w
jaki sposób potęga próżni może być oddzielona od innych sił i jak ją
można zmierzyć. Dla jej wyosobnienia weźmy pod uwagę ciało, które sile
dążącej do rozerwania jego cząstek nie stawia innego oporu jak tylko
próżnię, a nasz akademik dowiódł w swoim traktacie, że takim ciałem
właśnie jest woda. Jeżeli więc tak umieścimy walec z wody, aby można
było wykazać jego wytrzymałość na rozerwanie, to ta wytrzymałość nie
będzie miała innej przyczyny, jak tylko opór stawiany przez próżnię.
Dla wykonania takiego doświadczenia obmyśliłem przyrząd, który
rysunkiem łatwiej niż słowami mogę wam przedstawić. Niech będzie CABD
(rys. 4) przekrój cylindra metalowego lub szklanego, którego
wnętrze byłoby jak najregularniej obtoczone i do tego wnętrza przylegał
ściśle wałek pełny z drzewa EFGH, mogący się posuwać w cylindrze i mający w środku otwór, przez który przechodzi zatyczka żelazna,
zakrzywiona u spodu K, a mająca na wierzchu zgrubienie ostro-kręgowe l,
zamykające ściśle lejkowaty wierzch otworu w wałku pełnym, gdy zatyczka
pociągnięta zostanie do dołu. W cylindrze próżnym AD jest więc tłok
drewniany EH nie dochodzący na 2 do 3 palców do wierzchu cylindra. Cylinder, postawiony spodem do
góry, wypełniony zostaje wodą, która wchodzi przez otwór wokół zatyczki
l, gdy ta jest trochę wepchnięta do środka, a przez tenże otwór wychodzi
powietrze. Po wyjściu wszystkiego powietrza, przez pociągnięcie
zatyczki zamykamy szczelnie otwór i wtedy odwracamy cylinder i
zawieszamy na haczyku naczynie, do którego możemy sypać tyle piasku lub
innego ciężaru aż się w końcu powierzchnia tłoka EF oderwie od wody.
Ponieważ trzymały się one tylko siłą oporu próżni, przeto po zważeniu
tłoka, drutu i naczynia otrzymamy wielkość tego oporu. Jeżeli na walcu
marmurowym lub szklanym zawiesimy tyle ciężaru, ile waży takiż walec
wody i dodamy jeszcze tyle, że razem z ciężarem marmuru mieć będziemy
ciężar wszystkich wymienionych obciążeń, to, gdyby wtedy nastąpiło
rozerwanie, moglibyśmy przyjąć za rzecz niewątpliwą, że próżnia stanowi
jedyną przyczynę wytrzymałości marmuru. Skoro wszakże pod tym ciężarem
ani pod cztery razy większym, nie można rozerwać marmuru, to należy
wnioskować że opór próżni wynosi tylko piątą część ogólnej
wytrzymałości, a jej reszta jest cztery razy większa od oporu próżni.
SIMPLICIO: Nie można przeczyć, że wynalazek jest dowcipny, zauważyłem
wszakże wiele trudności, które mi przedstawiają rzecz całą jako
wątpliwą; któż bowiem zapewni, że powietrze nie przechodzi przez szkło
lub tłok, jakkolwiek są one uszczelnione pakułami lub inną materją
ściślejszą; a następnie, choćby koniec I zatyczki zamykał ściśle
rozszerzenie ostrokręgowe otworu, wypadłoby je może wysmarowaó
woskiem lub terpentyną. Dlaczego by zresztą cząstki wody nie miały się
rozchodzić i rozrzedzać; dlaczego by nie wchodziło powietrze albo
inne pary lub substancje, subtelniejsze od porów drzewa a nawet szkła?
SALVIATI: Nader zręcznie przedstawia nam p. Simplicio trudności,
po części dając nam sposoby ich usunięcia, zwłaszcza co się tyczy
przechodzenia powietrza przez drzewo i szkło. Zaznaczę wszakże, że
możemy jednocześnie uważać, jako nabyte, nowe wiadomości, jeżeli
powyższe trudności istotnie mają miejsce. Bo gdyby woda, choćby przy
użyciu siły, była z natury swej rozciągliwa, jak się to dzieje z
powietrzem, to ujrzelibyśmy, że tłok się opuszcza; a gdybyśmy w górnej
części cylindra szklanego urządzili w środku zagłębienie, jak w V, to
zbierać się tam będzie wszelka materia subtelna, przechodząca przez
pory drzewa lub szkła, albo też powietrze przechodzące przez tłok. Gdy
wszakże nie widzimy tego, to musimy uważać doświadczenie za wykonane
z całą ścisłością i uznać, że woda nie jest rozciągliwa, a szkło jest
nieprzenikliwe nawet dla najsubtelniejszych substancji.
SAGREDO: Ja zaś cieszę się, że z tej rozprawy wyłoniła
się przyczyna zjawiska, które mi się przez długi czas wydawało cudowne i niepojęte.
Obserwowałem studnię, na której dla czerpania wody ustawił ktoś pompę,
w nadziei otrzymania wody z mniejszym trudem, a w większej ilości, niż
przy użyciu zwykłych wiader. Pompa ta miała tłok i wentyl tak wysoko
umieszczone, że podawała wodę przez ssanie a nie przez tłoczenie, jak
pompy mające takie urządzenie u spodu. Pompa dostarczała wody obficie,
gdy poziom w studni dochodził do pewnej wysokości, skoro wszakże poziom
się obniżał, pompa przestawała działać. Sądziłem zrazu, zaobserwowawszy
taki przypadek, że pompa zepsuta i uprzedziłem majstra dla naprawy, ten
wszakże zapewnił mnie, że nie ma żadnego braku a tylko woda zbyt nisko
stojąca w studni nie może być podawana na taką wysokość; nadmienił, że
ani pompy ani inne maszyny, podnoszące wodę przez ssanie, nie mogą jej
podnosić ani na włos wyżej niż 18 łokci i czy pompa będzie
szeroka czy wąska, to taka będzie zawsze najwyższa granica podnoszenia.
A ja dotychczas nie wiedziałem, że podobnie jak sznur, drzewo lub szkło,
łatwiej jeszcze słup wody się rozrywa, gdy jest rozciągany działaniem
własnego ciężaru. Cóż bowiem innego rozciągamy w pompie jeżeli nie walec
pełen wody u góry umocowany i wciąż wydłużany, aż dojdziemy
do granicy, przy której dalsze wydłużenie rozrywa walec wodny jak sznur.
SALVIATI: Rzecz się ma tu w ten sam sposób i ponieważ właśnie 18
łokci stanowi tę granicę, przy której każda ilość wody, w rurze
szerokiej czy wąskiej lub jak najwęższej, tak wąskiej jak słomka, może
być podnoszona, to będziemy zawsze, bez względu na to, czy przekrój
będzie większy lub mniejszy, mieli wartość oporu jaki stawia próżnia w
słupie utworzonym z jakiejkolwiek materii, gdy tylko grubość słupa jest
taka, jak wewnętrzne światło rury. l jakkolwiek wiele już mówiliśmy o
tym, to jeszcze zaznaczę, jak łatwo znaleźć można, do jakiej długości ma
dochodzić słup, czy to drut czy sztaba dowolnej grubości, aby się
rozrywała pod działaniem własnego ciężaru. Weźmy np. drut miedziany,
jakiejkolwiek długości, przytwierdźmy jego górny koniec gdziekolwiek i
obciążajmy coraz więcej koniec dolny, aż dopókąd drut się nie
przerwie. Jeżeli się przerwie przy pięćdziesięciu funtach obciążenia,
to jasne jest, że pięćdziesiąt funtów miedzi, dodane do własnego
ciężaru drutu, wynoszącego zaledwie 1/8 uncji,
i wyciągnięte w takiż sam drut, dadzą długość maximalną drutu
miedzianego, mogącego wytrzymać własny ciężar. Zmierzmy więc, jaka jest
długość tego drutu, który się przerywa. Jeżeli ma jeden łokieć długości,
to ponieważ waży1/8 uncji i unosi nadto 50
funtów miedzi, które stanowili 4800 ósmych części uncji, to wynika stąd,
że drut miedziany, jakiejkolwiek grubości może utrzymać swój ciężar
własny, o ile jego długość nie przenosi 4800 łokci i dalej że pręt
miedziany, aby mógł utrzymać swój ciężar do tej długości, winien mieć
wytrzymałość tyle razy większą od oporu próżni, ile razy jego ciężar
jest większy od ciężaru pręta wodnego tej samej grubości, a długości 18
łokci. A ponieważ miedź jest 19 razy cięższa od wody, przeto część
wytrzymałości pochodząca od oporu próżni wynosi tyle, ile ciężar 2 łokci
pręta tejże grubości. Tak samo obliczyć można długość każdego sznura,
liny lub innego materiału, mogącą utrzymać własny ciężar oraz część
wytrzymałości, jaka w tym przypada na próżnię.
SAGREDO: Pozostaje jeszcze abyście wyjaśnili, z czego się
składa pozostała część wytrzymałości, albo, co to jest za środek wiążący
czy zlepiający, który utrzymuje w zetknięciu cząstki ciała stałego,
oprócz tego, który polega na próżni. Nie mogę bowiem wyobrazić sobie
takiego kleju, który by w wielkim ogniu nie spalił się lub nie zniszczył
w ciągu 2, 3 i 4 miesięcy a nawet 10 lub 100. Gdyż srebro, złoto lub
szkło, pozostawszy tak długo roztopione, po oziębieniu wracają do stanu
stałego i do poprzedniej spoistości cząstek. Nadto tez samą trudność,
którą mam w spoistości cząstek szkła, będę znów miał przy rozważaniu
spoistości cząstek kleju, lub innego środka wiążącego.
SALVIATI: Powiedziałem przed chwilą: bądźcie dobrej myśli i jeszcze o
to się troszczę, i jeszcze odczuwam ręką, że to niewątpliwie opór
próżni nie pozwala rozdzielić dwóch tafli, jak tylko z wielkim
wysiłkiem i że dwie duże połowy słupa z marmuru lub brązu trzymają się
razem jeszcze mocniej. Nie sadzę też, aby to mogło polegać na spójności
najmniejszych cząstek, aż do najdrobniejszych tej materii. Każde zaś
działanie musi mieć pewną istotną i główną przyczynę a ja, nie
znajdując innego środka wiążącego, dlaczegóż bym nie miał się starać o
zbadanie, czy może jednak sama próżnia będzie tu wystarczająca dla
objaśnienia?
SIMPLICIO: Ponieważ dowiedliście, że opór wielkiej próżni, przy
rozrywaniu wielkich części ciała stałego, jest bardzo mały w porównaniu
ze spoistością małych cząsteczek, dlaczegóż nie chcecie przyjąć za
niemniej pewne, że ten opór jest czemś rożnym od próżni?
SALVIATI: Na to odpowie p. Sagredo, że jednak wszystkich
pojedynczych żołnierzy płaci się pieniędzmi, które zbiera się przez
ogólne podatki w soldach i denarach, podczas gdy miliona złota potrzeba
na opłacenie całej armii. I kto wie, czy inne maleńkie próżnie nie
działają właśnie przy najmniejszych cząsteczkach, tak że wszędzie taż
sama moneta trzyma wszystkie części złączone. Powiadam wam to, co mi w
tej chwili przychodzi na myśl i nie podaję tego jako prawdę absolutną,
lecz jako pomysł jeszcze nie przetrawiony, pozostawiając go głębszej
rozwadze. Weźcie z niego, co się wam podoba, a resztę osądźcie jak
chcecie. Gdy widziałem wielokrotnie, jak ogień przebywa wężykiem między
najmniejszymi cząstkami metalu, które mocno się ze sobą trzymały, a w
końcu się rozpadały i jak potem, wyjęte z ognia wracały do pierwotnej
spoistości, przy czym ilość złota zupełnie się nie zmniejszyła, a bardzo
mało przy innych metalach i to po długim czasie pozostawania roztopionymi;
myślałem wtedy, że się to dzieje w ten sposób, że najmniejsze cząstki
ognia wchodzą w ciasne pory metalu (do których, z powodu ich
szczupłości, ani powietrze ani żaden inny płyn wejść nie może); tym
sposobem mogłyby być wypełnione najmniejsze próżnie między cząstkami,
co by zwolniło najmniejsze cząstki siły, z którą się te próżnie wzajemnie
przyciągają i sprzeciwiają rozsuwaniu; gdy przez to cząstki mogą się
swobodnie poruszać, masa staje się płynną i pozostaje taką dopóty,
dopóki ogień ją przenika; gdy zaś ten ustaje, pozostają pierwsze
próżnie i wraca przyciąganie wiążące ze sobą cząstki. Na zarzut zaś p.
Simplicia można odpowiedzieć, że jakkolwiek te próżnie są bardzo małe, a
więc opór każdej z nich z łatwością może być przezwyciężony, to jednak
niezliczona ich liczba mnoży niezliczenie (że się tak wyrażę)
wytrzymałość; jaka zaś i jak wielka siła powstać może z olbrzymiej
liczby bardzo słabych, razem złączonych momentów, o tym sądzić można
przez analogię, wiedząc jak ciężar miljona funtów, wiszący na bardzo
grubej linie konopnej, obniża się, ale w końcu zostaje przezwyciężony,
gdy w konopie wchodzą niezliczone cząstki wody, które albo wiatr
południowy przynosi, albo też, które jak delikatne chmurki unoszone są
przez powietrze. Przeciskają się one od jednego włókna do drugiego w
najściślejszej linie, i nawet zawieszony olbrzymi ciężar nie może im
wzbronić dostępu: tak się przeciskają przez cienkie szpary i zgrubiają
linę, skręcając ją, przez co podniesiony być może największy ciężar.
SAGREDO: Nie ma zatem wątpliwości, że skoro pewien opór nie
jest nieskończenie wielki, to może być zawsze pokonany przez wielką
liczbę bardzo małych sił; tak że nawet pewna liczba mrówek może
wciągnąć na ląd okręt naładowany zbożem; możemy bowiem obserwować
codziennie, jak jedna mrówka niesie ziarno; na okręcie zaś nie ma
nieskończonej liczby ziarn, a tylko znajduje się ich tam pewna liczba,
którą pomyśleć nawet można cztery lub sześć razy większą; może więc pewna liczba mrówek wciągnąć okręt ze zbożem na ląd. To
prawda, że trzeba, aby ta liczba była bardzo wielka, ale też sądzę, że i
pory w metalach są również bardzo liczne.\
SALVIATI: Uważaliście jednak za niemożliwe, żeby ich liczba
była nieskończoną.
SAGREDO: Nie, skoro tylko metal jest masą skończoną,
inaczej ...
SALVIATI: Inaczej co? Ale skoro już doszliśmy do
paradoksów, zobaczmy, czy nie moźna by dowieść jakim sposobem, że na
pewnej skończonej długości ciągłej może się znajdować nieskończenie
wiele próżni. Zobaczymy jednocześnie, czy się nie znajdzie, jeśli już
nie co innego, to przynajmniej przybliżone rozwiązanie najwięcej
zadziwiającego zadania,
 zaliczonego przez Arystotelesa do godnych
podziwu, a dodam, należących do mechaniki; rozwiązanie to mogłoby być
nie mniej zadowalające, jak jego własne, a jednocześnie odmienne od
rozwiązania uczonego monsignora di Guevara. Najpierw wszakże trzeba
podać twierdzenie, nie tknięte przez innych, od którego zależne jest
rozwiązanie zadania i z którego, jeśli się nie mylę, dadzą się wyciągnąć
inne wiadomości nowe i godne podziwu. Dla ściślejszego zrozumienia
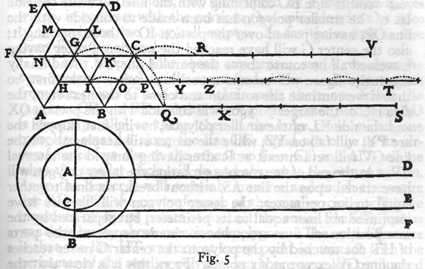
narysujmy figurę. (rys. 5) Niech będzie równoboczny i
równokątny wielobok, o jakiejkolwiek liczbie boków, ze środkiem w G.
Mamy więc sześciokąt ABCDEP, w który wpiszemy drugi współśrodkowy
HIKLMN. Przedłużmy bok AB większego wieloboku do S i odpowiednio bok HI
mniejszego w tym samym kierunku, tak że HT będzie równoległe do AS,
wreszcie przez środek G poprowadźmy równoległą GV. Gdy to jest zrobione,
toczmy wielobok większy, razem z małym, po linii AS. Jasne jest, że w
początku toczenia, B stoi w miejscu, A się podnosi, a C obniża
zakreślając łuk CQ, dopóki się bok BC nie położy na linii AS, jako BQ = BC. Przy tym
obrocie wszakże, wierzchołek l małego wieloboku wzniesie się ponad
linię IT, bo IB jest nachylone względem AS, a I nie wcześniej dojdzie do
równoległej IT, aż gdy C dojdzie do Q: wtedy I padnie na O, po opisaniu
łuku I0, ponad HT a IK zajmie położenie OP. Ale środek G będzie
tymczasem w ruchu ponad linią GV i nie wcześniej do niej wróci, jak po
przebieżeniu łuku GC. Po zrobieniu tego pierwszego kroku, będzie większy
wielobok leżał bokiem BC na BQ, bok małego wieloboku IK na OS, podczas
gdy cała droga I0 zostanie przeskoczona bez dotknięcia, a środek G
przejdzie do C, przebywając drogę poza równoległą GV. W końcu cała
figura zajmie położenie podobne do pierwszego, tak że przy dalszym
obrocie i drugim kroku, bok większego wieloboku DC położy się na QX,
bok małego wieloboku KL, po przekroczeniu PX na YZ, a środek G,
poruszający się wciąż ponad GV, zejdzie tam dopiero w R, po wielkim
skoku CR. W rezultacie, większy wielobok, tocząc się po AS, odetnie
sześć linii równych jego obwodowi, bez żadnych przerw; wielobok
mniejszy pokryje również sześć jednakich odcinków, równych jego
obwodowi, ale poprzegradzanych pięcioma łukami, których cięciwy nie będą
dotknięte, stanowiąc części linii HT; wreszcie środek G w sześciu
punktach tylko schodzić się będzie z równoległą GV. Pojmujecie więc. że
przestrzeń HT, przebyta przez mały wielobok, jest prawie równą AS,
przebytej przez wielobok większy, od której jest mniejsza tylko o jedną
cięciwę małego łuku, uważając linię HT razem z pięcioma łukami.
Pragnąłbym teraz, aby to, co wam przedstawiłem na przykładzie tych
sześcioboków, okazało się wam również jasne przy innych wielobokach, z
dowolną liczbą boków, a tylko do siebie podobnych, współśrodkowych i
razem ze sobą związanych, tak że przy toczeniu się większych rozważać
można toczenie się mniejszych i że drogi przebyte są prawie równe, o
ile się dolicza przestrzenie pod łukami, nie dotknięte bokami
mniejszego wieloboku. Niech więc będzie większy wielobok o 1000 boków,
które odcinamy na przebytej przezeń drodze. Równocześnie mały wielobok
przebywa prawie tę samą drogę, dotknąwszy się 1000 małych odcinków,
przegrodzonych 1000 próżni, gdyż tak je możemy nazwać w przeciwieństwie
do 1000 odcinków dotkniętych. To, co powiedziałem, nie przedstawia żadnej
trudności ani wątpliwości. Ale powiedzcie mi, jeżeli około jakiego
środka np. A, zakreślimy dwa koła współśrodkowe, związane razem i jeżeli
z końców ich średnic C i B poprowadzimy dwie styczne CE, BF, a przez
środek A równoległą AD i jeżeli toczyć będziemy koło większe po BF (i
uczynimy BF równe obwodowi koła równie jak i linie CE i AD), to po
jednym obrocie cóż się stanie z małym kołem i ze środkiem? Ten ostatni
przebiegnie niewątpliwie całą długość AD, a obwód małego koła dotknie
się swymi punktami całej linii CE, w ten sam sposób jak to było
poprzednio z wielobokiem; z tą jedyną różnicą, że tam linia HT nie we wszystkich punktach była
dotykana przez mały wielobok, bo wiele małych odcinków było
przeskoczonych, tu zaś przy kole nie może jego obwód opuszczać ani na
chwilę linii CE i każdy jego punkt musi się na niej znajdować. W jaki
więc sposób może mniejsze koło, bez przeskakiwania, przebiec drogę tak
znacznie dłuższą od swego okręgu?
zaliczonego przez Arystotelesa do godnych
podziwu, a dodam, należących do mechaniki; rozwiązanie to mogłoby być
nie mniej zadowalające, jak jego własne, a jednocześnie odmienne od
rozwiązania uczonego monsignora di Guevara. Najpierw wszakże trzeba
podać twierdzenie, nie tknięte przez innych, od którego zależne jest
rozwiązanie zadania i z którego, jeśli się nie mylę, dadzą się wyciągnąć
inne wiadomości nowe i godne podziwu. Dla ściślejszego zrozumienia
narysujmy figurę. (rys. 5) Niech będzie równoboczny i
równokątny wielobok, o jakiejkolwiek liczbie boków, ze środkiem w G.
Mamy więc sześciokąt ABCDEP, w który wpiszemy drugi współśrodkowy
HIKLMN. Przedłużmy bok AB większego wieloboku do S i odpowiednio bok HI
mniejszego w tym samym kierunku, tak że HT będzie równoległe do AS,
wreszcie przez środek G poprowadźmy równoległą GV. Gdy to jest zrobione,
toczmy wielobok większy, razem z małym, po linii AS. Jasne jest, że w
początku toczenia, B stoi w miejscu, A się podnosi, a C obniża
zakreślając łuk CQ, dopóki się bok BC nie położy na linii AS, jako BQ = BC. Przy tym
obrocie wszakże, wierzchołek l małego wieloboku wzniesie się ponad
linię IT, bo IB jest nachylone względem AS, a I nie wcześniej dojdzie do
równoległej IT, aż gdy C dojdzie do Q: wtedy I padnie na O, po opisaniu
łuku I0, ponad HT a IK zajmie położenie OP. Ale środek G będzie
tymczasem w ruchu ponad linią GV i nie wcześniej do niej wróci, jak po
przebieżeniu łuku GC. Po zrobieniu tego pierwszego kroku, będzie większy
wielobok leżał bokiem BC na BQ, bok małego wieloboku IK na OS, podczas
gdy cała droga I0 zostanie przeskoczona bez dotknięcia, a środek G
przejdzie do C, przebywając drogę poza równoległą GV. W końcu cała
figura zajmie położenie podobne do pierwszego, tak że przy dalszym
obrocie i drugim kroku, bok większego wieloboku DC położy się na QX,
bok małego wieloboku KL, po przekroczeniu PX na YZ, a środek G,
poruszający się wciąż ponad GV, zejdzie tam dopiero w R, po wielkim
skoku CR. W rezultacie, większy wielobok, tocząc się po AS, odetnie
sześć linii równych jego obwodowi, bez żadnych przerw; wielobok
mniejszy pokryje również sześć jednakich odcinków, równych jego
obwodowi, ale poprzegradzanych pięcioma łukami, których cięciwy nie będą
dotknięte, stanowiąc części linii HT; wreszcie środek G w sześciu
punktach tylko schodzić się będzie z równoległą GV. Pojmujecie więc. że
przestrzeń HT, przebyta przez mały wielobok, jest prawie równą AS,
przebytej przez wielobok większy, od której jest mniejsza tylko o jedną
cięciwę małego łuku, uważając linię HT razem z pięcioma łukami.
Pragnąłbym teraz, aby to, co wam przedstawiłem na przykładzie tych
sześcioboków, okazało się wam również jasne przy innych wielobokach, z
dowolną liczbą boków, a tylko do siebie podobnych, współśrodkowych i
razem ze sobą związanych, tak że przy toczeniu się większych rozważać
można toczenie się mniejszych i że drogi przebyte są prawie równe, o
ile się dolicza przestrzenie pod łukami, nie dotknięte bokami
mniejszego wieloboku. Niech więc będzie większy wielobok o 1000 boków,
które odcinamy na przebytej przezeń drodze. Równocześnie mały wielobok
przebywa prawie tę samą drogę, dotknąwszy się 1000 małych odcinków,
przegrodzonych 1000 próżni, gdyż tak je możemy nazwać w przeciwieństwie
do 1000 odcinków dotkniętych. To, co powiedziałem, nie przedstawia żadnej
trudności ani wątpliwości. Ale powiedzcie mi, jeżeli około jakiego
środka np. A, zakreślimy dwa koła współśrodkowe, związane razem i jeżeli
z końców ich średnic C i B poprowadzimy dwie styczne CE, BF, a przez
środek A równoległą AD i jeżeli toczyć będziemy koło większe po BF (i
uczynimy BF równe obwodowi koła równie jak i linie CE i AD), to po
jednym obrocie cóż się stanie z małym kołem i ze środkiem? Ten ostatni
przebiegnie niewątpliwie całą długość AD, a obwód małego koła dotknie
się swymi punktami całej linii CE, w ten sam sposób jak to było
poprzednio z wielobokiem; z tą jedyną różnicą, że tam linia HT nie we wszystkich punktach była
dotykana przez mały wielobok, bo wiele małych odcinków było
przeskoczonych, tu zaś przy kole nie może jego obwód opuszczać ani na
chwilę linii CE i każdy jego punkt musi się na niej znajdować. W jaki
więc sposób może mniejsze koło, bez przeskakiwania, przebiec drogę tak
znacznie dłuższą od swego okręgu?
SAGREDO: Sądzę, że można by powiedzieć, że równie jak środek koła,
ciągniony po AD, dotyka się jej całej, jakkolwiek jest tylko jednym
punktem, tak samo punkty małego koła, pociągane ruchem koła większego,
mogą się prześlizgiwać po cząstkach linii CE.
SALVIATI: Nie może to mieć miejsca z dwóch przyczyn. Po pierwsze dlatego, że nie ma większego powodu utrzymywać, że dotykanie, podobne do
ślizgania się C, następuje na pewnej części linii CE, a na innej jej
części nie; gdyby zaś tak było, to musiałoby być nieskończenie wiele
takich zetknięć (bo punktów jest nieskończoność) i ślizgań byłoby także
nieskończenie wiele; a że każde ma pewną długość, to dałyby razem
długość nieskończoną, podczas gdy linia CE jest skończoną. Po wtóre dlatego, że wielkie koło, tocząc się, wciąż zmienia swój punkt zetknięcia,
a więc nie może go nie zmieniać i koło małe, bo nie można jak tylko z B
poprowadzić linii prostej do środka A, która by równocześnie przechodziła
przez C, tak że gdy wielkie koło zmienia swój punkt zetknięcia, to małe
czyni to samo, a żaden punkt małego koła nie dotknie więcej jak jednego
punktu prostej CE. Nadto, przy toczeniu się wieloboków, każdy punkt
małego obwodu przykłada się tylko do jednego punktu linii, która z tego
obwodu została wyprowadzona, jak się to widzi łatwo, zważywszy, że IK
jest równoległe do BC, a więc dopóki BC nie położy się na BQ, to linia
IK pozostaje wzniesiona ponad IP i nie prędzej na niej się kładzie aż
gdy BC padnie na BQ, a wtedy IK schodzi się z OP, ażeby się znów zaraz
podnieść.
SAGREDO: Przebieg jest istotnie bardzo ciekawy i nie widzę żadnego
rozwiązania, mówcie przeto, co uważacie za odpowiednie.
SALVIATI: Wracając do powyżej rozważanych wieloboków, których ruch
był zrozumiały i został pojęty, powiedziałbym, że jak przy wielobokach
o 100000 boków droga przebyta jest równa obwodowi większego
wieloboku, tj. owym 100000 boków ułożonym bez przerwy jeden za drugim
a także równa 100000 boków mniejszego, poprzegradzanych 100000 miejsc
pustych, - to tak samo przy kołach (które są wielobokami o nieskończonej
liczbie boków) linia opisana jest równa nieskończenie wielu bokom
wielkiego koła, w ciągłym następstwie i równa także nieskończenie wielu
bokom małego koła, poprzegradzanym takąż liczbą miejsc pustych. A
ponieważ liczba boków jest niezliczona, więc nieskończoną także jest
liczba przegradzających je miejsc pustych. Tam więc mamy nieskończenie
wiele punktów pełnych, a tu nieskończenie wiele punktów, częścią pełnych
a częścią pustych. I tutaj proszę zauważyć, że nie można, podzieliwszy
linię na skończone i dające się przeliczyć części, zebrać następnie tych
części w linię dłuższą od tej, jaką stanowiły przed podzieleniem, nie
poprzegradzawszy ich pustymi miejscami; ale, wyobraziwszy sobie linię,
podzieloną na nieskończenie wiele części nieskończenie małych, możemy z
nich złożyć linię nieskończenie długą, bez ich przegradzania
skończonymi miejscami pustymi a tylko nieskończenie małymi. l to, co
mówię o liniach, odnosi się także do powierzchni ciał stałych, jeżeli
te uważać będziemy jako złożone z nieskończonej liczby atomów; dzieląc
bowiem ciała na części skończone, niewątpliwie nie możemy złożyć z tych
części takich ciał, które by zajmowały większe przestrzenie niż ciała
pierwotne, bez przegradzania ich miejscami pustymi, tj. takimi, w
których się żadna część ciała stałego nie znajduje: ale,
jeżeli
wyobrazimy sobie największe i ostateczne podzielenie ciała na pierwotne
części składowe, tj. na nieskończenie wiele nieskończenie małych
cząstek, to moźna by z nich tworzyć bardzo wielkie ciała, bez
przegradzania skończonymi pustymi przestrzeniami, a tylko wstawiając
nieskończenie wiele nieskończenie małych miejsc pustych; w ten sposób
np. można małą kulkę złota rozciągnąć na bardzo wielką przestrzeń bez
przyjmowania skończonych miejsc pustych, jeżeli przyjmiemy, że złoto
składa się z nieskończonostek niepodzielnych.
SIMPLICIO: Zdaje mi się że jesteście na śladzie owych próżni
rozproszonych, pewnego starożytnego filozofa.
SALVIATI: Lecz nie dodajecie: tego filozofa, który przeczył
boskiej opatrzności, jak w podobnym przypadku zauważył, w sposób mniej
stosowny, przeciwnik naszego Akademika.
SIMPLICIO: Zauważyłem też, i nie bez oburzenia, niechęć źle
usposobionego przeciwnika, lecz nie tylko przez delikatność unikam
dotykania tych kwestii, a także dlatego, że wiem, jak mało one
odpowiadają waszemu umiarkowaniu i wysokiemu wykształceniu, gdyż
jesteście nie tylko religijni i pobożni, lecz także katolicy i
bogobojni. Ale, wracając do naszego zadania, znajduję jeszcze wiele
trudnych punktów w naszej rozmowie, z których prawdopodobnie nie będę
mógł wybrnąć. Przede wszystkiem, jeżeli oba obwody kół są równe obu
prostym CE, BF, tej ostatniej pełnej a tamtej ze wstawieniem
nieskończenie wielu pustych punktów, to w jaki sposób może być linia
AB, opisana przez środek, a więc przez jeden punkt, uważaną jako równa
zawierającym nieskończoności punktów? A przy tym, to tworzenie linii z
punktów, podzielnej z niepodzielnych, skończonej z nieskończonostek,
wydaje mi się twardym orzechem do zgryzienia; przyjęcie zaś próżni,
którą tak trafnie zbijał Arystoteles, prowadzi do tych samych trudności.
SALVIATI: Są one niewątpliwie a przy tym inne jeszcze, ale zwróćmy
uwagę na to, że znajdujemy się w dziedzinie nieskończenie wielkich i
najmniejszych niepodzielnych, jednych niedościgłych dla swej wielkości,
a drugich dla małości; widzimy stąd, że mowa ludzka nie wystarcza do
odpowiedniego ich wyrażenia; pozwolę sobie wszakże podać niektóre myśli,
które jeżeli nie wyczerpią całkowicie kwestii, to jednak zasłużą na
uwagę swą nowością: obawiam się jednak aby częste zbaczania z drogi nie
wydały się wam niepotrzebne, a przeto niezbyt przyjmne.
SAGREDO: Prosimy, pozwólcie
nam korzystać z dobrodziejstwa i przywileju rozmowy z żywymi i
przyjaciółmi, o rzeczach dowolnych a nie koniecznych, odmiennych od
tych, które są traktowane w martwych księgach, budzących tysiące
wątpliwości, z których żadna nie może być rozwiązana. Pozwólcie więc nam
brać udział w rozważaniach, które się wam nasuną w ciągu rozmowy; a nie
zbraknie nam czasu, gdyż żadne zajęcia obowiązkowe nie oderwą nas od
rozpraw i rozwiązywania poruszanych kwestji; zwłaszcza też należy
rozwiązać wątpliwości, jakie się nasuwały panu Simplicio.
SALVIATI: Niech więc tak będzie, skoro to wam przypada do gustu. A
najpierw spytajmy, w jaki sposób pojedynczy punkt może się stać równym
jednej linii. Nie widzę tu innego wyjścia, jak nieprawdopodobieństwo
złagodzić drugim, podobnym albo większym, tak jak często rzecz cudowna
zaćmiewa cud. Wyobraźcie sobie, że dwie równe powierzchnie, służące za
podstawy dwom równym bryłom, zaczynają się jedna i druga powoli i
równomiernie zmniejszać, w ten sposób wszakże, że nie przestają być
sobie równe w każdej chwili, aż w końcu jedna powierzchnia razem ze
swoją bryłą zejdzie do jednej bardzo długiej linii, a druga z bryłą
także zamieni się na jeden punkt, czyli, innymi słowy, z jednej mamy
punkt, a z drugiej nieskończenie wiele punktów.
SAGREDO: Rzecz ta wydaje się istotnie zadziwiająca, toteż prosimy o
objaśnienie i dowód.
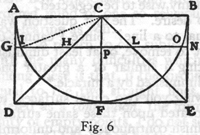 SALVIATI: Potrzeba do tego rysunku, gdyż dowód jest czysto
geometryczny. Niech będzie półkole AFB, ze środkiem w C, (rys.
6) i otaczający je prostokąt ADEB; poprowadzimy linie proste z C do
punktów D i E. Wyobraźmy sobie, że promień CF, prostopadły do AB i DE,
stoi nieruchomo, a cała figura obraca się wokół niego jako osi.
Oczywiście prostokąt ADEB opisze walec, półkole AFB - półkulę a trójkąt
CDE - ostrokrąg. Przypuśćmy następnie, że półkula zostanie wyjęta, a
pozostanie ostrokrąg i reszta cylindra, którą dla kształtu podobnego
do miski, nazwiemy poprostu miską; dowiedziemy najpierw, że miska i
ostrokrąg są równe; następnie, przeprowadziwszy płaszczyznę równoległą
do koła, będącego podstawą miski, którego średnicą jest DE a środkiem
F, dowiedziemy, że taka płaszczyzna, np. przechodząca przez GN,
przecina miskę według GION, a ostrokrąg według HL w ten sposób, że reszta
ostrokręgu CHL jest zawsze równa reszcie miski, której profil
przedstawiają trójkąty GAI, BON; okaże się dalej, że podstawa tego
ostrokręgu, tj. koło o średnicy HL, jest stale równe tej powierzchni
kołowej, która stanowi podstawę reszty miski, a którą nazwiemy wstęgą o
szerokości GI (zauważcie przy tym, jak są potrzebne określenia
matematyków, nadające nazwy albo, że tak powiem, skrócone sposoby
mówienia, zestawione i wprowadzone dla usunięcia kłopotliwego trudu,
który musielibyśmy ponosić, nie umówiwszy się nazwać np. owej
powierzchni - wstęgą kołową, a ostrego wierzchu miski - okrągłą brzytwą).
Jakkolwiek zresztą je nazwiecie, wystarczy przekonać się, że
płaszczyzna, poprowadzona w jakiejkolwiek odległości, ale równolegle do
podstawy, czyli do koła o średnicy DE, odetnie dwie bryły, zawsze równe
sobie: wierzch ostrokręgu CHL i wierzch brzytwy kołowej; a tak samo będą
sobie równe obie powierzchnie podstaw tych brył, tj. wspomniana
wstęga i koło HL. Wynika stąd zadziwiające twierdzenie, że, gdy
przypuścimy ciągłe podnoszenie się płaszczyzny przecinającej i jej
zbliżanie się do AB, to wciąż zarówno bryły odcięte, jak i powierzchnie
ich podstaw, będą sobie równe; aż w końcu tak obie bryły, jak i obie
powierzchnie zamienią się, jedne na koło a drugie na punkt, gdyż tym
jest dla jednych ostry brzeg miski, a dla drugich wierzchołek ostrokręgu.
Dalej, ponieważ przy ciągłym zmniejszaniu się obu brył utrzymuje się
stale wzajemna ich równość, przeto wnosić należy, że i ostatnie reszty
pozostaną sobie równe i nie będzie jedna nieskończenie większą od
drugiej: a więc obwód wielkiego koła może być przyrównany do jednego
punktu. A to samo, co się dzieje z bryłami, odnosi się również do ich
podstaw, które także, przy podnoszeniu się płaszczyzny przecinającej,
utrzymują wzajemną równość, aż się w końcu zamienią, równocześnie, jedna
na koło, a druga na punkt. I dlaczegóż nie mielibyśmy ich uważać za
równe, skoro są one ostatnimi resztami i śladami obu równych wielkości?
Zauważcie jeszcze, że gdyby miska była tak wielka, jak półkula nieba, to
i wtedy jej reszta byłaby równa wierzchołkowi ostrokręgu, chociaż
stanowi ją koło, będące obwodem sklepienia niebios, a wierzchołek
ostrokręgu jest tylko punktem. Na podstawie takich rozumowań twierdzimy,
że wszystkie okręgi kół, jakkolwiek są różne, mogą być nazwane równymi,
a każdy z nich równy jednemu punktowi.
SALVIATI: Potrzeba do tego rysunku, gdyż dowód jest czysto
geometryczny. Niech będzie półkole AFB, ze środkiem w C, (rys.
6) i otaczający je prostokąt ADEB; poprowadzimy linie proste z C do
punktów D i E. Wyobraźmy sobie, że promień CF, prostopadły do AB i DE,
stoi nieruchomo, a cała figura obraca się wokół niego jako osi.
Oczywiście prostokąt ADEB opisze walec, półkole AFB - półkulę a trójkąt
CDE - ostrokrąg. Przypuśćmy następnie, że półkula zostanie wyjęta, a
pozostanie ostrokrąg i reszta cylindra, którą dla kształtu podobnego
do miski, nazwiemy poprostu miską; dowiedziemy najpierw, że miska i
ostrokrąg są równe; następnie, przeprowadziwszy płaszczyznę równoległą
do koła, będącego podstawą miski, którego średnicą jest DE a środkiem
F, dowiedziemy, że taka płaszczyzna, np. przechodząca przez GN,
przecina miskę według GION, a ostrokrąg według HL w ten sposób, że reszta
ostrokręgu CHL jest zawsze równa reszcie miski, której profil
przedstawiają trójkąty GAI, BON; okaże się dalej, że podstawa tego
ostrokręgu, tj. koło o średnicy HL, jest stale równe tej powierzchni
kołowej, która stanowi podstawę reszty miski, a którą nazwiemy wstęgą o
szerokości GI (zauważcie przy tym, jak są potrzebne określenia
matematyków, nadające nazwy albo, że tak powiem, skrócone sposoby
mówienia, zestawione i wprowadzone dla usunięcia kłopotliwego trudu,
który musielibyśmy ponosić, nie umówiwszy się nazwać np. owej
powierzchni - wstęgą kołową, a ostrego wierzchu miski - okrągłą brzytwą).
Jakkolwiek zresztą je nazwiecie, wystarczy przekonać się, że
płaszczyzna, poprowadzona w jakiejkolwiek odległości, ale równolegle do
podstawy, czyli do koła o średnicy DE, odetnie dwie bryły, zawsze równe
sobie: wierzch ostrokręgu CHL i wierzch brzytwy kołowej; a tak samo będą
sobie równe obie powierzchnie podstaw tych brył, tj. wspomniana
wstęga i koło HL. Wynika stąd zadziwiające twierdzenie, że, gdy
przypuścimy ciągłe podnoszenie się płaszczyzny przecinającej i jej
zbliżanie się do AB, to wciąż zarówno bryły odcięte, jak i powierzchnie
ich podstaw, będą sobie równe; aż w końcu tak obie bryły, jak i obie
powierzchnie zamienią się, jedne na koło a drugie na punkt, gdyż tym
jest dla jednych ostry brzeg miski, a dla drugich wierzchołek ostrokręgu.
Dalej, ponieważ przy ciągłym zmniejszaniu się obu brył utrzymuje się
stale wzajemna ich równość, przeto wnosić należy, że i ostatnie reszty
pozostaną sobie równe i nie będzie jedna nieskończenie większą od
drugiej: a więc obwód wielkiego koła może być przyrównany do jednego
punktu. A to samo, co się dzieje z bryłami, odnosi się również do ich
podstaw, które także, przy podnoszeniu się płaszczyzny przecinającej,
utrzymują wzajemną równość, aż się w końcu zamienią, równocześnie, jedna
na koło, a druga na punkt. I dlaczegóż nie mielibyśmy ich uważać za
równe, skoro są one ostatnimi resztami i śladami obu równych wielkości?
Zauważcie jeszcze, że gdyby miska była tak wielka, jak półkula nieba, to
i wtedy jej reszta byłaby równa wierzchołkowi ostrokręgu, chociaż
stanowi ją koło, będące obwodem sklepienia niebios, a wierzchołek
ostrokręgu jest tylko punktem. Na podstawie takich rozumowań twierdzimy,
że wszystkie okręgi kół, jakkolwiek są różne, mogą być nazwane równymi,
a każdy z nich równy jednemu punktowi.
SAGREDO: Rozumowanie wydaje mi się tak piękne i cenne, że choćbym
mógł, nie chcę mu nic przeciwstawiać, bo byłoby świętokradztwem naruszyć
tę piękną budowę jakimś pedantycznym napadem, toteż dla zadowolenia nas
dajcie tylko dowód geometryczny stałej równości obu brył i ich podstaw;
nie jest on chyba zbyt trudny, a rozważanie filozoficzne było tak
subtelne, że od tego zależy wniosek ostateczny.
SALVIATI: Dowód jest łatwy i krótki. Wróćmy do naszego rysunku
(rys. 6), na którym kąt IPC jest prosty, kwadrat promienia IC
równy kwadratom dwóch boków IP, PC. Promień IC jest równy AC, a AC równe
GP, CP równe PH; a więc kwadrat z GP jest równy obu kwadratom z IP i PH
i poczwórne poczwórnemu, czyli kwadrat z GN równy kwadratom z I0 i HL;
że zaś powierzchnie kół mają się do siebie jak kwadraty średnic, więc
powierzchnia koła o średnicy GN jest równa dwom powierzchniom kół o
średnicach I0 i HL; odejmując po obu stronach powierzchnię koła o
średnicy I0, zostaje reszta powierzchni koła GN równa kołu o średnicy
HL. Oto co się tyczy pierwszej części. Co do drugiej, to tymczasem
pominiemy dowodzenie, bo dla naszego przypadku wystarcza, gdy
dowiedzieliście się, że wzmiankowane powierzchnie są zawsze równe i że
przy postepującym ich zmniejszaniu jedna zamienia się na punkt, a druga
na koło jakiejkolwiek wielkości, gdyż tylko ten wynik budził nasz
podziw.
SAGREDO: Piękny dowód odpowiada zadziwiającemu rozważaniu.
Powiedzcie nam coś teraz o drugiej kwestii, jaką podniósł p. Simplicio,
jeżeli macie co szczególnego do powiedzenia w tej sprawie, czego nie
przypuszczam, gdyż spór ten wielokrotnie był już rozstrząsany.
SALVIATI: Mam pewną myśl, ale najpierw przypomnę, co powiedziałem,
że nieskończoność sama przez się jest równie niezrozumiała, jak i
cząstki niepodzielne; bo popróbujcie je zestawić: jeżeli chcemy złożyć
linię z punktów niepodzielnych, to te ostatnie muszą być nieskończenie
małe, musimy więc jednocześnie badać nieskończoność i niepodzielność.
Przy podobnych zadaniach przedstawiły mi się różne punkty widzenia, z
których najważniejsze nie od razu przyszły mi na myśl, lecz dopiero
nasuwają się w trakcie rozmowy, gdy dochodzę do zarzutów wyrażonych
przez was, a zwłaszcza przez pana Simplicia, gdyż bez tej pobudki
pozostałyby we śnie mej fantazji. Toteż ze zwykłą swobodą pozwolę sobie
je przedstawić, gdy się wynurzą nasze ludzkie chimery, tak bowiem należy
je nazwać w porównaniu z wiedzą nadprzyrodzoną, jedyną prawdziwą,
rozwiązującą nasze kwestie sporne i służącą za pewnego przewodnika w
naszym ciemnym i niepewnym labiryncie myśli.
Główny zarzut czyniony tym, którzy tworzą ciągłość z
niepodzielnostek jest ten, że jedna niepodzielnostka, dodana do drugiej
nie daje wielkości podzielnej; gdyby bowiem tak było, wynikałoby stąd,
że i niepodzielnostka jest podzielna, bo skoro dwie niepodzielnostki
np. dwa punkty dają razem pewną ilość, stanowiącą linię podzielną, to
jeszcze więcej podzielna byłaby linia złożona z trzech, pięciu, siedmiu
lub innych wielkości nieparzystych; a podzielenie następnie każdej
takiej linii na dwie połowy przecięłoby na dwoje niepodzielnostkę leżącą
w środku. Tego, jak i innych podobnych zarzutów uniknąć można, mówiąc,
że nie tylko dwie, ale dziesięć, sto i tysiąc niepodzielnostek nie mogą
utworzyć wielkości podzielnej, lecz tylko gdy ich jest nieskończenie
wiele.
SIMPLICIO: Tu nasuwa się wątpliwość, jak mi się zdaje nierozwiązalna
i ponieważ właśnie możemy mieć linie nierównej długości, z których
każda składa się z nieskończenie wielu punktów, to musimy wnosić, że
wśród rzeczy jednego rodzaju znaleźć można jedną większą od
nieskończoności, bo nieskończoność punktów większej linii jest przecież
większa od nieskończoności punktów linii mniejszej. Będzie więc jedna
nieskończoność większa od drugiej, co wydaje mi się zupełnie
niezrozumiałe.
SALVIATI: Są to trudności, stąd powstające, że naszym skończonym
umysłem nie możemy rozważać nieskończoności, bo przypisujemy jej te
własności, które widzimy w rzeczach skończonych i ograniczonych a które
tu się nie nadają, bo pojęcia większości, mniejszości i równości nie
mogą być stosowane do nieskończoności i niepodobna mówić o większych,
mniejszych lub równych nieskończonościach. Nasuwa się przykład, który
przedstawię w zapytaniach do p. Simplicia, skoro on wzbudził dyskusję.
Przyjmuję najpierw, że wiadomo wam dobrze, które liczby są
kwadratami, a które nie.
SIMPLICIO: Wiem dobrze, że kwadratem jest iloczyn z pewnej liczby,
pomnożonej przez siebie samą, i tak 4, 9 są kwadratami z 2 i 3.
SALVIATI: Wybornie. Pamiętajcie również, że tak samo, jak iloczyny
noszą nazwę kwadratów, to czynniki, czyli liczby przez siebie mnożone
nazywane są bokami albo pierwiastkami; inne znów, nie składające się z
liczb przez siebie pomnożonych, nie są kwadratami.
Jeżeli więc powiem,
że wszystkie liczby, kwadraty i nie kwadraty, stanowią więcej niż same
kwadraty, to wszak wyrażam ścisłą prawdę?
SIMPLICIO: Nie mogę powiedzieć inaczej.
SALVIATI: Teraz jeżeli się zapytam, ile jest kwadratów, to można
słusznie odpowiedzieć, że tyle ile pierwiastków, bo każdy kwadrat ma
swój pierwiastek i każdy pierwiastek - swój kwadrat,
żaden kwadrat nie
ma więcej pierwiastków i żaden pierwiastek więcej kwadratów, jak tylko
jeden.
SIMPLICIO: Zupełna prawda.
SALVIATI: Ale jeżeli zapytam, ile jest pierwiastków, to
nie można
przeczyć, że są one równie liczne, jak cały szereg liczb, gdyż nie ma
liczby, która by nie była pierwiastkiem jakiegoś kwadratu. Skoro to jest
ustalone, to powiedzieć należy, że tyle jest kwadratów, ile liczb, gdyż
tyle jest kwadratów, ile pierwiastków, a pierwiastkami są wszystkie
liczby; a że, jak powiedziałem na początku, więcej jest liczb niż
kwadratów, to w większej swej części nie są one kwadratami. I
rzeczywiście im większe liczby bierzemy pod uwagę, tym bardziej zmniejsza
się wśród nich liczba kwadratów, bo do 100 mamy 10 kwadratów czyli 1/10,
do 10000 - 1/100, a do 1000000 - tylko 1/1000, a do liczby nieskończonej,
gdybyśmy mogli ją pomyśleć - musielibyśmy powiedzieć, że jest tyle
kwadratów, ile wszystkich liczb razem.
SAGREDO: Cóż więc robić, aby kwestię rozwiązać?
SALVIATI: Nie widzę innego wyjścia, jak powiedzieć: nieskończenie
wiele jest liczb, nieskończenie wiele kwadratów i nieskończenie wiele
pierwiastków. Wielość kwadratów nie jest ani większa ani mniejsza od
wielości liczb i w ostatecznym wniosku pojęcia równości większości i
mniejszości nie stosują się do nieskończoności, a tylko do ilości
skończonych. Toteż p. Simplicio przedstawia mi parę linii nierównych i
pyta, jak to być może, aby w większej nie było więcej punktów jak w
mniejszej, odpowiadam, że nie ma tam ani więcej, ani mniej, ani tyle
samo,
tylko w każdej jest nieskończenie wiele. I rzeczywiście, gdybym mu
odpowiedział, że jedna linia ma tyle punktów, ile jest kwadratów, druga
większa - ile liczb, a trzecia najmniejsza - ile sześcianów, nie byłbym
mu dał więcej zadowalającej odpowiedzi, przyznając jednej linii więcej
punktów niż innym, a jednak wszystkim nieskończenie wiele. Tyle, co się
tyczy pierwszej trudności.
SAGREDO: Proszę, zatrzymajcie się chwilę i pozwólcie mi dodać moje
myśli, które mi przychodzą do głowy. Zdaje mi się, że z tego, co było
powiedziane, wynika, że nie można twierdzić, ani aby jedna
nieskończoność była większa od drugiej, ani też aby nieskończoność
była większa od wielkości skończonej; bo gdyby jaka liczba nieskończona
była większa np. od miliona, to wynikałoby stąd, że przechodząc od
miliona do liczb coraz większych, dojść można do nieskończoności; tak
zaś nie jest: przeciwnie, jeżeli przechodzimy do liczb coraz większych,
tym więcej oddalamy się od nieskończenia; bo, im większe bierzemy
liczby, tym rzadsze między nimi są kwadraty, a w liczbie nieskończonej
nie może być mniej kwadratów niż wszystkich liczb; gdy więc
przechodzimy do coraz większych liczb, oddalamy się od liczby
nieskończonej.
SALVIATI: Wnioskujemy więc z waszego dowcipnego rozważania, że
właściwości: większość, mniejszość, równość, nie mają miejsca nie tylko
między nieskończonościami, ale także między nieskończonością a
skończonością.
Przechodzę teraz do innych rozważań. Ponieważ linia i wszelka
ciągłość jest podzielna na cząstki w dalszym ciągu podzielne, to nie
można przeczyć wnioskowi, że linia składa się z nieskończenie wielu
cząstek niepodzielnych, gdyż z jednego podziału i dalszych dzieleń bez
końca wynika, że cząstek jest nieskończenie wiele, bo inaczej dzielenie
musiałoby mieć swój koniec; a skoro wielość cząstek jest nieskończona,
a nie skończona, więc nieskończenie wiele skończonych wielkości tworzy
razem wielkość nieskończoną i tak
dochodzimy do ciągłości, złożonej z nieskończenie wielu czkąstek
niepodzielnych.
SIMPLICIO: Ale skoro możemy prowadzić dalej dzielenie na części skończone, to dlaczego wprowadzamy tam koniecznie
nieskończonostki.
SALVIATI: Właśnie ta możność dzielenia bez końca zmusza do tworzenia
całości z nieskończonostek. Bo aby uniknąć sporu, powiedzcie mi, czy,
według waszego mniemania, części ciągłości są skończone, czy
nieskończone.
SIMPLICIO: Utrzymuję, że są nieskończone i skończone, potencjalnie
nieskończone, aktualnie skończone. Pod »potencjalnie« rozumiem »przed
wszelkiem dzieleniem«; »aktualnie« znaczy »po dokonanym podziale«; bo
istotnie nie można sobie wyobrazić części wcześniej niż po podziale
dokonanym (lub naznaczonym); przedtem zaś są one potencjalne.
SALVIATI: Więc linia długości 20 cali nie może aktualnie zawierać 20
linii jednocalowych, póki nie zostanie na 20 części podzielona, a
przedtem zawiera je tylko potencjalnie! A zresztą niech i tak będzie,
ale powiedzcie mi też, czy wskutek aktualnego dokonania podziału wzrasta
długość danej linii, czy się zmniejsza, czy też pozostaje niezmieniona?
SIMPLICIO: Ani się powiększa, ani zmniejsza.
SALVIATI: l ja tak myślę. A więc części pewnej ciągłości,
potencjalne lub aktualne, nie czynią całości większą lub mniejszą; lecz jest rzeczą jasną, że części skończone zawarte są aktualnie w
swej całości, a gdy ich jest nieskończenie wiele, to całość będzie
nieskończenie wielką; a więc części skończone, choćby tylko
potencjalnie było ich nieskończenie wiele, nie mogą utworzyć innej
całości, jak tylko nieskończoną; wynika stąd, że wielkość skończona nie
może się składać, aktualnie czy też potencjalnie, z nieskończenie wielu
części.
SAGREDO: Jakże więc może to być prawdziwe, że ciągłość może być
nieustannie dzielona na części, które znów dają się dzielić.
SALVIATI: Bo to rozróżnianie aktualności i potencjalności, czyni dla
nas możliwym to, co dla innych wydaje się niemożliwe. Ale ja pragnę
lepiej to rozwiązać, inaczej rozumując i na pytanie: czy części ograniczonej całości są skończone, czy nieskończone, dam
odpowiedź wprost przeciwną tej, jaką dał p. Simplicio, a mianowicie, że
nie są ani skończone, ani nieskończone.
SIMPLICIO: Nie umiałbym tak odpowiedzieć, gdyż nie znam żadnego
pojęcia pośredniego między »skończonym« a »nieskończonym« i
utrzymywanie, że jakaś rzecz może być albo skończoną albo nieskończoną
byłoby niesłuszne i wątpliwe.
SALVIATI: A mnie się zdaje, że tak jest. Jeżeli mowa o wielkościach
niestałych, to zdaje mi się, że między skończonym a nieskończonym jest
jeszcze coś trzeciego, pośredniego, a mianowicie to, co odpowiada
każdej danej liczbie; tak że w danym przypadku na pytanie: czy części
pewnej całości są skończone czy nieskończone, najlepsza byłaby
odpowiedź, że nie są ani skończone ani nieskończone, lecz odpowiadające
każdej danej liczbie; aby tak było, nie może się ich tam znajdować
liczba ograniczona, bo w takim razie nie mogłyby odpowiadać liczbie
większej; ale znów nie trzeba, aby ich było nieskończenie wiele, gdyż
liczba ich jest dana i ta liczba nie może być nieskończenie wielką. I
tak, możemy, stosownie do woli pytającego, przyznać danej linii 100,
1000, 10000 części skończonych, lecz nie można jej podzielić na
nieskończenie wiele części. Godzę się więc z panami filozofami, że
ciągłość zawiera tyle części, ile się im podoba i dodaję, że zawiera je
aktualnie lub potencjalnie, według ich gustu i upodobania; nadmieniam
wszakże, że tak samo jak w linii dziesięciołokciowej mieści się
dziesięć linii łokciowych, dwadzieścia półłokciowych a czterdzieści
ćwierćłokciowych, to również mieści ona w sobie nieskończenie wiele
punktów; nazwijcie je aktualnymi lub potencjalnymi, jak chcecie, co do
mnie, składam się w tym względzie panie Simplicio na wasz pogląd i sąd.
SIMPLICIO: Nie mogę nie pochwalić waszego rozważania, lecz mam wielką
obawę, że to równoczesne zawieranie punktów i części skończonych nie
jest zupełnie ścisłe; toteż nie będzie wam tak łatwo podzielić danej
linii na nieskończenie wiele punktów, jak owym filozofom na 10 łokci lub
40 ćwiercłokci; wreszcie wydaje mi się niemożliwe doprowadzenie do
skutku takiego podziału, tak że to będzie czynność potencjalna, a nie
może się stać aktualną.
SALVIATI: Skoro rzecz jest tak trudna i tylko z trudem i
mozołem może być w ciągu długiego czasu przeprowadzona, to przez to
jeszcze nie jest niemożliwa, gdyż sądzę, że nie możecie równie łatwo
podzielić linii na 1000, na 937 albo na inną pierwszą liczbę części.
Lecz jeżeli ten podział, uważany przez was za niemożliwy, sprowadzę do
krótkiej czynności, tak prostej, jak podział na 40 części, czy wtedy go
przyjmiecie?
SIMPLICIO: Ten sposób postępowania przypadłby mi do gustu; a na
pytanie wasze mogę tylko odpowiedzieć, że ułatwienie będzie już wielkie,
jeżeli poprzestaniemy na podziale na 1000 części.
SALVIATI: Teraz powiem wam rzecz, która was zadziwi: jeżeli ktoś chce
podzielić linię na nieskończenie wiele punktów i spodziewa się dokonać
to w ten sposób, jak ów, który chciał otrzymać 10, 60 albo 100 części,
tj. jeżeliby dzielił najpierw na dwie części, potem na cztery itd., to
się grubo pomyli, bo tak postępując musiałby wiecznie dzielić; tymczasem
tą drogą nie można dojść do niepodzielnostek, gdyż się właśnie od nich
oddala; ciągnąc dalej dzielenie i powiększając liczbę części w nadziei
zbliżania się do nieskończoności, oddalamy się od niej, a to z tej
przyczyny. Z rozmowy przed chwilą wywiedliśmy wniosek, że liczba
nieskończona mieści w sobie tyle kwadratów i sześcianów, ile liczb, bo
kwadratów i sześcianów jest tyle, ile pierwiastków, a pierwiastkami są
wszystkie liczby. Widzieliśmy przy tym, że im większe bierzemy liczby,
tym mniej wśród nich jest kwadratów: jasne więc jest, że im do większych
liczb dochodzimy, tym więcej się oddalamy od nieskończoności, skąd
wynika, że jeżeli która liczba posiadać może właściwości (atrybuty)
nieskończoności, to właśnie jednostka. l rzeczywiście, w jednostce
znajdujemy warunki i konieczne atrybuty nieskończoności, a mianowicie zawiera ona tyle kwadratów i sześcianów, ile
liczb.
SIMPLICIO: Nie zdaję sobie sprawy, jak to należy rozumieć.
SALVIATI:
Rzecz jest niewątpliwa, bo jedność jest kwadratem, sześcianem, czwartą
potęgą itd. a kwadraty i sześciany nie mają żadnej własności, jakiej by
nie posiadała jedność, jak np. własność, że dwa kwadraty mają zawsze
między sobą liczbę średnioproporcjonalną. Weźcie jakikolwiek kwadrat i
jedność, a znajdziecie między nimi zawsze średnią-proporcjonalną.
Między 9 i 1 mamy 3, między 4 i 1 mamy 2, między 9 i 4 mamy 6. Sześciany
mają między sobą dwie średnie proporcjonalne np. 8 i 27 mają 12 i 18, 1
i 8 mają 2 i 4, 1 i 27 mają 3 i 9. Wnioskujemy stąd, że nie ma innej
liczby nieskończonej jak jednostka. Są to rzeczy godne podziwu
i
przekraczające pojętność naszego umysłu; uczą nas one, jak
 bardzo się
mylimy, przypisując nieskończoności tż same własności co ilości
skończonej, podczas gdy te własności nie mogą się odnosić równocześnie
do obu. Dodam tu jeden zadziwiający przypadek, który przychodzi mi na
myśl, wykazujący niezmierną różnicę między tymi ilościami, oraz
sprzeciw a niemal wstręt natury do przeprowadzenia wielkości skończonej
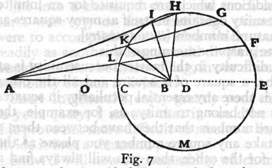
w nieskończoną. Niech będzie jakakolwiek linia AB (rys. 7);
punkt C dzieli ją na dwie części nierówne: jeżeli z końców A i B
zataczać będziemy koła promieniami proporcjonalnymi do długości AC i
CB, to te koła przecinać się będą ze sobą w punktach leżących na
obwodzie jednego i tegoż samego koła, np. jeżeli AL : LB = AC : CB i AK
: KB = AI : IB = AC : AB itd., to punkty przecięć C L K I H G F E leżą wszystkie na
obwodzie tegoż samego koła, tak że można powiedzieć, iż skoro punkt C
tak się porusza, że jego odległości od A i B pozostają do siebie zawsze
w tym samym stosunku, to ruchem swym opisuje koło. Koło to będzie tym
większe, im punkt C jest bliższy środka O linii AB, a tym mniejsze, im C
leży bliżej B, tak że z pomiędzy nieskończenie wielu punktów, które
można wybrać między O i B, otrzymać można koła różnej wielkości, w
końcu tak małe, jak oko pchły, ale także tak wielkie, jak równik kuli
niebieskiej (del primo Mobile). Każdy punkt między O i B da koło bardzo
wielkie w pobliżu O, a zbliżając się w dalszym ciągu
do O, tak że C zejdzie się z O, jaką linię otrzymamy przy zachowaniu
pierwotnego stosunku odległości od A i B? Może okrąg koła większy od
wszelkich największych, koło nieskończonej wielkości. Ale jednocześnie
będzie to linia prosta, prostopadła do AB, przez punkt O, nieskończenie
długa i nie zakrzywiająca się na końcach, tak żeby się złączyły, jak to
miało miało miejsce z innymi liniami, bo półkole górne CHE łączyło się
z dolnym EMC. Ale przez punkt O przechodzi koło największe ze
wszystkich (gdyż wszystkie punkty z drugiej strony OA dają koła tym
większe, im bliżej leżą O), a więc nieskończenie wielkie i to koło nie
może się już zaginać i wracać do swego punktu wyjścia i
stanowi linię
prostą, jako okrąg nieskończenie wielki. Rozważcie teraz, jaka jest
różnica między kołem skończonym a nieskończenie wielkim, tak zmienia
ono swą istotę, że przestaje być kołem: dodam jeszcze, że nie może
istnieć żadne koło nieskończone, a zatem i żadna kula nieskończona, ani
jakiekolwiek nieskończone ciało lub powierzchnia. Cóż więc powiedzieć
możemy o podobnych przemianach rzeczy skończonych na nieskończone? I
dlaczego mielibyśmy się oburzać, gdyśmy przy szukaniu nieskończoności
wśród liczb znaleźli w końcu jedność? Jeżeli po rozbiciu ciała stałego
na wiele części zamienimy je na jak najdrobniejszy proszek, dochodząc do
jego nieskończenie małych składników (infiniti suoi atomi), które są już
niepodzielne, to dlaczego nie mamy powiedzieć, że ciało wróciło do
jednej ciągłości, może do stanu płynnego, jak woda, rtęć lub ten
sam metal stopiony? Czyż nie widzimy, że kamienie topią się na szkło, a
to samo szkło w silnym ogniu staje się płynniejsze od wody.
bardzo się
mylimy, przypisując nieskończoności tż same własności co ilości
skończonej, podczas gdy te własności nie mogą się odnosić równocześnie
do obu. Dodam tu jeden zadziwiający przypadek, który przychodzi mi na
myśl, wykazujący niezmierną różnicę między tymi ilościami, oraz
sprzeciw a niemal wstręt natury do przeprowadzenia wielkości skończonej
w nieskończoną. Niech będzie jakakolwiek linia AB (rys. 7);
punkt C dzieli ją na dwie części nierówne: jeżeli z końców A i B
zataczać będziemy koła promieniami proporcjonalnymi do długości AC i
CB, to te koła przecinać się będą ze sobą w punktach leżących na
obwodzie jednego i tegoż samego koła, np. jeżeli AL : LB = AC : CB i AK
: KB = AI : IB = AC : AB itd., to punkty przecięć C L K I H G F E leżą wszystkie na
obwodzie tegoż samego koła, tak że można powiedzieć, iż skoro punkt C
tak się porusza, że jego odległości od A i B pozostają do siebie zawsze
w tym samym stosunku, to ruchem swym opisuje koło. Koło to będzie tym
większe, im punkt C jest bliższy środka O linii AB, a tym mniejsze, im C
leży bliżej B, tak że z pomiędzy nieskończenie wielu punktów, które
można wybrać między O i B, otrzymać można koła różnej wielkości, w
końcu tak małe, jak oko pchły, ale także tak wielkie, jak równik kuli
niebieskiej (del primo Mobile). Każdy punkt między O i B da koło bardzo
wielkie w pobliżu O, a zbliżając się w dalszym ciągu
do O, tak że C zejdzie się z O, jaką linię otrzymamy przy zachowaniu
pierwotnego stosunku odległości od A i B? Może okrąg koła większy od
wszelkich największych, koło nieskończonej wielkości. Ale jednocześnie
będzie to linia prosta, prostopadła do AB, przez punkt O, nieskończenie
długa i nie zakrzywiająca się na końcach, tak żeby się złączyły, jak to
miało miało miejsce z innymi liniami, bo półkole górne CHE łączyło się
z dolnym EMC. Ale przez punkt O przechodzi koło największe ze
wszystkich (gdyż wszystkie punkty z drugiej strony OA dają koła tym
większe, im bliżej leżą O), a więc nieskończenie wielkie i to koło nie
może się już zaginać i wracać do swego punktu wyjścia i
stanowi linię
prostą, jako okrąg nieskończenie wielki. Rozważcie teraz, jaka jest
różnica między kołem skończonym a nieskończenie wielkim, tak zmienia
ono swą istotę, że przestaje być kołem: dodam jeszcze, że nie może
istnieć żadne koło nieskończone, a zatem i żadna kula nieskończona, ani
jakiekolwiek nieskończone ciało lub powierzchnia. Cóż więc powiedzieć
możemy o podobnych przemianach rzeczy skończonych na nieskończone? I
dlaczego mielibyśmy się oburzać, gdyśmy przy szukaniu nieskończoności
wśród liczb znaleźli w końcu jedność? Jeżeli po rozbiciu ciała stałego
na wiele części zamienimy je na jak najdrobniejszy proszek, dochodząc do
jego nieskończenie małych składników (infiniti suoi atomi), które są już
niepodzielne, to dlaczego nie mamy powiedzieć, że ciało wróciło do
jednej ciągłości, może do stanu płynnego, jak woda, rtęć lub ten
sam metal stopiony? Czyż nie widzimy, że kamienie topią się na szkło, a
to samo szkło w silnym ogniu staje się płynniejsze od wody.
SAGREDO: Mamy więc uważać płyny za takie dlatego, że są rozłożone na
nieskończenie małe niepodzielne swoje składniki?
SALVIATI: Nie umiem znaleźć lepszego sposobu objaśnienia niektórych
zjawisk, między nimi następującego: jeśli wezmę ciało twarde jak kość,
kamień, lub metal i młotkiem lub najdelikatniejszym pilnikiem podzielę
je na jak można najdrobnieszy proszek, to jasną jest rzeczą, że
najmniejsze cząsteczki, jakkolwiek każdej z nich oddzielnie nie możemy
ująć ani wzrokiem, ani dotykiem, są jeszcze skończone, ukształtowane i
zliczalne; gdy je skupimy, trzymają się razem, a gdy w tej kupce zrobimy
otwór, to ten pozostaje niezapełniony przez cząstki otaczające; skoro
zaś wszystko poruszymy i wstrząśniemy, otwór się zapełni, zaraz po
usunięciu ruchadła. To samo zjawisko widzimy gromadząc większe ciałka,
wszelkiego kształtu, nawet kuliste jak proso, zboże, śrut ołowiany lub
inne materiały. Gdy wszakże podobne zjawisko obserwujemy na wodzie, to
widzimy, że ta, podniesiona, natychmiast wyrównuje swą powierzchnię,
jeżeli na to pozwala naczynie lub ruchadło, to zrobione wgłębienie zaraz
się zapełnia, a dłużej poruszana waha się i szeroko rozpościera swe
fale. Wnioskować stąd należy słusznie, jak mi się zdaje, że najmniejsze
cząstki, z których woda jest złożona (gdyż są one mniejszej konsystencji
od najdrobniejszego proszku, jeżeli nie bez żadnej konsystencji) są
czymś innym od cząstek najmniejszych, skończonych i podzielnych; i nie
umiem znaleźć innej różnicy, jak tylko, że są niepodzielne. Zdaje mi się
też, że wyborna przejrzystość wody nie zbija tego nader pewnego
przypuszczenia, bo jeżeli weźmiemy najprzezroczystszy kryształ i
zaczniemy go tłuc, ubijać i proszkować, to straci swą przezroczystość i
to tym więcej, im drobniej został sproszkowany; a woda, choćby
najzupełniej sproszkowana, jest jeszcze zupełnie przezroczysta. Złoto i
srebro, więcej rozdrobnione kwasami (acqua forte) niż jakimkolwiek
pilnikiem, pozostają jednak proszkiem, a nie stają się płynem; bo one
topnieją dopiero wtedy, gdy cząstki niepodzielne ognia albo promieni
słońca je rozpuszczą, jak sądzę, na ich ostateczne składniki
niepodzielne.
SAGREDO: To co Waszmość zauważył przed chwilą odnośnie
światła, obserwowałem z podziwem i widziałem często, jak z pomocą
zwierciadła wklęsłego, trzycalowej średnicy, można w jednej chwili
stopić ołów; doszedłem też do wniosku, że gdyby zwierciadło było bardzo
wielkie, gładkie i parabolicznego kształtu, stopiłoby również każdy inny
metal w jak najkrótszym czasie, skoro niewielkie kuliste i niezbyt
wygładzone z taką siłą topiło ołów i zapalało wszelkie paliwo; uczyniło
mi to wiarogodnymi cuda zwierciadeł Archimedesa.
SALVIATI: Co do zwierciadeł Archimedesa, to uważam, że ich cudowność
jest godna wiary, jak ją opisuje wielu autorów; pisma samego Archimedesa
czytałem z niezmiernym podziwem i studiowałem, a gdybym miał jeszcze
jaką wątpliwość, to usunąłby ją wykład o zwierciadle palącym Bonaventury Cavaleri, który z lubością przeczytałem.
SAGREDO: I ja to dzieło miałem w ręku i czytałem z
przyjemnością i wielkim podziwem, a ponieważ znałem już autora, to
umocniłem się w przekonaniu, jakie miałem o nim, że jest jednym z
najznakomitszych matematyków naszego czasu. Lecz wracając do działania
promieni słonecznych i topienia metali, czyż mamy sądzić, że te
działania tak gwałtowne odbywają się bez ruchu, czy też z ruchem bardzo
szybkim?
SALVIATI: Inne ognie i topienia widzieliśmy dokonywane z ruchem i to
jak najszybszym: Tu należą działania piorunów, prochu w minach i
petardach, a zwłaszcza ta szybkość, z jaką płomień węgla, rozdmuchany miechem, zmieszany z gęstymi gazami, zwiększa
siłę topienia metali. Toteż nie mogę pojąć, aby działanie światła,
choćby najczystszego, odbywać się mogło bez ruchu i to jak najszybszego.
SAGREDO: Ale jaka jest prędkość światła i za jak wielką mamy ją
poczytywać? Czy to jest zjawisko chwilowe, nagłe, czy jak inne ruchem w
czasie? czy nie moźna by tego zbadać doświadczalnie?
SIMPLICIO: Codzienne doświadczenie uczy, że rozchodzenie się światła
jest momentalne. Gdy na znacznej odległości strzela artyleria, blask płomienia dochodzi do oka momentalnie, podczas gdy
huk do ucha dopiero po pewnym czasie.
SAGREDO: Eh!, panie Simplicio,
z tego codziennego doświadczenia
wynika tylko, że dźwięk potrzebuje więcej czasu niż światło, aby do
nas doszedł, ale nie dowodzi ono, że światło dochodzi momentalnie, a nie
bardzo szybko. l inna podobna obserwacja nie uczy więcej: gdy tylko
słońce pojawia się nad poziomem, spostrzegamy jego promienie, ale kto
nas zapewni, że te promienie nie były już nad poziomem wcześniej, nim
doszły do naszych oczu.
SALVIATI: Niedostatecznie przekonujący wynik tej i innych podobnych
obserwacji nasuwa na myśl, czy nie moźnaby jakim sposobem, bez błędu,
wykazać, czy iluminacja tj. rozchodzenie się światła jest istotnie
momentalne; bo już samo szybkie rozchodzenie się głosu pozwala
przypuszczać, że prędkość światła musi być jeszcze większa.
Próba, którą
sobie przypominam, była następująca: dwie osoby trzymały każda zapaloną
latarkę, lub inne światło, które każda mogła ręką zakrywać i
odsłaniać, jedna dla oczu drugiej; umieszczone były naprzeciwko siebie w
niewielkiej odległości i odsłaniały i zasłaniały światło, jedna dla
oczu drugiej tak, że gdy jedna zobaczyła odsłaniające się światło u
drugiej, zaraz odsłaniała swoje; taka korespondencja wzajemna
powtarzana była wielokrotnie, tak że wkrótce bez pomyłki, po
odsłonięciu jednego światła następowało odsłonięcie drugiego.
Wprawiwszy się na małej odległości, oddalali się od siebie
eksperymentatorzy, ze swymi światłami na duże, do trzech mil jeden od
drugiego; a przeprowadzając doświadczenie w nocy, zwracali baczną
uwagę, czy powtarzanie się znaków odbywa się w tym samym tempie u obu,
z czego można było wnioskować na pewno o momentalnym rozchodzeniu się
światła; gdyby bowiem światło rozchodziło się w czasie, to na
trzymilowej odległości, a więc na przestrzeni sześciu mil tam i
z powrotem, winny by się były wyraźnie uwidocznić opóźnienia. Gdyby zaś
chciano obserwować na jeszcze większej odległości, ośmiu lub dziesięciu
mil, moźna by użyć teleskopów, umieszczając eksperymentatorów w nocy,
ze światłami, w takich miejscach, w których światło, jedno drugiemu
gołem okiem niewidzialne, teleskopem może być dostrzeżone.
SAGREDO: Doświadczenie wydaje mi się nie mniej pewne, jak dowcipne,
ale powiedzcie mi, jaki z jego wykonania wyciągnęliście wniosek.
SALVIATI: Co prawda, doświadczenie robiłem tylko
w małej odległości,
mniejszej od mili, toteż nie mogłem się przekonać, czy istotnie
pojawienie się przeciwległego światła było momentalne; lecz, jeżeli światło nie jest momentalne, to prędkość jego jest
znaczna, tak że może być przyrównana do ruchu, jaki widzimy w
jasności błyskawicy, między chmurami odległemi na osiem do dziesięciu
mil; odróżniamy tam początek, nawet źródło, w pewnym oznaczonem miejscu
między chmurami; a choć bezpośrednio potem następuje największe
rozszerzenie jasności w okolicznych chmurach, wydaje mi się jednak, że
następuje w ciągu pewnego czasu, bo gdyby rozjaśnienie następowało
od razu w całości, a nie stopniowo, trudno by nam było odróżnić jego
początek, powiedziałbym środek, od brzegów i ostatecznego rozszerzenia.
Lecz w jaką otchłań niepewności zabrnęliśmy niebaczni, przez próżnie,
nieskończonostki, niepodzielne, ruchy momentalne, aby po tysiącznych
rozprawach nie móc dopłynąć do brzegu.
SAGREDO: Istotnie nie odpowiada to naszym zamiarom. Nieskończoność,
poszukiwana między liczbami, zdawała się mieścić w pojęciu jedności; z
niepodzielnostki rodziła się zawsze podzielność; próżnia wiązała się
niepodzielnie z pełnią; poglądy nasze błąkały się tak dalece, że koło
stawało się nieskończenie długą linią prostą, co, jeśli dobrze pamiętam,
miał nam p. Salviati stwierdzić matematycznem dowodzeniem. Przeto
jeżeli łaska podajcie nam je bez rozpraw.
(...)
SALVIATI: Jeżeli zgęszczenie i rozrzedzenie są przeciwnemi sobie
ruchami, to gdy widzimy olbrzymie rozrzedzenie, nie możemy przeczyć
niemniej wielkiemu zgęszczeniu; lecz olbrzymie rozrzedzenie i, co
więcej godne uwagi, prawie momentalne, widzimy codziennie. Czyż to nie
jest olbrzymie rozrzedzenie, gdy mała ilość prochu strzelniczego daje
niezmierzoną masę ognia? A czy czym innym jest nieskończone prawie
rozchodzenie się światła? A co by to było za zgęszczenie, gdyby połączyć
razem ten ogień i to światło, co przecież nie wydaje się niemożliwe, i
zamknąć je następnie w małej przestrzeni. Pomyślcie tylko, a znajdziecie
tysiące podobnych zjawisk rozrzedzenia, bo te częściej się zdarzają niż
zgęszczenie; bo gęstą materję częściej się ma pod ręką i łatwiej
podpada ona pod zmysły, czy to, gdy bierzemy drzewo i widzimy, jak się
ono rozrzedza na ogień i światło, a nie możemy zobaczyć ognia i światła
zgęszczających się na drzewo, czy też, gdy owoce i kwiaty i tysiące
innych podobnych ciał rozrzedzają się na zapachy, a nie możemy
obserwować atomów zapachu zgęszczających się na wonne ciała. Wszakże
brak rozumnej obserwacji zastąpić trzeba rozważaniem, które wystarczy
do zrozumienia nie tylko ruchu rozrzedzania i rozpuszczania się ciał
stałych ale także zgęszczania substancji delikatnych, choćby jak
najrzadszych. Badajmy więc, jak dokonywane być może zgęszczanie i
rozrzedzanie ciał bez pomocy próżni i przenikania; z czego nie wynika,
aby w naturze nie było ciał, przy których nie następują te zjawiska i
przy których to, co się Warn wydaje niemożliwe, istotnie się nie
zdarza. Wreszcie, panie Simplicio, na przekór Waszym filozofom
namęczyłem się rozważaniem, jak można pomyśleć zgęszczanie i
rozrzedzanie, nie przyjmując przenikania ciał i nie wprowadzając
próżni, zdarzeń, którym przeczycie i które odrzucacie, podczas kiedy,
gdybyście się na nie zgadzali, nie oponowałbym Warn tak stanowczo. Albo
więc usuńcie te niedogodności, albo zgódźcie się na moje rozważania, lub
wreszcie znajdźcie więcej odpowiednie.
SAGREDO: Przenikania, zgodnie z filozofami perypytetycznymi,
zupełnie przeczę. Co do próżni, to pragnąłbym rozstrząsnąć dowodzenie
Arystotelesa, którym on ją zwalcza, wbrew Waszemu i p. Salviati'ego
poglądowi. Proszę pana, p. Simplicio, podać nam dowodzenie filozofów, a
pan p. Salviati zechce łaskawie odpowiedzieć.
SIMPLICIO: Arystoteles, o ile sobie przypominam, występuje przeciwko
poglądowi niektórych dawnych filozofów, którzy próżnię wprowadzają jako
potrzebną do ruchu, utrzymując, że bez niej ruch nie mógłby powstać.
Przeciwstawiając się temu, Arystoteles dowodzi, że właśnie tworzenie
się ruchu sprzeciwia się przyjmowaniu próżni, a dowodzenie jego jest
następujące. Rozważa dwa przypadki: najpierw daje się poruszać dwom
różnym masom w jednym i tym samym ośrodku, a następnie jednej i tej
samej masie w dwóch różnych ośrodkach. W pierwszym przypadku utrzymuje,
że różne ciała poruszają się w tym samym ośrodku z różnymi
prędkościami, mianowicie proporcjonalnymi do ciężkości, tak że np.
dziesięć razy większy ciężar porusza się dziesięć razy prędzej. W drugim
przypadku przyjmuje, że prędkości tej samej masy w różnych ośrodkach
mają się do siebie w stosunku odwrotnym gęstości ośrodków, tak że np.
jeżeli gęstość wody jest dziesięć razy większa od gęstości powietrza, to
prędkość w powietrzu będzie dziesięć razy większa niż w wodzie. Drugi
pogląd tak się wywodzi: ponieważ rzadkość próżni różni się tylko o ilość
nieskończenie małą od rzadkości przestrzeni wypełnionej jak
najsubtelniejszą materią, to każde ciało, potrzebujące pewnego czasu do
ruchu w ośrodku pełnym, w próżni poruszać się powinno momentalnie, że zaś
ruch momentalny jest niemożliwy, żaden więc ruch w próżni nie może się
odbywać.
SALVIATI: Jest to, jak widzimy, dowodzenie ad
hominem, tj. skierowane przeciwko tym, którzy uważają, że próżnia jest
potrzebna dla ruchu. Jeżeli zgodzę się na wniosek,
bo i ja uważam, że
ruch nie odbywa się w próżni, to jednak przez to przyjmowanie próżni w
absolutnym znaczeniu nie może być porzucone. Aby powiedzieć coś po
myśli dawnych filozofów i lepiej przejrzeć, jak wiele Arystoteles
dowiódł, można by, zdaje mi się, odrzucić oba przykłady.
Wątpię najpierw
bardzo, czy Arystoteles sprawdził doświadczalnie, że dwa kamienie, z
których jeden jest dziesięć razy cięższy od drugiego, puszczone
równocześnie z wysokości stu łokci, spadają w ten
sposób, że, gdy pierwszy doszedł do ziemi, to drugi przeleciał dopiero
dziesięć łokci.
SIMPLICIO: Z przedstawienia waszego widzi się, że wykonywaliście to
doświadczenie, inaczej nie mówilibyście o sprawdzaniu.
SAGREDO: Ale ja, panie Simplicio, który nie wykonywałem
doświadczenia, zapewniam Was, że kula armatnia, 100, 200 lub więcej
funtowa, spadając, ani na cal nie wyprzedzi półfuntowej kuli strzelby,
spadającej równocześnie z tej samej wysokości 200 łokci.
SALVIATI: Bez żadnych doświadczeń, możemy krótkim a ścisłym wywodem
wykazać jasno, że jest niemożliwe, aby większy ciężar poruszał się
prędzej niż mniejszy, jeżeli oba są z jednej materii i wreszcie takie, o
jakich mówi Arystoteles. Więc powiedz, panie Simplicio, czy godzisz się
na to, że każde ciało spadające nią prędkość przez naturę oznaczoną,
tak że, aby się ta powiększała lub zmniejszała, potrzeba użyć siły
przyspieszającej lub opóźniającej.
SIMPLICIO: Niewątpliwie każde ciało ma w danym ośrodku prędkość
oznaczoną przez naturę, którą tylko nowy impet (impeto) może powiększyć, a nowa
przeszkoda zmniejszyć.
SALVIATI: Gdybyśmy więc mieli dwa ciała, których naturalne prędkości
są różne, to jasne jest, że gdy powolniejsze złączymy z prędszym, to
wtedy to ostatnie będzie opóźniane przez tamto, a powolniejsze będzie
przyspieszone przez prędsze. Czy zgadzacie się co do tego ze mną?
SIMPLICIO: Zdaję mi się, że to nastąpić winno niewątpliwie.
SALVIATI: Jeżeli więc jest prawdą, że wielki kamień porusza się z
prędkością ośmiu stopni a mniejszy z prędkością czterech stopni, to te
dwa kamienie złączone razem będą miały prędkość mniejszą od ośmiu
stopni. Ale połączone dwa kamienie są większe od wielkiego kamienia,
który miał prędkość ośmiu stopni, więc w tym razie ciężar większy
poruszałby się wolniej od mniejszego, co sprzeciwiałoby się Waszemu
założeniu. Widzicie więc jak z założenia, że większe ciało porusza się
prędzej od mniejszego, dochodzę do wniosku, że większy ciężar porusza
się wolniej.
SIMPLICIO: Jestem zupełnie stropiony, gdyż wydaje mi się teraz, że
mały kamień, dołączony do większego, powiększa jego ciężar, gdy
tymczasem ten ciężar nie zostanie powiększony zarówno, jak i prędkość, a
w każdym razie ta ostatnia się nie zmniejsza.
SALVIATI: Tu popełnia pan nowy błąd, panie Simplicio, gdyż nie jest
prawdą, aby mały kamień powiększał ciężar większego.
SIMPLICIO: To już przechodzi moje pojęcie.
SALVIATI: Nie przejdzie, skoro tylko usunę wątpliwości, w jakich pan
jest pogrążony: gdvź zauważcie, że trzeba tu rozróżniać, czy ciężary są
w ruchu, czy też znajdują się w spoczynku. Kamień położony na wadze, nie
tylko stanie się cięższy, gdy doń dołączymy inny kamień, ale także gdy
dołożymy garść konopi, będzie ważył więcej o 6 lub 10 uncji, które waży
ta garść; ale jeżeli zrzucać będziecie kamień z wysokości, razem z
konopiami, to czy myślicie, że w ruchu konopie ciążyć będą na kamieniu i
mają przyspieszać jego ruch? albo że będą go podtrzymywać i jego ruch
opóźniać? Czy nie czujemy ciężaru na ramionach, gdy chcemy się opierać
jego ruchowi, ale jeżeli sami obniżamy się z taką samą prędkością, z
jaką by spadał ciężar, jakże chcecie, aby on tam naciskał lub ciążył?
Czy nie widzicie, że byłoby to tak, jakbyśmy chcieli uderzyć piką tego,
który biegnie przed nami z tą samą prędkością lub większą niż nasza.
Wyprowadźcie więc stąd wniosek, że przy swobodnym i naturalnym spadku
mały kamień nie ciąży na większy i nie powiększa jego ciężaru, jak wtedy
gdy są w spoczynku.
SIMPLICIO: Ale gdyby wielki kamień położony został na małym?
SALVIATI: To zwiększyłby jego ciężar, gdyby miał większą prędkość;
ale skoro doszliśmy już do wniosku, że, gdyby mały ciężar spadał
wolniej, to opóźniałby spadek większego, więc oba kamienie razem
spadałyby wolniej, co się sprzeciwia waszemu twierdzeniu. Dochodzimy więc do wniosku, że wielkie i małe ciała, tegoż samego ciężaru
gatunkowego, poruszają się z jednakową prędkością.
SIMPLICIO: Wywód wasz jest jak najprawdziwszy, a jednak trudno mi
jest uwierzyć, aby kropla ołowiu poruszała się równie prędko, jak kula
armatnia.
SALVIATI: Powiedzcie raczej ziarnko piasku jak kamień młyński. Nie
chciałbym, panie Simplicio, abyś tak czynił, jak inni i zbaczając od
kwestii głównej występował przeciwko mojemu poglądowi, różniącemu się
o włos od prawdy, i chciał tym włosem zakrywać czyjś inny błąd, gruby
jak lina okrętowa. Arystoteles mówi: stofuntowa kula żelazna, spadająca swobodnie z wysokości stu łokci,
wprzód dochodzi do ziemi, aniżeli jednofuntowa spadająca z wysokości
jednego łokcia; ja utrzymuję, że obie spadają równocześnie:
Wv
znajdujecie, że większa o dwa cale wyprzedza mniejszą, tak, że gdy
większa uderza o ziemię, to mała odległa jest od niej dwa cale; wy
chcecie temi dwoma calami zasłonić dziewięćdziesiąt dziewięć łokci
Arystotelesowych i, mówiąc tylko o moim małym błędzie, pomijacie
milczeniem drugi większy. Arystoteles mówi, że ciała różnego ciężaru w
tym samym ośrodku poruszają się (o ile to zależy od ciążenia) z
prędkościami proporcjonalnemi do ich ciężaru i daje jako przykład ciała,
których rozważać można tylko czysty absolutny ciężar, nie uwzględniając
wpływów, takich jak kształt, ich mniejsze momenty,
rzeczy na które silny wpływ wywiera ośrodek,
zmieniający proste działanie ciężkości, jak to widzimy przy złocie,
najcięższem gatunkowo ciele, które jako cienki arkusik unosi się w
powietrzu, a również pod postacią delikatnego proszku. Ale jeżeli
chcecie postawić ogólną zasadę, to trzeba, abyście wykazali stosunek
prędkości zaobserwowany przy wszystkich ciałach ciężkich i to, że kamień
dwudziestofuntowy dziesięć razy prędzej się porusza od dwufuntowego, co,
jak ja utrzymuję, jest równie błędne, gdyż spadając z wysokości
pięćdziesięciu lub stu łokci zawsze dojdą do ziemi w tej samej chwili.
SIMPLICIO: Ale może przy wielkiej wysokości tysiąca łokci
nastąpiłoby to, co się nie zdarza przy wysokości mniejszej.
SALVIATI: Gdyby Arystoteles przypuszczał coś podobnego,
obarczylibyście go innym błędem, któryby był kłamstwem; gdyż takich
pionowych wysokości na ziemi nie ma, więc rzecz jasna, że nie mógł
Arystoteles robić z nimi doświadczenia: a jednak chce on nas
przekonać, że je robił, bo powiada, że taki widać skutek.
SIMPLICIO: Zapewne Arystoteles nie posługiwał się tą zasadą, lecz
drugą, która nie sądzę, aby podlegała tej trudności.
SALVIATI: Ale ta druga jest niemniej mylna i dziwię się, że sami nie
zauważyliście pomyłki i nie spostrzegli, że gdyby była prawdziwą, to
według niej jedno i to samo ciało, w ośrodkach różnej gęstości, jak
np. w wodzie i powietrzu, poruszałoby się z prędkościami odwrotnie
proporcjonalnemi do gęstości, a więc wszystkie ciała, spadające w
powietrzu, musiałyby także spadać w wodzie; co jest zupełnie mylne, gdyż wiele ciał, które spadają w powietrzu, w
wodzie nie spada, ale unosi się do góry.
SIMPLICIO: Ja nie pojmuję potrzeby Waszego wniosku, a nadto dodam, że
Arystoteles mówi o takich ciałach, które w obu ośrodkach spadają, a nie o
takich, które spadają w powietrzu, a podnoszą się w wodzie.
SALVIATI: W obronie filozofa przytaczacie argumenty, których on nie
podałby z pewnością, aby pierwiastkowego swego błędu nie powiększać.
Powiedźcie mi przy tym, czy gęstość wody, albo to, co opóźnia jej bieg,
pozostaje w pewnym stosunku do gęstości powietrza, która mniej opóźnia
jego bieg, a jeżeli tak, to podajcie mi dowolną wartość tego stosunku.
SIMPLICIO: Zgoda, weźmy stosunek dziesięciokrotny; będzie się tym
sposobem ciało spadające w powietrzu poruszać dziesięć razy prędzej niż
w wodzie.
SALVIATI: Biorę teraz ciało, które spada w powietrzu a nie
spada w wodzie, jak np. kulę drewnianą i pytam się Was, jaką oznaczacie
prędkość jej spadku w powietrzu.
SIMPLICIO: Przyjmujemy, że będzie się poruszała z prędkością
dwudziestu stopni.
SALVIATI: Doskonale. Oczywiście może ta prędkość stoi do innej w tym
samym stosunku, jak gęstość wody do gęstości powietrza i ta inna
prędkość wynosić będzie tylko 2 stopnie, tak że w rzeczywistej zgodzie z
zasadą Arystotelesa wnioskować należy, że kula drewniana, która w
powietrzu spada z prędkością dwudziestu stopni, powinnaby spadać w
wodzie z prędkością 2 stopni, a nie podnosić się od dna i pływać na
powierzchni, jak to czyni; albo też chcieliście powiedzieć, że podnoszenie się w wodzie odbywa
się tak samo jak spadanie w powietrzu z prędkością dwóch stopni, czego
nie przypuszczam. Właśnie fakt, że kula nie spada na dno, pozwala mi
spodziewać się, że się zgodzicie na to, że można znaleźć inną kulę z
innego materiału, która by spadała w wodzie z prędkością dwóch stopni.
SIMPLICIO: Można, tylko materiał musi być znacznie cięższy od drewna.
SALVIATI: Tego właśnie szukam. Ale ta druga kula, która wwodzie spada
z prędkością dwóch stopni, jak prędko spadać będzie w powietrzu?
Powinnibyście odpowiedzieć (jeżeli chcecie posługiwać się zasadą
Arystotelesa), że z prędkością dwudziestu stopni; ale dwadzieścia stopni
prędkości przyznaliście sami kuli drewnianej; a więc tak ta, jak i druga cięższa, poruszałyby się w powietrzu z
jednakową prędkością. Jakże to pogodzi filozof z pierwszą swoją zasadą,
według której różne ciała, w jednym i tym samym ośrodku, poruszają się
z różnymi prędkościami, tak się różniącemi od siebie jak ich ciężkości.
Ale, nie bacząc już na to, jakże nie mogliście zaobserwować, jak dwa
ciała poruszają się w wodzie, jedno sto razy prędzej od drugiego,
podczas gdy, spadając w powietrzu, mają prędkości nie różniące się nawet
o jedną setną; albo jak jajko z marmuru spada w wodzie sto razy prędzej
od jajka kury, podczas gdy przy spadaniu obu jajek z wysokości
dwudziestu łokci w powietrzu, jajko marmurowe ani na cztery cale kurzego
nie wyprzedzi; że wreszcie niektóre ciała pogrążają się na głębokość
dziesięciu łokci w wodzie w ciągu
trzech godzin, podczas gdy na spadek w powietrzu potrzebują zaledwie
dwóch uderzeń pulsu, a inne (jakby to było z kulą ołowianą) czasu mniej
niż podwójnego. Tak tedy wiem dobrze, panie Simplicio, że mnie
rozumiecie, że nie ma różnicy zdań ani żadnej odpowiedzi. Wnosimy więc,
że ten argument nic nie przynosi przeciwko próżni, a gdyby nawet tak
było, to byłyby przez to usunięte tylko te wielkie próżnie, których ani
ja, ani, jak sądzę, starożytni nie przyjmowali jako dane od natury,
jakkolwiek mogą być robione siłą, jak to wynika z wielu dowodzeń, o
których zbyt długo byłoby tu mówić.
SAGREDO: Widząc że p. Simplicio milczy, pozwolę sobie podnieść
tu inną kwestię. Jakkolwiek dowiedliście jasno, że ciała nierównego
ciężaru w tym samym ośrodku nie poruszają się z prędkościami
proporcjonalnYmi do ich ciężkości, lecz z jednakowemi, przyjmując
przy tym, że ciała są z tegoż samego materiału albo
tegoż samego ciężaru gatunkowego, a nie (jak myślę) różnych ciężarów
gatunkowych (gdyż nie można wymagać, abyśmy wierzyli, że kula korkowa
porusza się równie prędko jak ołowiana) i dalej, że niesłuszne jest
twierdzenie, jakoby jedno i to samo ciało, w ośrodkach różnej
oporności, opóźniało lub przyspieszało swój ruch w stosunku odwrotnym do
oporności; pragnąłbym więc bardzo dowiedzieć się, jaki stosunek
zaobserwowany został w jednym i drugim przypadku.
SALVIATI: Zadania są piękne i wiele nad nimi rozmyślałem.
Wyłożę wam
mój pogląd, choć jeszcze nie w ostatecznej formie. Po przekonaniu się o
nieprawdziwości tego, że jedno i to samo ciało, w różnych ośrodkach,
osiąga prędkości odwrotnie proporcjonalne do oporów, jak i tego, że
ciała różnego ciężaru, w jednym i tym samym ośrodku, osiągają prędkości
proporcjonalne do swych ciężarów (nawet przy samej różnicy ciężarów
gatunkowych), skombinowawszy oba te zjawiska przez umieszczenie różnych
ciał w różnych ośrodkach, znalazłem, że osiągnięte prędkości tym więcej
się różnią, im opór ośrodka jest większy i to w tym stosunku, że dwa
ciała, które w powietrzu spadają z bardzo mało różniącymi się
prędkościami, w wodzie mogą mieć prędkości dziesięć razy większe
jedna od drugiej; zdarza się także, że ciało spada w powietrzu, a w
wodzie pływa tj. wcale nie spada, a nawet się podnosi: toteż można
znaleźć takie gatunki drzewa, albo sękate ich części, albo korzenie,
które pozostają zawieszone w wodzie, podczas gdy spadają szybko w
powietrzu.
SAGREDO: Usiłowałem nieraz bardzo cierpliwie kulkę wosku, która sama
w wodzie się nie zanurza, oblepiać ziarnkami piasku, dopókąd nie
nabierze ciężaru równego wodzie i nie stanie w jej wnętrzu; pomimo całej
ostrożności nie udało mi się tego dokonać. Nie wiem, czy jest inne jakieś
ciało, które by miało gęstość równą wodzie, tak aby mogło pozostawać w
niej w tym samem miejscu, w jakiem je ustawiono.
SALVIATI: Tak do tej, jak i do tysiąca innych czynności więcej jest
od nas uzdolnionych wiele zwierząt. W waszym przypadku, dostarczyć mogą
pewnego dowodu ryby, będące do tej czynności tak usposobione, że dowoli
utrzymują się w równowadze, nie tylko w czystej wodzie, ale i w różnych
jej rodzajach natrafianych w naturze, jak zanieczyszczonej czy to
szlamem, czy solą, choćby różnica gęstości była znaczna; i utrzymują
się w równowadze tak ściśle, że bez poruszania pozostają w spokoju w
każdem miejscu; czynią to, posługując się danem im przez naturę
narzędziem, małym pęcherzykiem wewnątrz ciała, który przez ważki
kanalik komunikuje się z wnętrzem paszczy, tak że stosownie do potrzeby
znajdujące się w pęcherzyku powietrze zostaje wypchnięte, albo gdy ryby
są na powierzchni wody, wciągnięte zostaje nowe powietrze i przez tę
sztukę stają się to cięższymi, to lżejszymi od wody i w każdym miejscu
mogą się utrzymać w równowadze.
SAGREDO: Ja znów inną sztuką zwodziłem moich przyjaciół, przed
którymi się chwaliłem, że doprowadzam wosk do ścisłej równowagi z wodą.
Nalawszy na spód naczynia wodę słoną, dolałem słodkiej i wtedy wosk
utrzymywał się stale pośrodku naczynia, opadał do środka, gdy był
podnoszony, a podnosił się, gdy był popchnięty do dna.
SALVIATI: Nie bez użytku jest takie doświadczenie: gdy lekarze
badają własności różnych wód, a między innymi głównie lekkość lub
ciężkość, większą jednych niż drugich, to urządzają taką kulkę, aby
wykazywała jak najmniejsze różnice, pogłębiając się w jednej wodzie, a
podnosząc w drugiej. I w ten sposób tak dokładne jest doświadczenie, że
przez dodanie tylko dwóch granów soli do sześciu funtów wody, kulka
leżąca na dnie podnosi się do samej góry, skąd przedtem opadła. Na dowód
dokładności tego doświadczenia, oraz braku wszelkiego oporu przy
rozdzielaniu cząstek wody, dodać mogę, że nie tylko powiększenie jej
ciężaru przez domieszanie cięższej substancji, taki sprawia skutek, ale
także proste rozgrzanie i ochłodzenie i to z taką czułością, że przez
wprowadzenie czterech kropli innej wody nieco chłodniejszej lub
cieplejszej, do tych sześciu funtów, wywołuje się opadanie lub
podnoszenie kulki, która przy dodaniu zimnej wody podnosi się, a ciepłej
- opada. Widzicie teraz, jak się mylili ci filozofowie, którzy
przyznawali wodzie lepkość albo inne związanie cząstek, stawiające opór
rozdzielaniu i przenikaniu.
SAGREDO: Znalazłem wiele przekonywających rozważań w tym
przedmiocie w jednej rozprawie naszego akademika, ale mimo to pozostaje
mi wielka wątpliwość, której nie mogę usunąć: jeżeli nie ma żadnej
lepkości lub spójności między cząstkami wody, jakże się mogą utrzymywać
duże krople, często spostrzegane zwłaszcza na liściach kapusty, bez
spłaszczania się i rozlewania?
SALVIATI: Jakkolwiek każdy, kto uważa swój pogląd za słuszny, winien
odpierać wszelkie zarzuty, tu jednak nie mogę przyznawać sobie możności
zrobienia tego, ale moja nieudolność nie powinna zamącać jasności
prawdy. Przyznaję się najpierw, że nie wiem, w jaki sposób utrzymują się
wysokie i wielkie krople, jakkolwiek wiem na pewno, że to nie pochodzi
ze spójności wewnętrznej cząstek i że przyczyny zjawiska szukać należy
na zewnątrz. Że ona nie jest wewnętrzna, mogę Was o tym, oprócz
poprzedniego doświadczenia, przekonać innym, nader dowodnem. Gdyby
cząstki tej wody, która utrzymuje się podniesiona, podczas gdy jest
otoczona powietrzem, miały wewnętrzną przyczynę trzymania się razem, to
ta pewniej jeszcze miałaby miejsce, gdyby się znajdowały w otoczeniu, w
którym miałyby mniej dążności do opadania na dół, niż w powietrzu; ale
takim ośrodkiem może być każdy płyn cięższy od powietrza, np. wino,
tylko że otoczenia kropli wody winem nie da się zrobić bez rozpuszczenia
cząstek wody, trzymających się razem swą wewnętrzną lepkością; ale
rozpuszczenie to nie następuje wcześniej, aż obca ciecz zostanie
zbliżona, przy czym woda zaraz się rozchodzi, nie czekając rozpuszczenia
lub zmieszania, jak to ma miejsce z winem czerwonym; a więc przyczyna
zjawiska jest zewnętrzna i może pochodzić od powietrza, l rzeczywiście,
zauważyć można wielką niezgodność między powietrzem a wodą, jak to
zaobserwowałem przy następującym doświadczeniu. Jeżeli bańkę szklaną,
mającą otwór mały jak słomka, napełnię wodą i jeżeli tak napełnioną
bańkę odwrócę otworem do spodu, to woda nie wypłynie, jakkolwiek jest
cięższą, a powietrze chociaż lżejsze nie wchodzi do bańki, zwykle tak
jedno, jak i drugie pozostają w spokoju. Jeżeli zaś tak odwróconą bańkę
zanurzę otworem w czerwonem winie, które zaledwie trochę jest lżejsze
od wody, to widzimy zaraz, jak czerwone promienie wchodzą do bańki, woda
opuszcza się do wina, jakkolwiek się ze sobą nie mieszają, aż w końcu
wino wypełni bańkę, a woda zejdzie do spodu naczynia z winem. Cóż mamy o
tym powiedzieć i czym to wytłumaczyć, jeżeli nie niezgodą między wodą a
powietrzem, nieznaną mi, którą może...
SIMPLICIO: Śmiać się muszę z antypatii pana Salviati'ego, do wyrazu
antypatia, którego on nie chce tu wymówić, a który tak się nadaje do
przecięcia trudności.
SALVIATI: Niechże takie będzie, dzięki panu Simplicio, rozwiązanie
naszej wątpliwości i wróćmy po tym zboczeniu do naszego zadania.
Widzieliśmy, że różnica prędkości spadania różnych ciał jest znacznie
większa w ośrodkach więcej opornych: ale złoto nie tylko spada w
rtęci prędzej niż ołów, jest nadto jedynym metalem, który w nim
spada, bo inne metale podnoszą się i pływają; z drugiej strony, kulki
ze złota, ołowiu, miedzi, porfiru i innych ciał ciężkich spadają w
powietrzu z prędkościami, których różnice nie dają się zauważyć i pewno
kulka złota, w końcu swego spadku z
wysokości stu łokci nie wyprzedzi kulki miedzianej nawet o cztery cale;
z uwagi na to, jestem zdania, że gdyby usunąć zupełnie opór ośrodka, to
wszystkie ciała spadałyby z jednakową prędkością.
SIMPLICIO: Śmiałe to twierdzenie, panie Salviati. Co do mnie, nigdy
nie uwierzę, aby w jednej i tej samej próżni, gdy się ruch odbywa,
pęczek wełny spadał równie prędko jak kawał ołowiu.
SALVIATI: Ostrożnie, panie Simplicio. Pogląd pański nie jest tak
uzasadniony, ani ja nie jestem tak nieopatrzny, aby można było sądzić,
że nie mam lub nie mogę znaleźć wytłumaczenia. Posłuchajcie więc, co
powiem dla mego usprawiedliwienia i przekonania was.
Badać mamy ruch
różnych ciał w ośrodku nie stawiającym oporu, tak że wszelkie różnice
prędkości ciał spadających zostaną usunięte. A ponieważ jedynie tylko
przestrzeń, w której zupełnie nie ma powietrza ani żadnej materii choćby
najrzadszej i najmniej opornej, mogłaby wykazać to, czego szukamy i
ponieważ takiej przestrzeni nie możemy wytworzyć, to spróbujmy
zobaczyć, co się dzieje w ośrodkach najrzadszych i najmniej opornych, w
porównaniu z innymi. Znajdujemy istotnie, że różne ciała różnią się tym
mniej w swym ruchu, im ośrodki są mniej oporne i że w rezultacie,
pomimo wielkiej różności ciał spadających w najrzadszym ośrodku,
zauważyć można różnice prędkości ledwie dostrzegalne, zaledwie
istniejące; dlatego wydaje mi się, że możemy przyjmować z wielkim
prawdopodobieństwem, iż w próżni nie będzie wcale tych różnic. Bo
zważmy, co się dzieje w powietrzu; ażeby zaś mieć ciało ściśle
oznaczonego kształtu, z bardzo lekkiej materii, weźmy wydęty pęcherzyk,
pełen powietrza, które zważone w powietrzu nic nie waży (albo bardzo
mało, bo mogło być nieco ściśnięte w pęcherzyku), tak że ciężar całego
pęcherzyka składa się tylko z ciężaru powłoki, a więc nie wynosi ani
tysiącznej części ciężaru tej samej wielkości kulki ołowianej. Takie
dwa ciała, panie Simplicio, spuśćcie z wysokości czterech do pięciu
łokci; o ile, myślicie, że ołów spadnie wcześniej od pęcherzyka?
Bądźcie pewni, że ani dwa ani trzy razy prędzej, chociaż uczyniliście go
tysiąckrotnie prędszym.
SIMPLICIO: Być może, że w początku ruchu, w ciągu pierwszych
czterech do sześciu łokci, będzie tak jak mówicie, ale w dalszym ciągu,
przy dłuższem spadaniu, sądzę, że ołów pozostawi po za sobą pęcherzyk
nie tylko na 1/12 część
przestrzeni, ale na sześć, osiem i dziesięć.
SALVIATI: I ja tak myślę i nie wątpię, że przy bardzo wielkich
wysokościach, ołów może spadać sto mil, podczas gdy pęcherzyk tylko
jedną milę. Ale, mój panie Simplicio, właśnie to, co przedstawiacie
jako zjawisko przeczące memu poglądowi, najwięcej ten pogląd potwierdza.
Wykazuje ono, że przyczyną różnic prędkości ciał różnego ciężaru nie
może być ten ciężar, lecz że ta przyczyna zależy od okoliczności
zewnętrznych, a zwłaszcza od oporu ośrodka, tak że po usunięciu tego
oporu wszystkie ciała poruszają się z tymi samymi stopniami prędkości.
Wywodzę to głównie z poglądu, co dopiero przez was przyjętego, który
jest zupełnie słuszny, że ciała różnego ciężaru tym więcej się różnią
co do prędkości, z jakimi spadają, im większe przebywają odległości:
co nie miałoby miejsca gdyby przyczyną była różność ciężarów. Bo
ponieważ te ciężary są wciąż te same, to również ten sam stosunek
winien się utrzymywać między przebytymi przestrzeniami, który to
stosunek widzimy, że stale wzrasta podczas ruchu; bo bardzo ciężkie
ciało nie wyprzedzi o 1/12 część przebytej
przestrzeni bardzo lekkiego przy spadku z wysokości jednego łokcia, z
wysokości 12 łokci wyprzedzi o 1/3, a ze
100 łokci o 90/100.
SIMPLICIO: Bardzo dobrze, ale jeżeli według Was różnica ciężaru, przy
ciałach różnej ciężkości gatunkowej, nie wywołuje proporcjonalnych
zmian prędkości, to znów gdy ciężary są jednakowe, wtedy ośrodek,
pozostając wciąż ten sam, nie powinien powodować zmiany prędkości.
SALVIATI: Podnieśliście przeciw mojemu poglądowi ciężki zarzut,
który koniecznie muszę odeprzeć. Powiedziałem co dopiero, że
ciało
ciężkie posiada w sobie daną przez naturę własność poruszania się w
kierunku wspólnego środka ciał ciężkich tj. ku naszej kuli ziemskiej i
to ruchem stale i zawsze jednostajnie przyspieszonym, tak że w czasach
równych dochodzą nowe momenty i stopnie prędkości. I to zawsze może być
sprawdzone, jak tylko usunięte zostaną przypadkowe przeszkody
zewnętrzne; między nimi jest jedna, która się nie daje usunąć,
mianowicie ośrodek, który musi się otwierać przed ciałem spadającym i
usuwać na bok, a temu swemu ruchowi bocznemu ośrodek, nawet gdy jest
płynny, ustępliwy i spokojny, zawsze stawia opór, który stosownie do
okoliczności jest większy lub mniejszy, a zwłaszcza tym większy im
prędzej ośrodek musi się otwierać dla przepuszczenia ciała, które przez
to, z natury spadając ruchem przyspieszonym, doznaje wciąż rosnącego
oporu; powstaje stąd opóźnienie i zmniejszenie nowo nabytych prędkości,
tak że te w końcu, podobnie jak doznawane opory, dochodzą do tego
stopnia, że się równoważą i znoszą wszelkie przyspieszenie, a ciało
wprowadzają w ruch jednostajny, w którym ono dalej pozostaje. Więc
powiększenie oporu w ośrodkach nie polega na żadnej zmianie ich istoty,
ale na prędkości, z jaką ośrodek musi się otwierać i w bok usuwać, aby
ciału spadającemu z przyspieszeniem dać przejście. Teraz, widząc, że
opór, jaki stawia powietrze małemu momentowi spadającego pęcherzyka jest
bardzo wielki, przeciwnie zaś wielkiemu ciężarowi ołowiu bardzo mały,
dochodzę do wniosku, że, gdyby można było opór ten zupełnie usunąć i dać
przez to pęcherzykowi jak największą wygodę a bardzo małą ciężarowi
ołowianemu, to zrównałyby się ich prędkości. Stawiam przeto zasadę, że
w przestrzeni próżnej albo skądinąd nie stawiającej żadnej przeszkody
prędkościom ruchu, tak że wszystkie ciała poruszać się w niej będą z
jednakową prędkością, będziemy mogli poznać dość dokładnie stosunki
prędkości ciał podobnych i niepodobnych, poruszających się w tym samym
ośrodku i w różnych ośrodkach zapełnionych, a przez to opornych.
Dojdziemy do tego, biorąc pod uwagę, ile ciężar ośrodka ujmuje
ciężarowi poruszającego się ciała, gdyż przewyżka ciężaru jest środkiem
pomocniczym, za pomocą którego ciało przebija sobie drogę, odsuwając na
boki części ośrodka, okoliczność, która nie zachodzi w próżni i dlatego
nie ma tam różnicy, jakiej oczekiwać można z różności ciężaru
gatunkowego. A ponieważ okazuje się stąd, że ośrodek odciąga tyle
ciężkości poruszającemu się w nim ciału, ile waży wypchnięta część
ośrodka, więc, zmniejszając w tej proporcji prędkość spadającego ciała,
która byłaby równą w ośrodku nie
opornym (jak to przypuszczono), otrzymamy to, czego szukamy. Przyjmując
np. że ołów jest 10000 razy cięższy od powietrza, a heban tylko 1000
razy, to od prędkości obu tych ciał, które w ośrodku bez oporu byłyby
równe, odejmie powietrze od ołowiu z 10000 stopni jeden, a od hebanu z
1000 stopni jeden, co znaczy z 10000 dziesięć. Gdy więc ołów i heban
spadają w powietrzu z jakiejkolwiek wysokości, którą, gdyby opór
powietrza był usunięty, przebyłyby w tym samym czasie, to powietrze
odejmie od prędkości ołowiu z 10000 stopni jeden a od hebanu z 10000
dziesięć, co znaczy, że podzieliwszy wysokość spadku na 10000 części,
ołów spadnie, gdy heban będzie za nim 10 mniej jeden czyli dziewięć
części w tyle. A cóż jest innego, jeżeli znajdujemy, że spuszczając z
wieży 200 łokciowej kulkę ołowianą to ona wyprzedza hebanową o 4 cale ?
Heban waży 1000 razy więcej od powietrza, ale ten pęcherzyk, który był
wydęty waży tylko cztery razy tyle; powietrze więc odciągnie od
naturalnej prędkości hebanu z tysiąca stopni jeden, a od tej, która by
dla pęcherzyka była absolutnie taką samą, powietrze nie odciągnie jak
tylko z czterech części jedną. Gdy zatem kulka hebanu dosięgnie ziemi,
pęcherzyk przeleci tylko 3/4 wysokości. Ołów jest dwanaście razy cięższy
od wody, a kość słoniowa tylko dwa razy: woda więc od ich absolutnych
prędkości, które byłyby równe, odciągnie dla ołowiu 1/12,
a dla kości słoniowej 1/2: w wodzie więc, gdy
ołów zejdzie jedenaście łokci, kość słoniowa zejdzie tylko na sześć.
Rozumując według tej zasady, sądzę, że znajdziemy, iż doświadczenie
ściślej odpowiada takiemu rachunkowi niż Arystotelesowemu. W podobny
sposób znaleźć można stosunek między prędkościami tegoż samego ciała w
różnych ośrodkach płynnych, nie przez porównywanie różnych oporów tych
ośrodków, ale przez rozważanie przewyźek ciężkości ciała nad ciężkością
ośrodków; cyna jest np. 1000 razy cięższa od powietrza, a 10 razy od
wody, więc jeżeli podzielimy prędkość absolutną cyny na 1000 stopni, to
w powietrzu, które z niej nie ujmuje 1/1000 części, poruszać się będzie z
prędkością 999 stopni, a w wodzie tylko z prędkością 900 stopni,
ponieważ woda ujmuje 1/10 część jej ciężkości a
powietrze 1/1000. Niech będzie ciało nieco cięższe od wody np. drzewo dębowe i
niech waży kula z niego 1000 drachm, a takaż kula wody 950, zaś
powietrza 2, to oczywiście, przyjmując, że absolutna jej prędkość jest
1000 stopni, to w powietrzu byłaby 998, a w wodzie tylko 50 stopni, bo
woda z jej 1000 stopni ciężkości zostawia tylko 50; ciało to
więc poruszałoby się w powietrzu 20 razy prędzej niż w wodzie, gdyż
przewyżka jego ciężkości nad ciężkością wody jest tylko dwudziestą
częścią jego własnej. I co chciałbym jeszcze zauważyć, że opadanie w
wodzie możliwe jest wtedy tylko, gdy ciężar gatunkowy ciała jest większy
niż wody; a to są ciała wieleset razy cięższe od powietrza; dla
znalezienia więc proporcji prędkości ich w wodzie i w powietrzu możemy
bez znaczniejszego błędu rachować, że powietrze nic nie odejmuje
momentowi absolutnej ciężkości, a więc i absolutnej prędkości tych
ciał; znalazłszy więc łatwo przewyżkę ciężkości ciała nad ciężkością
wody, powiemy, że jego prędkości w powietrzu i w wodzie mają się do
siebie jak jego prędkość absolutna do przewyżki nad ciężkością wody. Np.
kula z kości słoniowej waży 20 uncji, takaż sama z wody 17, a więc
prędkość kuli w powietrzu i w wodzie mają się do siebie w przybliżonym
stosunku 20 do 3.
SAGREDO: Wielki nabytek zrobiłem w jednej, samej przez się
interesującej, kwestii, nad którą często, niestety bezskutecznie
rozmyślałem; nic by już nie brakło do zużytkowania tych wywodów, jak
tylko znalezienie sposobu oznaczania ciężkości powietrza w porównaniu z
wodą, a więc i z innymi ciałami ważkimi.
SIMPLICIO: Ale gdyby znaleziono, że powietrze posiada nie ciężkość,
ale lekkość, to cóż stąd wyniknie dla całego rozważania, skądinąd bardzo
dowcipnego?
SALVIATI: Wypadałoby powiedzieć, że było powietrze lekkie i puste.
Ale czyżbyście chcieli wątpić o ciężkości powietrza, choć macie jasny
tekst Arystotelesa, utrzymujący, że wszystkie elementy mają ciężkość, a
tak samo i powietrze? Czego dowodem (jak on dodaje) jest, że sakwa
nadęta waży więcej niż wypróżniona.
SIMPLICIO: Że sakwa lub bania nadęta waży więcej, mniemałbym, że to
pochodzi nie z ciężkości powietrza, ale z wielu, w niższych naszych
okolicach domieszanych gęstych wyziewów, przy pomocy których ciężar
sakwy wzrasta.
SALVIATI: Nie podoba mi się to, co mówicie, a mniej jeszcze, że
powołujecie się na Arystotelesa, bo on, mówiąc o elementach i chcąc
dowieść, że element powietrza ma ciężkość, uwidoczniłby to
doświadczeniem; gdyby mi w swem dowodzeniu powiedział: biorę sakwę,
napełniam ją gęstymi wyziewami i obserwuję przyrost ciężaru,
odpowiedziałbym mu, że ważyłaby jeszcze więcej, gdyby była napełniona
otrębami; ale dodałbym zaraz, że takie doświadczenia dowodzą tylko, że
otręby i gęste wyziewy są ciałami ciężkimi, co do powietrza wszakże
pozostaje taka sama wątpliwość jak i przedtem. Wszakże doświadczenie
Arystotelesa jest dobre i zasada prawdziwa. Inaczej za to rzecz się ma z
nauką innego filozofa, którego nazwiska nie pomnę, ale wiem, że ją
czytałem, który dowodził, że powietrze jest raczej ciężkie niż lekkie,
gdyż łatwiej ciężkie ciała niesie na dół niż lekkie do góry.
SAGREDO: Wybornie, doprawdy. Byłoby na mocy tego powietrze
wiele cięższe od wody, jakkolwiek wszystkie ciała ciężkie spadają
łatwiej w powietrzu niż w wodzie, a wszystkie lekkie łatwiej w wodzie
niż w powietrzu, przeciwnie niezliczone ciała podnoszą się w wodzie a
spadają w powietrzu. Ale, panie Simplicio, czy ciężkość sakwy pochodzi
od ciężkich wyziewów czy od czystego powietrza, to się nic nie
sprzeciwia naszej zasadzie, gdyż my badamy, jak się ciała poruszają w
tej przestrzeni gazowej. Toteż wracając do tego, co mnie więcej
zajmuje, chciałbym dla gruntownego i absolutnego zbadania tej kwestii
nie tylko być zapewnionym, że powietrze jest ciężkie (gdyż uważam to za
przesądzone), ale także dowiedzieć. się, jaka jest jego ciężkość.
Przeto proszę pana Salviati o udzielenie nam o tym wiadomości, jakie
posiada.
SALVIATI: Że powietrze ma ciężkość pozytywną, a nie, jak to myśleli
niektórzy, lekkość, której nie ma w żadnej materii,
tego dostatecznie
dowodzi doświadczenie Arystotelesa z wydętym balonem, gdyby bowiem dany
był powietrzu przymiot lekkości, to przy powiększaniu ściskania
powietrza wzrastałaby lekkość a więc i popęd wznoszenia się do góry, a
doświadczenie daje wynik przeciwny. Co do drugiej kwestii, jakim
sposobem badać można ciężkość powietrza, to używałem następującej
metody. Wziąłem dość dużą flaszkę szklaną, z wąską szyjką, którą
nakryłem naparstkiem ze skóry, przylegającym mocno do zwężenia szyjki i
mającym na wierzchu wstawioną i ściśle umocowaną błonkę, przez którą, za
pomocą szprycki wtłaczałem z siłą do flaszki wielką ilość powietrza,
które tak zostało zgęszczone, że można by było napełnić nim dwie do
trzech innych flaszek, oprócz tego, które się w niej naturalnie
znajdowało. Potem, na bardzo dokładnej wadze, zważyłem ściśle flaszkę
wraz ze zgęszczonem w niej powietrzem, wyrównując wagę odrobiną
piasku. Po otwarciu błonki i gwałtownern wyjściu ściśnionego powietrza,
flaszka ponownie postawiona na wadze okazała się znacznie lżejszą i
trzeba było dla jej zrównoważenia odjąć część piasku. Niewątpliwie
ciężar tej części piasku był ściśle równy ciężarowi powietrza, które
było w niej ściśnięte i w końcu wypuszczone. Doświadczenie to wykazało
tylko, jaki był ciężar wypuszczonego z flaszki powietrza, równy
ciężarowi odjętego piasku; ale ile ostatecznie i ściśle waży powietrze w porównaniu
z wodą lub innymi ciałami ciężkimi, tego się nie dowiedziałem i nie
mogłem wiedzieć, dopóki nie zmierzyłem ilości wypuszczonego powietrza.
Aby tego dokonać, można postępować w dwojaki sposób. Pierwszy polega na
wzięciu drugiej podobnej flaszki z szyjką, która także zaopatrzona jest
w naparstek skórzany, ale otwarty i taki, że może obejmować naparstek z
błonką pierwszej flaszki, do którego ściśle jest przywiązany. Ta druga
flaszka ma otwór w dnie, przez który można wsuwać pręcik żelazny i z
jego pomocą dziurawić błonkę i umożliwiać przejście zgęszczonego
powietrza z pierwszej flaszki do drugiej, pełnej wody. Gdy wszystko
przygotowane i błonka prętem przebita, powietrze wpada do flaszki
napełnionej wodą i wypycha wodę przez otwór na zewnątrz; oczywiście tak
otrzymana ilość wody równa będzie objętości powietrza, które wyszło z
pierwszej flaszki. Zatrzymuje się tę wodę i waży flaszkę, z której
wyszło powietrze (którą przypuszczam zważono przedtem z powietrzem
ścieśnionym), odejmując, jak powiedziano, część piasku, która
oczywiście wyraża ciężar tej objętości powietrza, jaka jest objętość
wody, wypchniętej i wyciekłej; tę wodę ważymy i otrzymujemy, ile razy
jej ciężar jest większy od ciężaru odjętego piasku; i bez błędu możemy
orzec, ile razy cięższa jest woda od powietrza i to nie będzie dziesięć
razy, jak oceniał Arystoteles, ale około czterystu, jak to wykazało
doświadczenie.
Drugi sposób jest szybszy i może być przeprowadzony z jednem
naczyniem, którem jest flaszka przygotowana, jak była mowa, z
powietrzem, jakie się w niej naturalnie znajduje, bez wstrzykiwania
nowego z zewnątrz; do tej flaszki wtłacza się wodę, nie wypuszczając
powietrza, tak że się ono w niej zgęszcza. Po wprowadzeniu wody, ile
tylko można, co wynosi około 3/4 objętości
flaszki, ważymy flaszkę jak najdokładniej, a następnie odwracamy szyjką
do góry i przebijamy błonkę; wychodzi wtedy z flaszki taka objętość
powietrza, ile miejsca zajmuje pozostała we flaszce woda; po czym ważymy
znów flaszkę i otrzymujemy, ile jej ubyło ciężaru przez wyjście
powietrza; będzie to ciężar tej objętości powietrza, którą woda
wypchnęła z flaszki.
SIMPLICIO: Nie mogę powiedzieć, aby obmyślone przez Was sposoby nie
były eleganckie i dowcipne, zdaje mi się wszakże, że o ile na pozór są
zadowalające, to znów z innej strony wywołują powątpiewanie. Mianowicie,
w swojej własnej dziedzinie elementy niewątpliwie nie są ani ciężkie ani
lekkie, toteż nie mogę pojąć, jak ta ilość powietrza, która niewiele
co ważyła, dajmy na to cztery drachmy piasku, mogła jednak mieć tę
ciężkość w powietrzu, w którym piasek ją równoważył: mnie się zdaje, że
doświadczenie nie powinno było odbywać się w powietrzu, ale w innym
ośrodku, w którym powietrze wykazywać by mogło swoją zdolność ciążenia,
jeżeli takową posiada.
SALVIATI: Zarzut pana Simplicio jest ciężki i, albo nie ma nań
odpowiedzi, albo też odpowiedź winna być nie mniej subtelna. Że to
powietrze, które zostało zgęszczone i dało się zważyć odjęciem piasku,
skoro wróciło do swego elementu, nie było już możliwe do zważenia, to
prawda; zważyć można było tylko piasek; toteż dla wykonania takiego
doświadczenia powinno by być wybrane takie miejsce, w którym i powietrze
i piasek mogłyby ciążyć; bo, jak już była mowa, ośrodek odciąga od
każdego z zanurzonych w nim ciał tyle
z ich ciężaru, ile waży wypchnięta przez nie część ośrodka, tak że
powietrze od powietrza odciąga cały ciężar; gdybyśmy chcieli postępować
ściśle, musielibyśmy ważyć w próżni, gdzie każde ciało wywiera swój
moment, bez żadnego zmniejszenia. Gdybyśmy więc mogli, panie Simplicio,
zważyć pewną ilość powietrza w próżni, to czy byłbyś pan wtedy
objaśniony i upewniony?
SIMPLICIO: Tak istotnie, ale to jest życzenie lub wymaganie
niemożliwości.
SALVIATI: Będziecie mi więc obowiązani, gdy stosownie do życzenia
uskutecznię Wam tę niemożliwość, inaczej nie mógłbym Wam sprzedać
tego, co przed chwilą Wam dałem, bo w opisanym doświadczeniu ważyliśmy
powietrze w próżni, a nie w powietrzu lub innym wypełnionym ośrodku. Że
każde ciało, panie Simplicio, zanurzone w ośrodku płynnym, doznaje
ubytku ciężaru, pochodzi to stąd, że ośrodek opiera się rozwarciu,
wyparciu i podniesieniu; oznaką tego jest pośpiech, z jakim ośrodek wypełnia przestrzeń, którą
jakie wielkie ciało przedtem w nim zajmowało; gdyby ośrodek nie
odczuwał zanurzenia, nie oddziaływałby przeciw niemu. Powiedźcie mi więc,
jeżeli macie w powietrzu flaszkę omawianą, napełnioną powietrzem
naturalnym, jakiż to rozdział, parcie i w ogóle jaką zmianę zrobiło w
powietrzu zewnętrznym to powietrze, które zostało gwałtownie wtłoczone
do flaszki. Czyż powiększyła się flaszka, żeby powietrze otaczające
musiało odstępować dla zrobienia miejsca? Oczywiście nie: możemy więc
powiedzieć, że powietrze ściśnięte nie jest zanurzone w otaczającym, bo
ono żadnej w nim przestrzeni nie zajmuje, a jest jakby umieszczone w
próżni; i rzeczywiście znajduje się ono w próżni, zmieszane z niezupełnie tę
próżnię wypełniającem powietrzem naturalnym.
W istocie nie ma żadnej różnicy między dwoma przypadkami otaczającego
ośrodka, gdyż w jednym nie wywiera ten ośrodek żadnego ciśnienia na to,
co jest otoczone, a w drugim znów to, co jest otoczone, nie działa
zupełnie na ośrodek otaczający; i umieszczenie ciala w próżni jest tym
samym co ściśnięcie powietrza we flaszce. Znaleziony więc ciężar
ściśniętego powietrza jest ten sam, jaki by miało to powietrze po
rozejściu się w próżni. Zapewne, że w próżni ważyłby piasek nieco
więcej, ale dodać trzeba, że powietrze ściśnięte nieco więcej ważyło niż
piasek, lecz tylko tyle więcej, ile ważyłaby w próżni wypchnięta przez
piasek mała ilość powietrza.
SIMPLICIO: Zdawało mi się, że te doświadczenia zostawiały coś do
życzenia; ale obecnie jestem zupełnie zaspokojony.
SALVIATI: Kwestie, jakie roztrząsałem, a właszcza ta, że różnica
ciężkości, choćby największa, nie ma żadnego udziału w różnicy prędkości
spadku, tak że raczej wszystkie ciała poruszają się spadając z
jednakową prędkością, kwestia ta jest zupełnie nową, na pierwszy rzut
oka nieprawdopodobną, tak że, gdyby nie można jej było dostatecznie
rozświetlić i przedstawić jaśniejszą od słońca, byłoby lepiej o niej
zamilczeć niż mówić; skoro jednak już mi z ust wyszła, to nie mogę
pominąć doświadczenia czy dowodu, który może się przyczynić do jej
rozwiązania.
SAGREDO: Nie tylko to, ale także wiele innych Waszych podań są
tak dalekie od poglądów i nauk ogólnie przyjętych, że rozpowszechnione
publicznie wzbudzą znaczną liczbę oponentów, gdyż wrodzoną właściwością
człowieka jest: choć się ma dobre oczy, nie widzieć tego, co odkrywa
inny, przez swą wprawę w odróżnianiu prawdy od fałszu; niemiłą dla wielu
uszu nazwą nowatorów w nauce starają się rozcinać węzły, których sami
nie mogą rozwiązać, burząc podziemnYmi minami budowle, przez cierpliwych
mistrzów wzniesione: dalecy od tych niedorzeczności przyjmujemy Wasze
doświadczenia i wywody bez niepokoju; ale jeżeli macie jeszcze więcej
dotykalne doświadczenia i skuteczniejsze wywody, wysłuchamy ich bardzo
chętnie.
SALVIATI: Doświadczenie z dwoma ciałami, jak najwięcej różnego
ciężaru, które spadają z wysokości, dla obserwowania, czy ich prędkości
są równe, przedstawia pewną trudność, bo przy większej wysokości
ośrodek, który pod impetem spadającego ciała wciąż się rozwiera i
odrzucany jest na boki, ma większy wpływ na mały moment bardzo lekkiego
ciała, niż na gwałtowność bardzo ciężkiego, gdyż przy długiej
przestrzeni lekkie ciało zostawać będzie w tyle, a przy malej wysokości
wątpić można, czy jest jaka różnica, gdyż zaledwie można ją dostrzec.
Dlatego rozważałem, czy nie można by powtarzać spadku wielokrotnie na
niewielkich wysokościach i gromadzić razem tylu ile można małych różnic
czasu przybycia do kresu ciała ciężkiego i ciała lekkiego, które razem
dałyby czas nie tylko możliwy, ale nawet bardzo się nadający do
zaobserwowania. Z drugiej strony, dla możliwości badania jak
najpowolniejszych ruchów, przy których dla braku pracy oporu ośrodka,
zmieniającej działanie zależne od samej ciężkości, umyśliłem spuszczać
ciała wzdłuż słabo nachylonej płaszczyzny, bo i przy takim spadku, tak
samo jak i przy swobodnym, można dostrzec, jak się poruszają ciała
różnego ciężaru; idąc dalej, chciałem się jeszcze oswobodzić od
przeszkód, powstających przy zetknięciu ciała z płaszczyzną nachyloną:
w końcu wziąłem dwie kulki, jedną z olowiu a drugą z korka, jedną sto
razy cięższą od drugiej i zawiesiłem obie na dwóch cienkich sznurkach
jednakowej długości, od czterech do pięciu łokci; odchylając obie kulki
od ich zawieszenia pionowego, puszczałem je swobodnie i one spadały po
okręgach kół jednakowego promienia, przekraczały położenia pionowe
sznurków i tą samą drogą wracały, a po stu wahaniach w jedną i drugą
stronę okazało się wyraźnie, że ciało ciężkie poruszało się tak
równocześnie z lekkiem, że ani w stu
ani tysiącu wahań nie dała się zauważyć jak najmniejsza różnica;
chodziły zupełnie równym krokiem, zauważyć się też dawał wpływ ośrodka,
stawiający pewien opór ruchowi i znacznie wydatniej zmniejszający
wahania kulki korkowej niż ołowianej, ale nie czyniący częstszymi
jednych od drugich, nawet gdy łuki przebywane przez korek wynosiły
tylko pięć do sześciu stopni a łuki ołowiu pięćdziesiąt do
sześćdziesięciu stopni, dokonywane jednak zawsze w tym samym czasie.
SIMPLICIO: Jeżeli tak jest, to dlaczegóż by prędkość ołowiu nie była
większą niż korka, skoro jeden przebywał 60o gdy drugi w tymże czasie
zaledwie 6o.
SALVIATI: Ale cóż byście powiedzieli, panie Simplicio, gdyby
oba w równych czasach przebywały swe drogi, nawet jeżeli by korek przy
30° odchylenia miał do przebycia 60°, a ołów przy 2° tylko 4°? Czyż
nie szybszym byłby korek? a doświadczenie stwierdza, że tak się dzieje;
więc zauważcie: odchylając wahadło ołowiane np. na 50° od pionu i
poruszając je swobodnie, to opisze ono z drugiej strony pionu prawie
50°, razem 100°, z powrotem zaś łuk trochę mniejszy aż po wielu
wahaniach dojdzie do spoczynku. Każde z tych wahań odbywa się w czasie,
który pozostaje stale równy, czy to przy 90° czy przy 50°, 20°, 10° lub
4°, tak że prędkość wciąż się zmniejsza, bo w równych czasach opisane
zostają coraz mniejsze łuki. Podobne a nawet zupełnie takie samo
zjawisko przedstawia korek, zawieszony na sznurku tej samej długości,
tylko że on po mniejszej liczbie wahań dochodzi do spoczynku, jako mniej
zdolny, z powodu swej lekkości, do pokonywania oporu powietrza: tak
więc wszystkie wahania odbywają się w równych czasach i tych samych co i
wahania ołowiu. Prawdą więc jest, że podczas gdy ołów przebywa łuk
50°, to korek tylko 10° i korek porusza się wolniej od ołowiu, lecz
zdarza się znów przeciwnie, że korek przebywa 50° a ołów 10° lub 6° i
tym sposobem w różnych czasach raz szybszym jest ołów, drugi raz korek;
ale jeżeli te ciała w równych czasach opisują równe tuki, wtedy można
powiedzieć na pewno, że ich prędkości są równe.
SIMPLICIO: Wydaje mi się i nie wydaje, aby ta rozprawa była
konkludującą i czuję w umyśle takie zamieszanie, że zdaje mi się, jakby
jedno i drugie ciało poruszało się raz prędzej, drugi raz wolniej i nie
mogę sobie jasno wytłumaczyć, żeby ich prędkości były zawsze równe.
SAGREDO: Pozwól mi, pan, panie Salviati, odpowiedzieć dwa
słowa. Powiedźcie mi, panie Simplicio, czy przyjmujecie za pewne, że
prędkości korka i ołowiu są równe każdorazowo, gdy te ciała wychodzą
oba w tej samej chwili ze stanu spoczynku i, poruszając się po tej samej
pochyłości, przebywają równe przestrzenie w równych czasach?
SIMPLICIO: O tym nie można wątpić ani temu przeczyć.
SAGREDO: Niech więc będą wahadła, z których każde
opisuje 60°, lub 50°, lub 30°, lub 10°, lub 8°, 40°, 20° i jeżeli oba biegną 60°, to
przebywają je w tym samym czasie: łuk 50° także jedno i drugie w tym
samym czasie jak również łuki 30°, 10° i inne: stąd więc się wnioskuje,
że prędkość ołowiu na łuku 60° jest równa prędkości korka na tym samym
łuku 60°, i że prędkości na łuku 50° są także sobie równe itd. Ale nie
utrzymuje się, że prędkość przy 60° jest równa prędkości przy 50°, ani
ta ostatnia prędkość przy 30°, lecz że przy łukach mniejszych prędkości
są zawsze mniejsze; toteż widzimy to samo ciało zużywające tyleż czasu
na przebieżenie 60°, jak i łuków 50° lub 10° i w ogóle łuków każdej
wielkości. Chociaż więc korek i ołów biegną z wciąż mniejszemi
prędkościami, im mniejsze przebywają łuki, nie zmienia to jednak ich
zgodności w utrzymywaniu jednakowych prędkości przy przebywaniu
jednakowych tuków. Powiedzieć to chciałem więcej dla zobaczenia, czy
dobrze zrozumiałem wykład p. Salviatiego, niż dlatego, abym
przypuszczał, że p. Simplicio da lepsze objaśnienie od tych, jakie dał
p. Salviati, który zawsze mówi tak zupełnie jasno i nie tylko podnosi
pozorne trudności, ale rozwiązuje istotne zagadki natury, z
rozważaniami, obserwacjami i badaniami, które każdemu są dostępne; dało to sposobność (jak o tym od wielu słyszałem) jednemu z
cenionych profesorów lekceważyć jego nowości, utrzymując, że są
marne i na zbyt niskich i popularnych oparte podstawach, tak jakby
najwięcej uwielbianymi i najcenniejszymi właściwościami nauk
doświadczalnych nie było właśnie wynajdywanie i wyciąganie ich z zasad
najwięcej znanych, zrozumianych i przyjętych przez wszystkich. Ale
przestańmy karmić się tą lekką strawą i w przypuszczeniu, że p.
Simplicio uspokoił się co do tego, że ciężkość ciał nie wywołuje
różnicy prędkości, tak że przy różnej ciężkości wszystkie jednakowo się
poruszają, proszę, aby p. Salviati zechciał nam powiedzieć, na czym
polegają zauważone i widoczne nierówności ruchu; a także odpowiedzieć na replikę pana Simplicia, z którą się zgadzam
i według której nie tylko kula armatnia porusza się prędzej od ziarnka
śrutu, choć z małą różnicą prędkości, czemu przeciwstawiam ciała
jednakowej materii, z których większe spadają w ciągu mniej niż jednego
uderzenia pulsu, w połowie tego czasu, podczas gdy inne mniejsze nie
spadną i w ciągu godziny, albo czterech albo i dwudziestu; jak się to
dzieje z kamieniami i nadzwyczajnie miałkim piaskiem, zawieszonym w
mętnej wodzie, który w tym ośrodku opada na dwa
łokcie w ciągu wielu godzin, podczas gdy niewielkie kamienie spadają w
ciągu jednego uderzenia pulsu.
SALVIATI: Że ośrodek więcej opóźnia ciała gatunkowo lżejsze, to było
już powiedziane i objaśnione zmniejszeniem ciężaru. Ale dlaczego ten sam
ośrodek rozmaicie zmniejsza prędkość ciał, różniących się tylko
wielkością, przy jednakowym materiale i kształcie, to się da objaśnić
tylko badaniem subtelniejszem od tego, w którym wystarczało do
objaśnienia, że ciało jest większe, albo że ruch ośrodka przeciwny
ruchowi ciała zmniejsza jego prędkość. Przyczynę obecnie roztrząsanego
zjawiska upatruję w spotykanych na powierzchniach ciał stałych
chropowatościach i porowatościach, które to nierówności uderzają o
powietrze lub inny ośrodek otaczający, skutkiem czego dochodzi do nas
brzęczenie ciał, nawet gdy są o ile można zaokrąglone; podczas gdy
bardzo prędko biegną w powietrzu, to nie tylko brzęczą, ale piszczą i
świszczą, jeżeli mają znaczniejsze wgłębienia i wypukłości. Przy
kręceniu na tokarni każde ciało okrągłe wytwarza trochę wiatru. Ale co
więcej? czyż nie słyszymy znacznego brzęczenia, nawet w tonie dość
ostrym, jakie sprawia bąk kręcący się na ziemi z wielką szybkością? Ton
piszczałki jest tym niższy, im wolniej była wiercona: dowodzi to, że
chropowatości uderzają o powietrze, jakkolwiek mała jest ich
powierzchnia. Toteż nie można wątpić, że przy spadku ciał, ocierających
się o płyn, który je otacza, powstaje zwalnianie prędkości tym większe,
im powierzchnia będzie większą od powierzchni ciał mniejszych,
porównywanych z większymi.
SIMPLICIO: Zatrzymajcie się proszę, bo zaczyna mi się mieszać: gdyż,
jeżeli godzę się na to, że tarcie ośrodka o powierzchnię opóźnia ruch, i
to tym (ceteris paribus) więcej im
większa jest powierzchnia, to znów nie
rozumiem, dlaczego powierzchnie mniejszych ciał nazywacie większymi; i
dalej, jeżeli, jak mówicie, większa powierzchnia doznaje większego
oporu, to właśnie większe ciała więcej się winny opóźniać, a przecież
tak się nie dzieje: ale tę trudność łatwo usunąć, gdy się powie, że większe
ciała mają wprawdzie większe powierzchnie, ale także i większy ciężar,
tak że przeszkody przy większej powierzchni nie mają jednak tego
wpływu, co przeszkody przy małej powierzchni i małym ciężarze, więc
prędkość większego ciała nie może być mniejsza. Nie widzę przeto
przyczyny, dla której by ustawała równość prędkości, bo gdy się zmniejsza
ciężar, zmniejsza się także działanie opóźniające powierzchni.
SALVIATI: Odpowiem razem na wasze zarzuty. Zgadzacie się na to, panie
Simplicio, że mając dwa równe ciała, jednakowej materIi i kształtu (które
niewątpliwie równie prędko będą się poruszały), jeżeli się zmniejszy
jednakowo tak ciężar jednego, jak i jego powierzchnie (przy czym kształt
pozostaje nie zmieniony), to nie zmniejszy się przez to jego prędkości.
SIMPLICIO: Zdaje mi się, że tak być powinno, gdyż przyjmujemy, że
większy i mniejszy ciężar nie posiadają różnych prędkości.
SALVIATI: Tego też nie utrzymuję i jednocześnie trzymam się waszego
wniosku, że jeżeli ciężar zmniejsza się w większej proporcji niż
powierzchnia, to może powodować wciąż rosnące opóźnienie ruchu, im
większe będzie zmniejszanie ciężaru w stosunku do zmniejszania
powierzchni.
SIMPLICIO: Przeciwko temu nie mam żadnego sprzeciwu.
SALVIATI: Wie pan, panie Simplicio, że nie można zmniejszać
powierzchni ciała w jednakowym stosunku z ciężarem, przy utrzymywaniu
wciąż podobnego kształtu. Bo ciężar zmniejsza się razem z objętością, a
jeżeli objętość zmniejszy się więcej niż powierzchnia, to i ciężar
więcej od powierzchni zostanie zmniejszony. Ale geometria uczy, że o
wiele większy jest stosunek objętości dwóch ciał podobnych od stosunku
powierzchni. Dla bliższego objaśnienia weźmy przykład. Wyobraźmy sobie
sześcian o dwucalowej krawędzi, to każda jego ściana będzie miała
cztery cale kw., a sześć ścian dwadzieścia cztery cale kw. Trzema
przecięciami podzielmy ten sześcian na osiem małych sześcianów o
krawędzi jednocalowej i ścianie jednego cala kw., to powierzchnia małego
sześcianu wynosić będzie sześć cali kw., podczas gdy powierzchnia
większego była 24 cali kw. Powierzchnia więc zmniejszyła się w stosunku
1/4,
a objętość w stosunku 1/8: objętość więc, a z nią
i ciężar, zmniejszają się znacznie więcej niż powierzchnia. A jeżeli
podzielić jeszcze mały sześcian na osiem mniejszych, to każdy z nich
będzie miał półtora cala kw. powierzchni, a więc 1/16 powierzchni
wielkiego sześciana a objętość 1/64. Widzicie więc, jak przy dwóch tylko
podziałach objętość zmniejsza się cztery razy więcej niż powierzchnia; jeżeli zaś dalej dzielić będziemy, aż dojdziemy do drobnego proszku,
to objętość zmniejszy się sto i więcej razy więcej od powierzchni. A
to, co widzieliście z sześcianem, dzieje się także z innymi podobnemi
bryłami, których objętości stoją w półtoracznej proporcji do powierzchni. Widzicie
więc, w jak znacznie większej proporcji wzrosła przeszkoda, przy
zetknięciu poruszającego się ciała małego z ośrodkiem, niż ciała
większego; oprócz tego jest zapewne chropowatość: w małych
powierzchniach proszku nie mniejsza aniżeli w większych ciałach, które
bywają starannie wygładzone: zauważcie przy tym, jak bardzo jest
potrzebne, aby ośrodek był płynny i zupełnie nie stawiał oporu, żeby tak
wątłą siłą mógł być otwierany i ustępował dla umożliwienia przejścia.
Widzicie więc, panie Simplicio, że się nie myliłem mówiąc, że
powierzchnia małych ciał jest wielka w porównaniu z powierzchnią ciał
wielkich.
SIMPLICIO: Jestem całkowicie przekonany i zdaje mi się, że, gdybym
miał na nowo rozpoczynać moje studia, poszedłbym za radą Platona i
zaczynałbym od matematyki, gdyż ta postępuje bardzo skrupulatnie,
przyjmując za rzecz pewną to tylko, co jest ściśle dowiedzione.
SAGREDO: Miałem wielką przyjemność w tej rozmowie, ale zanim
pójdziemy dalej, pragnąłbym zrozumieć jedno orzeczenie, które mi się
wydało nowe, gdy przed chwilą powiedzieliście, że objętości ciał
podobnych mają się do siebie w stosunku półtoracznym powierzchni;
jakkolwiek bowiem dobrze zrozumiałem twierdzenie i dowodzenie, że
powierzchnie ciał podobnych stoją do siebie w podwójnym stosunku boków
i drugie, że objętości tychże ciał stoją do siebie w potrójnym stosunku
tychże boków, ale o stosunku objętości do powierzchni nie przypominam
sobie, aby było co mówione.
SALVIATI: Waszmość sama sobie odpowiada, a oświadcza, że
wątpi. Gdy jedno jest potrójne, a drugie podwójne, to czyż pierwsze nie
jest półtoracznym drugiego? Oczywiście że tak. Więc ponieważ
powierzchnie stoją w podwójnym stosunku do linii, a objętości w
potrójnym, to czyż nie możemy powiedzieć, że objętości stoją w
półtoracznym stosunku do powierzchni?
SAGREDO: Rozumiem to doskonale. Ale, choćbym jeszcze nie jedno miał
do zauważenia, oddaliłoby to nas jeszcze więcej od wytkniętego celu,
tj. od objaśnienia wytrzymałości na złamanie; toteż, jeżeli pozwolicie, może teraz do tego przyjdziemy, co było
postawione na początku.
SALVIATI: Masz pan słuszność, ale różne dotąd podniesione kwestie
zabrały nam tyle czasu, że dziś już mało co tylko mówić będziemy mogli o
tej głównej kwestii, pełnej dowodzeń geometrycznych, które muszą być z
uwagą rozpatrywane; może więc byłoby lepiej odłożyć rozmowę do jutra,
tak z tego powodu, jak i dlatego, że mógłbym przynieść ze sobą niektóre
pisma, w których zestawiłem w porządku wszystkie do tego się odnoszące
twierdzenia i zadania, gdyż przy całej pamięci nie mógłbym sobie ich
przypomnieć z potrzebną metodą.
SAGREDO: Doskonale się pogodzę z tą radą i to tym chętniej, że
na zakończenie dzisiejszego posiedzenia będę miał czas prosie o
rozjaśnienie niektórych wątpliwości dotyczących ostatnio traktowanego
przedmiotu. Jedną z nich jest, czy opór ośrodka może wystarczać do
zniweczenia przyspieszenia ciał z najcięższej materii, wielkiej
objętości i kulistego kształtu; wybieram ten kształt dlatego, że kula
ma najmniejszą powierzchnię, a zatem mniej jest narażona na opóźnienie.
Drugą kwestią jest ruch wahadła i to z dwóch względów: po pierwsze, czy
rzeczywiście wszystkie wahadła, wielkie, średnie i małe, wahają się w
ściśle równych czasach i powtóre w jakiej proporcji są do siebie czasy
wahań wahadeł nierównej długości.
SALVIATI: Pytania są piękne, gdy jednak przy każdej prawdzie napotyka
się zawsze nowe interesujące wnioski, wątpię bardzo, aby reszta
dzisiejszego dnia wystarczyła nam dla roztrząśnienia wszystkich.
SAGREDO: Jeżeli one tak piękne, jak dotąd poruszane, to wolę im
poświęcić tyle dni, ile nam dziś godzin zostaje do nocy i sądzę, że pan
Simplicio nie będzie znudzony tą rozmową.
SIMPLICIO: Oczywiście nie, a zwłaszcza, jeżeli rozbierane
będą kwestie odnoszące się do rzeczy przyrodzonych, których nie
dotykali inni filozofowie.
SALVIATI: Przejdziemy więc do pierwszego twierdzenia, orzekającego,
bez żadnej wątpliwości, że nie ma kuli tak wielkiej i ciężkiej, której by
przyspieszenia nie zmniejszał opór ośrodka choćby jak najrzadszego i
przy dalszym ruchu nie sprowadzał go do jednostajności, czego
jasny dowód daje nam samo doświadczenie. Bo gdyby ciało spadające
dochodzić mogło w dalszym swym ruchu do jakiegokolwiek stopnia
prędkości, to żadna prędkość udzielona mu przez motor zewnętrzny nie
mogłaby być tak wielka, aby się ono jej nie pozbyło i nie straciło
wskutek oporu ośrodka. Np. kula armatnia, spadająca z wysokości 4 łokci,
nabywa 10 stopni prędkości i jeżeli z tą prędkością spada do wody, to
gdyby opór wody nie mógł pokonywać tego impetu (impeto), prędkość będzie się
zwiększać, a przynajmniej trwać aż do dna; co nie następuje, a przeciwnie,
woda, choćby tylko parę łokci głęboka, zwalnia bieg i osłabia do tego
stopnia, że koryto rzeki lub jeziora otrzyma bardzo słabe tylko
uderzenie. Jasne w tym jest, że prędkość, którą woda na bardzo krótkiej
drodze potrafiła zniszczyć, nie mogłaby być nabyta nawet na głębokości
1000-ca łokci. I dlaczego tolerowalibyśmy jej nabycie na 1000-cu łokci,
podczas gdy na 4-ch została zniszczona? Ale więcej jeszcze, czyż nie
widzimy, jak niezmierny impet kuli armatniej bywa całkowicie zniesiony w
paru łokciach wody, że bez istotnego uszkodzenia okrętu zaledwie takowy
dziurawi? Albo powietrze, pomimo swej ustępliwości, może hamować
prędkość spadającego dość ciężkiego ciała, co moglibyśmy udowodnić
podobnymi doświadczeniami; bo jeżeli z wierzchołka bardzo wysokiej
wieży strzelimy ku ziemi, to kula mniej głęboko w nią wejdzie niż
gdyby strzał nastąpił z wysokości czterech lub sześciu łokci; dowód
oczywisty, że impet, z którym leciała kula z lufy na wierzchu wieży,
zmniejszał się w powietrzu; spadek więc z jak największej wysokości nie
wystarcza do nabycia impetu, który odejmuje powietrze, gdy ten impet w
jakikolwiek sposób został udzielony. Podobnie uszkodzenie, jakie robi
w murze uderzenie kuli, wystrzelonej z muszkietu w odległości
dwudziestu łokci, nie sądzę, aby mogło być zrobione strzałem pionowym z
jakiejkolwiek wysokości. Dlatego sądzę, że każde przyspieszenie ciała
naturalnego ma swój koniec i że ostatecznie, skutkiem oporu ośrodka,
ruch sprowadzony zostaje do jednostajności, w której następnie wciąż
pozostaje.
SAGREDO: Doświadczenia wydają mi się zupełnie zadowalające,
zarzucić by można tylko, czy dałyby się sprawdzić z
ciałami bardzo wielkimi i ciężkiemi i czy kula armatnia przychodząca z
księżyca lub z najwyższej warstwy powietrza nie sprawiłaby silniejszego
uderzenia niż wychodząca z armaty.
SALVIATI: Niewątpliwie można wszystkiemu oponować i nie
wszystko da się dowieść doświadczeniem, w tym zarzucie wszakże, zdaje mi
się, że jedna rzecz winna by być wzięta pod uwagę: a mianowicie,
bardzo jest prawdopodobne, że ciało z wysokości
spadające nabywa takiego impetu dochodząc do ziemi, jaki by wystarczał,
aby się podniosło do tej samej wysokości, co widzimy wyraźnie na
wahadle, które na 50° do 60° odchylone od pionu nabywa taką prędkość i
własność, która akuratnie wystarcza, aby się równie wysoko podniosło,
pomijając niewielką stratę spowodowaną oporem powietrza. Aby więc kulę
armatnią podnieść na wysokość, która by wystarczała do nabycia tak
wielkiej prędkości, jak przy wyjściu z działa, winnob y wystarczać, aby
ją wystrzelić pionowo z tegoż działa i zaobserwować, czy spadając sprawi
to samo uderzenie, jak przy strzale z bezpośredniego sąsiedztwa;
sądzę, iż prawdopodobnie różnica nie byłaby wielka. Sądzę przeto, że
prędkość, jaką ma kula armatnia tuż przy wyjściu z działa, będzie taka,
jakiej nigdy nie pozwoliłby nabyć opór powietrza, choćby kula spadała
swobodnie wychodząc ze spoczynku, z jak największej wysokości.
Przechodzę teraz do drugiej kwestii, dotyczącej wahadła, przedmiotu,
który wielu wydaje się dość oschłym, a zwłaszcza tym filozofom, którzy
są stale zajęci badaniem najgłębszych zadań przyrody; ale ja nie będę
gardził tym zadaniem, zachęcony przykładem samego Arystotelesa, którego
zawsze podziwiam, że się wszystkiem zajmuje, co tylko godne jest uwagi;
mógłbym wam także zakomunikować niektóre myśli dotyczące muzyki,
przedmiotu najszlachetniejszego, o którym wielu pisało znakomitych
ludzi, a nawet i sam Arystoteles rozważał odnośne a liczne ciekawe
zadania; tak że jeżeli Wam wyłożę, na podstawie łatwych a dowcipnych
doświadczeń, niektóre zadziwiające zjawiska w dziedzinie dźwięków, mani
nadzieję, że rozważanie moje przyjmiecie.
SAGREDO: Będziemy za nie bardzo wdzięczni i, co do mnie, spełni
się moje gorące życzenie, gdyż, zajmując się wszystkiemi instrumentami
muzycznYmi i rozmyślając wiele nad współdźwięcznością, nie mogłem nigdy
pojąć, skąd to pochodzi, że jedno mnie zadowala, a drugie nie tylko, że
nie zadowala, ale nawet w najwyższym stopniu się nie podoba. Znane
zadanie dwóch strun naciągniętych do równodźwięczności, z których, gdy
jedna dźwięk wydaje, to druga się porusza i tak samo dźwięczy, nie jest
dla mnie jasne, a także nie rozumiem dobrze formy współdźwięku i innych
szczegółów.
SALVIATI: Zobaczmy, czy nasze wahadła nie mogą nam dostarczyć
rozwiązania tych wszystkich wątpliwości. A co do pierwszej, mianowicie,
czy ściśle jest prawdziwe, że wahadło wszystkie swoje wahania wielkie,
średnie i małe uskutecznia w równych czasach, powołuję się tu na wywody
naszego Akademika, który wykazał, że ciało spadające wzdłuż cięciwy
jakiegokolwiek łuku, zawsze spada w ciągu tego samego czasu, czy ten
łuk ma całe 180°, czy też 100° 60°, 2°, 1/2° albo
4°; przy czym wszystkie dochodzą do najniższego punktu łuku. Następnie,
ciała spadające wzdłuż łuków tych cięciw podnoszących się nad poziom nie
więcej jak na 90°, spadają, jak wykazuje doświadczenie, wszystkie w
równych czasach, ale nieco krótszych niż przy spadku po cięciwach;
zjawisko tym więcej zadziwiające, że można było oczekiwać skutku
przeciwnego. Jeżeli bowiem jednakie są początki i końce ruchów, a linia
prosta jest najkrótszą drogą między tymi punktami, wydawałoby się
racjonalne, że ruch po tej linii winien trwać najkrócej, a jednak tak
nie jest; najkrótszy czas i najprędszy ruch odbywa się wzdłuż łuku,
którego ta prosta jest cięciwą. Przy wahadłach różnej długości, czasy
mają się do siebie tak, jak pierwiastki kwadratowe z długości, albo inaczej,
długości mają się do siebie tak, jak kwadraty z czasów wahań;
gdy jedno
wahadło ma się poruszać dwa razy wolniej niż drugie, to musi być cztery
razy dłuższe: jeżeli chcecie np., aby czas jednego wahania wahadła byt
dwa razy większy od czasu wahania drugiego wahadła, to trzeba, aby jego
długość była cztery razy większa, od długości drugiego wahadła. A gdy
podczas jednego wahania jednego wahadła, drugie zrobi trzy wahania, to
długość pierwszego musi być dziewięć razy większa od długości drugiego.
Wynika stąd, że długości wahadeł mają się do siebie w stosunku kwadratów
z liczby wahań dokonanych w ciągu tego samego czasu.
SAGREDO: Więc, jeżeli dobrze zrozumiałem, to mogę szybko
obliczyć długość wahadła niezmiernie wielkiego, nawet gdyby jego punkt
zawieszenia był niewidzialny, jeżeli tylko obserwować mogę jego koniec
dolny. Dość będzie, gdy zawieszę u spodu dość znaczny ciężar i wprawię
go w ruch, to w jedną, to w drugą
stronę, a przyjaciel zacznie liczyć wahania, ja zaś równocześnie liczyć
będę wahania drugiego wahadła, którego długość jest ściśle równa
jednemu łokciowi, z liczb wahań tych wahadeł, dokonywanych w tym samym
czasie, znajdę długość pierwszego wahadła; jeżeli np. założymy, że
mój przyjaciel policzy t dwadzieścia wahań długiego wahadła, a ja
policzyłem dwieście czterdzieści mojego łokciowego; to, podnosząc do
kwadratu liczby 20 i 240, otrzymamy 400 i 57600; powiem wtedy, że długi sznur zawiera 57600 miar takich, jakich jest
400 w łokciu; a więc, dzieląc 57600 przez 400, otrzymamy długość
wielkiego wahadła 144 łokci.
SALVIATI: Nie pomylicie się ani na piędź, zwłaszcza jeżeli brać
będziecie wielkie liczby wahań.
SAGREDO: Waszmość daje mi często sposobność podziwiania
bogactwa, a zarazem największej hojności natury, gdy z prostych, prawie
trywialnych rzeczy wyciąga wiadomości
wysoce ciekawe, nowe i dalekie od wszelkiej imaginacji.
Pewno tysiące
razy obserwowałem wahania żyrandoli, wiszących w kościołach na bardzo
długich sznurach, niezauważone przez nikogo, lecz nie wyciągnąłem nic
więcej z tych obserwacji, jak tylko nieprawdopodobieństwo poglądu tych,
którzy mniemali, że podobne ruchy utrzymywane są przez ośrodek
otaczający, a więc przez powietrze; bo zdawało mi się, że powietrze
miałoby wielkie zadanie do spełnienia a jednocześnie małą robotę, tracąc
godziny i godziny na popychanie, to w jedną to w drugą stronę
zawieszonego ciężaru z taką regularnością, ale, żebym się miał
dowiedzieć, że jedno i to samo ciało, zawieszone na stułokciowym
sznurze i odchylone czy to na 90° czy na 1° lub 1/2°,
tyleż czasu potrzebuje na przebieżenie małego łuku jak i wielkiego, temu
nie mogę uwierzyć i wciąż wydaje mi się to niemożliwe. A teraz ciekaw
jestem usłyszeć owe zjawiska dźwiękowe, które nie przestają mnie
niepokoić.
SALVIATI: Przede wszystkiem trzeba zaznaczyć, że każde wahadło ma tak
stały i określony czas wahań, że nie można go w żaden sposób poruszać w
innym okresie jak w tym jedynym jego naturalnym. Jeżeli wezmę w rękę
sznurek, na którym zawieszony jest ciężar i będę się starał jakimkolwiek
sposobem zwiększać lub zmniejszać liczbę jego wahań, będzie to próżna
fatyga; przeciwnie znów, wahadłu w spoczynku, choćby najcięższemu,
możemy przez jedno nań dmuchnięcie nadać ruch i to tym większy jeżeli
powtarzać będziemy dmuchnięcia w chwilach odpowiadających wahaniom; jeżeli pierwszem dmuchnięciem odchylimy wahadło od pionu na
1/2 cala,
to dodając drugie dmuchnięcie wtedy, gdy wahadło ku nam wróciło po
ukończeniu pierwszego wahania, nadamy mu nowy ruch, a gdy tak wciąż
dmuchać będziemy w chwilach właściwych, a nie wtedy gdy wahadło ku nam
idzie (bo to hamowałoby ruch a nie pobudzało), to tymi wieloma popędami (impulses)
nadać mu możemy taki impet (impeto), ze zużyta by być musiała siła znacznie
większa od jednorazowego dmuchnięcia, aby wahadło zatrzymać.
SAGREDO: Dzieckiem jeszcze będąc, widziałem jak jeden człowiek,
przez popychanie we właściwych czasach wielkiego dzwonu, wywoływał
dzwonienie, a, żeby je zatrzymać, wieszało się na linie czterech do
sześciu ludzi i nieraz lina podnosiła wszystkich w górę, gdyż nie mogli
wstrzymać impetu, jaki nadał jeden człowiek regularnymi popchnięciami.
SALVIATI: Przykład ten również pożytecznie służyć mi może do
objaśnienia zadziwiającej zagadki struny cytry lub cymbała, która
porusza i rzeczywiście robi dźwięczną inną strunę zgodną z nią co do
tonu albo różniącą się o oktawę lub kwintę. Dotknięta struna
rozpoczyna i prowadzi dalej swe drgania przez cały czas, dopókąd trwa jej
dźwięk: te drgania wprawiają powietrze w ruch, drżenie jego rozszerza
się dalej i uderza o wszystkie struny tegoż samego instrumentu a także
innych sąsiednich: struna nastrojona do unisona z dotkniętą, usposobiona
do dokonywania swych drgań w tym samem tempie, nabywa w końcu drgania
takiegoż jak pierwsza i widzicie wyraźnie rozszerzenie się jej drgań
według okrsu struny poruszającej. Falowanie to, rozszerzając się w
powietrzu, wprawia w ruch i drganie nie tylko struny, ale jakiekolwiek
inne ciało skłonne do drgania, które drgać będzie przez cały czas
drgania struny: tak że jeżeli na brzegu instrumentu położymy kawałki
szczeci lub innej lekkiej materii, to ujrzymy drganie, podczas
dźwięczenia cymbału, to jednego to drugiego ciała, stosownie do tego,
która struna drga jednocześnie ze struną poruszoną, inne zostają w
spokoju przy odgłosie tej struny, a poruszają się przy odgłosie innej.
Gdy mocno pociągniemy smyczkiem po grubej strunie wiolonczeli, zbliżając
do niej kieliszek z cienkiego i gładkiego szkła, to jeżeli ton struny
jest unisono z tonem kieliszka, ten będzie drgał i głośno dźwięczał. Jak
przez otaczający ośrodek rozszerzają się drgania dźwięczącego ciała,
zobaczyć można, gdy się rozdźwięcza kieliszek, napełniony wodą, przez
pocieranie palcem po brzegu; widzi się wtedy falowanie wody jak
najregularniejsze a lepiej jeszcze zobaczy się to zjawisko, gdy nóżka
kieliszka stoi na dnie dużego naczynia, napełnionego wodą po brzeg
kieliszka, który także wprawia się w dźwięczenie pocierając palcem po
brzegu; widzi się wtedy jak najregularniejsze zmarszczki rozchodzące się
z wielką szybkością, daleko wokół kieliszka, a nawet zdarzyło mi się
widzieć, przy dość dużym kielichu, że ton skakał o oktawę wyżej i w tej
samej chwili każda z fal rozdzielała się na dwie: zjawisko wyraźnie
pokazujące, że forma oktawy jest zdwojeniem.
SAGREDO: l mnie się to samo nieraz zdarzyło, sprawiając przyjemność
a także pożytek; bo pozostając długo niepewnym co do tej formy
współdźwięczności nie sądziłem, aby jej stosunek, podawany zwykle
przez autorów piszących uczenie o muzyce, był zadowalający.
Mówili
oni, że diapazon czyli oktawa stoi w podwójnym, diapenta, albo jak ją
nazywają kwinta, w półtoracznym stosunku, bo struna monochordu,
dźwięcząca cała, a potem dźwięcząca w połowie, przy postawionym koziołku
w środku daje oktawę, a jeżeli koziołek postawiony zostanie na
trzeciej części długości struny daje kwintę, a więc oktawę przedstawia
stosunek 1/2, a kwintę 2/3. Uzasadnienie to nie
wydało mi się wystarczające dla ustalenia, że podwójność i
półtoracznośó są formami naturalnemi diapazonu i diapenty. A motywy
moje były następujące: w trojaki sposób podnosić możemy ton struny,
przez skrócenie, większe naciągniecie czyli napięcie i zmniejszenie
grubości. Przy równm napięciu i grubości otrzymujemy oktawę przez
skrócenie do połowy, tj. uderzając raz całą strunę, a drugi raz jej
połowę. Przy równej długości i grubości, otrzymujemy oktawę, naciągając
więcej strunę, ale nie wystarcza tu zdwojenie siły lecz, trzeba wziąć
siłę cztery razy większą; jeżeli struna była naciągnięta jednym funtem,
to potrzeba użyć czterech funtów dla otrzymania oktawy. Wreszcie, przy
równej długości i jednakowym napięciu, widzimy, że, aby struna przez
zmniejszenie grubości dawała oktawę, to trzeba, aby była cztery razy
cieńsza od dającej ton niższy. A to, co mówię o oktawie, tj. że się
jej formę bierze z napięcia, z grubości lub z podwójnego stosunku
długości, odnosi się także do innych interwalów muzycznych; jeżeli
bowiem ze stosunku długości wypada półtoraczność, tj. raz cała struna,
drugi raz dwie trzecie, to chcąc ją otrzymać przez zmianę napięcia albo
grubości, wziąć trzeba kwadrat ze stosunku półtoracznego; tj. jeżeli np. struna dająca ton niższy naciągnięta była czterema
funtami, to dla tonu wyższego trzeba nie sześciu ale dziewięciu funtów,
a co do grubości, trzeba strunę niższą uczynić grubszą od wyższej w
stosunku 9 do 4 aby otrzymać kwintę. Wobec tych ścisłych doświadczeń,
wydało mi się zupełnie nieuzasadnionem przyjmowanie razem z dowcipnymi
filozofami, dla formy oktawy stosunku 1/2
zamiast 1/4, a dla kwinty 2/3 zamiast 4/9. Ale ponieważ jest niemożliwe liczenie drgań struny, zbyt licznych
podczas dźwięczenia, byłbym w ciągłej wątpliwości, czy rzeczywiście,
przy wyższym tonie oktawy, struna dokonuje w tym samym czasie dwa razy
tyle drgań co przy niższym, gdyby nie to, że nieustanne fale przy
dźwięczącym i drgającym kieliszku wykazały mi wyraźnie, jak w tej
samej chwili, gdy dał się słyszeć jeden raz ton wyższy, powstawały nowe
fale mniejsze, które jak najściślej przepołowiały każdą z fal
pierwotnych.
SALVIATI: Piękne to doświadczenie, przy którym rozróżniać można
poszczególne drgania, wychodzące od drgającego ciała; drgania te rozchodząc się w powietrzu, wprawiają w ruch nasz bębenek
uszny i stają się dźwiękiem w naszej duszy. Ale ponieważ widziałem i
zaobserwowałem, że wzburzenie w wodzie trwa tylko dopóty, dopóki
pociągamy palcem po kieliszku, a nawet w ciągu tego czasu nie bywa
stałe, a tylko to powstaje to znika, czyż więc nie byłoby rzeczą piękną,
gdyby można było uczynić drgania długotrwałymi, przez miesiące i lata,
tak żeby można było je mierzyć i łatwo liczyć?
SAGREDO: Istotnie, taki wynalazek ceniłbym bardzo.
SALVIATI: Wynalazek był dziełem przypadku, a moją tylko była
obserwacja, poważna i cenna jakkolwiek nie pochodząca z głębokiego
rozważania, lecz z roboty dość pospolitej. Skrobiąc ostrem dłutem
żelaznym płytę mosiężną, dla usunięcia plam, przy szybkim poruszaniu
dtuta usłyszałem raz i dwa między wieloma ślizgami i świstami, gwizd
bardzo mocny i wyraźny, a gdy spojrzałem na płytę, spostrzegłem długi
szereg cienkich równoległych kresek w ściśle równych odstępach. Przy
dalszem skrobaniu wielokrotnie zauważyłem, że tam tylko, gdzie się ten
gwizd powtarzał, dłuto robiło takie kreski, tam zaś, gdzie skrobanie
dawało się słyszeć bez gwizdu, nie było żadnego śladu podobnych kresek.
Powtarzając nieraz tą zabawę, skrobiąc to z większą, to z mniejszą
szybkością, gwizd odzywał się w tonie wyższym lub niższym i
zauważyłem,
że przy wyższych tonach kreski były gęstsze, a przy niższych rzadsze, a
nawet wtedy, gdy skrobanie przy końcu było szybsze niż przy początku,
ton gwizdu się podnosił, a jednocześnie kreski stawały się więcej
skupione, ale zawsze zupełnie czyste i równo od siebie oddalone; oprócz
tego przy gwiżdżących skrobaniach czułem w dłoni drganie dłuta, a przez
rękę przebywający pewien dreszcz. Widać w rezultacie, że z żelazem
dzieje się to samo co z nami, gdy mówimy cicho a potem wydajemy silny
głos, że wypuszczając oddech bez wydawania dźwięku nie czujemy w gardle
i w ustach żadnego ruchu, w porównaniu z mocnem drganiem, które
odczuwamy w krtani i gardzieli przy wydawaniu głosu, zwłaszcza w
głębokich i silnych tonach. Nieraz zaznaczałem na strunach cymbału dwa
tony jednobrzmiące z dwoma różnymi gwizdami, o których była mowa, a
różnica między nimi wynosiła doskonałą kwintę, gdy zaś zmierzyłem
odległości między kreskami, znalazłem, że 45 kreskom jednego tonu
odpowiadało 30 drugiego; co rzeczywiście odpowiada formie przypisywanej
diapencie. Ale zanim pójdę dalej, muszę ostrzec, że z trzech sposobów
podwyższania tonu, ten, który opieracie na cienkości struny, właściwiej
byłoby odnosić do jej ciężaru. Bo przy jednakowym materiale pozostaje
dla grubości ten sam stosunek, tak że z dwóch strun bydlęcych, musi
jedna być cztery razy grubszą od drugiej, aby dawać oktawę i toż samo ma
miejsce przy obu strunach metalowych. Ale jeżeli chcę otrzymać oktawę z
jednej struny bydlęcej i drugiej metalowej, to stosunek nie będzie
czterokrotny co do grubości, ale trzeba wziąć ciężar cztery razy
większy; tak że struna metalowa nie będzie miała czterokrotnego
przekroju struny bydlęcej ale czterokrotny ciężar i będzie tyle razy
cieńszą od bydlęcej, odpowiadającej wyższej oktawie. Wynika stąd, że,
jeżeli założymy w jednym cymbale struny złote, a w drugim mosiężne i będą
tej samej długości, napięcia i grubości, to ponieważ złoto jest dwa
razy cięższe, struny złote dawać będą ton o kwintę niższy. Tu zauważcie,
że prędkości ruchu więcej się opiera ciężar ciała niż jego wielkość,
odwrotnie niżby można było się spodziewać; gdyż zdawało się, że prędkość
więcej może być hamowana przez opór ośrodka, gdy ciało jest większe i
lżejsze niż gdy jest cięższe i mniejsze; w tym przypadku zaś rzecz się
dzieje zupełnie przeciwnie. Ale wracając do pierwszego, powiadam, że
bezpośredni stosunek formy interwalu muzycznego nie zależy ani od
długości struny, ani od napięcia, ani od przekroju, a tylko od liczby
drgań i uderzeń fal powietrza, dochodzących do bębenka naszego ucha i
które w ciągu tego samego czasu wprawiają ten bębenek w drganie.
Trzymając się tego, możemy ze ścisłością objaśnić, dlaczego jedne
współdźwięki sprawiają nam wielką przyjemność, inne mniejszą, a inne
nawet wielką nieprzyjemność, możemy więc podać przyczynę mniej lub
więcej doskonałej współdźwięczności i dysonansu. Nieprzyjemność tego
ostatniego pochodzi, jak myślę, z niezgadzających się ze sobą drgań,
które wytwarzają dwa różne tony i uderzają niewspółmiernie o nasz
bębenek uszny, a najnieznośniejszymi są rozdźwięki, gdy czasy drgań nie
dają się wyrazić liczbami, ile idzie jednych na ile drugich, jak gdy z
dwóch na jeden ton nastrojonych strun, jedna drga w takiej części
względem drugiej, jak bok kwadratu do przeciwprostokątnej: rozdźwięk
podobny trytonowi albo połowie diapenty. Współdżwięczną i mile brzmiącą
będzie taka para tonów, które uderzać będą w pewnym porządku o bębenek;
a pierwszym warunkiem tego porządku jest, aby liczby uderzeń w ciągu
pewnego czasu były współmierne, tak aby błona bębenka nie znajdowała się
w ciągłym zamieszaniu, poddając się i ulegając wciąż niezgodnym
uderzeniom. Toteż pierwszą i najdoskonalszą współdźwięcznością jest
oktawa, bo każdemu uderzeniu (o bębenek) niższego tonu odpowiadają dwa
wyższego; tak że te dwa wyższe przychodzą równocześnie z jednem niższym
i ze wszystkich uderzeń połowa pada razem, podczas gdy przy unisonie
wszystkie padają razem i o żadnej współdźwięczności nie ma już mowy.
Kwinta jest również przyjemna, bo na każde dwa drgania struny niższej,
struna wyższa daje trzy drgania, skąd wynika, że trzecia część uderzeń
(o bębenek) wyższego tonu schodzi się z uderzeniami niższego, a dwie
samotne przedzielają pary zgodnych; przy kwarcie
przedziela ich trzy. Przy sekundzie na każde
dziewięć uderzeń jedno tylko dochodzi zgodnie z uderzeniem struny
niższej, wszystkie inne są niezgodne, przyjmowane z odrazą przez
bębenek i poczytywane za dysonans przy słuchaniu.
SIMPLICIO: Pragnąłbym większej jasności w tym wywodzie.
 SALVIATI:
Niech będzie (rys. 13) AB długość drgania struny niższej, a CD
struny wyższej, która z poprzednią daje oktawę i niech będzie E środek
AB. Widać, że gdy ruch wychodzi z punktów A i C, to gdy
drganie wyższe dochodzi do D, drugie dojdzie tylko do środka E, który
nie brzmi, nie stanowiąc końca ruchu, a uderzenie będzie tylko w D. Gdy
drganie wraca od D do C, to drugie przechodzi od E do B, i wtedy dwa
uderzenia z B i C dochodzą jednocześnie do bębenka; a gdy drgania tak
następować będą po sobie, to uderzenia będą się na przemian raz spotykać,
a drugi raz nie; ale uderzeniom końcowym towarzyszyć będzie zawsze jedno
z uderzeń C, D, i zawsze to samo; wynika stąd, że gdy A i C uderzają
jednocześnie, to gdy A przechodzi do B, C idzie do D i wraca do C, tak
że pary AC są zawsze te same. Ale jeżeli drgania AB i CD dają diapentę,
to ich czasy mają się do siebie w stosunku półtoracznym i dzielić należy
AB struny niższej na trzy części równe w E i O. Drgania zaczynają się
dawać słyszeć w tej samej chwili w punktach A i C; oczywiście, gdy
uderzenie następuje w D, drganie struny niższej dochodzi do O, a
bębenek otrzymuje uderzenie tylko w D; przy powrocie od D do C, drganie
struny niższej postępuje od O do B i wraca od B do O, wykonywając
uderzenia odosobnione w B, nie wpadające w tempo uderzeń struny wyższej
(co należy zauważyć), bo ponieważ przyjęliśmy równoczesny początek drgań
w A i C, to drugie drganie, które uderzało odosobnione w D, uderzy
wracając o tyle później, ile nam trzeba na przejście od C do D lub od A
do O. Ale uderzenie w B następuje tylko o połowę tego czasu później, bo
OB=1/2 AO; dalej jedno
drganie wraca od O do A, a równocześnie drugie idzie od C do D, tak że
oba uderzają razem w A i D. Podobne okresy następują dalej, ze
wstawieniem dwóch oddzielnych i odosobnionych uderzeń wyższego tonu i
jednego odosobnionego niższego tonu, między dwa odosobnione wyższego.
Jeżeli podzielimy czas na równe małe momenty, to w pierwszych dwóch
momentach od A i od C następuje przejście do O i do D i uderzenie w D,
następnie w trzecim i czwartym momencie powrót od D do C i uderzenie w
C, a jednocześnie ruch od O do B, uderzenie w B i powrót od B do O,
wreszcie w piątym i szóstym momencie drgania od O i C do A i D i
równoczesne uderzenia w obu tych punktach, a na błonie bębenka uderzenia
następują w takim porządku, że jeżeli się spotykają na początku, to po
dwóch momentach następuje odosobnione, po trzecim znów odosobnione i tak
samo po czwartym, a po dwóch następnych dwa uderzenia razem: wtedy okres
jest ukończony i cała anomalia powtarza się wiele razy w następstwie.
SALVIATI:
Niech będzie (rys. 13) AB długość drgania struny niższej, a CD
struny wyższej, która z poprzednią daje oktawę i niech będzie E środek
AB. Widać, że gdy ruch wychodzi z punktów A i C, to gdy
drganie wyższe dochodzi do D, drugie dojdzie tylko do środka E, który
nie brzmi, nie stanowiąc końca ruchu, a uderzenie będzie tylko w D. Gdy
drganie wraca od D do C, to drugie przechodzi od E do B, i wtedy dwa
uderzenia z B i C dochodzą jednocześnie do bębenka; a gdy drgania tak
następować będą po sobie, to uderzenia będą się na przemian raz spotykać,
a drugi raz nie; ale uderzeniom końcowym towarzyszyć będzie zawsze jedno
z uderzeń C, D, i zawsze to samo; wynika stąd, że gdy A i C uderzają
jednocześnie, to gdy A przechodzi do B, C idzie do D i wraca do C, tak
że pary AC są zawsze te same. Ale jeżeli drgania AB i CD dają diapentę,
to ich czasy mają się do siebie w stosunku półtoracznym i dzielić należy
AB struny niższej na trzy części równe w E i O. Drgania zaczynają się
dawać słyszeć w tej samej chwili w punktach A i C; oczywiście, gdy
uderzenie następuje w D, drganie struny niższej dochodzi do O, a
bębenek otrzymuje uderzenie tylko w D; przy powrocie od D do C, drganie
struny niższej postępuje od O do B i wraca od B do O, wykonywając
uderzenia odosobnione w B, nie wpadające w tempo uderzeń struny wyższej
(co należy zauważyć), bo ponieważ przyjęliśmy równoczesny początek drgań
w A i C, to drugie drganie, które uderzało odosobnione w D, uderzy
wracając o tyle później, ile nam trzeba na przejście od C do D lub od A
do O. Ale uderzenie w B następuje tylko o połowę tego czasu później, bo
OB=1/2 AO; dalej jedno
drganie wraca od O do A, a równocześnie drugie idzie od C do D, tak że
oba uderzają razem w A i D. Podobne okresy następują dalej, ze
wstawieniem dwóch oddzielnych i odosobnionych uderzeń wyższego tonu i
jednego odosobnionego niższego tonu, między dwa odosobnione wyższego.
Jeżeli podzielimy czas na równe małe momenty, to w pierwszych dwóch
momentach od A i od C następuje przejście do O i do D i uderzenie w D,
następnie w trzecim i czwartym momencie powrót od D do C i uderzenie w
C, a jednocześnie ruch od O do B, uderzenie w B i powrót od B do O,
wreszcie w piątym i szóstym momencie drgania od O i C do A i D i
równoczesne uderzenia w obu tych punktach, a na błonie bębenka uderzenia
następują w takim porządku, że jeżeli się spotykają na początku, to po
dwóch momentach następuje odosobnione, po trzecim znów odosobnione i tak
samo po czwartym, a po dwóch następnych dwa uderzenia razem: wtedy okres
jest ukończony i cała anomalia powtarza się wiele razy w następstwie.
SAGREDO: Nie mogę dłużej milczeć i muszę objawić zadowolenie,
jakie mi sprawiło tak wyborne uzasadnienie zjawisk, które mnie tak długo
trzymały w ciemności i ślepocie. Teraz rozumiem, dlaczego unisono nie
różni się od jednego pojedynczego głosu: pojmuję dlaczego oktawa jest najlepszym
współdźwiękiem, a przy tym tak
podobna do jednodźwięku, że brzmi jak ten ostatni: podobna jest do
unisonu, bo drgania strun na jeden ton nastrojonych uderzają wszystkie
razem, uderzenia niższej struny zawsze razem z uderzeniami wyższej, a
między nimi równoodległe od obu uderzenie odosobnione, i tak bez
żadnego zamieszania, dlatego też ta współdźwięczność jest zbyt słodka i
mało ożywiona. Za to kwinta ze swoimi kontratempami, ze wstawkami między
pary dwóch połączonych drgań, dwóch drgań odosobnionych struny wyższej i
jednej odosobnionej struny niższej, tej ostatniej następującej w połowie
dwóch poprzednich i w połowie okresu między uderzeniami par drgań,
wywołuje takie miłe łechotanie bębenka, że ożywiając słodycz
deszczykiem kwasu, daje wrażenie zarazem pocałunku i ukąszenia.
SALVIATI: Skoro Waszmościom tak przypadły do gustu te nowości,
podać Warn muszę, w jaki sposób może nie tylko ucho, ale i oko zabawić
się widokiem podobnych wybryków. Zawieście kulki ołowiane albo inne
ciężkie ciała na trzech sznurkach różnej długości, ale takich, że gdy
najdłuższy dokonuje dwóch wahań, to w tym samym czasie najkrótszy robi
ich cztery a średni trzy, a co ma miejsce, gdy najdłuższy ma 16 palm lub
innych miar, średni 9 a najkrótszy 4; gdy wszystkie równocześnie
odchylone zostaną od pionu i puszczone, widzi się nieokreślone
krzyżowanie się sznurków, różnie się schodzących, ale w ten sposób, że
przy każdem czwartem wahaniu najdłuższego wszystkie trzy znajdują się
równocześnie w początku ruchu i zaczyna się taki sam nowy okres; to
pomieszanie wahań jest takie samo, jak czynione na słuchu przez struny
dające oktawę i kwintę. Jeżeli w podobny sposób oznaczymy długość innych
sznurków odpowiednio do wiadomych
współdźwięczących interwałów muzycznych, to otrzymamy znów inne splątanie
ruchów wahadeł, takie jednak, że po pewnej liczbie wahań wszystkie znów
stawać będą równocześnie w punktach wyjścia i razem puszczą się w ruch,
by rozpocząć nowy podobny okres. Ale jeżeli czasy wahań dwóch hib
więcej sznurków są niewspółmierne, tak że nigdy w jednej i tej samej
chwili nie wracają do punktu wyjścia, albo nawet, gdy są współmierne,
wracają po zbyt długim przeciągu czasu i po zbyt wielkiej liczbie
wahań, to oko zostaje zmęczone widokiem tej ciągłej nieregularności, a
ucho z udręczeniem odbiera drgania powietrza wpadające bez żadnego
porządku i regularności.
Ale dokądże to, moi panowie, pozwoliliśmy się
doprowadzić przez te różne kwestie i niespodziewane rozmowy. Noc
nadeszła, z przedmiotu postawionego roztrząsnęliśmy bardzo mało, nic
prawie; tymczasem zboczyliśmy tak z drogi, że zaledwie przypominam sobie punkt wyjścia i
pierwsze rozważania, przyjęte jako hipotezy i podstawy dalszych
rozwiązań.
SAGREDO: To też skończymy dziś na tym i pozwolimy umysłowi
uspokoić się nocnym spoczynkiem, aby jutro (jeżeli się panowie zgadzają)
powrócić do pożądanych i głównych rozważań.
SALVIATI: Nie omieszkam, o tej samej godzinie co i dziś, służyć wam i
was zadowolić.
Koniec dnia pierwszego.
DZIEŃ DRUGI
Rozważania dnia drugiego, poświęcone wyłącznie
wytrzymałości belek i zagadnieniom pokrewnym, pominięto.
Nie są wolne od błędów - nieuniknionych z uwagi na stan wiedzy w tym
zakresie w I połowie XVII w.
Poniższy spis treści rozmów Dnia
Drugiego pochodzi z polskiego wydania.
Prawo równowagi drąga -
Drąg do podważania ciężarów -
Wytrzymałość na rozciąganie i złamanie -
Wysokość i szerokość belek -
Siły, przyłożone do końców belek wmurowanych, działają proporcjonalnie
do długości belek -
Wytrzymałość proporcjonalna do sześcianu z wysokości belki i do
półtoracznej potęgi z objętości -
Wytrzymałość na złamanie graniastosłupów i walców podobnych -
Wytrzymałość na rozciąganie prętów i sznurów -
Wielkie i małe twory -
Kości olbrzymów, granice wielkości ryb -
Złamanie pod własnym ciężarem -
Zmiany położenia podpór -
Potęga geometrii i logiki -
Oznaczenie siły potrzebnej do złamania belki -
Belka o zmniejszającej się wysokości -
Belka paraboliczna wszędzie jednakowo wytrzymała -
Kwadratura paraboli -
Sposoby rysowania paraboli -
Wytrzymałość walców pustych -
Porównanie wytrzymałości walców pełnych i pustych
DZIEŃ TRZECI
O ruchu miejscowym
Poniżej pominięto większość geometrycznych dowodów
twierdzeń,
choć kilka pozostawiono, aby dać czytelniczkom/kom sposobność zapoznania
się z charakterem Galileuszowych wywodów.
Twierdzenie o tym ruchu -
Ruch naturalnie przyspieszony -
Określenie tego ruchu -
Przyczyna przyspieszenia, podtrzymywanie ręką kamienia spadającego -
Rozpowszechnione błędne poglądy -
Prędkość spadku wzdłuż równi pochyłych jednakowej wysokości, zahamowane
wahadło -
Twierdzenie I o ruchu przyspieszonym i ruchu jednostajnym, przy równości
dróg i czasów -
Twierdzenie II o proporcjonalności dróg do kwadratów z czasów -
Wniosek I. Drogi jak liczby nieparzyste -
Doświadczenia stwierdzające -
Wniosek II o stosunku czasów ruchu dwóch dróg -
Spadek po równiach pochyłych -
Prędkości osiągane przy tym spadku -
Twierdzenia III-VI o czasach spadku po równiach -
Wnioski I-III z tych twierdzeń -
Twierdzenia VII i VIII o czasach spadku po równiach i cięciwach -
Twierdzenia IX-XII o czasach spadku po równiach w różnych warunkach -
Zadania I-III o tych równiach. Twierdzenie XIII o czasach spadku po
równiach, następującego po spadku wzdłuż prostopadłej -
Zadania IV-VII o różnych kombinacjach takich spadków -
Twierdzenie XIV. Wysokość spadku po prostopadłej i droga dalszego
spadku po równi, przebyta w tym samym czasie -
Zadania VIII i IX i objaśnienia dotyczące poprzednio wymienionego
przedmiotu -
Twierdzenia XV i XVI o podnoszeniu się po równi i o ruchu poziomym,
następującym po ruchu wzdłuż równi -
Zadanie X. Podnoszenie się wzdłuż równi, następujące po spadku
prostopadłym. Twierdzenia XVII i XVIII o drogach wzdłuż różnych części
równi, przebywanych w tym samym czasie i o spadku wzdłuż dwóch cięciw -
Zadania XI. Bieg poziomy po spadku z różnych wysokości -
Twierdzenia XIX i XX. Drogi spadków w czasie najkrótszym -
Twierdzenie XXI. Najkrótsze czasy spadku wzdłuż różnych części równi
pochyłej -
Zadania XII-XIV. O ruchu poprzedzającym ruch wzdłuż równi pochyłej -
Twierdzenie XXII. Najkrócej trwający spadek po dwóch sąsiednich
cięciwach. Spadek po łuku koła -
Zadania XV i XVI. Ruch po odcinku równi i drogi poziome, przebywano po
spadku pionowym
O bardzo starym przedmiocie przynosimy naukę zupełnie nową. Nie ma nic
dawniejszego w naturze od ruchu, a pisma o nim filozofów są nieliczne i
niewystarczające. Znam liczne i godne uwagi jego objawy, dotąd nie
zaobserwowane i nie dowiedzione. Niektóre mniej ważne opisywano, jak
np. że ruch naturalny ciężaru spadającego jest stale przyspieszany. Ale
jaki jest stosunek tego przyspieszenia, nie wskazano; nikt bowiem, o
ile wiem, nie dowiódł, że drogi przebyte w czasach równych przez
ciało wychodzące ze spoczynku i spadające, mają się do siebie jak liczby
nieparzyste, następujące po jedności. Zauważono, że ciała rzucone, czyli
pociski, opisują jakąś krzywą, ale nikt nie zaznaczył, że to jest
parabola. Że tak jest, oraz wiele innych rzeczy niemniej godnych uwagi,
będzie przeze mnie dowiedzione i co ważniejsza, udostępniona zostanie
rozległa i nader ważna umiejętność, której ta praca nasza stanie się
zawiązkiem, a której tajników nie zgłębiły umysły od mojego
przezorniejsze.
Na trzy części dzieli się ta rozprawa. W pierwszej rozważamy ruch
jednostajny. W drugiej opisujemy ruch jednostajnie przyspieszony. W
trzeciej jest mowa o ruchu gwałtownym, czyli o pociskach.
O RUCHU JEDNOSTAJNYM
Ruchu jednostajnego, czyli jednakowego, jedno tylko mamy określenie,
które wyrażam jak następuje.
Określenie
Pod równym albo jednostajnym rozumiem ruch taki, gdy w
jakichkolwiek równych sobie odstępach czasu, ciała przebywają drogi
równe.
Ostrzeżenie
Do dawnego określenia (które po prostu ruch nazywa jednakowym, gdy w
równych czasach przebywane są równe drogi) dołączyliśmy przydawkę "w
jakichkolwiek", to znaczy we wszystkich równych odstępach czasu: gdyż
zdarzyć się może, że w niektórych czasach równych drogi przebyte są
równe, ale w mniejszych cząstkach tych czasów, chociaż równych sobie,
drogi przebyte nie są równe. Z przytoczonego określenia wynikają
następujące cztery aksjomaty.
Aksjomat l
W tym samym ruchu jednostajnym droga przebywana w czasie dłuższym
jest dtuźsza od przebywanej w czasie krótszym.
Aksjomat II
W tym samym ruchu jednostajnym czas ruchu po drodze dłuższej
jest dłuższy od czasu ruchu po drodze krótszej.
Aksjomat III
W czasach równych przebywana jest przy większej prędkości droga
dłuższa niż przy mniejszej.
Aksjomat IV
Prędkość, z jaką w pewnym czasie przebywaną jest droga dłuższa,
jest większa od prędkości ruchu w tymże czasie drogi krótszej.
Twierdzenie I. Podanie I
Jeżeli ciało, poruszające się jednostajnie,
przebywa dwie drogi z
jednakową prędkością, to czasy ruchu są proporcjonalne do dróg.
 Niech bowiem ciało (rys. 40) przebywa ruchem jednostajnym
z
jednakową prędkością drogi AB i BC i niech będzie DE czas potrzebny do
przebycia AB, a EF - do przebycia BC. Twierdzę, że tak się ma droga AB
do drogi BC, jak czas DE do czasu EF. Przedłużmy w obie strony linie
dróg i czasów do G, H i l, K i podzielmy AG na
dowolną liczbę dróg równych AB, i tak samo DI na takąż liczbę czasów
równych DE; z drugiej strony weźmy na CH dowolną liczbę dróg równych BC
i takąż liczbę czasów na FK równych EF. Będą więc droga BG i czas El
jednakowymi, dowolnie wybranymi, wielokrotnościami drogi BA i czasu ED, i
tak samo droga HB i czas KE takiemiż wielokrotnościami drogi CB i czasu
FE. A ponieważ DE jest czasem ruchu po AB, to czas całkowity El
odnosi się do całej drogi BG, że zaś ruch jest jednostajny, to i w
czasie El będzie tyleż części równych DE, ile jest dróg BA w całkowitej
drodze BG i tak samo znajdujemy, że KE jest czasem ruchu po HB. Wskutek zaś założenia jednostajności ruchu, gdyby GB
było równe BH, to będzie także czas IE równy czasowi EK; gdyby zaś GB
było większe lub mniejsze od BH, to także IE będzie większe lub
mniejsze od EK. Z czterech przeto rozważanych wielkości: pierwsza AB,
druga BC, trzecia DE, czwarta EF, mieszczą się pierwsza i trzecia, to
jest droga AB i czas DE, jednakową liczbę razy w drodze GB i czasie IF,
a dowiedziono, że te ostatnie są obie jednocześnie albo równe, albo
większe, albo mniejsze od czasu EK i drogi BH, a to samo odnosi się
do wielkości drugiej i czwartej. Ma się więc wielkość pierwsza do
drugiej, to jest droga AB do drogi BC, jak trzecia do czwartej, tj.
jak czas DE do czasu EF, co było do dowiedzenia.
Niech bowiem ciało (rys. 40) przebywa ruchem jednostajnym
z
jednakową prędkością drogi AB i BC i niech będzie DE czas potrzebny do
przebycia AB, a EF - do przebycia BC. Twierdzę, że tak się ma droga AB
do drogi BC, jak czas DE do czasu EF. Przedłużmy w obie strony linie
dróg i czasów do G, H i l, K i podzielmy AG na
dowolną liczbę dróg równych AB, i tak samo DI na takąż liczbę czasów
równych DE; z drugiej strony weźmy na CH dowolną liczbę dróg równych BC
i takąż liczbę czasów na FK równych EF. Będą więc droga BG i czas El
jednakowymi, dowolnie wybranymi, wielokrotnościami drogi BA i czasu ED, i
tak samo droga HB i czas KE takiemiż wielokrotnościami drogi CB i czasu
FE. A ponieważ DE jest czasem ruchu po AB, to czas całkowity El
odnosi się do całej drogi BG, że zaś ruch jest jednostajny, to i w
czasie El będzie tyleż części równych DE, ile jest dróg BA w całkowitej
drodze BG i tak samo znajdujemy, że KE jest czasem ruchu po HB. Wskutek zaś założenia jednostajności ruchu, gdyby GB
było równe BH, to będzie także czas IE równy czasowi EK; gdyby zaś GB
było większe lub mniejsze od BH, to także IE będzie większe lub
mniejsze od EK. Z czterech przeto rozważanych wielkości: pierwsza AB,
druga BC, trzecia DE, czwarta EF, mieszczą się pierwsza i trzecia, to
jest droga AB i czas DE, jednakową liczbę razy w drodze GB i czasie IF,
a dowiedziono, że te ostatnie są obie jednocześnie albo równe, albo
większe, albo mniejsze od czasu EK i drogi BH, a to samo odnosi się
do wielkości drugiej i czwartej. Ma się więc wielkość pierwsza do
drugiej, to jest droga AB do drogi BC, jak trzecia do czwartej, tj.
jak czas DE do czasu EF, co było do dowiedzenia.
Twierdzenie II. Podanie II
Jeżeli ciało w równych czasach przebywa dwie drogi, to te drogi są
proporcjonalne do prędkości. Jeżeli zaś drogi są proporcjonalne do
prędkości, to czasy są równe.
Niech będą, na poprzednim rysunku, AB, BC, drogi przebyte w
czasach równych, a mianowicie AB z prędkością DE i BC z prędkością EF.
Twierdzę, że droga AB ma się do drogi BC, jak prędkość DE do
prędkości EF; jeżeli bowiem weźmiemy, jak poprzednio, po obu stronach
dowolne wielokrotności dróg i prędkości, mianowicie GB i IE, złożone z
części AB i DE i tak samo HB i KE, złożone z części BC i EF, to w ten
sam sposób dojdziemy do wniosku, że wielokrotności GB i IE są albo
równe, albo jednakowo większe lub mniejsze od wielokrotności BH i EK; a
więc i podanie jest oczywiste.
Twierdzenie III. Podanie III
Przy nierównych prędkościach, a równych drogach, prędkości są
odwrotnie proporcjonalne do czasów.
(...)
Twierdzenie IV. Podanie IV
Jeżeli dwa ciała w ruchu jednostajnym mają nierówne prędkości,
to drogi przebyte w czasach nierównych mają się do siebie w
stosunku złożonym ze stosunku prędkości i stosunku czasów.
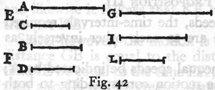 Dwa ciała (rys. 42) E i F są w ruchu jednostajnym i
stosunek prędkości ciała E do prędkości ciała F jest jak A do B; czas
zaś ruchu ciała E ma się do czasu ruchu ciała P jak C do D.
Twierdzę, że droga przebyta przez ciało E z prędkością A
w czasie C ma się do drogi przebytej przez ciało F z prędkością B
w czasie D, w stosunku złożonym ze stosunku prędkości A do prędkości B
i stosunku czasu C do czasu D. Niech będzie G droga przebyta przez
ciało E z prędkością A w czasie C i niech się ma prędkość A do prędkości
B, jak G do I, a czas C do czasu D jak l do L: wiadomo, że l jest to
droga, jaką ciało F przebywa w tym samym czasie, jak ciało E drogę G,
bo drogi G i l mają się do siebie, jak prędkości A i B: a ponieważ czas C
ma się do czasu D jak l do L, to jeżeli l jest drogą, jaką przebywa
ciało F w czasie C, będzie L drogą
przebytą przez ciało F w czasie D z prędkością B: stosunek zatem G do L
składa się ze stosunku G do I i l do L, czyli ze stosunku prędkości A do
prędkości B i czasu C do czasu D, jak to objawia podanie.
Dwa ciała (rys. 42) E i F są w ruchu jednostajnym i
stosunek prędkości ciała E do prędkości ciała F jest jak A do B; czas
zaś ruchu ciała E ma się do czasu ruchu ciała P jak C do D.
Twierdzę, że droga przebyta przez ciało E z prędkością A
w czasie C ma się do drogi przebytej przez ciało F z prędkością B
w czasie D, w stosunku złożonym ze stosunku prędkości A do prędkości B
i stosunku czasu C do czasu D. Niech będzie G droga przebyta przez
ciało E z prędkością A w czasie C i niech się ma prędkość A do prędkości
B, jak G do I, a czas C do czasu D jak l do L: wiadomo, że l jest to
droga, jaką ciało F przebywa w tym samym czasie, jak ciało E drogę G,
bo drogi G i l mają się do siebie, jak prędkości A i B: a ponieważ czas C
ma się do czasu D jak l do L, to jeżeli l jest drogą, jaką przebywa
ciało F w czasie C, będzie L drogą
przebytą przez ciało F w czasie D z prędkością B: stosunek zatem G do L
składa się ze stosunku G do I i l do L, czyli ze stosunku prędkości A do
prędkości B i czasu C do czasu D, jak to objawia podanie.
Twierdzenie V. Podanie V
Jeżeli dwa ciała poruszają się jednostajnie z nierównymi
prędkościami i drogi jakie przebywają są nierówne, to czasy ruchu
mają się do siebie jak stosunek złożony ze stosunku dróg i z odwrotnego
stosunku prędkości.
(...)
Twierdzenie VI. Podanie VI
Jeżeli dwa ciała poruszają się jednostajnie, to stosunek ich
prędkości jest równy stosunkowi złożonemu ze stosunku dróg
przebytych i odwrotnego stosunku czasów.
(...)
SALVIATI: To właśnie napisał nasz autor o ruchu jednostajnym.
Przejdziemy teraz do subtelniejszego i nowego rozważania, dotyczącego
ruchu naturalnie przyspieszonego, który się zwykle odbywa przy spadku
ciał ważkich i oto tytuł i wstęp.
O RUCHU NATURALNIE PRZYSPIESZONYM
Dotąd mówiliśmy o ruchu jednostajnym, przechodzimy teraz do ruchu
przyspieszonego. A najpierw winno być podane i objaśnione określenie
tego naturalnego zjawiska. Jakkolwiek można dowolnie wyobrazić sobie
jakikolwiek rodzaj ruchu i obserwować towarzyszące mu objawy (jak np.
ci, którzy wyobrażali sobie helisy i konchoidy, jako krzywe powstające z
pewnych ruchów, które w naturze nie mogą się zdarzać, a na zasadzie
swych przypuszczeń wywodzili chwalebnie ich własności), to jednak
postanowiliśmy rozważać te właśnie objawy, które zachodzą w naturze,
przy swobodnym spadku ciał i pozwalają godzić określenie ruchu
przyspieszonego z istotą tego ruchu w naturze.
Po długich rozmyślaniach uznaliśmy taką drogę za najlepszą, z tego
względu zwłaszcza, że to, co doświadczenie przedstawia zmysłom,
odpowiada w zupełności wyjaśnionym zjawiskom. Wreszcie do badania ruchu
naturalnie przyspieszonego doprowadziła nas, jakby ręką, uważna
obserwacja nawyków i urządzeń natury, we wszystkich jej sprawach, przy
których prowadzeniu stara się ona stosować najprostsze i najłatwiejsze
środki; bo zdaje mi się, że nikt nie będzie utrzymywał, aby pływanie lub
fruwanie mogło być wykonywane prościej i łatwiej, niż tymi środkami,
których używają naturalnym instynktem ryby i ptaki. Jeżeli przy tym
zauważę, że kamień, wychodzący ze spoczynku i spadający ze znacznej
wysokości, doznaje wciąż nowych przyrostów prędkości, to dlaczegóż nie
mam wierzyć, że te przyrosty powstają w sposób najprostszy i dla każdego
zrozumiały. Bo, badając ściśle, nie znajdziemy żadnego dodatku lub
przyrostu prostszego niż taki, który dochodzi wciąż jednakowo.
Zrozumiemy to łatwo, rozpatrując bliskie pokrewieństwo pojęć czasu i
ruchu: jak bowiem ruch jednostajny określa równość przestrzeni
przebytych w równych czasach (bo nazwaliśmy jednostajnym taki ruch,
w którym w czasach równych przebywane są drogi równe), to przy takiej
równości czasów prościej pojąć możemy wzrosty prędkości: przyjmując w
myśli ruch ten jako jednostajny i w jednakowy sposób stale
przyspieszany, bo w jakichkolwiek czasach równych dochodzą równe
dodatki prędkości. Tak że, jeżeli od chwili, gdy ciało wychodzi ze
spoczynku i zaczyna spadać, weźmiemy pod uwagę równe odstępy czasu
spadania, to stopień prędkości, nabyty w ciągu pierwszego i drugiego
odstępu, będzie dwa razy większy od nabytego w ciągu samego pierwszego,
nabyty w ciągu trzech odstępów, trzy razy, a w ciągu czterech, cztery
razy większy. Tak że (dla łatwiejszego zrozumienia) gdyby ciało swój
ruch, po pierwszym odstępie czasu, z osiągniętyin stopniem albo momentem
prędkości w ten sam sposób dalej prowadziło, to poruszałoby się dwa
razy wolniej, niż gdyby stopień prędkości osiągnięty był w dwóch
odstępach czasu: nie zbłądzimy więc, jeżeli przyjmiemy, że natężenie
prędkości odpowiada przeciągowi czasu: skąd wynika takie określenie
ruchu, którym się mamy zajmować: Równomiernie, albo jednostajnie
przyspieszonym nazywamy taki ruch, który, od chwili wyjścia ze
spoczynku, w czasach równych, przydaje sobie równe momenty prędkości.
SAGREDO: Nie będę się sprzeciwiał tej lub każdej innej definicji,
postawionej przez jakiegoś autora, bo wszystkie one są arbitralne: mogę
wszakże, nie obrażając nikogo, powątpiewać, czy takie abstrakcyjnie
zupełnie postawione definicje nadają się i sprawdzają, dla tego rodzaju
ruchu przyśpieszonego, jaki wykonują ciała ważkie naturalnie spadające.
A ponieważ zdaje się, że nasz autor zapewnia, że to, co określa jest
naturalnym ruchem ciał ważkich, pragnąłbym chętnie, aby mi odjęto pewne
skrupuły, które mnie bałamucą; abym mógł potem z tym większą uwagą
wysłuchać dowodzeń, na które czekamy.
SALVIATI: Zechciejcie więc, Waszmość i pan Simplicio, przystąpić do
formułowania zarzutów. Wyobrażam sobie, że będą te same, jak te, które
sobie przypominam, gdy pierwszy raz zobaczyłem tę rozprawę i które w
części odparte zostały przez samego autora, a w części po własnem
zastanowieniu się odrzucone.
SAGREDO: Weźmy pod uwagę ciało ważkie wychodzące ze spoczynku, czyli
ze stanu, w którym pozbawione było wszelkiej prędkości, i rozpoczynające
ruch w ten sposób, że jego prędkość, od pierwszej chwili, rośnie
proporcjonalnie do czasu: tak że, jeżeli w ciągu ośmiu uderzeń pulsu
nabywa osiem stopni prędkości, to przy czwartem uderzeniu ma ich tylko
cztery, przy drugim dwa, a przy pierwszym jeden, a ponieważ czas jest
nieskończenie podzielny, wynika stąd że, jeżeli poprzedzające
prędkości mają być mniejsze w tym samym stosunku, to nie można wyobrazić
sobie tak małej prędkości, z jakąby ciało musiało się poruszać w chwili
nieskończonej powolności, tj. gdy wychodziło ze spoczynku. Jeżeliby więc
ciało, z prędkością osiągniętą w ciągu czterech uderzeń pulsu i
pozostającą bez zmiany, przebywało dwie mile w ciągu godziny, a z
osiągniętą w ciągu dwóch uderzeń pulsu - jedną milę, to twierdzić
należy, że w chwilach najbliżej sąsiadujących z wyjściem ze stanu
spoczynku, ruch ciała będzie tak powolny, że (przy dalszym równie
powolnym ruchu) ciało nie przebiegnie jednej mili ani w ciągu godziny,
ani w ciągu dnia, roku i tysiąca lat i w ciągu jeszcze dłuższego czasu
nie posunie się ani na palec: zjawisko, które trudno nam śledzić
wyobraźnią, bo zmysły nasze pokazują nam, że ciało ważkie spada nagle z
wielką prędkością.
SALVIATI: Ta sama trudność zajmowała mnie
na początku, ale ją wnet przezwyciężyłem: a udało mi się to przez
takie doświadczenie, jak to, które co dopiero było przytoczone.
Powiedzieliście, że doświadczenie wskazuje, iż ciało skoro tylko
wychodzi że spoczynku ma zaraz znaczną prędkość; a ja powiadam, że to
samo doświadczenie wyjaśnia, że pierwszy impet bardzo nawet ciężkiego
ciała jest powolny i opóźniony. Połóżcie ciężar na masie miękkiej, to
ustępuje pod ciśnieniem, jakie wywiera ciężar; oczywiście więc, jeżeli
podniesiemy ciężar na łokieć lub dwa i spuścimy go, aby spadł na tę
samą masę, to przy uderzeniu wywarte będzie nowe i większe ciśnienie
aniżeli to, które przedtem wywarł sam ciężar; skutek wywarty będzie
wtedy przez ciało spadające i przez prędkość nabytą podczas spadku, a
ten skutek będzie tym większy, im z większej wysokości nastąpi
uderzenie, to jest im większą będzie prędkość ciała uderzającego. Jaka
zaś jest prędkość spadającego ciężaru, o tej możemy bez błędu
wnioskować ze sposobu i wielkości uderzenia. Ale powiedzcie mi mości
panowie, jeżeli na pal spuszczamy babę kafara z wysokości czterech łokci
i ta wbija go w ziemię np. na cztery
palce, to spuszczona z dwóch łokci wbije go mniej, a z jednego jeszcze
mniej, i jeszcze mniej z wysokości piędzi; a, jeżeli w końcu podniesioną
będzie tylko na palec, to, czy nie zdziała tyle, jakby była położoną bez
uderzenia? z pewnością bardzo mało i działanie byłoby zupełnie
niedostrzegalne, gdyby była podnoszona tylko na taką wysokość, jak gruby
jest papier. A ponieważ skutek uderzenia zależy od prędkości ciała uderzającego, to któżby mógł wątpić, że gdy ruch jest
bardzo wolny, a prędkość jak najmniejsza, to jej działanie jest
niedostrzegalne? Uwydatnia się tu potęga prawdy, bo to samo
doświadczenie, które na pierwszy rzut oka zdawało się dowodzić pewnej
rzeczy, lepiej rozważane wykazuje rzecz wprost przeciwną. Ale nawet bez
uciekania się do takiego doświadczenia (które bez wątpienia jest
jak najwięcej przekonujące), zdaje mi się, że nie trudno będzie
przeniknąć do prawdy prostym rozumowaniem. Mamy ciężki kamień,
podtrzymywany w powietrzu w spoczynku: jeżeli odejmiemy podporę i damy mu swobodę,
to, będąc cięższym od powietrza, spada na dół i to nie ruchem
jednostajnym, lecz z początku powolnym a następnie stale
przyspieszonym; a że prędkość może się powiększać lub zmniejszać bez
granic, to cóż by przekonać mnie mogło, że takie ciało, wychodząc z
nieskończenie wielkiej powolności (gdyż tym jest spoczynek), przyjmie
od razu raczej dziesięć stopni prędkości, a nie cztery, dwa, jeden, pól
lub jedną setną stopnia? lub zresztą wszystkie mniejsze, do
nieskończoności? Zechciejcie to przyznać. Nie przypuszczam, abyście
odmawiali swej zgody na to, że osiąganie stopni prędkości przez kamień
spadający, od chwdi wyjścia ze spoczynku, następuje w tym samym
porządku, jak zmniejszanie się lub strata tychże stopni przy podrzucaniu
go siłą popychającą w górę, do tej samej wysokości: a jeżeli tak jest,
to wydaje mi się niewątpliwe, że przy zmniejszaniu się prędkości
podnoszącego się kamienia, gdy ta w końcu zostaje unicestwiona, kamień
nie prędzej dojdzie do stanu spoczynku, póki nie przejdzie przez
wszystkie stopnie powolności.
SIMPLICIO: Ale skoro stopnie coraz większej powolności są w liczbie
nieskończonej, to nigdy nie będą wszystkie wyczerpane; a więc podnoszące się ciało ważkie nigdy nie dojdzie do spoczynku,
ale poruszać się będzie nieskończenie, ciągle się opóźniając: czego nie widać, aby się zdarzało.
SALVIATI: Zdarzałoby się to, panie Simplicio, gdyby ciało z
każdym stopniem prędkości poruszało się przez czas pewien; ale ono
przez każdy taki stopień przechodzi, nie trwając w nim ani chwilę a w
każdym najmniejszym przeciągu czasu jest takich chwil nieskończenie
wiele, wystarczają one przeto, aby odpowiadać nieskończenie wielu
stopniom zmniejszającej się prędkości. Że zaś ciało, lecące w górę, nie
utrzymuje się w ciągu żadnego przeciągu czasu w tym samym stopniu
prędkości, to można w ten sposób wykazać: jeżeli określony zostanie pewien przeciąg czasu, to miałoby ciało w
pierwszej chwili tego okresu, jak i w ostatniej, ten sam stopień
prędkości, i w tym samym stopniu utrzymywałoby się w ciągu następnego
okresu na przebywanej przestrzeni i jak przechodziło od pierwszego
okresu do drugiego, dla tej samej przyczyny przeszłoby tak samo od
drugiego do trzeciego, aż w końcu utrzymałoby się do nieskończoności w
ruchu jednostajnym.
SAGREDO: Z rozważania tego wyciągnąć by można dość trafne rozwiązanie
poruszanej przez filozofów kwestil, jaka jest przyczyna przyspieszenia
w ruchu naturalnym ciał ważkich. Bo, jak uważam, przy ruchu ciężaru
rzuconego pod górę, siła (virtu) rzutu wciąż się zmniejsza i dopókąd się
nie zrówna z przeciwdziałającą ciężkością, to ciężar się podnosi, a gdy
się siła i ciężkość zrównoważą, to ciężar przestaje się podnosić i
przechodzi w stan spoczynku, w którym popęd, jaki mu był udzielony, nie
inaczej zostaje unicestwiony, jak tylko przez to, że zużytą została
przewyżka, jaką miał poprzednio nad ciężarem ciała, dzięki której ciało
mogło się podnosić do góry. Gdy więc trwa zmniejszanie się tego obcego
popędu i następuje przewyżka ciężaru ciała, wtedy zaczyna się spadanie,
ale bardzo powolne, wskutek przeciwdziałania nadanego popędu, którego
znaczna część jeszcze się w ciele utrzymuje; a ponieważ ten popęd wciąż
się zmniejsza i ciężkość wciąż w większym stosunku przeważa, powstaje
stąd stałe przyspieszenie ruchu.
SIMPLICIO: Pomysł jest dowcipny, ale raczej pięknie obmyślany niż
trafny. Gdyż to, co się w nim wydaje zadowalające, odnosi się tylko do
ruchu naturalnego, poprzedzonego ruchem gwałtownym, przy czym utrzymuje
się w nim jeszcze część udzielonego popędu, który dał początek ruchowi
gwałtownemu: lecz gdy nie ma żadnej takiej pozostałości i ciało po
długotrwałym spoczynku puszcza się w ruch, to całe rozumowanie traci
swą silę.
SAGREDO: Sądzę że jesteście w błędzie i że to odróżnianie przypadków
jest zbyteczne albo, lepiej mówiąc, żadne. Bo powiedzcie mi, czyliż
przy podrzucaniu nie może być nadany ciału popęd, raz wielki, raz mały,
tak że ciało wznieść się może na wysokość stu łokci, albo dwudziestu,
albo czterech, albo jednego?
SIMPLICIO: Tak, bezwątpienia.
SAGREDO: I nie mniej udzielony popęd może tak mało przewyższać opór
ciężkości, że ciało podniesie się tylko na szerokość palca; a w końcu
popęd może być tylko taki, że będzie równoważył opór ciężkości tak, że
ciało nie będzie podniesione w górę a tylko podtrzymane. Gdy więc
trzymacie w ręku kamień, czyż robicie co innego, jak to, ze mu nadajecie
taki popęd do podnoszenia się w górę,
jaka jest jego ciężkość pociągająca go w dół? l czy nie nadajecie mu
tego popędu przez cały czas trzymania w ręku? Czy może ten popęd się
zmniejsza w ciągu długiego trzymania? A czyż to ma jakieś znaczenie, że
tą podporą, nie dopuszczającą, aby kamień spadał, jest nasza ręka, lub
stół, albo sznur, na którym jest zawieszony? Oczywiście nie. Wynika więc
stąd, panie Simplicio, że, czy dłuższy czy krótszy czas, albo tylko
chwila spoczynku poprzedza spadek kamienia, nie czyni to żadnej
różnicy, bo kamień się nie ruszy, dopókąd działa popęd przeciwny jego
ciężkości, a ściśle wystarczający do utrzymania go w spoczynku.
SALVIATI: Nie wydaje mi się odpowiednim rozpoczynanie obecnie
badania przyczyny przyspieszenia ruchu naturalnego, o czem różni
filozofowie różne wyrazili poglądy: jedni odnosili to do zbliżania się
do środka, inni do tego, że wciąż mniej części chce się od siebie
oderwać, inni znów do oporu otaczającego ośrodka, który schodzi się za ciałem spadającem, popychając je i wciąż goniąc; wszystkie te zapatrywania, wraz z innymi podobnymi poddać by należało
sprawdzeniu i rozpatrzeniu, choć się mało na tym zyska. Na teraz
wystarczy naszemu autorowi, abyśmy zrozumieli, jak on badać i objaśniać
zamierza niektóre własności ruchu przyspieszonego (jakakolwiek byłaby
ich przyczyna), równie jak momenty prędkości, od wyjścia ciała ze
spoczynku, wciąż rosnące w najprostszym stosunku do wzrostu czasu
trwania ruchu, co znaczy, że w równycb czasach następują równe przyrosty
prędkości. A gdy się okaże, że przypadki, które zostaną przedstawione,
sprawdzają się przy naturalnym ruchu ciała spadającego z
przyspieszeniem, to będziemy mogli przyjąć, że powyższe określenie
odnosi się do takiego ruchu ciężarów i że prawdą jest, że przyspieszenie
jest proporcjonalne do czasu trwania ruchu.
SAGREDO: O ile teraz rozumiem, to zdaje mi się, że bez zmiany
pomysłu tak można to wyraźniej określić: Ruch jednostajnie
przyspieszony jest taki, przy którym prędkość wzrasta proporcjonalnie
do przebytej drogi: tak że np. przy spadku z wysokości czterech łokci,
prędkość jest dwa razv większa, niż przy spadku z wysokości dwóch łokci,
a ta znów dwa razy od odpowiadającej wysokości jednego łokcia. Wydaje mi
się bowiem niewątpliwe, że ciało spadające z wysokości sześciu łokci
uderza z impetem dwa razy większym, niż gdy spada z wysokości trzech
łokci, a trzy razy większym w porównaniu ze spadkiem z dwóch łokci, i
sześć razy większym niż przy spadku z wysokości jednego łokcia.
SALVIATI: Pociesza mnie to,
że miałem takiego towarzysza w błędzie; powiem Wam nadto, że Wasze przedstawienie ma w sobie tyle
prawdopodobieństwa, że sam nasz autor mi nie przeczył, gdy mu je
komunikowałem i że on przez pewien czas pozostawał w tym samym błędzie.
Co wszakże najwięcej podziwiałem, to gdy ujrzałem, jak w czterech
najprostszych słowach objawiają się nie tyle fałszywe ile niemożliwe dwa
podania, które uważałem dopiero co za prawdopodobne i wielu je
przedstawiałem, nie znalazłszy takich, którzy by się na nie nie
zgadzali.
SIMPLICIO: Ja także stanąłbym w rzędzie zgadzających się: a
że ciało spadające nabywa sił w spadku, gdy prędkość rośnie
proporcjonalnie do drogi przebytej i moment jego uderzenia jest
podwójny przy dwa razy większej wysokości, to do tych podań można się
przyłączyć bez wstrętu i przeciwu.
SALVIATI: A jednak są one równie fałszywe i niemożliwe jak to,
że ruch odbywa się momentalnie. l oto najjaśniejsze dowodzenie. Gdyby
prędkości były proporcjonalne do dróg przebytych lub mających być
przebytymi, to by te drogi przebywane były w czasach równych; skoro
więc prędkość, z jaką ciało spadające przebywa cztery łokcie, miałaby
być dwa razy większa od prędkości ruchu dwóch pierwszych łokci, to
musiałyby czasy tych dwóch przebiegów być sobie równe; ale przebieg
przez to samo ciało czterech łokci w tym samym czasie co i dwóch łokci,
możliwy jest tylko przy ruchu momentalnym, a my widzimy, że ciało
spadające dokonuje swego ruchu w czasie i w mniejszym przeciągu czasu
przebywa dwa łokcie aniżeli cztery; fałszem więc jest, aby prędkość
ciała spadającego wzrastała tak, jak przebyta droga. Dowieść można z
równą jasnością, że i drugie podanie jest błędne. Bo ponieważ ciało
uderzające jest to samo, różnica i moment uderzeń określane są tylko
różnicą prędkości. Gdyby ciało spadające z podwójnej wysokości
wytwarzało podwójny moment uderzenia, to musiałoby uderzać z podwójną
prędkością; ale z podwójną prędkością ciało przebywałoby w tym samym
czasie podwójną drogę, a my widzimy, że czas spadku z większej wysokości
jest dłuższy.
SAGREDO: Z nadzwyczajną jasnością i łatwością objawiacie nam
ukryte wnioski; ta wielka łatwość czyni je mniej cennymi, niż gdy bywały
stawiane wobec prawdopodobieństwa sprzeciwu. Myślę, że mniej ceniłbym
ogólne wiadomości, nabyte z tak małym trudem, w porównaniu z tymi, co do
których prowadzono długie a niepojęte rozprawy.
SALVIATI: Byłoby to jeszcze znośne, gdyby ci, którzy krótko i jasno
wykazują błędy podań, poczytywanych ogólnie za prawdziwe, otrzymywali
tylko pogardę zamiast uznania; ale więcej jeszcze nieprzyjemnego i
przykrego wrażenia doznają ci, którzy w tym samym dziale wiedzy starając
się dorównać każdemu, dowiadują się potem, że pominęli prawdziwe wnioski,
które przez innego krótką i łatwą rozprawą zostały wykryte i wykazane
jako błędne. Nie nazwę tego uczucia zazdrością, zamieniającą się zwykle
w gniew i nienawiść do odkrywców takich błędów, ale powiem, że jest to
pobudką albo pożądaniem, aby raczej trzymać się zastarzałych błędów,
aniżeli pozwalać na przyjęcie nowo odkrytej prawdy, które to pożądanie
prowadzi nieraz do stawiania sprzeciwu prawdzie przez siebie
podzielanej, dlatego tylko, aby się skłonić do poglądu licznego a mało
inteligentnego tłumu innej opinii. O takich fałszywych wnioskach,
przyjmowanych za prawdziwe i o łatwych sprzeciwach, często słyszałem
mówiącego naszego akademika, i dobrze to zapamiętałem.
SAGREDO: Nie powinna nas Waszmość tego pozbawiać, ale przy
sposobności nam zakomunikować, nawet, gdyby trzeba było poświęcić temu
osobne posiedzenie. Tymczasem, ciągnąc dalej nasze rozprawy, ustalające
określenie ruchu jednostajnie przyspieszonego, dochodzimy do
następującego:
Ruchem równomiernie albo jednostajnie przyspieszonym nazywamy ruch
taki, przy którym, od wyjścia ze spoczynku, w czasach równych, dochodzą
równe momenty prędkości.
SALVIATI: Po ustaleniu tego określenia, stawia nasz autor i przyjmuje
za prawdziwą taką zasadę:
Przyjmuję, że stopnie prędkości nabyte przez toż samo ciało, przy
różnych nachyleniach równi pochyłych, są sobie równe, skoro wysokości
tych równi są równe.
Wysokością równi pochyłej nazywa prostopadłą, spuszczoną z
najwyższego punktu tej równi na linią poziomą, przechodzącą przez
najniższy punkt tejże równi pochyłej, jeżeli więc (rys. 44) BA
jest równoległa do poziomu, nad którą wznoszą się równie pochyłe CA,
CD, to będzie prostopadła CB, spuszczona na poziomą BA, nazwana przez
autora wysokością równi CA, CD i przyjmuje on, że stopnie prędkości
tegoż samego ciała, spadającego wzdłuż równi pochyłych CA, CD, nabyte w
punktach końcowych A, D, są jednakowe, bo ta sama jest wysokość obu
równi CB. I takiż sam jeszcze stopień prędkości miałoby ciało spadające
z punktu C, przy końcu spadku w B.
SAGREDO: Istostnie, przypuszczenie to ma, o ile mi się zdaje, tyle
prawdopodobieństwa, że zasługuje na przyjęcie bez sprzeciwu, zakładając
zawsze, że usunięte zostaną wszystkie przypadkowe, zewnętrzne
przeszkody i że równie są twarde i gładkie, a ciało m kształt doskonale
okrągły, tak że i ciało i równia nie mają chropowatości. Gdy wszystkie
te sprzeczności i przeszkody są usunięte, mówi mi zdrowy rozsądek bez
trudności, że ciężka i doskonale okrągła kula schodząca po liniach CA,
CD, CB, dochodziłaby do spodów A, D, B z jednakowymi impetami.
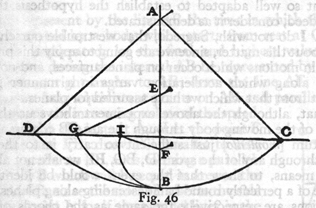 SALVIATI: Rozumujecie bardzo prawdopodobnie, lecz
oprócz tego pragnę Warn przez jedno doświadczenie tak jeszcze wzmocnić
to prawdopodobieństwo, abyście je mogli przyrównać do wystarczającego
dowodzenia. Niech Wam ten papier przedstawia na poziomej płaszczyźnie
wystawioną ścianę, na wbitym w nią gwoździu wisi kula ołowiana, jedno
lub dwuuncjowa (rys. 46) zawieszona na cienkiej nici AB, dwa
do trzech łokci długiej, prostopadle do poziomu; na ścianie narysujemy
poziomą DC, przecinającą pod kątem prostym pionową AB, która na
szerokość dwóch palców jest oddalona od ściany; jeżeli nić AB z kulą
odchylimy do AC i puścimy kulę swobodnie, to zobaczymy, że ta spadając
opisze łuk CBD, przeleci przez jego spód B i biegnąc po BD podniesie się
prawie do narysowanej poziomej CD, nie dochodząc do niej tylko na
bardzo a bardzo małą odległość, wskutek oporu powietrza i nici. Stąd
możemy prawdziwie wnioskować, ze impet nabyty w punkcie B przez kulę,
przy spadaniu po łuku CB, wystarcza, aby ją podnieść po łuku BD do tej
samej wysokości; po zrobieniu i kilkakrotnym powtórzenie tego
doświadczenia, jeżeli gwóźdź wbijamy na kierunku AB w E albo w F, tak
aby sterczał na pięć lub sześć palców; to ten zatrzyma nić AC posuwającą
się przy ruchu kuli po łuku CB i wbity w E zmusi kulę do ruchu po
łuku BG, opisanym ze środka E, skąd widzimy, czego dokonać może ten sam
impet, który przedtem, poczynając od tegoż samego punktu B, podnosił
to samo ciało po łuku BD do wysokości poziomej CD. Teraz panowie
zauważcie dobrze, że kula dochodzi do linii poziomej w punkcie G i to
samo następuje, gdy przeszkodę umieścimy niżej, np. w F,
wtedy kula opisze łuk BI, kończąc zawsze swe podnoszenie się dokładnie
na linii CD; a gdyby gwóźdź przeszkadzający wbity był tak nisko, że
reszta nici nie wystarczałaby do dosięgnięcia poziomu CD (co
nastąpiłoby, gdyby gwóźdź był bliższy B niż punktu przecięcia AB z
poziomą CD), to nić nawinęłaby się na gwóźdź. Doświadczenie to nie
pozwala powątpiewać o prawdziwości przypuszczenia: bo ponieważ łuki CD i
DB są równe i podobnie położone, więc nabytek momentu przy spadaniu po
łuku CB jest ten sam, jak przy spadaniu po łuku DB; ale moment nabyty w
B, na łuku CB, wystarcza do podniesienia tegoż samego ciała po łuku BD;
więc i moment nabyty przy spadaniu po DB jest równy momentowi, który to
samo ciało podnosi po tym samym łuku od B do D, tak że w ogóle każdy
moment, osiągnięty przy spadku, jest równy temu, który może podnieść to
samo ciało po tym samym łuku: ale
wszystkie momenty, które mogą podnosić ciało po łukach BD, BG, BI, są
sobie równe, bo są nabyte przez to samo ciało przy spadaniu po łuku CB,
jak wykazało doświadczenie: a więc i wszystkie momenty, nabyte przy
spadaniu po łukach DB, GB, IB, są sobie równe.
SALVIATI: Rozumujecie bardzo prawdopodobnie, lecz
oprócz tego pragnę Warn przez jedno doświadczenie tak jeszcze wzmocnić
to prawdopodobieństwo, abyście je mogli przyrównać do wystarczającego
dowodzenia. Niech Wam ten papier przedstawia na poziomej płaszczyźnie
wystawioną ścianę, na wbitym w nią gwoździu wisi kula ołowiana, jedno
lub dwuuncjowa (rys. 46) zawieszona na cienkiej nici AB, dwa
do trzech łokci długiej, prostopadle do poziomu; na ścianie narysujemy
poziomą DC, przecinającą pod kątem prostym pionową AB, która na
szerokość dwóch palców jest oddalona od ściany; jeżeli nić AB z kulą
odchylimy do AC i puścimy kulę swobodnie, to zobaczymy, że ta spadając
opisze łuk CBD, przeleci przez jego spód B i biegnąc po BD podniesie się
prawie do narysowanej poziomej CD, nie dochodząc do niej tylko na
bardzo a bardzo małą odległość, wskutek oporu powietrza i nici. Stąd
możemy prawdziwie wnioskować, ze impet nabyty w punkcie B przez kulę,
przy spadaniu po łuku CB, wystarcza, aby ją podnieść po łuku BD do tej
samej wysokości; po zrobieniu i kilkakrotnym powtórzenie tego
doświadczenia, jeżeli gwóźdź wbijamy na kierunku AB w E albo w F, tak
aby sterczał na pięć lub sześć palców; to ten zatrzyma nić AC posuwającą
się przy ruchu kuli po łuku CB i wbity w E zmusi kulę do ruchu po
łuku BG, opisanym ze środka E, skąd widzimy, czego dokonać może ten sam
impet, który przedtem, poczynając od tegoż samego punktu B, podnosił
to samo ciało po łuku BD do wysokości poziomej CD. Teraz panowie
zauważcie dobrze, że kula dochodzi do linii poziomej w punkcie G i to
samo następuje, gdy przeszkodę umieścimy niżej, np. w F,
wtedy kula opisze łuk BI, kończąc zawsze swe podnoszenie się dokładnie
na linii CD; a gdyby gwóźdź przeszkadzający wbity był tak nisko, że
reszta nici nie wystarczałaby do dosięgnięcia poziomu CD (co
nastąpiłoby, gdyby gwóźdź był bliższy B niż punktu przecięcia AB z
poziomą CD), to nić nawinęłaby się na gwóźdź. Doświadczenie to nie
pozwala powątpiewać o prawdziwości przypuszczenia: bo ponieważ łuki CD i
DB są równe i podobnie położone, więc nabytek momentu przy spadaniu po
łuku CB jest ten sam, jak przy spadaniu po łuku DB; ale moment nabyty w
B, na łuku CB, wystarcza do podniesienia tegoż samego ciała po łuku BD;
więc i moment nabyty przy spadaniu po DB jest równy momentowi, który to
samo ciało podnosi po tym samym łuku od B do D, tak że w ogóle każdy
moment, osiągnięty przy spadku, jest równy temu, który może podnieść to
samo ciało po tym samym łuku: ale
wszystkie momenty, które mogą podnosić ciało po łukach BD, BG, BI, są
sobie równe, bo są nabyte przez to samo ciało przy spadaniu po łuku CB,
jak wykazało doświadczenie: a więc i wszystkie momenty, nabyte przy
spadaniu po łukach DB, GB, IB, są sobie równe.
SAGREDO: Rozumowanie wydaje mi się tak ścisłe, a doświadczenie tak
przystosowane do sprawdzenia postulatu, że ten postulat uważać można
za dowiedziony.
SALVIATI: Ja sądzę, panie Sagredo, że nie potrzebujemy troszczyć się
o to, że twierdzenie nasze stosować będziemy do ruchów po powierzchniach
prostych a nie po krzywych, na których przyspieszenie inaczej się
powiększa, aniżeli to przyjmujemy na płaszczyznach prostych. Gdy więc
doświadczenie nas uczy, że spadanie ciała po łuku CB daje mu taki
moment, że może się podnosić po którymkolwiek z łuków BD, BG, Bl, to nie
możemy z równą widocznością wykazać, że to samo nastąpi, gdy zupełnie
doskonała kula spada po płaszczyznach prostych, nachylonych tak samo
jak cięciwy tych łuków; prawdopodobne jest raczej, że gdy utworzone
będą kąty z tych płaszczyzn prostych w punkcie B, to kula spadająca po
pochyłości wzdłuż cięciwy CB, doznając przeszkody na płaszczyznach
podnoszących się wzdłuż cięciw BD, BG, Bl, przez uderzenia o nie,
straciłaby na swoim impecie i nie mogłaby, podnosząc się, dojść do
wzniesienia linii CD. Ale po usunięciu przeszkody, co przesądza
doświadczenie, wydaje mi się zupełnie zrozumiałe, że impet (pochodzący
istotnie od siły ilości spadku) starczyć powinien do doprowadzenia ciała
do tej samej wysokości. Przyjmijmy to więc tymczasem za postulat, którego
prawda absolutna później zostanie ustalona, gdy zobaczymy inne wnioski
wynikające z tej hypotezy i sprawdzimy je ściśle doświadczeniem. Po
postawieniu tej jednej zasady, przechodzi autor do twierdzeń ściśle
dowodzonych, z których pierwsze jest następujące:
Twierdzenie I. Podanie I

Czas, w którym jakąkolwiek drogę przebywa
ciało wychodzące ze
spoczynku i poruszające się ruchem jednostajnie przyspieszonym, jest
równy czasowi, w którym by ta sama droga przebyta została przez to samo
ciało, biegnące ruchem jednostajnym, którego stopień
prędkości jest połową ostatniego i największego stopnia prędkości ruchu
przyspieszonego.
Niech AB (rys. 47) przedstawia czas, w którym ciało,
wychodzące ze spoczynku w C, przebywa ruchem jednostajnie przyspieszonym
drogę CD; a stopień prędkości powiększający się na poszczególnych
odstępach czasu AB, ostatni największy niech będzie EB, na prostopadłej
do AB; poprowadźmy AE oraz wszystkie do EB równoległe i jednakowo od
siebie odległe linie, to będą one przedstawiały rosnące stopnie
prędkości, poczynając od A. Przepołówmy EB w F, poprowadźmy FG, AG,
równoległe do AB, FB, prostokąt AGFB będzie równy trójkątowi AEB, bo GF
przepoławia linię AE w punkcie I: a jeżeli równoległe w trójkącie AEB
przedłużone zostaną do GIF, to będzie suma wszystkich równoległych
zawartych w czworokącie równa sumie
zawartych w trójkącie AEB; bo te, co są w trójkącie IEF, są równe tym,
które się mieszczą w trójkącie GIA; podczas gdy zawarte w trapezie AlFB
są wspólne. A że każdemu z odstępów czasu w AB odpowiada jedna linia i
wszystkie punkty AB, przez które w trójkącie AEB poprowadzone zostały
równoległe, przedstawiają rosnące stopnie prędkości, podczas gdy linie
równoległe w prostąkocie wyobrażają taką samą liczbę tegoż samego
stopnia prędkości jednostajnej, to jasne jest, że wszystkie momenty
prędkości przy ruchu przyspieszonym przedstawione są przez rosnące
równoległe w trójkącie AEB, a przy ruchu jednostajnym przez równe linie
równoległe prostokąta GB: czego bowiem braknie momentom w pierwszej
połowie ruchu przyspieszonego (braknie równoległych zawartych w
trójkącie AGI), to przybywa momentom przez równoległe w IEF. A więc dwa
ciała przebędą równe drogi w tym samym czasie, jedno biegnąc od
początku ruchem jednostajnie przyspieszonym, a drugie ruchem jednostajnym
ze stałą prędkością równą połowie największej prędkości nabytej w ruchu
przyspieszonym, czego należało dowieść.
Twierdzenie II. Podanie II
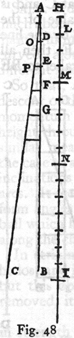 Jeżeli ciało, wychodząc ze spoczynku, spada ruchem jednostajnie
przyspieszonym, to drogi przebyte w jakichkolwiek czasach są do siebie
w podwójnym stosunku czasów, tj. w stosunku kwadratów z czasów.
Jeżeli ciało, wychodząc ze spoczynku, spada ruchem jednostajnie
przyspieszonym, to drogi przebyte w jakichkolwiek czasach są do siebie
w podwójnym stosunku czasów, tj. w stosunku kwadratów z czasów.
Niech długość (rys. 48) AB przedstawia czas upływający od
pewnej chwili początkowej A, zawierając w sobie dwa jakiekolwiek czasy
AD, AE; niech będzie także HI linia, po której ciało, wyszedłszy ze
spoczynku w H, spada ruchem jednostajnie przyspieszonym; niech będzie
dalej HL, droga przebyta w pierwszym odstępie czasu AD i HM takaż droga,
po której spadek następuje w czasie AE. Twierdzę, że stosunek drogi MH
do drogi HL jest równy podwójnemu stosunkowi czasu EA do czasu AD.
Innymi słowy drogi MH, HL są do siebie w tym samym stosunku jak kwadraty
z EA i AD. Poprowadźmy AC linię nachyloną pod jakimkolwiek kątem do AB,
przez punkty D, E, poprowadźmy równoległe DO i EP, z których DO
przedstawia maksimum stopnia prędkości nabytej w chwili D czasu AD, a PE
takież maksimum stopnia prędkości nabytej w chwili E czasu AE. Ponieważ
wyżej dowiedziono, że drogi przebyte ruchem jednostajnie
przyspieszonym i ruchem jednostajnym o prędkości równej połowie
największej prędkości nabytej w ruchu przyspieszonym są równe, - wynika
stąd, że drogi MH i LH są takie, jak gdyby były przebyte ruchem
jednostajnym z prędkościami 1/2 PE i 1/2
OD w czasach EA i DA. Gdyby teraz można było wykazać, że te drogi MH l
LH mają się do siebie w podwójnym stosunku czasów EA i DA, to
twierdzenie byłoby dowiedzione. Ale w czwartym twierdzeniu pierwszej
księgi dowiedziono, że przy ruchu jednostajnym drogi przebyte mają
się do siebie w stosunku złożonym ze stosunku prędkości i stosunku
czasów: tu zaś stosunek prędkości jest taki sam jak stosunek czasów (bo
1/2
PE tak się ma do 1/2 OD, jak PE do OD a więc
tak, jak AE do AD), zatem stosunek dróg przebytych jest podwójnym
stosunkiem czasów, co było do dowodzenia.
Objaśnia to, że tenże stosunek dróg przebytych jest podwójnym
stosunkiem najwyższych stopni prędkości, to jest linii PE i OD, bo tak
się ma PE do OD, jak EA do DA.
Wniosek I
Wynika stąd, że jeżeli od początku ruchu wzięte będą następujące po
sobie równe wielkości czasów, jak AD, DE, EF, FG, w ciągu których
przebyte będą drogi HL, LM, MN, NI, to te drogi mieć się będą do
siebie jak liczby nieparzyste, poczynając od jednosci, czyli jak
1, 3, 5, 7. Bo taki jest stosunek różnic kwadratów z linii, rosnących o
jednakową długość i których przyrosty są równe najmniejszej z tych
linii: innymi stówy różnic kwadratów z liczb po sobie idących od
jedności. Gdy wiec stopnie prędkości rosną w czasach równych w prostym
szeregu liczb, to drogi przebyte w tych czasach rosną w szeregu liczb
nieparzystych, poczynając od jedności.
(...)
SIMPLICIO: Istotnie więcej mi się podoba proste i jasne
przedstawienie pana Sagredo, niż nieco ciemne dla mnie dowodzenie
Autora; tak że jestem dość mocno przekonany, że taki winien być przebieg
sprawy, jeżeli postawione i przyjęte zostało określenie ruchu
jednostajnie przyspieszonego. Ale czy takie jest przyspieszenie, którym
się natura posługuje przy spadaniu ciężarów, o tym jeszcze wątpię i dlatego sądzę, że tak dla mnie, jak i dla innych, będących podobnego zdania,
potrzeba by przeprowadzić w tym miejscu którekolwiek z doświadczeń, na
których nie zbywa i które by w różnych przypadkach zgadzały się z
wywiedzionemi wnioskami.
SALVIATI: Jak prawdziwy uczony, stawia Waszmość zupełnie uprawnione
żądanie, praktykowane i odpowiednie w naukach, stosujących twierdzenia
matematyczne do wyników naturalnych, jak to widzimy w perspektywie,
astronomii, mechanice, muzyce i innych naukach; wszystkie one
wzmacniają swe zasady przez doświadczenie, stanowiące fundament całej
dalszej budowy: nie sądzę też, aby się wydało zbyteczne, że rozpatrywać
będziemy dłużej tę pierwszą i główną podstawę, na której się opiera
olbrzymi zespół nieskończonej liczby wniosków, których małą część tylko
mamy w tej księdze postawioną przez Autora, a ten dość uczynił, aby
udostępnić dalsze rozważanie tej sprawy. Autor nie pominął
przedstawienia doświadczeń a dla przekonania się o tym, że
przyspieszenie spadających ciał ważkich odbywa się w wyżej
przedstawionym stosunku, wielokrotnie razem z nim w następujący sposób
wykonywałem doświadczenie.
Na liniale, albo raczej na desce drewnianej, 12 łokci długości,
1/2
łokcia szerokości, a 3 cale grubości, na wąskim boku wydrążono rowek,
mający nieco więcej niż 1 cal szerokości. Wyciągnięty był jak
najregularniej prosto, i aby miał gładką powierzchnię, wyklejony
został gładkim i czystym pergaminem; spuszczono biegnącą w tym rowku
okrągłą i gładko obtoczoną kulę z bardzo twardego mosiądzu. Deskę
zawieszano z jednej strony podniesioną, to na jeden, to na dwa łokcie,
po czym puszczano kulę w rowku i w sposób, który zaraz będzie wskazany,
oznaczano czas spadania wzdłuż całego rowka: każde doświadczenie
powtarzano wielokrotnie dla ścisłego wypośrodkowania czasu i nie
znaleziono żadnej różnicy, ani nawet na 1/10
uderzenia pulsu. Następnie puszczano kulę przez ćwierć długości rowka i
znajdowano stale połowę poprzedniego czasu spadania. Brano następnie
inne długości drogi i porównywano mierzony czas spadania z ostatnio
otrzymanym, z jego 2/3, albo 3/4 lub
innymi częściami; przy stokrotnem prawie powtarzaniu otrzymywaliśmy
stale, że drogi są proporcjonalne do kwadratów z czasów: i to dla
każdego nachylenia równi tj. rowka, w którym biegła kula. Znaleźliśmy
przy tym, że przy różnych nachyleniach, czasy obserwowane tak się mają do
siebie, jak to niżej wykazuje i dowodzi nasz Autor. Do mierzenia czasu
używaliśmy kubła pełnego wody, z małym otworem w dnie, przez który
wychodziła cienka żyła wody, łapana w mały kubek, w ciągu każdego
obserwowanego czasu spadania. Zbierana w ten sposób woda była
dokładnie ważona i z różnic ważeń otrzymaliśmy stosunki ciężarów i
stosunki czasów; i to z taką dokładnością, że wielokrotnie powtarzane
obserwacje nie dawały nigdy wydatnej różnicy.
SIMPLICIO: Z wielkiem zadowoleniem byłbym uczestniczył w tych
doświadczeniach, ale przekonany o waszej pilności i wiernym ich
przedstawieniu, jestem spokojny i przyjmuję je jako zupełnie pewne i
prawdziwe.
SALVIATI: Możemy więc wrócić do naszego czytania i iść dalej.
Wniosek II
Wynika po wtóre, że jeżeli od początku ruchu wzięte będą jakiekolwiek
dwie drogi, przebyte w jakichkolwiek czasach, to te czasy mają się do
siebie jak jedna z dróg do średniej proporcjonalnej między dwiema
drogami. Bo przyjmując (rys. 49) początek w S i dwie drogi
ST i SV i oddawszy średnią proporcjonalną SX, będzie się miał czas
spadku po ST do czasu spadku po SV, jak ST do SX; innymi słowy, czas po
SV do czasu po ST jak VS do SX. Bo ponieważ dowiedziono, że drogi mają
się do siebie jak kwadraty z czasów, stosunek zaś dróg VS do ST jest
równy podwójnemu stosunkowi VS do SX, czyli stosunkowi kwadratów z VS i
SX; a więc czasy spadku po SV i ST jak drogi VS do SX.
Scholium
Co dowiedziono dla spadku pionowego, odnosi się także do jakkolwiek
nachylonych równi; na tych równiach stopień przyspieszenia wzrasta w
tym samym stosunku, mianowicie proporcjonalnie do czasu, tj. jak szereg
liczb całkowitych.
SALVIATI: Pragnąłbym tu, Mości Sagredo, abyście mi, choćby to nawet
miało nieco znudzić pana Simplicio, pozwolili przerwać na chwilę
czytanie, abym mógł objaśnić, ile, na zasadzie tego, co dotąd dowiedziono, jak
i opierając się na niektórych wnioskach mechanicznych naszego
Akademika, mogę dodać z pamięci, dla większego wzmocnienia prawdziwości
wniosków, otrzymanych wyżej przez rozumowanie i doświadczenie: ale
przedtem, dla geometrycznego dowodzenia, ważne jest wyprowadzenie
jednego elementarnego twierdzenia pomocniczego, odnoszącego się do
impetów.
SAGREDO: Jeżeli taki ma być nabytek, jak Waszmość obiecuje, to żaden
czas nie będzie dla mnie zbyt długim, aby go z ochotą nie spożytkować,
dla pogłębienia naszej wiedzy o ruchu: i co do mnie, prosić mogę tylko o
zaspokojenie jak najprędzej mej ciekawości; a sądzę że p. Simplicio
jest tego samego zdania.
SIMPLICIO: Nie mogę nic innego powiedzieć.
SALVIATI: Skoro pozwalacie, rozważmy najpierw znane dobrze zjawisko,
że momenty, albo prędkości tegoż samego ciała, przy różnych nachyleniach
równi, są różne i że mają największą wartość przy kierunku prostopadłym
do poziomu, a na równi nachylonej są tym mniejsze, im więcej równia
odchyla się od pionu, toteż impet, zdolność, energia albo, jak
powiemy, moment spadania ciała, zmniejsza się przez równię, na której
ciało się opiera i po której spada.
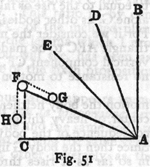 Dla lepszego objaśnienia (rys. 51), niech będzie linia AB,
prostopadła do poziomu AC, stawiana następnie w różnych nachyleniach do
poziomu jak AD, AE, AF itd.; twierdzę, że ciało spadające po
prostopadłej BA będzie miało impet zupełny i największy, mniejszy
spadając po DA, jeszcze mniejszy po EA i wciąż zmniejszający się przy
spadaniu po FA, a w końcu zupełnie wyczerpany na poziomej CA, gdzie ciało
znajduje się w stanie obojętnym tak dla ruchu jak i dla spoczynku i samo
przez się nie ma skłonności do poruszania się w którąkolwiek stronę i
nie stawia żadnego oporu ruchowi; bo ponieważ jest niemożliwe, aby
ciało ważkie lub zespół takich ciał sam przez się podnosił się w górę,
oddalając się od wspólnego środka (commune centro), do którego dążą
wszystkie rzeczy ważkie, to niemożliwe jest także, aby się samo przez
się poruszało, jeżeli by przy takim ruchu jego własny środek ciężkości
nie zbliżał się do wzmiankowanego wspólnego środka: na poziomej więc, która tu oznacza pewną powierzchnię, wszędzie równo
oddaloną od tego środka i dlatego nie mającą żadnego nachylenia, impet
albo moment tego ciała będzie żaden. Odnośnie do tych zmian impetów,
muszę jeszcze zaznaczyć to, co w jednym dawnym traktacie mechaniki,
ułożonym kiedyś w Padwie przez naszego Akademika, wyłącznie dla użytku
jego uczniów, było wyczerpująco i gruntownie dowiedzione, przy okazji
rozważania początku i natury przedziwnego narzędzia, śruby, a
mianowicie badania, w jakim stosunku następuje zmiana impetu przy
różnych nachyleniach równi, jak np. na równi AF, której jeden koniec
jest wzniesiony na wysokość FC nad poziomem i wzdłuż tej wysokości impet
ciała ważkiego i moment spadania jest największy, szuka się tedy, w jakim
stosunku jest ten moment do momentu spadania tegoż ciała po równi FA.
Twierdzę, że ten stosunek jest odwrotnym stosunkiem tych długości i to
właśnie jest twierdzenie pomocnicze, służyć mające przy twierdzeniu,
którego mam nadzieję w następstwie móc dowieść. Jasne jest, że taki jest
impet ciała spadającego, jaki jest opór, albo najmniejsza siła,
wystarczająca do przeszkodzenia spadkowi i zatrzymania: dla zmierzenia
tej siły, czy tego oporu, użyję ciężkości innego ciała. Wyobraźmy sobie
teraz, że na równi FA leży ciało G, zaopatrzone w nitkę, która
przewinięta przez F ma przywiązany
ciężar H i weźmy pod uwagę, że droga spadania albo podnoszenia się
pionowego tego ostatniego, jest wciąż równa całkowitemu podnoszeniu się
lub spadaniu ciała G po równi pochyłej AF, ale nie już jego podnoszeniu
się lub spadaniu pionowemu, w którym to kierunku ciało G (podobnie jak
każde inne) wywiera swój opór, co jest oczywiste; bo biorąc pod uwagę
trójkąt AFC, mamy ruch ciała G np. pod górę, od A do F, złożony z
poprzecznego poziomego AC i prostopadłego CF, a że pierwszy, jak
powiedziano, nie doznaje żadnego oporu (bo przy tym ruchu nie ma żadnego
zmniejszenia lub powiększenia odległości od wspólnego środka wszystkich
ciał, gdyż ta na poziomie pozostaje zawsze ta sama), pozostaje więc
tylko opór przy podnoszeniu się wzdłuż prostopadłej CF. Skoro więc ciało
G, przy ruchu od A do F opiera się tylko podnoszeniu na wysokość CF, a
drugie ciało H w kierunku pionowym przebywa drogę równą spadkowi FA, i
ten stosunek podnoszenia się i opadania pozostaje zawsze ten sam, przy
mniejszym lub większym ruchu tych ciał (gdyż są one ze sobą związane),
możemy więc jak najpewniej twierdzić, że gdy ma nastąpić równowaga tj. stan spoczynku dla ciał, to ich momenty, prędkości, skłonności do
ruchu, tj. drogi, jakieby były przebyte przez te ciała w tym samym
czasie, są do siebie w stosunku odwrotnym do ciężkości tych ciał, co jest
dowiedzione dla wszystkich ruchów mechanicznych, tak że wystarczy do
zatrzymania spadku ciała G, aby ciało H tyle razy mniej ważyło od G, ile
wynosi stosunek FC do FA. Jeżeli więc zrobimy, że tak się ma FA do FC,
jak ciężar G do ciężaru H, to następuje równowaga, bo H i G będą miały
równe momenty i ustanie ich ruch. I skoro tylko umówimy się, że impet,
energia, moment lub skłonność ciała do ruchu tyle wynosi, co siła lub
opór najmniejszy, wystarczający do zatrzymania i gdy dowiedziono, że
ciężar H wystarcza do utrzymywania ruchu ciężaru G, to będzie mniejszy
ciężar H, działający w kierunku pionowym FC całym swym momentem, ścisłą
miarą momentu cząstkowego wywieranego przez ciężar G na równi pochyłej
FA; ale miarą całego momentu tegoż ciężaru G jest sam ten ciężar (gdyż
dla przeszkodzenia spadkowi pionowemu ciężaru użyć trzeba przeciwwagi
tak ciężkiej, jak gdyby ciężar miał swobodę ruchu pionowego); impet
zatem albo moment cząstkowy ciała G wzdłuż równi pochyłej FA, do
całkowitego albo maksymalnego impetu tegoż G na pionowej FC, stać będzie
jak ciężar H do ciężaru G, tj. na rysunku jak prostopadła FC wysokość
równi pochyłej do tejże pochyłej FA i tego mieliśmy dowieść twierdzeniem
pomocniczem, które nasz autor, jak zobaczymy, przyjmuje jako znane w
drugiej części szóstego podania niniejszej rozprawy.
Dla lepszego objaśnienia (rys. 51), niech będzie linia AB,
prostopadła do poziomu AC, stawiana następnie w różnych nachyleniach do
poziomu jak AD, AE, AF itd.; twierdzę, że ciało spadające po
prostopadłej BA będzie miało impet zupełny i największy, mniejszy
spadając po DA, jeszcze mniejszy po EA i wciąż zmniejszający się przy
spadaniu po FA, a w końcu zupełnie wyczerpany na poziomej CA, gdzie ciało
znajduje się w stanie obojętnym tak dla ruchu jak i dla spoczynku i samo
przez się nie ma skłonności do poruszania się w którąkolwiek stronę i
nie stawia żadnego oporu ruchowi; bo ponieważ jest niemożliwe, aby
ciało ważkie lub zespół takich ciał sam przez się podnosił się w górę,
oddalając się od wspólnego środka (commune centro), do którego dążą
wszystkie rzeczy ważkie, to niemożliwe jest także, aby się samo przez
się poruszało, jeżeli by przy takim ruchu jego własny środek ciężkości
nie zbliżał się do wzmiankowanego wspólnego środka: na poziomej więc, która tu oznacza pewną powierzchnię, wszędzie równo
oddaloną od tego środka i dlatego nie mającą żadnego nachylenia, impet
albo moment tego ciała będzie żaden. Odnośnie do tych zmian impetów,
muszę jeszcze zaznaczyć to, co w jednym dawnym traktacie mechaniki,
ułożonym kiedyś w Padwie przez naszego Akademika, wyłącznie dla użytku
jego uczniów, było wyczerpująco i gruntownie dowiedzione, przy okazji
rozważania początku i natury przedziwnego narzędzia, śruby, a
mianowicie badania, w jakim stosunku następuje zmiana impetu przy
różnych nachyleniach równi, jak np. na równi AF, której jeden koniec
jest wzniesiony na wysokość FC nad poziomem i wzdłuż tej wysokości impet
ciała ważkiego i moment spadania jest największy, szuka się tedy, w jakim
stosunku jest ten moment do momentu spadania tegoż ciała po równi FA.
Twierdzę, że ten stosunek jest odwrotnym stosunkiem tych długości i to
właśnie jest twierdzenie pomocnicze, służyć mające przy twierdzeniu,
którego mam nadzieję w następstwie móc dowieść. Jasne jest, że taki jest
impet ciała spadającego, jaki jest opór, albo najmniejsza siła,
wystarczająca do przeszkodzenia spadkowi i zatrzymania: dla zmierzenia
tej siły, czy tego oporu, użyję ciężkości innego ciała. Wyobraźmy sobie
teraz, że na równi FA leży ciało G, zaopatrzone w nitkę, która
przewinięta przez F ma przywiązany
ciężar H i weźmy pod uwagę, że droga spadania albo podnoszenia się
pionowego tego ostatniego, jest wciąż równa całkowitemu podnoszeniu się
lub spadaniu ciała G po równi pochyłej AF, ale nie już jego podnoszeniu
się lub spadaniu pionowemu, w którym to kierunku ciało G (podobnie jak
każde inne) wywiera swój opór, co jest oczywiste; bo biorąc pod uwagę
trójkąt AFC, mamy ruch ciała G np. pod górę, od A do F, złożony z
poprzecznego poziomego AC i prostopadłego CF, a że pierwszy, jak
powiedziano, nie doznaje żadnego oporu (bo przy tym ruchu nie ma żadnego
zmniejszenia lub powiększenia odległości od wspólnego środka wszystkich
ciał, gdyż ta na poziomie pozostaje zawsze ta sama), pozostaje więc
tylko opór przy podnoszeniu się wzdłuż prostopadłej CF. Skoro więc ciało
G, przy ruchu od A do F opiera się tylko podnoszeniu na wysokość CF, a
drugie ciało H w kierunku pionowym przebywa drogę równą spadkowi FA, i
ten stosunek podnoszenia się i opadania pozostaje zawsze ten sam, przy
mniejszym lub większym ruchu tych ciał (gdyż są one ze sobą związane),
możemy więc jak najpewniej twierdzić, że gdy ma nastąpić równowaga tj. stan spoczynku dla ciał, to ich momenty, prędkości, skłonności do
ruchu, tj. drogi, jakieby były przebyte przez te ciała w tym samym
czasie, są do siebie w stosunku odwrotnym do ciężkości tych ciał, co jest
dowiedzione dla wszystkich ruchów mechanicznych, tak że wystarczy do
zatrzymania spadku ciała G, aby ciało H tyle razy mniej ważyło od G, ile
wynosi stosunek FC do FA. Jeżeli więc zrobimy, że tak się ma FA do FC,
jak ciężar G do ciężaru H, to następuje równowaga, bo H i G będą miały
równe momenty i ustanie ich ruch. I skoro tylko umówimy się, że impet,
energia, moment lub skłonność ciała do ruchu tyle wynosi, co siła lub
opór najmniejszy, wystarczający do zatrzymania i gdy dowiedziono, że
ciężar H wystarcza do utrzymywania ruchu ciężaru G, to będzie mniejszy
ciężar H, działający w kierunku pionowym FC całym swym momentem, ścisłą
miarą momentu cząstkowego wywieranego przez ciężar G na równi pochyłej
FA; ale miarą całego momentu tegoż ciężaru G jest sam ten ciężar (gdyż
dla przeszkodzenia spadkowi pionowemu ciężaru użyć trzeba przeciwwagi
tak ciężkiej, jak gdyby ciężar miał swobodę ruchu pionowego); impet
zatem albo moment cząstkowy ciała G wzdłuż równi pochyłej FA, do
całkowitego albo maksymalnego impetu tegoż G na pionowej FC, stać będzie
jak ciężar H do ciężaru G, tj. na rysunku jak prostopadła FC wysokość
równi pochyłej do tejże pochyłej FA i tego mieliśmy dowieść twierdzeniem
pomocniczem, które nasz autor, jak zobaczymy, przyjmuje jako znane w
drugiej części szóstego podania niniejszej rozprawy.
SAGREDO: Z tego, co Waszmość wywiodła, można, jak mi się zdaje łatwo
wywnioskować, gdy się weźmie pod uwagę więcej stosunków odwrotnych, że
momenty jednego i tegoż samego ciała, wzdłuż równi różnego nachylenia,
jak FA, FI, a jednakowej wysokości, są do siebie w stosunku
odwrotnym długości tych równi.
SALVIATI: Wniosek jak najprawdziwszy. Gdy to załatwione, przejdę
teraz do dowiedzenia następującego twierdzenia:
Stopnie prędkości ciała spadającego ruchem naturalnym z tej samej
wysokości, po równiach pochyłych, w jakikolwiek sposób nachylonych, przy
dojściu do poziomu są stale równe, jeżeli usunięto przeszkody.
Ostrzec tu winienem najpierw, że skoro ustalono, iż przy każdYm
nachyleniu, ciało po wyjściu ze spoczynku porusza się z rosnącą
prędkością albo ilością impetu, proporcjonalnie do czasu (zgodnie z
określeniem ruchu naturalnie przyspieszonego, danym przez autora), to,
jak dowiedziono w poprzedniem podaniu, drogi przebyte są do siebie w
podwójnym stosunku czasów, a więc także i stopni prędkości; jakie więc
będą impety pierwszego ruchu, takie proporcjonalnie będą stopnie
prędkości, nabyte w tym samym czasie, bo tak jedne jak i drugie rosną w
tym samym stosunku w ciągu tego czasu.
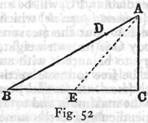 Niech będzie (rys. 52) równia pochyla AB, której
wzniesieniem nad poziom jest prostopadła AC i pozioma BC; a że
dopiero co wywiedziono, że impet ciała spadającego po prostopadłej AC ma
się do impetu tegoż po równi pochyłej AB, jak AB do AC, weźmy na równi
pochyłej AB, do AB i AC trzecią proporcjonalną AD; impet więc po AC ma
się do impetu po AB, czyli po AD, jak AC do AD, a więc ciało, w tym
samym czasie, w jakim by przebiegło drogę prostopadłą AC, przebiegnie
drogę AD po równi pochyłej AB (bo momenty mają się do siebie jak drogi),
a stopień prędkości w C do stopnia prędkości w D będzie się miał jak AC
do AD; ale stopień prędkości w B ma się do tegoż stopnia w D jak czas
spadania po AB do czasu spadania po AD, według określenia ruchu
przyspieszonego, a czas spadania po AB do czasu po AD, jak AC średnia
proporcjonalna między BA i AD do AD, zgodnie z ostatnim wnioskiem
drugiego podania, zatem stopnie prędkości w B i C mają się do stopnia w
D jak AC do AD, a więc są równe, co było twierdzeniem, jakie zamierzono
dowieść.
Niech będzie (rys. 52) równia pochyla AB, której
wzniesieniem nad poziom jest prostopadła AC i pozioma BC; a że
dopiero co wywiedziono, że impet ciała spadającego po prostopadłej AC ma
się do impetu tegoż po równi pochyłej AB, jak AB do AC, weźmy na równi
pochyłej AB, do AB i AC trzecią proporcjonalną AD; impet więc po AC ma
się do impetu po AB, czyli po AD, jak AC do AD, a więc ciało, w tym
samym czasie, w jakim by przebiegło drogę prostopadłą AC, przebiegnie
drogę AD po równi pochyłej AB (bo momenty mają się do siebie jak drogi),
a stopień prędkości w C do stopnia prędkości w D będzie się miał jak AC
do AD; ale stopień prędkości w B ma się do tegoż stopnia w D jak czas
spadania po AB do czasu spadania po AD, według określenia ruchu
przyspieszonego, a czas spadania po AB do czasu po AD, jak AC średnia
proporcjonalna między BA i AD do AD, zgodnie z ostatnim wnioskiem
drugiego podania, zatem stopnie prędkości w B i C mają się do stopnia w
D jak AC do AD, a więc są równe, co było twierdzeniem, jakie zamierzono
dowieść.
Na tej podstawie będziemy teraz mogli łatwiej dowieść następującego
trzeciego podania autora, w którem posługuje się on zasadą, że czas
spadania po równi pochyłej ma się do czasu spadku pionowego jak długość
równi pochyłej do jej wysokości. Bo jeżeli BA jest czas spadania po AB,
to czas spadania po AD będzie średnią między nimi dwiema, a więc równy
AC, według drugiego wniosku drugiego twierdzenia. Ale jeżeli AC jest
czasem spadku po AD, to będzie zarazem czasem spadku po AC, tak że AD i
AC przebywane są w czasach równych i skoro BA jest czasem spadku po
AB, to AC będzie czasem spadku po AC, a więc jak AB do AC, tak się ma
czas po AB do czasu po AC.
Tak samo dowieść można, że czas po AC do czasu po innej równi
pochyłej AE ma się jak AC do AE; skąd ex aequali,
czas po równi pochyłej AB do czasu po równi pochyłej AE ma się również
jak AB do AE itd.
Można by jeszcze, za pomocą takiego samego szeregu twierdzeń, jak to
zaraz zobaczy p. Sagredo, dowieść bezpośrednio szóstego podania autora;
ale dość już tego zbaczania od przedmiotu, które mogło się Waszmościom
wydać zbyt długi, jakkolwiek przyniosło to istotny pożytek w tej kwestii
ruchu.
SAGREDO: Przeciwnie, bardzo mi przypadło do gustu i było
jaknajpotrzebniejsze do dokładnego zrozumienia tej zasady.
SALVIATI: Wracam więc do czytania tekstu.
Twierdzenie III. Podanie III
Jeżeli po równi pochyłej i po prostopadłej, jednakowej wysokości,
wyrusza ze spoczynku to samo ciało, to czasy tych ruchów będą się miały
do siebie jak długości równi i prostopadłej.
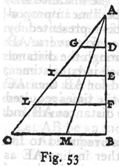 Niech będzie (rys. 53) równia pochyła AC i prostopadła AB,
których wysokość jest jednakowa nad poziomem CB, jest nią mianowicie
sama linia BA: twierdzę, że czas spadku tego ciała po równi AC do czasu
spadku po prostopadłej AB, ma się tak, jak długość równi AC do długości
prostopadłej AB. Poprowadźmy jakiekolwiek linie DG, El, FL, równoległe
do poziomu CB; wiadomo z wyłożonego, że stopnie prędkości ciała,
biegnącego od pierwszego początku ruchu w A, nabyte w punktach G, D, są
równe, bo zbliżenie do poziomu jest jednakowe: podobnie takie będą
stopnie w punktach I, E, jak również w L i F. Jeżeli poprowadzimy
nie tylko te równoległe, lecz inne przechodzące przez wszystkie punkty
linii AB i ciągnące się aż do linii BC, to w punktach końcowych każdej
równoległej momenty czyli stopnie prędkości będą zawsze jednakowe. Drogi
więc AC i AB przebywane będą z tym samym stopniem prędkości. Lecz
dowiedzione było, że jeżeli dwie drogi przebywane są z tymi samymi
stopniami prędkości, to te drogi są proporcjonalne do czasów ruchu;
a więc czas spadania po AC ma się do czasu po AB, jak długość równi AC
do długości prostopadłej AB, c.b.d.d.
Niech będzie (rys. 53) równia pochyła AC i prostopadła AB,
których wysokość jest jednakowa nad poziomem CB, jest nią mianowicie
sama linia BA: twierdzę, że czas spadku tego ciała po równi AC do czasu
spadku po prostopadłej AB, ma się tak, jak długość równi AC do długości
prostopadłej AB. Poprowadźmy jakiekolwiek linie DG, El, FL, równoległe
do poziomu CB; wiadomo z wyłożonego, że stopnie prędkości ciała,
biegnącego od pierwszego początku ruchu w A, nabyte w punktach G, D, są
równe, bo zbliżenie do poziomu jest jednakowe: podobnie takie będą
stopnie w punktach I, E, jak również w L i F. Jeżeli poprowadzimy
nie tylko te równoległe, lecz inne przechodzące przez wszystkie punkty
linii AB i ciągnące się aż do linii BC, to w punktach końcowych każdej
równoległej momenty czyli stopnie prędkości będą zawsze jednakowe. Drogi
więc AC i AB przebywane będą z tym samym stopniem prędkości. Lecz
dowiedzione było, że jeżeli dwie drogi przebywane są z tymi samymi
stopniami prędkości, to te drogi są proporcjonalne do czasów ruchu;
a więc czas spadania po AC ma się do czasu po AB, jak długość równi AC
do długości prostopadłej AB, c.b.d.d.
SAGREDO: Zdaje mi się, że można by to jasno i krótko wywieść z
poprzedniego wniosku, orzekającego, że drogi przebyte ruchem
przyspieszonym, wzdłuż AC i AB, są równe drogom przebytym ruchem
jednostajnym ze stopniem prędkości równym połowie największego stopnia
CB; skoro więc dwie drogi AC i AB przebywane są tym samym ruchem
jednostajnym, to oczywistem jest, na mocy pierwszego podania, że czasy
ruchu są proporcjonalne do dróg.
Wniosek
Wynika stąd, ze czasy spadku, wzdłuż różnie nachylonych równi
jednakowej wysokości są proporcjonalne do długości tych równi. Bo jeżeli
jakakolwiek równia AM schodzi z tegoż samego punktu A i kończy się na
tym samym poziomie CB, to tak samo dowieść można, że czasy spadku po AM
i po AB są proporcjonalne do dróg AM i AB; ale jak czasy wzdłuż AB i AC,
tak samo mają się do siebie linie AB i AC, a więc ex aequali
jak AM do AC, tak się ma czas spadku po AM do czasu spadku po AC.
Twierdzenie IV. Podanie IV
Czasy spadku wzdłuż jednakowo dtugich, a różnie nachylonych równi
pochytych, są do siebie w stosunku odwrotnym pierwiastków kwadratowych z
wysokości tych równi.
(...)
Twierdzenie V. Podanie V
Stosunek czasów spadku po równiach różnego nachylenia, różnej
długości i różnej wysokości, składa się ze stosunku dlugości równi i
odwrotnego stosunku pierwiastków kwadratowych z wysokości.
(...)
Twierdzenie VI. Podanie VI
Jeżeli, czy to z najwyższego punktu, czy też ze spodu koła,
poprowadzimy jakiekolwiek równie pochyłe dochodzące do obwodu, to czasy
spadku po tych równiach będą równe.
(...)
Wniosek I
Wynika stąd, ze czasy spadku po wszystkich przez C i D
przechodzących cięciwach są równe.
Wniosek II
Wynika także, że jeżeli z jednego punktu schodzą prostopadła i równia
pochyla, po których czasy spadku są równe, to mieszczą się one w
półkolu, którego średnicą jest wymieniona prostopadła.
Wniosek III
Wynika jeszcze, że czasy spadku po równiach pochytych są sobie równe
wtedy, gdy wysokości równych części tych równi mają się do siebie, jak
długości tych równi; wiadomo bowiem, że czasy spadku po CA, DA, na
przedostatnim rysunku, są równe, gdy wysokość części AB równej AD,
mianowicie BE, tak się ma do wysokości D F, jak CA do DA.
SAGREDO: Zechce Waszmość
przerwać na chwilę czytanie, póki nie wyjaśnię sobie jednej myśli, którą
właśnie powziąłem, a która, o ile nie jest mrzonką, zbliża się do
wdzięcznej igraszki, jak te wszystkie zdarzające się w naturze lub z
konieczności.
Widać, że, jeżeli z jednego punktu płaszczyzny poziomej
poprowadzimy na tej płaszczyźnie linie proste we wszystkich kierunkach i
przypuścimy, że po każdej z tych linii porusza się jeden punkt ruchem
jednostajnym, a przy tym wszystkie te punkty wychodzą w tym samym czasie
z punktu oznaczonego i prędkość ich jest jednakowa, to będą one
wszystkie stale i zawsze znajdować się na wciąż rosnącym okręgu koła i
wszystkie te koła mieć będą wspólny środek w punkcie oznaczonym,
zupełnie w ten sam sposób, jak na powierzchni wody stojącej kamyk, który
spada z wysokości wytwarza swym uderzeniem małe pole rozchodzące się we
wszystkich kierunkach, wciąż rosnącymi kręgami. Lecz jeżeli ustawimy
płaszczyznę prostopadle do poziomu i u jej szczytu oznaczymy jeden
punkt, z którego rozchodzić się będą na tej płaszczyźnie, w różnych
kierunkach możliwych, linie nachylone, a po tych liniach spadać będą
ciężary ruchem naturalnie przyspieszonym, to jak się ułożą te ciężary,
przyjmując, że pozostają wciąż widoczne? Budzi to mój podziw, że
zgodnie z poprzedniemi podaniami, widzieć będziemy zawsze, że wszystkie
znajdują się na wciąż rosnącym okręgu koła, w miarę jak spadając
oddalają się od punktu wyjścia: i dla lepszego objaśnienia (rys. 58) naznaczmy punkt najwyższy A, z którego rozchodzą się linie
jakkolwiek nachylone AF, AM, a także pionowa AB, na której leżą C, D,
środki obu kół przechodzących przez A, a przecinających obie linie
nachylone w punktach F, H, B, E, G, I. Widać z poprzednich
dowodzeń, że jeżeli ciała wyruszają równocześnie z A w różnych
kierunkach, to znajdować się one będą równocześnie jedno w E, drugie w
G, trzecie w I i dalej spadając dojdą równocześnie do F, H, B i tak
dalej, nieskończenie wiele ciał dochodzić będzie równocześnie do coraz
większych okręgów kół aż do nieskończoności. Z dwóch więc rodzajów
ruchu, którymi posługuje się natura, powstaje cudownie odpowiadająca
różność nieskończonej liczby kół. Tam widzimy siedlisko i początek w
środku nieskończenie wielu kół współśrodkowych, a tu w najwyższym punkcie
styczność nieskończenie wielu kół różnośrodkowych. Jedne powstają z
ruchu równego i jednostajnego, a drugie z ruchów samych w sobie
nierównych, różnych jeden od drugiego i odbywających się po
nieskończonej liczbie różnych nachyleń. Ale dodamy nadto, ze jeżeli z
obu wymienionych punktów poprowadzimy linie, nie tylko na płaszczyźnie
pionowej i poziomej, ale we wszystkich kierunkach przestrzeni, to
ujrzymy, zamiast kół wychodzących jak poprzednio z obu punktów,
powstającą nieskończoność kul, albo lepiej kulę rosnącą do
nieskończoności. I to w dwojaki sposób, raz z początkiem w środku, a
drugi raz na obwodzie takich kul.
SALVIATI: Jest to zaiste bardzo piękna myśl, odpowiadająca bystrości
pana Sagredo.
SIMPLICIO: Zrozumiałem tę myśl odnośnie do obu sposobów, w jaki się
tworzą koła lub kule, odpowiednio do dwóch rodzajów ruchu naturalnego,
jakkolwiek powstawanie kół przy ruchu przyspieszonym nie jest dla mnie
jasne w swej całości; w każdym razie
możność oznaczania początku ruchu, już to w środku już też na szczycie
powierzchni kulistej, każe mi myśleć, że zachodzi tu może jakaś wielka
tajemnica, w tych prawdziwych a cudownych wnioskach; mam tu na myśli
tajemnicę dotyczącą stworzenia świata, uważanego za mający kształt
kulisty i siedlisko pierwszej przyczyny.
SALVIATI: Nie wzbraniałbym się i w to uwierzyć, ale sądzę, że
podobnie głębokie rozważania związane są z naukami wyższymi od tych,
jakie nas zajmują. Nam powinno wystarczać, gdy będziemy tymi
podrzędniejszymi pracownikami, którzy odnajdują i wydobywają marmur w
kopalni, z którego później pomysłowi rzeźbiarze tworzą cudowne postaci,
znajdujące się w ukryciu pod grubą i bezkształtną powłoką. Jeżeli więc
pozwolicie pójdziemy dalej.
Twierdzenie VII. Podanie VII
Jeżeli wysokości dwóch równi mają się do siebie jak kwadraty z ich
długości, to czasy spadku po tych równiach od wyjścia ze spoczynku
będą sobie równe.
(...)
Twierdzenie VIII. Podanie VIII
Na równiach, wychodzących z punktów postawionego na poziomie
okręgu koła, a dochodzących do dolnego lub górnego końca średnicy
pionowej, czasy spadku są równe czasowi spadku po średnicy: na równiach
nie dochodzących do średnicy są krótsze, a na przecinających średnicę
dłuższe.
(...)
Twierdzenie IX. Podanie IX
Jeżeli z punktu, wziętego na linii poziomej, schodzą dwie
jakkolwiek nachylone równie i zostaną przecięte linią tworzącą z nimi
kąty, równe na przemian nachyleniom równi, to czasy spadku po równiach,
od punktu początkowego do przecięć z linią sieczną, będą sobie równe.
(...)
Twierdzenie X. Podanie X
Czasy spadku po równiach różnego nachylenia a równej wysokości, mają
się do siebie jak długości tych równi, bez względu na to, czy ruch się
zaczyna od punktu wyjścia ze spoczynku czy też od punktów jednakowej
wysokości.
(...)
Twierdzenie XI. Podanie XI
Jeżeli równia, po której odbywa się ruch, zaczynając od spoczynku, w
jakikolwiek sposób zostanie podzielona, to czasy spadku po dwóch jej
częściach mają do siebie jak długość pierwszej części do przewyżki ponad
tę część średniej geometrycznej, między długością całej równi a tąż
pierwszą częścią.
(...)
Twierdzenie XII. Podanie XII
Jeżeli prostopadła i równia jakkolwiek nachylona przecinają się
miedzy dwiema liniami poziomymi i jeżeli weźmiemy średnie
proporcjonalne między ich długościami a długościami ich części
zawartych między wzajemnym ich przecięciem a górną linią poziomą, to
czas spadku po prostopadtej ma się do czasu spadku po linii złożonej z
górnej części prostopadłej i dolnej nachylonej jak cała długość
prostopadłej do sumy dwóch dróg, z których jedna jest średnią
proporcjonalną między prostopadłymi, a druga przewyżką całej równi
pochyłej nad średnią proporcjonalną między długościami całej równi i
jej części dolnej.
(...)
Zadanie I. Podanie XIII
Mając daną prostopadłą, dostawić do jej spodu równię pochylą, tej
samej wysokości, ale taką aby spadek po niej, następujący w dalszym
ciągu spadku po prostopadłej, odbywał się w tym samym czasie, jak po
prostopadłej od wyjścia ze spoczynku.
(...)
Zadanie II. Podanie XIV
Dane są: prostopadła i równia do niej nachylona; odciąć długość na
górnej części prostopadłej taką, aby od wyjścia ze spoczynku w tym samym
czasie została przebyta co i równia pochyła w dalszym ciągu spadku po
przebyciu szukanego odcinka.
(...)
Zadanie III. Podanie XV
Dane są: prostopadła i równia do niej nachylona; na dolnem
przedłużeniu prostopadlej wyznaczyć odcinek, który by w dalszym ciągu
spadku wzdłuż danej prostopadlej, przebyty był w tym samym czasie co i
równia pochyła w dalszym ciągu tego spadku.
(...)
Twierdzenie XIII. Podanie XVI
Jeżeli części równi pochyłej i prostopadłej, czasy spadku po których
od wyjścia ze spoczynku są równe, zaczynają się w jednym i tym samym
punkcie, to ciało spadające z jakiejkolwiek wysokości przebywać będzie
drogę po równi pochytej prędzej niż po prostopadłej.
(...)
Wniosek
 Z tego i z poprzedniego wynika, że droga, która po spadku z wyższego
punktu przebywana jest w tym samym czasie po prostopadłej i po równi
pochyłej, jest mniejszą od drogi, przebytej w tym samym czasie po równi
pochyłej, ale niepoprzedzonej spadkiem z wyższego punktu, a znów
większą od samej równi pochyłej, gdyż dowiedziono poprzednio, że w
dalszym ciągu (rys. 71) spadku z wyższego punktu A czas spadku
wzdłuż EC jest krótszy niż poprzedzający po EB, a więc droga przebywana
w czasie spadku po EB równym czasowi spadku po EC jest mniejsza od
całej drogi EB. Że zaś ta droga prostopadła jest większa od EC, to okaże
się jasne po rozpatrzeniu rysunku poprzedniego podania, gdzie
dowiedziono, że droga prostopadła BG przebyta zostaje w tym samym czasie
co i droga BC w dalszym ciągu spadku po AB: że zaś BG jest większe od
BC, tak się dowodzi. Ponieważ BE i FB są sobie równe, a BA mniejsze od
BD, przeto większy jest stosunek FB do BA aniżeli EB do BD, a stąd FA do
AB większy aniżeli ED do DB; tak się ma zatem FA do AB. jak GF do FB
(jest bowiem AF średnią proporcjonalną między BA i AG), i podobnie jak
ED do BD, tak się ma CE do EB; więc stosunek GB do BF jest większy
aniżeli CB do BE, a więc GB większe od BC.
Z tego i z poprzedniego wynika, że droga, która po spadku z wyższego
punktu przebywana jest w tym samym czasie po prostopadłej i po równi
pochyłej, jest mniejszą od drogi, przebytej w tym samym czasie po równi
pochyłej, ale niepoprzedzonej spadkiem z wyższego punktu, a znów
większą od samej równi pochyłej, gdyż dowiedziono poprzednio, że w
dalszym ciągu (rys. 71) spadku z wyższego punktu A czas spadku
wzdłuż EC jest krótszy niż poprzedzający po EB, a więc droga przebywana
w czasie spadku po EB równym czasowi spadku po EC jest mniejsza od
całej drogi EB. Że zaś ta droga prostopadła jest większa od EC, to okaże
się jasne po rozpatrzeniu rysunku poprzedniego podania, gdzie
dowiedziono, że droga prostopadła BG przebyta zostaje w tym samym czasie
co i droga BC w dalszym ciągu spadku po AB: że zaś BG jest większe od
BC, tak się dowodzi. Ponieważ BE i FB są sobie równe, a BA mniejsze od
BD, przeto większy jest stosunek FB do BA aniżeli EB do BD, a stąd FA do
AB większy aniżeli ED do DB; tak się ma zatem FA do AB. jak GF do FB
(jest bowiem AF średnią proporcjonalną między BA i AG), i podobnie jak
ED do BD, tak się ma CE do EB; więc stosunek GB do BF jest większy
aniżeli CB do BE, a więc GB większe od BC.
Zadanie IV. Podanie XVII
Dane są: prostopadła i dochodząca do niej równia pochyła. Oznaczyć
na tej ostatniej drogę, która by w dalszym ciągu spadku po prostopadłej była
przebyta w tym samym czasie, co droga po prostopadłej od wyjścia ze
spoczynku.
(...)
Zadanie V. Podanie XVIII
Na prostopadłej, od początku ruchu, odcięta jest droga przebywana
w danym czasie, i dany jest inny czas krótszy; oznaczyć na tej
prostopadlej inną drogę, która była by przebyta w tym danym krótszym
czasie.
(...)
Zadanie VI. Podanie XIX
Dana jest jakakolwiek droga na prostopadłej, od punktu wyjścia ze
spoczynku i dany czas spadku: oznaczyć czas, w ciągu którego przebyta
zostanie przez to samo ciało droga tej samej długości, wzięta w innym
miejscu prostopadłej.
(...)
Wniosek
Wynika stąd, że jeżeli czas spadku po jakiej drodze, od punktu
wyjścia ze spoczynku, jest równy tej drodze, to czas spadku po tej
drodze, w dalszym ciągu spadku po części dodanej, będzie równy
przewyżce średniej proporcjonalnej między sumą obu dróg i daną drogą,
ponad średnią proporcjonalną między daną drogą i częścią dodaną. Bo
jeżeli (rys. 75) czas spadku po AB, od punktu wyjścia ze
spoczynku w A jest AB, to po dodaniu części AS mieć będziemy czas spadku
po AB w dalszym ciągu spadku po SA równy przewyżce średniej
proporcjonalnej między SB i BA ponad średnią proporcjonalną między BA i
AS.
Zadanie VII. Podanie XX
Dana jest jakakolwiek droga i na niej część przy początku;
oznaczyć inną część na drugim końcu, która by była przebyta w tym
samym czasie co i pierwsza cześć dana.
(...)
Twierdzenie XIV. Podanie XXI
Jeżeli spadek odbywa się po prostopadłej od wyjścia ze spoczynku
i od początku ruchu przebyta zostanie pewna część drogi w ciągu
pewnego czasu, a następnie ciało spada po jakiejkolwiek równi pochyłej,
to droga, w tym samym czasie po tej równi przebyta, będzie od drogi
przebytej po prostopadłej więcej niż dwa razy, a mniej niż trzy razy
większą.
(...)
Zadanie VIII. Podanie XXII
Dane są dwa nierówne odstępy czasu, oraz droga wzdłuż
prostopadłej przebywana po wyjściu ze spoczynku w ciągu krótszego odstępu;
poprowadzić z wierzchołka prostopadłej równię pochyłą taką, aby
dochodziła do poziomu i była przebyta w ciągu dłuższego z dwóch danych
odstępów czasu.
(...)
Zadanie IX. Podanie XXIII
Dana jest droga po prostopadłej, przebyta od początku wyjścia
ze spoczynku; przeprowadzić przez jej koniec równię pochyłą taką, aby w
dalszym ciągu spadku po prostopadłej, część jej danej długości w tym
samym czasie była przebyta i aby ta część była większa niż dwa razy, a
mniejsza niż trzy razy, dana droga po prostopadłej.
(...)
Scholium
 Rozpatrując uważnie widzimy, że im mniejsza jest różnica
(rys. 81) pomiędzy linią IR a potrojonym AC, tym bardziej zbliża się równia
pochyła drugiego ruchu, to jest CO, do prostopadłej, po której w końcu
przebyta zostaje w czasie równym AC droga równa potrojonemu AC. Bo
im więcej IR zbliża się do potrojonego AC, tym bliższe będzie IM
zrównania się z MN. A ponieważ jak IM do MN na rysunku, tak będzie AC do
CE, to CE będzie mało co większym od AC i co zatem będzie punkt E bardzo
bliski punktu A, a CO i CS przecinać się będą pod bardzo ostrym kątem,
zlewając się ze sobą. Ale znów jeżeli IR będzie bardzo mało większa od
podwojonego tegoż AC, to IM będzie króciutką linią, wskutek czego AC
będzie bardzo małe w porównaniu z CE, które stanie się bardzo długie
i zbliżać się będzie do równoległej do poziomu, poprowadzonej przez C.
Wnosić stąd można, że jeżeli, jak na rysunku, w dalszym ciągu spadku po
równi pochyłej AC następuje odbicie, kierujące ciało wzdłuż linii
poziomej, jaką jest CT, to w ciągu czasu równego AC ciało przebiegnie
drogę równą zdwojonemu AC. I tu więc, jak widzimy, stosuje się podobne
rozumowanie. Wynika zaś stąd, że ponieważ tak się ma OE do OF, jak FE do
EC, to FC jest miarą czasu spadku po CO. Ale jeżeli część pozioma TC
jest równa zdwojonemu AC, to przepołówmy ją w V, a jej przedłużenie ku X
będzie nieskończenie wielkie, gdyż jej przecięcie z AE wymaga, aby
stosunek nieskończonego TX do nieskończonego VX nie był inny jak
stosunek nieskończonego VX do nieskończonego XC.
Rozpatrując uważnie widzimy, że im mniejsza jest różnica
(rys. 81) pomiędzy linią IR a potrojonym AC, tym bardziej zbliża się równia
pochyła drugiego ruchu, to jest CO, do prostopadłej, po której w końcu
przebyta zostaje w czasie równym AC droga równa potrojonemu AC. Bo
im więcej IR zbliża się do potrojonego AC, tym bliższe będzie IM
zrównania się z MN. A ponieważ jak IM do MN na rysunku, tak będzie AC do
CE, to CE będzie mało co większym od AC i co zatem będzie punkt E bardzo
bliski punktu A, a CO i CS przecinać się będą pod bardzo ostrym kątem,
zlewając się ze sobą. Ale znów jeżeli IR będzie bardzo mało większa od
podwojonego tegoż AC, to IM będzie króciutką linią, wskutek czego AC
będzie bardzo małe w porównaniu z CE, które stanie się bardzo długie
i zbliżać się będzie do równoległej do poziomu, poprowadzonej przez C.
Wnosić stąd można, że jeżeli, jak na rysunku, w dalszym ciągu spadku po
równi pochyłej AC następuje odbicie, kierujące ciało wzdłuż linii
poziomej, jaką jest CT, to w ciągu czasu równego AC ciało przebiegnie
drogę równą zdwojonemu AC. I tu więc, jak widzimy, stosuje się podobne
rozumowanie. Wynika zaś stąd, że ponieważ tak się ma OE do OF, jak FE do
EC, to FC jest miarą czasu spadku po CO. Ale jeżeli część pozioma TC
jest równa zdwojonemu AC, to przepołówmy ją w V, a jej przedłużenie ku X
będzie nieskończenie wielkie, gdyż jej przecięcie z AE wymaga, aby
stosunek nieskończonego TX do nieskończonego VX nie był inny jak
stosunek nieskończonego VX do nieskończonego XC.
Do tego samego wyniku dojść by można inną drogą, powtarzając
rozumowanie użyte przy dowodzeniu pierwszego podania. Bo weźmy pod
uwagę (rys. 81) trójkąt ABC, w którym linie równoległe do
podstawy BC przedstawiają stopnie prędkości odpowiadające rosnącym
czasom spadku; liniami tymi, ponieważ jest ich nieskończenie wiele, jak
i punktów na linii AC i chwil w każdym czasie, wypełniona jest cała
powierzchnia trójkąta. Jeżeli przyjmiemy, że ruch odbywać się będzie w
ciągu tego samego czasu, co ruch poprzedni, ale już nie jako
przyspieszony, tylko jako jednostajny, z największym stopniem prędkości
nabytej, której to stopień przedstawia linia BC, to z tych stopni
prędkości złoży się prostokąt ADBC, będący zdwojeniem trójkąta ABC.
Droga przebyta tym ruchem jednostajnym będzie równa podwójnej drodze
przebytej ze stopniami prędkości, jakie przedstawia trójkąt ABC. Ale na
płaszczyźnie poziomej ruch jest jednostajny, bo nie ma tam żadnej
przyczyny przyspieszenia lub opóźnienia; wynika stąd, że droga CD
przebyta w czasie AC będzie dwa razy większa od drogi AC, bo ruch
przyspieszony odbywa się, od wyjścia ze spoczynku, według równoległych
trójkąta, a ruch jednostajny według równoległych prostokąta, które, w
swej liczbie nieskończone, wynoszą dwa razy tyle, co nieskończone
również równoległe trójkąta.
Zauważyć wypada nadto, że stopień prędkości, jakkolwiek się w ciele
objawia, jest w nim niezniszczalnie zawarty, podczas gdy przyczyny
zewnętrzne wytwarzają przyspieszenie lub opóźnienie, co tylko spostrzec
można na płaszczyźnie poziomej: bo przy spadku po pochyłości dołącza
się przyczyna przyspieszenia, a przy podnoszeniu się - opóźnienia.
Wynika stąd również, że ruch po poziomie jest także wieczny, bo gdy
pozostaje zawsze jednaki, nie osłabia się ani wzmacnia, nie zmniejsza
się i nie powiększa. I dalej, ponieważ osiągany przy swobodnym spadku
stopień prędkości, jest niezniszczalną i wieczną ciała spadającego
własnością, to jasne jest, że gdy po spadku wzdłuż równi pochyłej
następuje odbicie na inną równię podnoszącą się, to tam zjawia się
przyczyna opóźnienia; gdyż na takiej równi to samo ciało swobodnie
spada, bo następuje tam zmieszanie przeciwnych sobie skłonności, to jest
stopnia prędkości osiągniętego przy poprzedniem spadaniu, który by sam
przez się ciało do nieskończoności jednostajnie posuwał i naturalnej
skłonności do ruchu z góry na dół, z tym samym stosunkiem
przyspieszenia, według którego ciało zawsze się porusza. Wydaje się
przeto zrozumiałe, jeżeli badamy zaznaczone przyczyny, że ciało, które
spadało wzdłuż równi pochyłej i zostało odbite na równię podnoszącą się,
zatrzymuje w sobie osiągnięty przy spadku stopień prędkości,
jednocześnie wszakże poddaje się naturalnej skłonności do spadania, to
jest ruchowi od wyjścia ze spoczynku przyspieszonemu, w stosunku zawsze
przyjmowanym. Co, gdyby dla dobrego zrozumienia było nieco ciemne,
jaśniej wyłożone zostanie na rysunku.
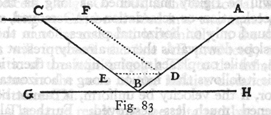 Przypuśćmy, że spadek się odbywa (rys. 83) po równi pochyłej
AB, po czym, wzdłuż innej równi podnoszącej się BC, następuje ruch
odbity, oraz że te równie są jednakowej długości i pod jednaowymi kątami
nachylone do poziomu GH. Wiadomo, że ciało, wychodzące ze spoczynku w A
i spadające po AB osiąga stopnie prędkości w miarę wzrostu czasu;
stopień w B, największy z osiągniętych, będzie z natury niezmiennie
pozostawał w ciele, jeżeli się nie zjawią nowe przyczyny przyspieszenia
lub opóźnienia; przyspieszenia, jeżeli ciało dalej spada, opóźnienia -
jeżeli po odbiciu podnosi się wzdłuż BC; na poziomej zaś GH ruch
ciągnąłby się do nieskończoności ze stopniem prędkości osiągniętym przez
spadek od A do B. A prędkość ta jest taka, że w ciągu czasu równego
czesowi spadku wzdłuż AB, przebyta by została wzdłuż poziomej droga
równa 2AB. Przypuśćmy teraz, że ciało porusza się z tym samym stopniem
prędkości jednostajnie wzdłuż BC, w ten sposób, że w tym samym, co
dopiero wymienionym czasie przebyta byłaby wzdłuż BC droga równa 2AB. W
rzeczywistości jednak widzimy, że ciało, zaraz gdy się zacznie podnosić,
poddane będzie tym samym wpływom, jak przy spadku wzdłuż AB, bo spadając
po BC osiągnęłoby tę samą prędkość i przebyło tę samą drogę w tym samym
czasie jak wzdłuż AB; oczywiście to zmieszanie (mixtio) ruchów,
jednostajnego pod górę, a przyspieszonego na dół, doprowadzi ciało po
równi BC do końca C, w którym osiągnięte zostaną równe stopnie
prędkości. Jeżeli weźmiemy po obu stronach punkty D, E, równo oddalone
od B, to czas spadku po DB jest równy czasowi odbicia wzdłuż BE, co tak
możemy dowieść. Poprowadzimy DF, równoległą do BC; wiadomo, że po spadku
wzdłuż AD następuje odbicie wzdłuż DF. Lecz jeżeli z D ciało biegłoby
dalej poziomo wzdłuż DE, to prędkość w E byłaby taka sama jak w D i
ciało podniosłoby się od E do C. Słusznie więc możemy twierdzić, że
jeżeli w dalszym ciągu spadku po jakiejkolwiek równi pochyłej,
następuje odbicie wzdłuż równi podnoszącej się, to ciało, wskutek
nabytego impetu wzniesie się do tej samej wysokości, czyli wzniesienia
nad poziomem. Gdy spada wzdłuż (rys. 82) AB, ciało podnosi się
wzdłuż płaszczyzny odbicia BC aż do poziomej AC; nie tylko wtedy, gdy
nachylenia równi są jednakowe, ale także gdy są nierówne, jak równia BD.
Bo na równiach o różnym nachyleniu, lecz jednakowej wysokości nabywane są
jednakowe stopnie prędkości. Jeżeli EB, BD są jednakowo nachylone, to
spadek wzdłuż ED podnosi ciało wzdłuż BD aż do D, bo taki impuls nadaje
mu impet prędkości w punkcie B; impet zaś w B jest jednakowy, czy ciało
spada wzdłuż AB, czy wzdłuż EB; wiadomo, że ciało, po swym spadku po AB
jednakowo popychane jest po BD, jak i po EB. Prawda, że czas podniesienia
po BD jest dłuższy niż po BC, jak i czas spadku po EB dłuższy niż po AB:
stosunek zaś tych czasów jest równy stosunkowi długości samych równi.
Wypada nam jeszcze znaleźć stosunek dróg przebytych wzdłuż równi różnego
nachylenia i różnej wysokości, a w równych czasach: a więc zbadać spadek
między dwiema równoległymi poziomymi. Ten zaś odbywa się według
następującego stosunku.
Przypuśćmy, że spadek się odbywa (rys. 83) po równi pochyłej
AB, po czym, wzdłuż innej równi podnoszącej się BC, następuje ruch
odbity, oraz że te równie są jednakowej długości i pod jednaowymi kątami
nachylone do poziomu GH. Wiadomo, że ciało, wychodzące ze spoczynku w A
i spadające po AB osiąga stopnie prędkości w miarę wzrostu czasu;
stopień w B, największy z osiągniętych, będzie z natury niezmiennie
pozostawał w ciele, jeżeli się nie zjawią nowe przyczyny przyspieszenia
lub opóźnienia; przyspieszenia, jeżeli ciało dalej spada, opóźnienia -
jeżeli po odbiciu podnosi się wzdłuż BC; na poziomej zaś GH ruch
ciągnąłby się do nieskończoności ze stopniem prędkości osiągniętym przez
spadek od A do B. A prędkość ta jest taka, że w ciągu czasu równego
czesowi spadku wzdłuż AB, przebyta by została wzdłuż poziomej droga
równa 2AB. Przypuśćmy teraz, że ciało porusza się z tym samym stopniem
prędkości jednostajnie wzdłuż BC, w ten sposób, że w tym samym, co
dopiero wymienionym czasie przebyta byłaby wzdłuż BC droga równa 2AB. W
rzeczywistości jednak widzimy, że ciało, zaraz gdy się zacznie podnosić,
poddane będzie tym samym wpływom, jak przy spadku wzdłuż AB, bo spadając
po BC osiągnęłoby tę samą prędkość i przebyło tę samą drogę w tym samym
czasie jak wzdłuż AB; oczywiście to zmieszanie (mixtio) ruchów,
jednostajnego pod górę, a przyspieszonego na dół, doprowadzi ciało po
równi BC do końca C, w którym osiągnięte zostaną równe stopnie
prędkości. Jeżeli weźmiemy po obu stronach punkty D, E, równo oddalone
od B, to czas spadku po DB jest równy czasowi odbicia wzdłuż BE, co tak
możemy dowieść. Poprowadzimy DF, równoległą do BC; wiadomo, że po spadku
wzdłuż AD następuje odbicie wzdłuż DF. Lecz jeżeli z D ciało biegłoby
dalej poziomo wzdłuż DE, to prędkość w E byłaby taka sama jak w D i
ciało podniosłoby się od E do C. Słusznie więc możemy twierdzić, że
jeżeli w dalszym ciągu spadku po jakiejkolwiek równi pochyłej,
następuje odbicie wzdłuż równi podnoszącej się, to ciało, wskutek
nabytego impetu wzniesie się do tej samej wysokości, czyli wzniesienia
nad poziomem. Gdy spada wzdłuż (rys. 82) AB, ciało podnosi się
wzdłuż płaszczyzny odbicia BC aż do poziomej AC; nie tylko wtedy, gdy
nachylenia równi są jednakowe, ale także gdy są nierówne, jak równia BD.
Bo na równiach o różnym nachyleniu, lecz jednakowej wysokości nabywane są
jednakowe stopnie prędkości. Jeżeli EB, BD są jednakowo nachylone, to
spadek wzdłuż ED podnosi ciało wzdłuż BD aż do D, bo taki impuls nadaje
mu impet prędkości w punkcie B; impet zaś w B jest jednakowy, czy ciało
spada wzdłuż AB, czy wzdłuż EB; wiadomo, że ciało, po swym spadku po AB
jednakowo popychane jest po BD, jak i po EB. Prawda, że czas podniesienia
po BD jest dłuższy niż po BC, jak i czas spadku po EB dłuższy niż po AB:
stosunek zaś tych czasów jest równy stosunkowi długości samych równi.
Wypada nam jeszcze znaleźć stosunek dróg przebytych wzdłuż równi różnego
nachylenia i różnej wysokości, a w równych czasach: a więc zbadać spadek
między dwiema równoległymi poziomymi. Ten zaś odbywa się według
następującego stosunku.
Twierdzenie XV. Podanie XXIV
Między dwiema poziomymi równoległymi dana jest prostopadła, przez
której spód przechodzi równia pochyla. Po spadku wzdłuż prostopadłej,
droga przebyta przy podnoszeniu się ciała po równi, w ciągu czasu równego
czasowi spadku, jest większa od długości prostopadłej, a mniejsza od
podwojonej tejże długości.
(...)
Twierdzenie XVI. Podanie XXV
Jeżeli w dalszym ciągu spadku po jakiejkolwiek równi pochyłej,
następuje ruch po płaszczyźnie poziomej, to czas spadku po równi ma się
do do czasu ruchu wzdłuż jakiejkolwiek linii poziomej, jak podwójna
długość równi do przyjętej linii poziomej.
(...)
Zadanie X. Podanie XXVI
Dana jest prostopadła między dwiema poziomymi, a także długość
większa od długości prostopadłej, a mniejsza od tejże podwojonej; przez spód prostopadłej przeprowadzić równię pochyłą taką, aby przy
podnoszeniu się po niej w dalszym ciągu spadku po prostopadłej, ciało
przebyto długość równą danej, w czasie równym czasowi spadku po
prostopadłej.
(...)
Twierdzenie XVII. Podanie XXVII
Jeżeli ciało spada wzdłuż dwóch równi różnego nachylenia, a tej
samej wysokości, to droga przebyta w dolnej części równi dłuższej, w tym
samym czasie co cała równia krótsza, jest równa sumie dwóch dróg, z
których jedna jest tej długości co równia krótsza, a druga tak się ma do
krótszej, jak dłuższa do przewyżki dłuższej nad krótszą.
(...)
Twierdzenie XVIII. Podanie XXVIII
Pozioma AG (rys. 87) jest
styczną do kąta. Z punktu styczności prowadzimy średnice AB i dwie
cięciwy AE, EB. Oznaczyć stosunek czasu spadku po AB do czasu spadku
wzdłuż AE i EB.
(...)
Zadanie XI. Podanie XXIX
Dana jest długość pozioma, na której końcu wystawiona została
prostopadła, a na tej prostopadłej odcięta połowa danej długości
poziomej; ciało, spadające z tej wysokości, a następnie zwrócone na
poziomą, przebiegnie obie te drogi w krótszym czasie niż jakąkolwiek
inną długość prostopadłej razem z daną długością poziomą.
(...)
Twierdzenie XIX. Podanie XXX
Jeżeli z pewnego punktu linii poziomej schodzi prostopadła do
niej, a z innego punktu tejże poziomej
poprowadzona zostanie do tej prostopadlej równia pochyła taka, że ciało w
najkrótszym czasie z poziomej spada po tej równi na prostopadłą, to ta
równia będzie odcinać na prostopadłej długość równą odległości między
dwoma punktami wziętymi na poziomej.
(...)
Twierdzenie XX. Podanie XXXI
Jeżeli linia prosta leżąca nad poziomą jest jakkolwiek do niej
nachylona, to równia pochyla przechodząca przez jakikolwiek punkt
poziomej i ciągnąca się do linii nachylonej, po której spadek trwa
najkrócej, dzielić będzie na dwie połowy kąt między prostopadłymi z
danego punktu wyprowadzonymi, jedna do poziomej, a druga do równi
pochyłej.
(...)
Lemat
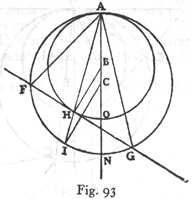
Jeżeli dwa koła są styczne wewnętrznie, a koło wewnętrzne jest
styczne do jakiejkolwiek linii prostej, przecinającej koło zewnętrzne,
to trzy proste przeprowadzone od punktu styczności kół do trzech punktów
linii stycznej, mianowicie do punktu jej styczności z kołem wewnętrznym
i do punktów jej przecinania się z kołem zewnętrznym, tworzą między
sobą kąty równe.
W punkcie A (rys. 93) stykają się dwa koła, których środki
są B mniejszego, C większego: styczną do koła mniejszego jest
jakakolwiek prosta FG w punkcie H, przecinająca koło większe w punktach
F i G, a dochodzą do niej trzy linie AF, AH, AG, między którymi zawarte
kąty FAH, GAH są równe. Przedłużmy AH do spotkania okręgu w I,
poprowadźmy ze środków BH, CI, a przez te środki przeprowadźmy BC i
przedłużmy do A i do O i N. A ponieważ kąty ICN, HBO są równe, bo każdy
z nich jest dwa razy większy od IAN, to linie BH i Cl będą równoległe.
Ze zaś BH idąca od środka do punktu styczności jest prostopadła do FG i
do tejże jesi prostopadła CI i łuk FI równy łukowi IG, więc kąt FAI jest
równy kątowi IAG, c.b.d.d.
Twierdzenie XXI. Podanie XXXII
Jeżeli na poziomie weźmiemy dwa punkty i przez jeden z nich
poprowadzimy prostą jakkolwiek nachyloną w stronę drugiego, to
połączywszy drugi punkt z punktem linii nachylonej, tak oddalonym od
jej początku, jak oddalone są od siebie oba punkty na poziomie, mieć
będziemy spadek wzdłuż tej linii łączącej trwający krócej aniżeli wzdłuż
jakiejkolwiek innej linii, poprowadzonej z tego samego punktu do linii
nachylonej. Wzdłuż innych linii o równe kąty od pierwszej odchylonych,
czasy spadku będą sobie równe.
(...)
Zadanie XII. Podanie XXXIII
Dana jest prostopadła i równia pochyla, obie jednakowej wysokości
i mające wspólny wierzchotek. Na prostopadłej, ponad tym wierzchołkiem
znaleźć punkt, z którego by ciało spadało wzdłuż prostopadłej, a dalej
wzdłuż równi, tak samo długo, jak wzdłuż prostopadlej spuszczonej z jej
wierzchołka.
(...)
Zadanie XIII. Podanie XXXIV
Niech będą prostopadła i równia pochyłla, mające wspólny
wierzchołek. Szukany jest punkt położony wyżej na prostopadłej, z
którego by ciało spadające i biegnące dalej wzdłuż równi pochyłej,
wykonywało te ruchy w tym samym czasie, co i spadek po samej równi z
jej wierzchołka.
(...)
Zadanie XIV. Podanie
XXXV
Dane są prostopadła i od jej spodu równia pochyła; oznaczyć na tej
ostatniej punkt, do którego przebyta będzie wzdłuż samej równi droga
w tym samym czasie co i droga wzdłuż prostopadłej i równi.
(...)
Twierdzenie XXII. Podanie XXXVI
Jeżeli z najniższego punktu koła, stojącego na poziomie,
poprowadzimy równię pochylą podpierającą mniej niż ćwierć koła i
jeżeli z końców tej równi poprowadzimy dwie równie do jakiegokolwiek
punktu łuku podpartego, to spadek wzdłuż tych dwóch równi trwać będzie
krócej aniżeli wzdłuż równi pierwszej, a także krócej niż wzdłuż samej
niższej z dwóch równi.
(...)
Scholium
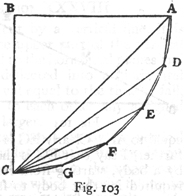 Z poprzedniego wywnioskować można, że najszybszy ruch od jednego
punktu do drugiego odbywa się nie wzdłuż najkrótszej linii tj. prostej,
ale po łuku koła. Bo, dzieląc ćwierć koła (rys. 103) BAEC,
której bok BC jest prostopadły do poziomu, to jest łuk AC, na dowolną liczbę
części równych AD, DE, EF, FG, GC, prowadząc z C linie proste do punktów
A, D, E, F, G, i łącząc je liniami AD, DE, EF, VG,
GC, widzimy, że ruch wzdłuż ADC jest prędszy niż wzdłuż AC albo wzdłuż
DC po wyjściu ze spoczynku w D, ale z A będzie DC przebyte prędzej
niż obie drogi ADC, podobnie po dwóch DEC po wyjściu ze spoczynku w A
spadek odbywa się prędzej niż po samym DC. Spadek więc po trzech ADEC
będzie szybszy niż po dwóch ADC. Podobnie spadek w dalszym ciągu ADE
będzie szybszy wzdłuż dwóch EFC niż wzdłuż samego EC. Więc wzdłuż
czterech ADEFC szybszy niż wzdłuż trzech ADEC. A że wzdłuż dwóch FGC, w dalszym
ciągu spadku wzdłuż ADEF, spadek będzie szybszy niż wzdłuż FC, więc
wzdłuż pięciu ADEFGC szybszy niż wzdłuż czterech ADEFC. Im więcej
przeto wielobok wpisany zbliża się do obwodu koła, tym szybciej odbywa
się ruch między A i C.
Z poprzedniego wywnioskować można, że najszybszy ruch od jednego
punktu do drugiego odbywa się nie wzdłuż najkrótszej linii tj. prostej,
ale po łuku koła. Bo, dzieląc ćwierć koła (rys. 103) BAEC,
której bok BC jest prostopadły do poziomu, to jest łuk AC, na dowolną liczbę
części równych AD, DE, EF, FG, GC, prowadząc z C linie proste do punktów
A, D, E, F, G, i łącząc je liniami AD, DE, EF, VG,
GC, widzimy, że ruch wzdłuż ADC jest prędszy niż wzdłuż AC albo wzdłuż
DC po wyjściu ze spoczynku w D, ale z A będzie DC przebyte prędzej
niż obie drogi ADC, podobnie po dwóch DEC po wyjściu ze spoczynku w A
spadek odbywa się prędzej niż po samym DC. Spadek więc po trzech ADEC
będzie szybszy niż po dwóch ADC. Podobnie spadek w dalszym ciągu ADE
będzie szybszy wzdłuż dwóch EFC niż wzdłuż samego EC. Więc wzdłuż
czterech ADEFC szybszy niż wzdłuż trzech ADEC. A że wzdłuż dwóch FGC, w dalszym
ciągu spadku wzdłuż ADEF, spadek będzie szybszy niż wzdłuż FC, więc
wzdłuż pięciu ADEFGC szybszy niż wzdłuż czterech ADEFC. Im więcej
przeto wielobok wpisany zbliża się do obwodu koła, tym szybciej odbywa
się ruch między A i C.
Co zaś dowiedziono dla ćwiercianu, to odnosi się także w kole i do
mniejszych łuków i taki jest wywód.
[Ten "dowód" Galileusza jest błędny - ale nie miał on
narzędzi niezbędnych do rozwiązania tego problemu. Rozwiązanie podał
wiek później J. Bernoulli].
Zadanie XV. Podanie
XXXVII
Mając daną prostopadłą i równię pochyłą tej samej wysokości, oznaczyć
położenie odcinka równi tej samej długości co i prostopadła, po
którym by ruch odbywał się w tym samym czasie, co i wzdłuż prostopadłej.
(...)
Wniosek
Wynika stąd, że szukany odcinek leży na równi między częściami górną
i dolną, które są przebywane w czasach
równych.
Zadanie XVI. Podanie
XXXVIII
Dane są dwie
płaszczyzny poziome przecięte przez prostopadłą;
znaleźć na tej ostatniej punkt taki, z którego by ciało spadające
najpierw prostopadle, a następnie poruszające się po danych
płaszczyznach, przebywało wzdłuż tych ostatnich, w czasach równych
czasowi spadku po prostopadłej, drogi pozostające jedna do drugiej w
danym stosunku.
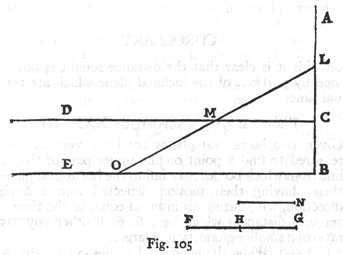 Niech będą (rys. 105) płaszczyzny poziome CD, BE, przecięte
prostopadłą ACB i dany stosunek drogi krótszej do dłuższej N do FG. Na
prostopadłej w górze ma być oznaczony punkt, z którego by spadające
ciało, zwrócone na CD, przebywało w czasie równym czasowi spadku drogę,
tak się mającą do drogi przebywanej przez inne ciało spadające z tegoż
samego punktu i zwrócone na płaszczyznę BE w czasie równym swemu czasowi
spadku, jak N do FG. Połóżmy GH równe N i jak FH do MG tak niech się ma
BC do CL. Twierdzę, że L będzie szukanym punktem w górze prostopadłej.
Odetnijmy CM=2CL, poprowadźmy LM, przecinającą płaszczyznę EB w O, to
będzie także BO=2BL. A ponieważ jak FH do HG, tak się ma BC do CL, to
także jak HG czyli N do GF będzie CL do LB albo CM do BO. Że zaś CM=2CL,
to CM będzie drogą, którą ciało, wyszedłszy z L, po spadku wzdłuż LC,
przebiegnie na płaszczyźnie CD; i dla tej samej przyczyny BO będzie
drogą, przebytą po spadku wzdłuż LB, w czasie równym czasowi spadku
po LB; że zaś BO jest równe 2BL, więc zadanie jest rozwiązane.
Niech będą (rys. 105) płaszczyzny poziome CD, BE, przecięte
prostopadłą ACB i dany stosunek drogi krótszej do dłuższej N do FG. Na
prostopadłej w górze ma być oznaczony punkt, z którego by spadające
ciało, zwrócone na CD, przebywało w czasie równym czasowi spadku drogę,
tak się mającą do drogi przebywanej przez inne ciało spadające z tegoż
samego punktu i zwrócone na płaszczyznę BE w czasie równym swemu czasowi
spadku, jak N do FG. Połóżmy GH równe N i jak FH do MG tak niech się ma
BC do CL. Twierdzę, że L będzie szukanym punktem w górze prostopadłej.
Odetnijmy CM=2CL, poprowadźmy LM, przecinającą płaszczyznę EB w O, to
będzie także BO=2BL. A ponieważ jak FH do HG, tak się ma BC do CL, to
także jak HG czyli N do GF będzie CL do LB albo CM do BO. Że zaś CM=2CL,
to CM będzie drogą, którą ciało, wyszedłszy z L, po spadku wzdłuż LC,
przebiegnie na płaszczyźnie CD; i dla tej samej przyczyny BO będzie
drogą, przebytą po spadku wzdłuż LB, w czasie równym czasowi spadku
po LB; że zaś BO jest równe 2BL, więc zadanie jest rozwiązane.
SAGREDO: Istotnie zdaje mi się, że przyznać trzeba naszemu
akademikowi, że on bez przechwałki przypisywać sobie może zasługę
utworzenia nowej nauki o bardzo starym przedmiocie. A widząc, jak on
szczęśliwie i zręcznie z jednej prostej zasady wywodzi dowodzenia tylu
twierdzeń, muszę niemniej podziwiać, że rzeczy te
pozostawiały nietkniętymi przez Archimedesa, Apolloniusza, Euklidesa i
tylu innych matematyków i filozofów znakomitych, a zwłaszcza, że o tym
ruchu znajduje się napisanych wiele grubych tomów.
SALVIATI: O ruchu znaleźć trochę można w odnośnym fragmencie
Euklidesa, lecz nie można odkryć śladu, jaką szedł drogą, aby odkryć
stosunek przyspieszenia i jego zmiany przy różnych nachyleniach.
Twierdzić też można, że teraz dopiero otwarty został dostęp do nowej
metody, umożliwiającej nieskończenie mnóstwo ważnych badań, które w
przyszłości inne umysły będą mogły przeprowadzać.
SAGREDO: Sądzę istotnie, że równie jak pewne własności koła, które
jako przykłady dowiedzione są w trzeciej księdze Euklidesa, stanowią
wstęp do niezliczonej liczby innych, więcej ukrytych, tak samo te, w
krótkiej rozprawie wywiedzione twierdzenia, skoro się znajdą w ręku
innych myślących badaczy, torować będą drogę do coraz to nowych
pomysłów i prawdopodobnie z czasem takie gruntowne badanie przedmiotu
rozciągnie się na wszystkie inne zakresy przyrody.
Dzień dzisiejszy był długi i dość pracowity, lecz więcej mnie
zadowoliły same podania aniżeli ich dowodzenia i sądzę, że aby je
dobrze zrozumieć, poświęcić trzeba każdemu więcej niż godzinę: odkładając tę pracę do czasu spokojnego, poproszę Waszmość o
pozostawienie mi książki, po rozpatrzeniu pozostałej jej części
odnoszącej się do ruchu pocisków; co, jeżeli pozwolicie, będzie mieć
miejsce w dniu następnym.
SALVIATI: Nie omieszkam spotkać się z Waszmościami.
Koniec dnia trzeciego.
DZIEŃ CZWARTY
SALVIATI: Otóż i p. Simplicio przychodzi w porę, abyśmy bez
odkładania mogli przejść do ruchu, a taki jest tekst naszego autora.
O RUCHU POCISKÓW
Rozważaliśmy dotąd ruch jednostajny, oraz naturalnie przyspieszony
wzdłuż równi pochyłych. W dalszym ciągu zajmę się niektórymi zjawiskami
i wskazówkami naukowymi ściśle dowiedzionymi, dotyczącymi ciał w ruchu
złożonym z jednostajnego i naturalnie przyspieszonego; tego rodzaju
bowiem jest ruch pocisków i w ten sposób powstaje.
Jeżeli ciało bez żadnej przeszkody porusza się na płaszczyźnie
poziomej, to ze wszystkiego, co poprzednio obszernie zostało wyłożone,
wynika, że ten ruch jest jednostajny i nieustannie trwający, przy
rozciąganiu się płaszczyzny do nieskończoności; gdy zaś płaszczyzna
jest ograniczona, a poruszające się na niej ciało ciężkie, to ono,
doszedłszy do brzegu płaszczyzny, poruszać się będzie dalej, a do
pierwotnego, jednostajnego, nieginącego ruchu dochodzi ruch wywołany
przez ciężkość i wytwarza się ruch złożony, który nazywam pociskowym i
który się składa z jednostajnego poziomego i z jednostajnie
przyspieszonego. Wywiedziemy tu niektóre właściwości tego ruchu, z
których pierwsza jest następująca.
Twierdzenie I. Podanie I
Pocisk w swym ruchu złożonym z jednostajnego poziomego i naturalnie
przyspieszonego z góry na dół, opisuje połowę paraboli.
SAGREDO: Musimy tu, panie Salviati, tak dla mnie jak i dla p.
Simplicia, nieco się zatrzymać, gdyż nie jestem tak daleko posunięty w
geometrii, abym studiował Apollonosa, który, o ile wiem, pisał o tych
parabolach i innych przecięciach stożkowych, nie sądzę zaś, abyśmy
mogli bez tych wiadomości rozumieć dowodzenia podań, jakie mają
nastąpić. A ponieważ, zaraz w pierwszym twierdzeniu, autor ma nam
dowieść, że linia, jaką opisuje pocisk, jest parabolą, to zdaje mi się,
że najpierw zająć się trzeba tą krzywą, gruntownie ją poznać i choćby
nie wszystkie wywiedzione przez Apollonosa jej własności, to
przynajmniej te z nich przypomnieć, na których opierać się będą dalsze
rozważania.
SALVIATI: Waszmość zbyt się poniża, żądając podania na nowo
wiadomości, które niedawno przyjmowaliście jako dobrze znane: wtedy,
powiadam, gdy przy rozważaniu wytrzymałości posługiwaliśmy się już
pewnem podaniem Apolloniosa, co nie robiło nam żadnej trudności.
SAGREDO: Być może znałem je przypadkowo, lub przyjmowałem jako
znane, dopókąd było potrzebne podczas rozważania; tu wszakże, gdy mamy
się zapoznać z wieloma twierdzeniami, dotyczącymi tych linii, nie
możemy żałować czasu i trudu.
SIMPLICIO: Co się mnie tyczy, to chociaż, jak sądzę, p. Sagredo będzie
dobrze zaopatrzony, mnie zatrzymują dawne przeszkody, bo jakkolwiek nasi
filozofowie traktowali już o ruchu pocisków, to jednak nie przypominam
sobie, aby określali linie w tym ruchu opisywane inaczej, jak ogólnie
jako linie krzywe, z wyjątkiem tylko spadku po prostopadłej. Toteż
jeżeli ta szczypta geometrii, której tu i owdzie w ciągu naszych rozmów
nauczyłem się z Euklidesa, nie wystarczy do zrozumienia dalszych
dowodzeń, zmuszony będę przyjmować twierdzenia na wiarę, nie sięgając do
ich głębi.
SALVIATI: Pragnę też zbudzić w Was wdzięczność dla naszego autora,
który mi pozwolił rzucić okiem na swoją pracę, a ponieważ nie miałem
wtedy pod ręką ksiąg Apolloniosa, wyjaśnił mi dwie główne własności
paraboli, bez żadnych wstępnych studiów i na tych własnościach oprzemy
się w naszem rozważaniu; dowiedzione zostały te własności przez
Apolloniosa, ale między wieloma innymi, których poznawanie zabrałoby
nam zbyt wiele czasu; ja zaś pragnąłbym skrócić tę drogę, wyciągając
pierwszą własność po prostu z samego powstawania paraboli i wiążąc z nią
bezpośrednio dowodzenie drugiej własności. Przejdziemy więc najpierw do
pierwszej własności.
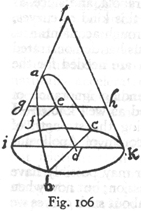 Wyobraźmy sobie (rys. 106)
stożek prosty z podstawą kołową
IBKC i wierzchołkiem w punkcie L, który przecięty płaszczyzną
równoległą do boku LK daje przecięcie BAC zwane parabolą; jej podstawa
BC przecina pod kątem prostym średnicę IK koła IBKC i niech będzie oś
paraboli AD równoległa do boku LK; weźmy jakikolwiek punkt F na linii
BFA i poprowadźmy prostą FE, równoległą do BD. Twierdzę, że kwadrat z BD
ma się do kwadratu z FE, jak oś DA do odcinka AE. Wyobraźmy sobie przez
punkt E przeprowadzoną płaszczyznę, równoległą do koła IBKC, to ta
przetnie stożek według koła o średnicy GEH. A ponieważ BD jest
prostopadła do IK, średnicy koła IBK, to kwadrat z BD jest równy
prostokątowi o bokach ID, DK. Tak samo będzie na kole górnym, przechodzącym przez punkty G, F, H, kwadrat z linii FE równy
prostokątowi o bokach GE, EH. Więc kwadraty z BD i FE mają się do siebie
jak prostokąt IDK do prostokąta GEH. A ponieważ linia ED jest
równoległa do HK, to będzie EH równe DK, gdyż są równoległe; a że
prostokąt IDK ma się do prostokąta GEH jak ID do GE, czyli jak DA do AE;
więc prostokąt IDK ma się do prostokąta GEH, jak kwadrat z BD do
kwadratu z FE, albo jak oś DA do odcinka AE, c.b.d.d.
Wyobraźmy sobie (rys. 106)
stożek prosty z podstawą kołową
IBKC i wierzchołkiem w punkcie L, który przecięty płaszczyzną
równoległą do boku LK daje przecięcie BAC zwane parabolą; jej podstawa
BC przecina pod kątem prostym średnicę IK koła IBKC i niech będzie oś
paraboli AD równoległa do boku LK; weźmy jakikolwiek punkt F na linii
BFA i poprowadźmy prostą FE, równoległą do BD. Twierdzę, że kwadrat z BD
ma się do kwadratu z FE, jak oś DA do odcinka AE. Wyobraźmy sobie przez
punkt E przeprowadzoną płaszczyznę, równoległą do koła IBKC, to ta
przetnie stożek według koła o średnicy GEH. A ponieważ BD jest
prostopadła do IK, średnicy koła IBK, to kwadrat z BD jest równy
prostokątowi o bokach ID, DK. Tak samo będzie na kole górnym, przechodzącym przez punkty G, F, H, kwadrat z linii FE równy
prostokątowi o bokach GE, EH. Więc kwadraty z BD i FE mają się do siebie
jak prostokąt IDK do prostokąta GEH. A ponieważ linia ED jest
równoległa do HK, to będzie EH równe DK, gdyż są równoległe; a że
prostokąt IDK ma się do prostokąta GEH jak ID do GE, czyli jak DA do AE;
więc prostokąt IDK ma się do prostokąta GEH, jak kwadrat z BD do
kwadratu z FE, albo jak oś DA do odcinka AE, c.b.d.d.
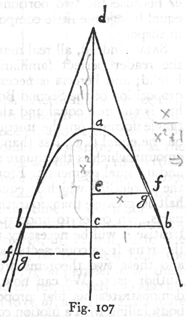
Drugie podanie, potrzebne w naszem rozważaniu, jest następujące.
Nakreślmy parabolę (rys. 107) i przedłużmy jej oś CA na zewnątrz
do D, poprowadźmy przez jakikolwiek jej punkt B linię BC równoległą do
podstawy paraboli i odetnijmy DA równe osi CA. Twierdzę, że linia
prosta, poprowadzona przez punkty D, B, nie będzie przecinała paraboli,
lecz tylko dotykać się jej będzie w tym samym punkcie B. Albowiem,
jeżeli to jest możliwe, to ona przetnie parabolę wyżej, a jej
przedłużenie niżej. Weźmy więc na niej jakikolwiek punkt G i poprowadźmy
prostą FGE. Ponieważ kwadrat z FE jest większy od kwadratu z GE, to
stosunek kwadratu FE do kwadratu z BC będzie większy od stosunku
kwadratu GE do tegoż kwadratu z BC. A ponieważ, według twierdzenia
poprzedniego, kwadrat z FE ma się do kwadratu z BC, jak EA do AC, to
stosunek EA do AC będzie większy od stosunku kwadratu z GE do kwadratu
z BC albo kwadratu z ED do kwadratu DC (bo w trójkącie DGE tak się ma
GE do równoległej BC, jak ED do DC). Ale linia EA tak się ma do AC albo
do AD, jak cztery prostokąty EAD do czterech kwadratów z AD, czyli do
kwadratu z CD (który jest równy czterem kwadratom z AD); mamy więc, że
stosunek czterech prostokątów EAD do kwadratu z CD jest większy od
stosunku kwadratu z ED do kwadratu z DC; byłyby więc cztery prostokąty
EAD większe od kwadratu ED, co jest nieprawdziwe, gdyż one są mniejsze;
a to dlatego, że części EA i AD linii ED nie są równe. Więc linia DB
dotyka paraboli w B, ale jej nie przecina, c.b.d.d.
SIMPLICIO: Wywody swe prowadzacie zbyt okazale; i przyjmujecie
zawsze, o ile mi się zdaje, że wszystkie podania Euklidesa są mi równie
dobrze znane, jak jego pierwsze aksjomaty, a tak nie jest. I tak
dopiero co usłyszałem, że cztery prostokąty EAD są mniejsze od kwadratu z
DE, dlatego, że części EA, AD linii ED nie są równe, co mnie nie
zaspokaja i o czym powątpiewam.
SALVIATI: Istotnie wszyscy poważniejsi matematycy przyjmują, że
czytelnikowi co najmniej Elementy Euklidesa dobrze są znane; panu zaś
wystarczy przypomnieć, że jeżeli linia podzielona zostanie raz na części
równe, a drugi raz na nierówne, to prostokąt z części nierównych jest
mniejszy od prostokąta z części równych (czyli kwadratu z połowy) o
kwadrat z odległości między punktami podziału. Wynika stąd, że kwadrat
z całości, obejmujący cztery kwadraty z połowy, jest większy od
czterech prostokątów z części nierównych. Dowiedzione dwa twierdzenia z
Elementów przecięć stożkowych należy mieć w pamięci, dla
zrozumienia dalszego ciągu niniejszej rozprawy, bo na nich tylko opiera
się autor. Teraz więc wrócić możemy do tekstu, aby zobaczyć, w jaki
sposób dowiedzione tam jest pierwsze twierdzenie, wykazujące, że linia
opisana przez pocisk w ruchu złożonym z jednostajnego poziomego i
naturalnego, spadającego jest połową paraboli.
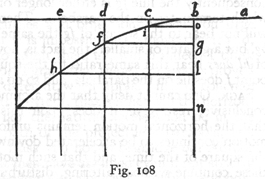 Wyobraźmy sobie (rys. 108) linię albo płaszczyznę poziomą
AB, wysoko umieszczoną, po której ciało od A do B jednostajnie się
porusza; po usunięciu zagrody w B, ciało, skutkiem swej ciężkości
poddane zostaje naturalnemu spadkowi wzdłuż pionowej BN. Przedłużmy AB w
linii prostej do E i odcinajmy na BE równe części upływającego czasu
BC, CD, DE, a z punktów C, D, E, poprowadźmy równoległe do poziomej BN:
na pierwszej z nich odetnijmy jakąkolwiek długość CI, na następnej
cztery razy większą DF, potem dziewięć razy większą EH i tak dalej w
stosunku do kwadratów z CB, DB, EB, czyli w podwójnym stosunku tych
długości. Bo jeżeli przyjmujemy, że do ruchu jednostajnego od B do C,
dochodzi spadek pionowy na długości Cl, to ciało po upływie czasu BC
znajdzie się w punkcie I. Dalej w ciągu czasu DB, czyli zdwojonego BC,
będzie droga przebyta w spadku równa czterokrotnemu CI: bo w pierwszym
traktacie dowiedziono, że przy ruchu jednostajnie przyspieszonym drogi
przebyte mają się do siebie jak kwadraty z czasów. Podobnież będzie
droga EH, przebyta w spadku, w ciągu czasu BE, równa dziewięciokrotnemu
CI, bo Eli, DF, CI mają się do siebie, jak kwadraty z linij EB, DB, CB.
Jeżeli przez punkty I, F, H, poprowadzimy proste I0, FG, HL, równoległe
do EB, to będą linie HL, FG, I0 równe liniom EB, DB, CB; równie jak BO,
BG, BL są równe CI, DF, EH. Więc kwadrat z HL ma się do kwadratu FG jak
linia LB do BG; a kwadrat z FG do kwadratu z I0 jak GB do BO. Punkty
więc I, F, H, leżą na jednej i tej samej linii parabolicznej. Podobnież
biorąc inne jakiekolwiek wielkości, odpowiadające równym częściom
czasu, można by dowieść, że punkty, do których dochodzi w tych czasach
pocisk, leżą na jednej i tej samej linii parabolicznej, c.b.d.d.
Wyobraźmy sobie (rys. 108) linię albo płaszczyznę poziomą
AB, wysoko umieszczoną, po której ciało od A do B jednostajnie się
porusza; po usunięciu zagrody w B, ciało, skutkiem swej ciężkości
poddane zostaje naturalnemu spadkowi wzdłuż pionowej BN. Przedłużmy AB w
linii prostej do E i odcinajmy na BE równe części upływającego czasu
BC, CD, DE, a z punktów C, D, E, poprowadźmy równoległe do poziomej BN:
na pierwszej z nich odetnijmy jakąkolwiek długość CI, na następnej
cztery razy większą DF, potem dziewięć razy większą EH i tak dalej w
stosunku do kwadratów z CB, DB, EB, czyli w podwójnym stosunku tych
długości. Bo jeżeli przyjmujemy, że do ruchu jednostajnego od B do C,
dochodzi spadek pionowy na długości Cl, to ciało po upływie czasu BC
znajdzie się w punkcie I. Dalej w ciągu czasu DB, czyli zdwojonego BC,
będzie droga przebyta w spadku równa czterokrotnemu CI: bo w pierwszym
traktacie dowiedziono, że przy ruchu jednostajnie przyspieszonym drogi
przebyte mają się do siebie jak kwadraty z czasów. Podobnież będzie
droga EH, przebyta w spadku, w ciągu czasu BE, równa dziewięciokrotnemu
CI, bo Eli, DF, CI mają się do siebie, jak kwadraty z linij EB, DB, CB.
Jeżeli przez punkty I, F, H, poprowadzimy proste I0, FG, HL, równoległe
do EB, to będą linie HL, FG, I0 równe liniom EB, DB, CB; równie jak BO,
BG, BL są równe CI, DF, EH. Więc kwadrat z HL ma się do kwadratu FG jak
linia LB do BG; a kwadrat z FG do kwadratu z I0 jak GB do BO. Punkty
więc I, F, H, leżą na jednej i tej samej linii parabolicznej. Podobnież
biorąc inne jakiekolwiek wielkości, odpowiadające równym częściom
czasu, można by dowieść, że punkty, do których dochodzi w tych czasach
pocisk, leżą na jednej i tej samej linii parabolicznej, c.b.d.d.
SALVIATI: Wniosek ten otrzymany został przez odwrócenie poprzednio
dowiedzionego twierdzenia, gdyż jeżeli przez punkty B, H,
przeprowadzimy parabolę, a punkty F, I nie będą leżały na tej krzywej,
lecz na zewnątrz lub na wewnątrz; to FG będzie mniejsze lub większe od
linii dochodzącej do paraboli i kwadraty z HL i FG mieć będą do siebie
większy lub mniejszy stosunek od linii LB i BG, tymczasem kwadrat z HL
ma zawsze ten właśnie stosunek do kwadratu z FG; więc punkt F leży na
paraboli i tak samo wszystkie inne pukty.
SAGREDO: Nie mogę zaprzeczyć, że rozważanie to jest nowe, pomysłowe i
konkludujące; opiera się ono na tym mianowicie założeniu, że ruch
poprzeczny utrzymuje się zawsze jednostajny, że ruch naturalnie
przyspieszony jest proporcjonalny do kwadratów z czasu i że te ruchy i
ich prędkości mieszają się ale sobie nie przeszkadzają, nie zmieniają
się i nie opóźniają, tak że linia rzutu, przy dalszym ruchu, nie zmienia
swej natury; to zaś nie wydaje mi się możliwe. Bo ponieważ oś naszej
paraboli, wzdłuż której zakładamy, że się odbywa ruch naturalny ciężarów,
jest prostopadłą do poziomu, więc dochodzi do środka ziemi, parabola zaś
oddala się wciąż od swej osi, więc pocisk nie doszedłby nigdy do środka
ziemi, a gdyby zaś doszedł, co wydaje się konieczne, to musiałaby
linia rzutu przerodzić się na inną, różną od parabolicznej.
[Tu Galileusz powtórzył błąd, jaki wcześniej pojawił
się w I dniu Dialogu.]
SIMPLICIO: Do tej trudności dołączyć muszę inne jeszcze: jedna z nich
polega na tym naszym przypuszczeniu, że płaszczyzna pozioma, która ani
się nie podnosi ani nie obniża, jest linią prostą, tak jakby jej części
były wszędzie jednakowo oddalone od środka ziemi, co przecież nie jest
prawdą; bo postępując od środka płaszczyzny do jej końców, coraz więcej
oddalamy się od środka ziemi, a więc płaszczyzna wciąż się podnosi;
wynika stąd, że na takiej płaszczyźnie ruch nie może trwać wiecznie i nie
może na żadnej jej części utrzymywać się jednostajnym, ale wciąż się
zwalnia. Nadto uważam za niemożliwe, aby można było unikać oporu ośrodka
i aby się zachowywała stałość ruchu poprzecznego, jak i praca
przyspieszenia ciał spadających. Przy tych wszystkich trudnościach
wydaje się bardzo nieprawdopodobne, aby to, co było dowiedzione,
wychodząc z tak niepewnych założeń, mogło być sprawdzone
doświadczeniami.
SALVIATI: Wszystkie postawione trudności i żądania tak są
uzasadnione, że pominięcie ich uważam za niemożliwe; toteż przyjmuję je
wszystkie i sądzę, że i nasz autor to samo by uczynił. Godzę się nawet
na to, że nasz abstrakcyjnie wyciągnięty wniosek zmieni się w
rzeczywistość i okaże się do tego stopnia mylny, że ani ruch poprzeczny
nie jest jednostajny, ani przyspieszenie ruchu naturalnego nie ma
przyjmowanej proporcji, ani linia rzutu nie jest parabolą i.t.d. Lecz w
zamian za to proszę, abyście nie kwestionowali naszemu autorowi tego,
co przyjmowali inni najznakomitsi mężowie, jakkolwiek to było fałszywe.
A sama już powaga Archimedesa może każdego uspokoić; przyjął on w swej
mechanice, przy pierwszej kwadraturze paraboli, jako pewnik, że drąg
wagi jest linią prostą, której wszystkie punkty są jednakowo oddalone od
wspólnego środka ciał ważkich, a sznury, na których zawieszone są
ciężary, są do siebie równoległe. Tę licencję przyzna nam każdy, bo
nasze narzędzia i odległości, z jakimi mamy do czynienia, są tak małe
w porównaniu z naszem wielkiem oddaleniem od środka ziemi, że możemy
przyjmować bardzo małą cząstkę łuku wielkiego koła za linię prostą, a
dwie prostopadłe z jej końców spuszczone za równoległe do siebie.
Gdybyśmy chcieli uwzględniać przy doświadczeniach takie małe wielkości,
musielibyśmy zacząć od poprawiania architektów, którzy ze swym pionem
przyjmują najwyższe wieże wzniesione między liniami równolegtemi.
Dodam, że moglibyśmy również powiedzieć, iż Archimedes i inni
przyjmowali w swych rozważaniach, że są nieskończenie oddaleni od środka
ziemi, a w tym przypadku ich podania nie byłyby błędne; i dlatego wnioskowali z absolutną ścisłością.
Jeżeli więc chcemy
stosować w skończonej odległości dowiedzione wnioski do odległości
nieskończenie wielkich, musimy od prawdziwie dowiedzionego odciągnąć
to, co z powodu nie nieskończonej odległości jest do uwzględnienia;
chociaż zawsze odległość jest jeszcze bardzo wielka w porównaniu z
małością naszych urządzeń, z których największym jest
nośność pocisków
przy wystrzałach, zwłaszcza armatnich; jakkolwiek ta ostatnia jest
wielką, nie przenosi jednak czterech mil, podczas gdy odlegli jesteśmy
od środka ziemi na tyleż tysięcy mil; a jeżeli tę nośność odmierzymy na
powierzchni ziemi, to linia paraboliczna nieznacznie tylko się zmieni, w
rzeczywistości zaś tak się skieruje, że przejdzie przez środek ziemi.
Następnie, co do przeszkód, pochodzących z oporu ośrodka, to te są
znaczniejsze a z powodu swej wielkiej różnorodności niemożliwe do
zawarcia w pewnych prawidłach ścisłych; bo, dopókąd bierzemy tylko pod
uwagę opór powietrza, to ten przeszkadza wszystkim ruchom w sposób
nieskończenie rozmaity, stosownie do nieskończenie różnych zmian
kształtów, ciężarów i prędkości ciał. Co do prędkości, to im ona jest
większa, tym większy będzie także opór powietrza, które tym więcej
przeszkadza, im ciało jest lżejsze; tak że jakkolwiek ciężar powinien by spadać z przyspieszeniem
proporcjonalnym do kwadratów z czasów, to jednak tylko bardzo
ciężkie
ciała, spadające ze znacznej wysokości doznają od powietrza takiego
oporu, że ten może pokonać w zupełności przyspieszenie i uczynić ruch
jednostajnym; co następuje tym prędzej i na tym mniejszej wysokości, im
ciało jest lżejsze. Również i ruch poziomy, który po usunięciu
wszystkich przeszkód, winien by być jednostajny i wiecznie trwający,
będzie skutkiem oporu powietrza hamowany i w końcu
zatrzymany, a to tym prędzej, im ciało będzie lżejsze.
Dla tych
wszystkich nieskończenie różnych przypadków, ciężkości, prędkości i
kształtu nic można podać żadnej ścisłej teorii.
Trzeba je więc
abstrahować, aby móc naukowo traktować ten przedmiot, a wnioskami
znalezionymi i dowiedzionymi bez brania pod uwagę przeszkód, posługiwać
się w tych granicach, jakie wskaże doświadczenie. A nie mały stąd
będzie pożytek, bo tworzywo i kształt tak zostaną dobrane, aby opór
ośrodka był możliwie mały, mianowicie wybrane będą ciała najcięższe i
okrągłe: przy tym drogi i prędkości nie będą zbyt wielkie, abyśmy nie
mogli dokładnie ich zmierzyć. Przeciwnie, pociski, których używaliśmy,
były z materii ciężkiej i okrągłego kształtu, a jeżeli z materii
lżejszej, to miały kształt walców, jak strzały rzucone z procy lub łuku,
a jednak odchylenia ich dróg od linii parabolicznej były nieznaczne.
Nawet (i tu wziąć pragnę nieco więcej swobody) małość tych odchyleń była
taka, że zewnętrzne działania poboczne, między którymi najważniejszy
jest opór ośrodka, nie mogły być zauważone przy naszych
doświadczeniach, co mogę uwidocznić na dwóch następujących. Wezmę pod
uwagę ruchy w powietrzu, gdyż takie były przeważnie te, o których
mówiliśmy, przy tych ruchach zaś powietrze w dwojaki sposób wywiera
działanie. Najpierw więcej opóźnia ruch ciał lekkich aniżeli ciężkich.
Następnie przy ruchu jednego i tegoż samego ciała większy stawia opór
przy większej prędkości, aniżeli przy mniejszej. Co do pierwszego,
doświadczenie wykazało, że dwie równie wielkie kule, z których jedna
jest 10 do 12 razy cięższa od drugiej, spadając z wysokości 150 do 200
łokci, dochodzą do ziemi z bardzo małą różnicą prędkości, co nas
upewnia, że obie doznają bardzo małego oporu powietrza; bo gdyby kula
ołowiana, zaczynająca spadać w tym samym momencie co i drewniana, mniej
była od niej opóźniana, to musiałaby przy tak znacznej wysokości
dochodzić do ziemi wyprzedzając drewnianą, gdyż jest 10 razy cięższą;
to jednak się nie zdarza, bo wyprzedzanie nie wynosi ani setnej części
całej wysokości. Pomiędzy zaś kulą ołowianą a kamienną, ważącą zaledwie
trzecią część lub połowę pierwszej, różnica w dojściu do ziemi zaledwie
mogła być zauważoną. A ponieważ impet, nabyty przez kulę ołowianą przy
spadku z wysokości 200 łokci, (który jest taki, że pozwoliłby jej
przebiec w dalszym ciągu spadku, w tym
samym czasie ruchem jednostajnym, 400 łokci) jest dość znaczny w
porównaniu z prędkościami, które łukiem lub innymi maszynami nadawać
możemy naszym pociskom (z wyjątkiem impetu, jaki daje broń palna), to
zapewne niewiele zbłądzimy, jeżeli twierdzenie dowiedzione bez
uwzględniania oporu ośrodka, poczytamy za absolutnie prawdziwe.
Co do drugiego z wymienionych punktów, to
opór, jakiego jedno i toż samo ciało doznaje od powietrza, gdy się
porusza z wielką prędkością, nie jest znacznie większy od oporu jakiego
doznaje przy wolniejszym ruchu, co może być stwierdzone następującym doświadczeniem. Na dwóch jednakowo
długich nitkach, 4-o lub 5-cio łokciowych zawieszamy dwie kulki ołowiane
i wyprowadzamy obie z położenia pionowego, podnosząc jedną na 80 lub
więcej stopni a drugą na 4 lub 5; puszczone swobodnie, opisują,
spadając i przekraczając pionową, jedna wielkie łuki 160, 150, 140
stopni, powoli się zmniejszające, a druga łuki małe 10, 8, 6 itd.,
zmniejszające się jeszcze wolniej. Twierdzę więc najpierw, że łuki 180,
160 itd. opisywane będą w tych samych czasach, co i małe 10, 8, itd. A
ponieważ oczywiście prędkość pierwszej kulki jest 16 i 18 razy większa
niż drugiej, a przy większej prędkości większy być musi opór powietrza
niż przy mniejszej, to wahań winnoby być mniej przy wielkich łukach 180,
160 stopni itd. niż przy małych 10, 8, 4 albo 2 i 1; ale temu przeczy
doświadczenie; bo gdy dwaj towarzysze wzięli się do liczenia wahań,
jeden wielkich a drugi małych, to przekonali się, licząc nie tylko
dziesiątki ale i setki, że nie różnili się ani o jedno wahnięcie.
Doświadczenie to stwierdza jednocześnie oba twierdzenia, a mianowicie,
że wielkie i małe wahania odbywają się wszystkie w czasach równych i że
opór powietrza nie działa więcej opóźniająco przy ruchach prędkich niż
przy powolnych, wbrew temu, co się nam przedtem wydawało i co mylnie
przyjmowaliśmy.
[Ta "relacja" z przebiegu eksperymentów jest
całkowicie błędna.
Czy Galileusz kiedykolwiek takie eksperymenty przeprowadzał?]
SAGREDO: Ale ponieważ nie można przeczyć, że powietrze stawia opór i
jednej i drugiej kulce, bo przecież obie zwalniają ruch i w końcu się
zatrzymują, należy więc powiedzieć, że opóźnienia następują przy obu
kulkach w tym samym stosunku. Ale w jakim? Jeżeli w jednym przypadku
opór jest większy niż w drugim, od czegóż to może zależeć, jak nie od
tego, że raz był wywołany większą prędkością, a drugi raz mniejszą? I
ponieważ tak się rzecz ma, to właśnie
ta ilość prędkości jest przyczyną, a zarazem miarą oporu. Będą więc
wszystkie ruchy, małe i wielkie, opóźniane i hamowane w tym samym
stosunku; uwaga ta nie wydaje mi się zbyteczna.
SALVIATI: Można by także i w tym drugim przypadku wnioskować, że
odchylenia od wniosków, dowiedzionych niezależnie od okoliczności
zewnętrznych mają tylko małe znaczenie, odnośnie do ruchów z wielką
prędkością, którymi najwięcej przyjdzie się tu zajmować, a także
odnośnie do odległości, które są bardzo małe w porównaniu z wielkością
promienia i kół wielkich globu ziemskiego.
SIMPLICIO: Pragnąłbym bardzo poznać przyczynę wyłączenia przez
Waszmość pocisków broni palnej, tj., jak sądzę, wyrzucanych siłą
prochu; przypuszczam, że pociski tej broni podlegają innym zmianom i
zahamowaniom, przy oporze powietrza, niż pociski proc, łuków i kuli
ręcznych.
SALVIATI: Skłania mnie do tego nadzwyczajna, nawet nadnaturalna
gwałtowność tej broni, tak, że bez przesady mogę powiedzieć, że
prędkość, z jaką kula wychodzi z muszkietu lub z armaty, nazwać można
nadprzyrodzoną. Bo jeżeli kula taka spada naturalnie choćby z
najznaczniejszej wysokości, to prędkość jej wskutek oporu powietrza nie
będzie się stale powiększać; lecz następuje to, co się zdarza przy
spadaniu lekkich ciał już przy umiarkowanej wysokości, mianowicie, że
ruch staje się jednostajny, a dla kuli żelaznej lub ołowianej po spadku
z kilku tysięcy łokci; taką zaś najwyższą prędkość końcową osiągnąć może
w sposób naturalny ciężar spadający w powietrzu; a prędkość tę poczytuję
za mniejszą od tej, jaką tej samej kuli udziela proch. Można to wykazać
przez stosowne doświadczenie. Wystrzelmy z rusznicy, z wysokości 100
albo więcej łokci, kulę ołowianą, prostopadle na dół do bruku
kamiennego i z tej samej rusznicy wystrzelmy do tegoż bruku z
wysokości jednego lub dwóch łokci, zobaczmy następnie którym
wystrzałem bruk będzie więcej rozbity: jeżeli bowiem kula dochodząca z
wysokości słabiej działa aniżeli druga, to z pewnością powietrze ją
hamowało i zmniejszało jej prędkość, nadaną pierwotnie przez ogień;
osiągnięciu podobnej prędkości przeszkadza powietrze i kula nie nabędzie
jej nigdy, z jakkolwiek wielkiej wysokości by spadała; a jeżeli prędkość
udzielana przez ogień nie przewyższa tej, jaka może być nabyta przy
naturalnym spadku, to szybsze uderzenie na spodzie winno by być
silniejsze od mniej szybkiego. Nie wykonałem tego doświadczenia, lecz
skłonny jestem utrzymywać, że kula rusznicowa lub armatnia, spadająca z
jeszcze większej wysokości, nie zrobi takiego uderzenia jak to, które
następuje z odległości paru łokci od muru, tj. tak nieznacznej, że
krótkotrwałe rozrywanie i przecinanie powietrza nie wystarcza dla
zniesienia nadnaturalnej gwałtowności, jaką wytwarza ogień. Ten
nadmierny impet silnego wystrzału, może powodować pewne odkształcenia
krążnej pocisku, czyniąc początek paraboli mniej nachylonym, a koniec
więcej zakrzywionym. Wszakże to wszystko nie może stanowić ani małego
ani żadnego zarzutu co do poszukiwań praktycznych naszego autora, spośród których najważniejsze jest ułożenie tablicy strzałów tak zwanych
dalekonośnych (di volata), zawierającej odległości spadania kul
wystrzelonych przy różnych podniesieniach. A ponieważ te strzały
wykonywano z moździerzy, przy niewielkich nabojach; nie było więc w nich
nadnaturalnego impetu, tak, że krążne pocisków odznaczały się dokładnie.
Ale tymczasem, wróćmy do traktatu, a autor zechce nas doprowadzić do
rozpatrywania i badania impetu pocisku, poruszającego się ruchem
złożonym z dwóch jednostajnych, jednego poziomego a drugiego
skierowanego pionowo.
Twierdzenie II. Podanie II
Jeżeli jakie ciało porusza się jednostajnie w dwóch kierunkach, i to w
jednym poziomym a drugim pionowym, to ruch z tych dwóch złożony będzie
potencjalnie równy (erit potentia aequalis) momentom obu ruchów.
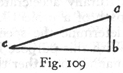 Ciało porusza się jednostajnie w dwóch kierunkach, pionowemu
odpowiada (rys. 109) droga AB; poziomemu zaś w tym samym czasie
droga BC. Ponieważ drogi AB, BC, przebywane są w tym samym czasie
ruchem jednostajnym, to momenty tych ruchów mają się do siebie jako też
same AB, BC. Ciało zaś, poruszające się według tych dwóch zmian, opisze
przekątną AC, a moment jego prędkości będzie AC. Ale AC jest
potencjalnie równe tym samym AB, BC, więc moment
złożony z dwóch momentów AB, BC jest potencjalnie równy obu razem
wziętym, c.b.d.d.
Ciało porusza się jednostajnie w dwóch kierunkach, pionowemu
odpowiada (rys. 109) droga AB; poziomemu zaś w tym samym czasie
droga BC. Ponieważ drogi AB, BC, przebywane są w tym samym czasie
ruchem jednostajnym, to momenty tych ruchów mają się do siebie jako też
same AB, BC. Ciało zaś, poruszające się według tych dwóch zmian, opisze
przekątną AC, a moment jego prędkości będzie AC. Ale AC jest
potencjalnie równe tym samym AB, BC, więc moment
złożony z dwóch momentów AB, BC jest potencjalnie równy obu razem
wziętym, c.b.d.d.
SIMPLICIO: Należałoby rozjaśnić pewną wątpliwość, która mi się
nasuwa, zdaje mi się, że co dopiero wyrażony wniosek nie zgadza się z
takimże z innego podania poprzedniego traktatu, według którego impet
ciała, biegnącego od A do B, był równy takiemuż biegnącego od A do C; tu
zaś wypada, że impet w C jest większy niż w B.
SALVIATI: Oba podania, panie Simplicio, są prawdziwe, lecz
od siebie nader różne. Tu chodzi o jedno i to samo ciało, które jeden tylko ruch
może wykonywać, ale ten ruch jest złożony z dwóch, obu jednostajnych; a
tam była mowa o dwóch ciałach spadających z jednakowym przyspieszeniem,
jedno wzdłuż prostopadłej AB, drugie po pochyłej AC. W tym ostatnim
przypadku czasy przyjmowano nierówne, bo czas spadku po pochyłej AC jest
większy niż czas spadku wzdłuż prostopadłej AB; teraz zaś rozważamy
ruchy po AB, BC, AC, jednostajne i dokonywane w tym samym czasie.
SIMPLICIO: Przepraszam, idźmy dalej, bo jestem zaspokojony.
SALVIATI: W dalszym ciągu poszukuje autor impetu ciała, ożywionego
dwoma ruchami, jednym jednostajnym poziomym, a drugim jednostajnie
przyspieszonym pionowym, z których w rezultacie składa się ruch pocisku,
opisującego linią paraboliczną; w każdym jej punkcie stara się oznaczyć,
jaki jest impet pocisku: dla zrozumienia tego podaje autor sposób albo,
powiedzmy, metodę regulowania i mierzenia tego impetu na tej linii,
wzdłuż której się odbywa spadek ciężaru ruchem naturalnie
przyspieszonym po wyjściu ze spoczynku: mówiąc:
Twierdzenie III. Podanie III
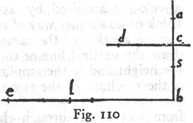 Niech będzie (rys. 110) ruch po linii AB, ze spoczynku w A i
przyjmijmy na niej jakikolwiek punkt A; i połóżmy, że samo AC
przedstawia czas albo miarę czasu spadku po AC, a także miarę impetu
albo momentu nabytego w C po spadku wzdłuż AC. Weźmy dalej na tej samej
prostej AB inny punkt B, w którym impet nabyty przez ciało przy spadku
po AB oznaczony być może w stosunku do impetu nabytego w C, którego
miarą jest AC. Połóżmy AS, średnią proporcjonalną między BA i AC.
Dowiedziemy, że impet w B ma się do impetu w C, jak linia SA do AC.
Poprowadźmy poziome, CD dwa razy większą od AC i BE dwa razy większą
od BA. Wiadomo z poprzedniego, że jeżeli ciało spada po AC, a następnie
zwrócone zostanie na poziomą CD, z impetem osiągniętym w C, to
przebiegnie tam ruchem jednostajnym drogę CD w tym samym czasie, w jakim
spadało po AC; tak samo BE przebyte zostanie w tym samym czasie co AB.
Ale czas spadku po AB jest równy AS, wiec BE przebyte będzie w czasie
AS. Połóżmy teraz, że tak się ma czas SA do czasu AC, jak EB do BL. Że
zaś ruch po EB jest jednostajny, to droga BL przebyta będzie w czasie AC
z momentem prędkości w B. Ale w tym samym czasie przebyta będzie droga
CD z momentem prędkości w C: momenty zaś prędkości mają się do siebie
jak drogi z tymi momentami przebyte w tym samym czasie: zatem moment
prędkości w C ma się do momentu prędkości w B, jak DC do BL. Że zaś jak
DC do BE, tak się mają do siebie ich połowy, tj. CA do AB, a EB do BL
ma się jak BA do AS, więc CD do BL ma się jak BA do AS, więc CD do BL ma
się jak CA do AS, tj. jak moment prędkości w C do momentu prędkości w
B, tak się ma CA do AS, albo czas spadku po CA do czasu spadku po AB.
Tak się uwydatnia metoda mierzenia impetu albo momentu prędkości na
linii prostopadłego spadku, przy czym przyjęto, że impet rośnie
proporcjonalnie do czasu.
Niech będzie (rys. 110) ruch po linii AB, ze spoczynku w A i
przyjmijmy na niej jakikolwiek punkt A; i połóżmy, że samo AC
przedstawia czas albo miarę czasu spadku po AC, a także miarę impetu
albo momentu nabytego w C po spadku wzdłuż AC. Weźmy dalej na tej samej
prostej AB inny punkt B, w którym impet nabyty przez ciało przy spadku
po AB oznaczony być może w stosunku do impetu nabytego w C, którego
miarą jest AC. Połóżmy AS, średnią proporcjonalną między BA i AC.
Dowiedziemy, że impet w B ma się do impetu w C, jak linia SA do AC.
Poprowadźmy poziome, CD dwa razy większą od AC i BE dwa razy większą
od BA. Wiadomo z poprzedniego, że jeżeli ciało spada po AC, a następnie
zwrócone zostanie na poziomą CD, z impetem osiągniętym w C, to
przebiegnie tam ruchem jednostajnym drogę CD w tym samym czasie, w jakim
spadało po AC; tak samo BE przebyte zostanie w tym samym czasie co AB.
Ale czas spadku po AB jest równy AS, wiec BE przebyte będzie w czasie
AS. Połóżmy teraz, że tak się ma czas SA do czasu AC, jak EB do BL. Że
zaś ruch po EB jest jednostajny, to droga BL przebyta będzie w czasie AC
z momentem prędkości w B. Ale w tym samym czasie przebyta będzie droga
CD z momentem prędkości w C: momenty zaś prędkości mają się do siebie
jak drogi z tymi momentami przebyte w tym samym czasie: zatem moment
prędkości w C ma się do momentu prędkości w B, jak DC do BL. Że zaś jak
DC do BE, tak się mają do siebie ich połowy, tj. CA do AB, a EB do BL
ma się jak BA do AS, więc CD do BL ma się jak BA do AS, więc CD do BL ma
się jak CA do AS, tj. jak moment prędkości w C do momentu prędkości w
B, tak się ma CA do AS, albo czas spadku po CA do czasu spadku po AB.
Tak się uwydatnia metoda mierzenia impetu albo momentu prędkości na
linii prostopadłego spadku, przy czym przyjęto, że impet rośnie
proporcjonalnie do czasu.
 Zanim pójdziemy dalej, należy nadmienić, że ponieważ ma być mowa o
ruchu złożonym z jednostajnego poziomego i przyspieszonego z góry na
dół (bo z takiego połączenia powstaje i formuje się krążna pocisku, tj. parabola), musimy przeto ustalić pewną ogólną miarę, którą by obu
ruchów prędkości, impety lub momenty (velocitatem, impetum seu momentum) mogły być mierzone. Ze zaś
niezliczone są stopnie prędkości ruchu jednostajnego, z których nie
którykolwiek przypadkowy, lecz jeden z tych niezliczonych ma być złożony
i połączony ze stopniem prędkości, nabytym w ruchu naturalnie
przyspieszonym, to nie można obmyśleć prostszej drogi wiodącej do wyboru
i oznaczenia stopnia prędkości jak przyjęcie innego tegoż rodzaju. Aby
się zatem jaśniej wyrazić; niech będzie (rys. 111) prostopadła
AC do poziomej BC: AC będzie wysokością a CB amplitudą połowy paraboli
AB, którą opisuje złożenie dwóch ruchów, z których jeden jest spadkiem
ciała po AC, ruchem naturalnie przyspieszonym, po wyjściu ze spoczynku w
A, a drugi ruchem poprzecznym jednostajnym wzdłuż poziomej AD. Impet
nabyty w C przez spadek po AC, mierzy się tąż wysokością AC, bo zawsze
ten sam jest impet ciała spadającego z tej samej wysokości: na poziomej
zaś można dla ruchów jednostajnych wyznaczać niezliczone stopnie
prędkości; aby ten, który wybiorę z tej mnogości, oznaczyć i odróżnić od
innych, i jakby palcem go wskazać, przedłużę wysokość CA w górę i na
przedłużeniu, stosownie do potrzeby, ustalę taką wysokość AE, aby ciało,
wychodzące ze spoczynku w E i po tej wysokości spadające, osiągało w A
taki impet, z jakim ma się poruszać zwrócone na poziomą AD: jest to ten
stopień prędkości, z jakim w czasie spadku po EA, przebyta będzie
wzdłuż poziomej droga równa podwójnemu EA. Uwaga ta wydała się tu
konieczną.
Zanim pójdziemy dalej, należy nadmienić, że ponieważ ma być mowa o
ruchu złożonym z jednostajnego poziomego i przyspieszonego z góry na
dół (bo z takiego połączenia powstaje i formuje się krążna pocisku, tj. parabola), musimy przeto ustalić pewną ogólną miarę, którą by obu
ruchów prędkości, impety lub momenty (velocitatem, impetum seu momentum) mogły być mierzone. Ze zaś
niezliczone są stopnie prędkości ruchu jednostajnego, z których nie
którykolwiek przypadkowy, lecz jeden z tych niezliczonych ma być złożony
i połączony ze stopniem prędkości, nabytym w ruchu naturalnie
przyspieszonym, to nie można obmyśleć prostszej drogi wiodącej do wyboru
i oznaczenia stopnia prędkości jak przyjęcie innego tegoż rodzaju. Aby
się zatem jaśniej wyrazić; niech będzie (rys. 111) prostopadła
AC do poziomej BC: AC będzie wysokością a CB amplitudą połowy paraboli
AB, którą opisuje złożenie dwóch ruchów, z których jeden jest spadkiem
ciała po AC, ruchem naturalnie przyspieszonym, po wyjściu ze spoczynku w
A, a drugi ruchem poprzecznym jednostajnym wzdłuż poziomej AD. Impet
nabyty w C przez spadek po AC, mierzy się tąż wysokością AC, bo zawsze
ten sam jest impet ciała spadającego z tej samej wysokości: na poziomej
zaś można dla ruchów jednostajnych wyznaczać niezliczone stopnie
prędkości; aby ten, który wybiorę z tej mnogości, oznaczyć i odróżnić od
innych, i jakby palcem go wskazać, przedłużę wysokość CA w górę i na
przedłużeniu, stosownie do potrzeby, ustalę taką wysokość AE, aby ciało,
wychodzące ze spoczynku w E i po tej wysokości spadające, osiągało w A
taki impet, z jakim ma się poruszać zwrócone na poziomą AD: jest to ten
stopień prędkości, z jakim w czasie spadku po EA, przebyta będzie
wzdłuż poziomej droga równa podwójnemu EA. Uwaga ta wydała się tu
konieczną.
Zauważymy nadto, że pozioma CB zwana jest amplitudą połowy paraboli
AB. Wysokość, tj. AC, tejże paraboli osią. Linią zaś EA, przez spadek po której oznacza się impet poziomy
nazywam wyniosłością (sublimitas). Po tych uwagach i określeniach, zwracam się do dowodzeń.
SAGREDO: Zatrzymajcie się, proszę, sądzę bowiem, że tu będzie na
miejscu podnieść ten pomysł autora, wykazując jego zgodność z koncepcją
Platona oznaczania różnych prędkości biegów jednostajnych przy zmianach
obrotów ciał niebieskich; wpadł on przypadkowo na myśl, że żadne ciało nie
może przejść od spoczynku do pewnego oznaczonego stopnia prędkości,
który ma następnie stale zachowywać, nie przeszedłszy przez wszystkie
inne stopnie prędkości mniejszej, tj. właściwie mówiąc większego
opóźnienia, jakie się mieszczą między stopniem oznaczonym a stopniem
największego opóźnienia, to jest spoczynkiem; mówił on, że Bóg, po
stworzeniu ruchomych ciał niebieskich, dla nadania im tych prędkości, z
jakimi następnie miały wiecznie krążyć jednostajnie po drogach
kołowych, sprawił, że wychodząc ze spoczynku poruszały się po
wyznaczonych drogach prostolinijnych takim ruchem naturalnym, jak się
poruszają nasze ciała, wyszedłszy ze spoczynku i wciąż przyspieszają
swój bieg. I dodaje, że skoro osiągnięty został przez nie odpowiedni
stopień prędkości, który potem miał się wiecznie utrzymywać, wtedy
ruch
prostolinijny zmieniał się na kołowy, który jedyny nadaje się do
pozostawania jednostajnym, bo obiegi odbywają się bez oddalania się lub
zbliżania do pewnego celu, do którego by te ciała dążyły. Pomysł ten
godny jest Platona i tym więcej winien być ceniony, że przemilczone jego
podstawy, a odkryte przez naszego autora, po usunięciu osłonek i pozorów
poetycznych, przedstawiają go w prawdziwej postaci. I wydaje mi się
prawdopodobne, że skoro mamy z nauki astronomii dość dokładne dane o
wielkości orbit planet, ich odległości od środka, wokół którego krążą,
jak ich prędkości, to i nasz autor (dla którego pomysł Platona nie jest
tajemnicą) zapewne nieraz z ciekawości myślał o rozpoczęciu badań nad
znalezieniem pewnej określonej wyniosłości (sublimita), wzdłuż jakiej
wychodzące ze stanu spoczynku planety musiałyby się poruszać, po
oznaczonych drogach prostolinijnych, biegem naturalnie przyspieszonym,
aby następnie prędkość nabyta odpowiadała przy ruchu jednostajnym
wielkościom ich orbit i czasom ich obrotów.
SALVIATI: Przypominam sobie, że mi opowiadał o zrobieniu takiego
obliczenia i znalezienia przy tym zgodności z obserwacjami; ale nie
chciał więcej o tym mówić, obawiając się, aby liczne nowości, jakie
odkrył i które wywołały oburzenie wśród wielu, nie roznieciły nowych
iskier. Kto by jednak miał ochotę, może na podstawie wskazówek,
zawartych w traktacie jaki mamy przed sobą, uczynić zadość swemu
upodobaniu. Ale wróćmy do naszego przedmiotu.
Zadanie I. Podanie IV
Jakim sposobem, w poszczególnych punktach danej paraboli, opisanej
przez pocisk, określa się impet.
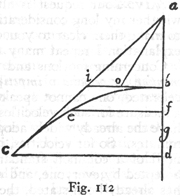 Niech będzie (rys. 112) połowa paraboli BEC, jej amplituda
CD, wysokość DB, która w górę przedłużona spotyka w A styczną CA do
paraboli, a przez wierzchołek B poprowadzona równoległa BI do poziomu
CD. Jeżeli amplituda CD jest równa całej wysokości DA, to będzie BI
równe BA i równe BD. A jeżeli przyjmiemy, że AB jest miarą czasu spadku
po AB i miarą momentu prędkości nabytego w B przy spadku wzdłuż AB po
wyjściu ze spoczynku w A, to DC
(podwojone BI) będzie drogą, która z impetem
osiągniętym wzdłuż AB, po skierowaniu ciała na poziomą przebyta
zostanie w tym samym czasie. Lecz w ciągu tegoż czasu, ciało spadające
po BD ze spoczynku w B, przebywa wysokość BD, więc spadające po AB ze
spoczynku w A, zwrócone z impetem AB na poziomą, przebiegnie drogę
równą DC. Przyłączający się spadek po BD przebywa wysokość BD; i
opisana zostaje parabola BC: na której impet w końcu C składa się z
jednostajnego poprzecznego; którego moment jest AB i z drugiego momentu
nabytego przy spadku BD w końcu D czyli C; które to oba momenty są
sobie równe. Jeżeli więc AB jest miarą jednego z nich, mianowicie
jednostajnego poprzecznego, to BI równe BD będzie miarą impetu
osiągniętego w D lub C, a prosta IA będzie ilością momentu złożonego z
obu: będzie więc ona także ilością czyli miarą całego momentu, jaki
pocisk biegnący po paraboli BC posiada jako impet w C. To założywszy,
weźmy na paraboli jakikolwiek punkt E, w którym oznaczony ma być impet
pocisku. Poprowadźmy poziomą EF i weźmy BG średnią proporcjonalną
między BD i BF. Ponieważ AB, czyli BD, jest miarą czasu i momentu
prędkości (momentum velocitatis) przy spadku BD ze spoczynku w B, to BG będzie czasem, albo
miarą czasu impetu w F przy zejściu z B. Jeżeli zatem położymy BO równe
BG, to łącząca przekątna AO będzie ilością impetu w punkcie E; albowiem
AB przyjęto jako miarę czasu i impetu w B, który po skierowaniu ciała na
poziomą dalej się utrzymuje; BO zaś określa impet w F, albo w E, przy
spadku ze spoczynku w B wzdłuż wysokości BF, te zaś AB, BO, równoważone
są potencjalnie przez AO, otrzymuje się więc co było żądane.
Niech będzie (rys. 112) połowa paraboli BEC, jej amplituda
CD, wysokość DB, która w górę przedłużona spotyka w A styczną CA do
paraboli, a przez wierzchołek B poprowadzona równoległa BI do poziomu
CD. Jeżeli amplituda CD jest równa całej wysokości DA, to będzie BI
równe BA i równe BD. A jeżeli przyjmiemy, że AB jest miarą czasu spadku
po AB i miarą momentu prędkości nabytego w B przy spadku wzdłuż AB po
wyjściu ze spoczynku w A, to DC
(podwojone BI) będzie drogą, która z impetem
osiągniętym wzdłuż AB, po skierowaniu ciała na poziomą przebyta
zostanie w tym samym czasie. Lecz w ciągu tegoż czasu, ciało spadające
po BD ze spoczynku w B, przebywa wysokość BD, więc spadające po AB ze
spoczynku w A, zwrócone z impetem AB na poziomą, przebiegnie drogę
równą DC. Przyłączający się spadek po BD przebywa wysokość BD; i
opisana zostaje parabola BC: na której impet w końcu C składa się z
jednostajnego poprzecznego; którego moment jest AB i z drugiego momentu
nabytego przy spadku BD w końcu D czyli C; które to oba momenty są
sobie równe. Jeżeli więc AB jest miarą jednego z nich, mianowicie
jednostajnego poprzecznego, to BI równe BD będzie miarą impetu
osiągniętego w D lub C, a prosta IA będzie ilością momentu złożonego z
obu: będzie więc ona także ilością czyli miarą całego momentu, jaki
pocisk biegnący po paraboli BC posiada jako impet w C. To założywszy,
weźmy na paraboli jakikolwiek punkt E, w którym oznaczony ma być impet
pocisku. Poprowadźmy poziomą EF i weźmy BG średnią proporcjonalną
między BD i BF. Ponieważ AB, czyli BD, jest miarą czasu i momentu
prędkości (momentum velocitatis) przy spadku BD ze spoczynku w B, to BG będzie czasem, albo
miarą czasu impetu w F przy zejściu z B. Jeżeli zatem położymy BO równe
BG, to łącząca przekątna AO będzie ilością impetu w punkcie E; albowiem
AB przyjęto jako miarę czasu i impetu w B, który po skierowaniu ciała na
poziomą dalej się utrzymuje; BO zaś określa impet w F, albo w E, przy
spadku ze spoczynku w B wzdłuż wysokości BF, te zaś AB, BO, równoważone
są potencjalnie przez AO, otrzymuje się więc co było żądane.
SAGREDO: Rozważanie, tak składania tych różnych impetów, jak i ilości
impetu wypadkowego, wydaje mi się tak nowem, że doznaję niemałej
konfuzji. Nie mówię o składaniu dwóch ruchów jednostajnych, jakkolwiek
niejednakowych, gdyż jeden jest poziomy a drugi pionowy, bo te są
najodpowiedniejsze do wytworzenia ruchu potencjalnie równego obu
składowym, lecz nie mogę zdać sobie sprawy z połączenia ruchu
jednostajnego poziomego z przyspieszonym prostopadłym. Dlatego
prosiłbym o nieco gruntowniejszy wykład tego przedmiotu.
SIMPLICIO: I dla mnie jest to potrzebne, tym więcej, że nie jestem
jeszcze całkowicie przekonany o potrzebie tych twierdzeń, stanowiących
jakby podstawę innych, które po nich następują. Przyznam się, że nawet
przy składaniu dwóch ruchów jednostajnych, poziomego i pionowego,
pragnąłbym lepiej zdawać sobie sprawę z potęgi wypadkowej. Teraz, panie
Salviati, zechce Waszmość uczynić zadość naszej potrzebie i życzeniu.
SALVIATI: Życzenia Wasze są zupełnie uzasadnione, a ponieważ dłuższy
czas nad tym myślałem, spróbuję uczynić im zadość. Pozwólcie tymczasem,
że wrócę do rzeczy, wielokrotnie już poruszanych
przez autora.
Rozprawiać stanowczo o ruchach, ich prędkości lub impecie, czy to
jednostajnych, czy też naturalnie przyspieszonych, nie możemy, nie
określiwszy najpierw miary, której by użyć można do mierzenia
prędkości, a także do mierzenia czasu. Co do miary czasu, to mamy
ogólnie przyjęte godziny, minuty pierwsze i drugie itd., a
tak samo jak dla czasu, musimy mieć i dla prędkości miarę dla
wszystkich zrozumiałą i ogólnie przyjętą, czyli wszędzie jednakową.
Za odpowiednią do tego użytku uważał autor, jak tu powiedziano,
prędkość ciała swobodnie spadającego, bo wszędzie na ziemi prędkości
jednakowo rosną. Gdyż stopień prędkości, jaki np. osiąga po wyjściu ze
spoczynku jednofuntowa kula ołowiana, spadająca prostopadle z wysokości,
jednego pręta (una pieca) jest zawsze ten sam we wszystkich
miejscowościach, a przez to najodpowiedniejszy do wyrażenia ilości
impetu, pochodzącego z naturalnego spadku. Pozostaje więc jeszcze szukać
metody oznaczania ilości impetu w ruchu jednostajnym w taki sposób, aby
wszyscy ci, którzy o niej będą mówić, wytwarzali sobie to samo pojęcie
o jego wielkości i prędkości; aby jeden nie wyobrażał sobie impetu
prędszego niż drugi; a następnie, aby przy łączeniu i mieszaniu
powstałych z ruchu jednostajnego i przyspieszonego, różni ludzie nie
tworzyli sobie różnych pojęć o różnych wielkościach impetów. Dla
oznaczania i przedstawiania takiego szczególnego impetu i prędkości,
nie znalazł nasz autor innego odpowiedniejszego środka, jak posługiwać
się tym impetem, który osiąga ciało w ruchu naturalnie przyspieszonym,
którego każdy moment osiągnięty, przy zmianie ruchu na jednostajny,
zatrzymuje swoją prędkość ściśle określoną i taką, że w ciągu czasu
równego czasowi spadku przebyta będzie długość, równa podwójnej
wysokości spadku. Lecz ponieważ jest to główny punkt rozważanej
kwestii, dobrze będzie objaśnić go szczególnym przykładem. Wracając więc
do prędkości i impetu nabytego przez ciało spadające, jak
powiedzieliśmy, z wysokości jednego pręta, którą to prędkością chcemy
się posługiwać przy mierzeniu innych prędkości lub opóźnień w innych
przypadkach i przyjmując np., że czas takiego spadku wynosić będzie
cztery sekundy, to nie powinniśmy, dla określenia impetu ciała
spadającego z jakiejkolwiek innej wysokości, większej lub mniejszej,
brać stosunku tej ostatniej wysokości do jednego pręta; przyjmując np.,
że przy czterokrotnie większej wysokości spadku, osiągnięta zostanie
prędkość cztery razy większa; to bowiem byłoby mylne; gdyż przy ruchu
naturalnie przyspieszonym, prędkość ani
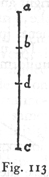 rośnie ani się zmniejsza
proporcjonalnie do drogi, a tylko proporcjonalnie do czasu, drogi zaś
rosną proporcjonalnie do kwadratów z czasu, jak to było dowiedzione. Bo
gdybyśmy mieli na linii prostej oznaczoną pewną jej część, jako miarę
prędkości, a także jako miarę czasu i przebytej w ciągu tego czasu
drogi (które trzy wielkości, dla skrócenia przedstawiane są często przez
jedną i też samą linię), to dla zmierzenia czasu i stopnia prędkości,
który by to samo ciało osiągnęło na innej odległości, brać musimy jako
miarę nie bezpośrednio tę ostatnią odległość, lecz średnią
proporcjonalną między dwiema odległościami. Lecz lepiej to objaśnię na
przykładzie. Wyobraźmy sobie (rys. 113), że wzdłuż linii AC,
prostopadłej do poziomu, przebywa ciało jej część AB ruchem
przyspieszonym naturalnego spadku: czas trwania tego spadku przedstawić
mogę jakąkolwiek linią, a w skrócie przedstawię go przez tę samą
linią AB, którą przyjmę także za miarę impetu i nabytej w tym ruchu
prędkości, tak że dla wszystkich wielkości, branych pod uwagę w ciągu
rozmowy, miarą będzie AB. Ustaliwszy naszem dowolnym przypuszczeniem, że
jedna wielkość AB przedstawia trzy miary różnego rodzaju, mianowicie
miary dróg, czasów i impetów, zajmiemy się oznaczeniem dla danej drogi
AC, czasu spadku od A do C i impetu osiągniętego w C, w stosunku do
czasu i impetu, których miarą jest AB. Jeden i drugi znajdziemy, biorąc
dla dwóch linii AC, AB, średnią proporcjonalną AD i ustalając, że czas
spadku po AC ma się do czasu spadku po AB jak linia AD do AB. Powiemy
tak samo, że impet, albo stopień prędkości (impeto o grado di velocità), osiągnięty w C, ma się do
impetu w B jak ta sama linia AD do AB, bo prędkość rośnie w tym samym
stosunku co i czas: a jakkolwiek ten wniosek przyjęty został jako
postulat, wszakże autor objaśniał jego zastosowanie w podaniu trzeciem.
rośnie ani się zmniejsza
proporcjonalnie do drogi, a tylko proporcjonalnie do czasu, drogi zaś
rosną proporcjonalnie do kwadratów z czasu, jak to było dowiedzione. Bo
gdybyśmy mieli na linii prostej oznaczoną pewną jej część, jako miarę
prędkości, a także jako miarę czasu i przebytej w ciągu tego czasu
drogi (które trzy wielkości, dla skrócenia przedstawiane są często przez
jedną i też samą linię), to dla zmierzenia czasu i stopnia prędkości,
który by to samo ciało osiągnęło na innej odległości, brać musimy jako
miarę nie bezpośrednio tę ostatnią odległość, lecz średnią
proporcjonalną między dwiema odległościami. Lecz lepiej to objaśnię na
przykładzie. Wyobraźmy sobie (rys. 113), że wzdłuż linii AC,
prostopadłej do poziomu, przebywa ciało jej część AB ruchem
przyspieszonym naturalnego spadku: czas trwania tego spadku przedstawić
mogę jakąkolwiek linią, a w skrócie przedstawię go przez tę samą
linią AB, którą przyjmę także za miarę impetu i nabytej w tym ruchu
prędkości, tak że dla wszystkich wielkości, branych pod uwagę w ciągu
rozmowy, miarą będzie AB. Ustaliwszy naszem dowolnym przypuszczeniem, że
jedna wielkość AB przedstawia trzy miary różnego rodzaju, mianowicie
miary dróg, czasów i impetów, zajmiemy się oznaczeniem dla danej drogi
AC, czasu spadku od A do C i impetu osiągniętego w C, w stosunku do
czasu i impetu, których miarą jest AB. Jeden i drugi znajdziemy, biorąc
dla dwóch linii AC, AB, średnią proporcjonalną AD i ustalając, że czas
spadku po AC ma się do czasu spadku po AB jak linia AD do AB. Powiemy
tak samo, że impet, albo stopień prędkości (impeto o grado di velocità), osiągnięty w C, ma się do
impetu w B jak ta sama linia AD do AB, bo prędkość rośnie w tym samym
stosunku co i czas: a jakkolwiek ten wniosek przyjęty został jako
postulat, wszakże autor objaśniał jego zastosowanie w podaniu trzeciem.
Po dobrym zrozumieniu i ustaleniu powyższego, weźmiemy pod uwagę
impet pochodzący z dwóch ruchów złożonych; jednego złożonego z
poziomego i zawsze jednostajnego, oraz prostopadłego do poziomu, także
jednostajnego. Ale drugi złożony będzie z poziomego jednostajnego i
prostopadłego naturalnie przyspieszonego. Gdy oba są jednostajne, to jak
widzieliśmy co dopiero, impet wypadkowy ze złożenia obu jest obu równy
potencjalnie, co dla jasności objaśnimy na przykładzie. Wyobraźmy
sobie, że ciało, spadające po
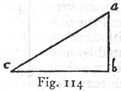 prostopadłej AB (rys. 114) ma np.
3 stopnie impetu równomiernego, ale przenoszone jest przez AB ku C z
prędkością i impetem 4 stopni, tak, że w tym samym czasie, gdy
spadając przebiegnie po prostopadłej 3 łokcie, to po poziomej
przejdzie 4; lecz przez złożenie obu prędkości przejdzie ono w ciągu
tego czasu od A do C, postępując ciągle po przekątnej AC, której długość
nie wynosi 7, to jest sumy z AB, 3 i BC, 4, ale 5, które potencjalnie
jest równe obu 3 i 4. Bo jeżeli weźmiemy kwadraty z 3 i 4, to jest 9 i
18 i połączymy je, to utworzą razem 25, jako kwadrat z AC, równy obu
kwadratom z AB i BC, a więc AC będzie bokiem, a raczej pierwiastkiem
kwadratu 25, czyli będzie 5. Przyjąć więc należy, za prawidło ścisłe i
pewne, że gdy chodzi o oznaczenie ilości impetu, złożonego z dwóch
impetów danych, jednego poziomego, drugiego prostopadłego a obu
jednostajnych, należy utworzyć z nich kwadraty i dodać do siebie,
następnie wyciągnąć pierwiastek z sumy, który da ilość impetu złożonego
z obu. I jak w naszym przykładzie ciało wskutek ruchu prostopadłego
miałoby popchnięcie do poziomu z siłą 3 stopni, a w ruchu poziomym
uderzenie w C z 4 stopniami, popychane przez oba połączone impety,
będzie ono jakby uderzone i poruszające się z 5 stopniami prędkości i
siły. A uderzenie to mieć będzie tę samą wartość we wszystkich
punktach przekątnej AC, dopókąd impety składowe pozostają te same, nie
rosną i nie zmniejszają się.
prostopadłej AB (rys. 114) ma np.
3 stopnie impetu równomiernego, ale przenoszone jest przez AB ku C z
prędkością i impetem 4 stopni, tak, że w tym samym czasie, gdy
spadając przebiegnie po prostopadłej 3 łokcie, to po poziomej
przejdzie 4; lecz przez złożenie obu prędkości przejdzie ono w ciągu
tego czasu od A do C, postępując ciągle po przekątnej AC, której długość
nie wynosi 7, to jest sumy z AB, 3 i BC, 4, ale 5, które potencjalnie
jest równe obu 3 i 4. Bo jeżeli weźmiemy kwadraty z 3 i 4, to jest 9 i
18 i połączymy je, to utworzą razem 25, jako kwadrat z AC, równy obu
kwadratom z AB i BC, a więc AC będzie bokiem, a raczej pierwiastkiem
kwadratu 25, czyli będzie 5. Przyjąć więc należy, za prawidło ścisłe i
pewne, że gdy chodzi o oznaczenie ilości impetu, złożonego z dwóch
impetów danych, jednego poziomego, drugiego prostopadłego a obu
jednostajnych, należy utworzyć z nich kwadraty i dodać do siebie,
następnie wyciągnąć pierwiastek z sumy, który da ilość impetu złożonego
z obu. I jak w naszym przykładzie ciało wskutek ruchu prostopadłego
miałoby popchnięcie do poziomu z siłą 3 stopni, a w ruchu poziomym
uderzenie w C z 4 stopniami, popychane przez oba połączone impety,
będzie ono jakby uderzone i poruszające się z 5 stopniami prędkości i
siły. A uderzenie to mieć będzie tę samą wartość we wszystkich
punktach przekątnej AC, dopókąd impety składowe pozostają te same, nie
rosną i nie zmniejszają się.
Zobaczmy teraz, co następuje przy składaniu ruchu jednostajnego
poziomego z ruchem prostopadłym do poziomu, który zaczynając od
spoczynku postępuje z naturalnym przyspieszeniem. Oczywiście przekątna,
będąca linią ruchu z tych dwóch złożonego, nie jest linią prostą lecz
półparabolą, jak to było dowiedzione; wzdłuż której impet wciąż
wzrasta, dzięki ciągłemu wzrostowi prędkości ruchu prostopadłego. Toteż dla określenia, jaki będzie impet w danym punkcie tej przekątnej
parabolicznej, trzeba najpierw oznaczyć ilość impetu jednostajnego
poziomego, a następnie badać, jaki będzie impet spadku w danym punkcie;
to rozważanie czasu nie było potrzebne przy składaniu dwóch ruchów
jednostajnych, bo ich prędkości i impety były wciąż te same; tu
przeciwnie, gdy przychodzi składać ruch, który począwszy od
największego opóźnienia, postępuje z prędkością rosnącą razem z czasem,
konieczne jest, aby ilość czasu wykazywała ilość stopnia prędkości w
danym punkcie: w rezultacie więc impet złożony z tych dwóch (jak dla
naszych ruchów jednostajnych) będzie
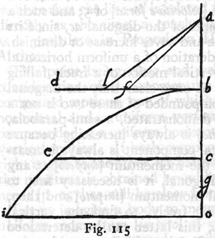 potencjalnie równy obu składowym. Ale lepiej jeszcze objaśnię to na przykładzie.
Niech będzie (rys. 115) na prostopadłej do poziomu AC wzięta jakakolwiek część AB,
która jednocześnie mierzy drogę ruchu naturalnego po tej prostopadłej,
a także jest miarą czasu i stopnia prędkości a raczej impetu.
Oczywistem jest najpierw, że impet ciała spadającego z A przemieni się w
B na ruch jednostajnie wzdłuż BD równoległej do poziomu, a ilość
prędkości tego ruchu będzie taka, że w ciągu czasu AB ciało przebiegnie
podwójną drogę AB i tak długą niech będzie BD. Połóżmy dalej BC=BA,
poprowadźmy CE równoległą do BD i jej równą, i opiszmy przez punkty B,
E, linią paraboliczną BEI. A ponieważ w ciągu czasu AB z impetem AB
przebywana jest pozioma BD lub CE, dwa razy większa od AB i w tym
samym czasie prostopadła BC z impetem nabytym w C, równym poziomemu,
więc ciało po upływie czasu AB znajdzie się w B, przebywszy od E
parabolę BE, i mieć będzie impet złożony z dwóch, z których każdy jest
równy impetowi AB. A ponieważ jeden z nich jest poziomy, a drugi
pionowy, to impet wypadkowy będzie potencjalnie równy obu składowym.
Połóżmy więc BF=BA i poprowadźmy przekątną AF; impet i uderzenie w E
będzie większe od uderzenia w B, ciała spadającego z wysokości A, albo
od uderzenia impetu poziomego wzdłuż BD, w stosunku AF do AB. Ale jeżeli
uważamy zawsze BA za miarę drogi spadku od spoczynku w A do B, oraz
miarę czasu i impetu, jaki ciało spadające nabywa w B, to wysokość BO
nie byłaby równą ale większą od AB; wziąwszy BG średnią proporcjonalną
między AB i BO, będzie BG miarą czasu i impetu w O, nabytego przy spadku
z wysokości BO; droga po poziomej, która przebyła z impetem AB w ciągu
czasu AB była dwa razy większa od AB, będzie w ciągu czasu BG o tyle
większa, o ile BG jest większe od BA. Połóżmy LB=BG i poprowadźmy
przekątną AL, a otrzymamy ilość złożoną z dwóch impetów, poziomego i
pionowego, które opisują parabolę: z nich poziomy jest jednostajny,
nabyty w B przez spadek po AB, a drugi jest nabyty w O, a raczej w I,
przez spadek po BO w ciągu czasu BG, które jest zarazem ilością jego
momentu. Podobnie znajdziemy impet w końcowym punkcie paraboli, gdy jej
wysokość będzie mniejsza od wyniosłości AB, biorąc między obiema
średnią proporcjonalną; ta, umieszczona na poziomej zamiast BF, pozwala
poprowadzić przekątną jak AF będącą ilością impetu w punkcie końcowym
paraboli.
potencjalnie równy obu składowym. Ale lepiej jeszcze objaśnię to na przykładzie.
Niech będzie (rys. 115) na prostopadłej do poziomu AC wzięta jakakolwiek część AB,
która jednocześnie mierzy drogę ruchu naturalnego po tej prostopadłej,
a także jest miarą czasu i stopnia prędkości a raczej impetu.
Oczywistem jest najpierw, że impet ciała spadającego z A przemieni się w
B na ruch jednostajnie wzdłuż BD równoległej do poziomu, a ilość
prędkości tego ruchu będzie taka, że w ciągu czasu AB ciało przebiegnie
podwójną drogę AB i tak długą niech będzie BD. Połóżmy dalej BC=BA,
poprowadźmy CE równoległą do BD i jej równą, i opiszmy przez punkty B,
E, linią paraboliczną BEI. A ponieważ w ciągu czasu AB z impetem AB
przebywana jest pozioma BD lub CE, dwa razy większa od AB i w tym
samym czasie prostopadła BC z impetem nabytym w C, równym poziomemu,
więc ciało po upływie czasu AB znajdzie się w B, przebywszy od E
parabolę BE, i mieć będzie impet złożony z dwóch, z których każdy jest
równy impetowi AB. A ponieważ jeden z nich jest poziomy, a drugi
pionowy, to impet wypadkowy będzie potencjalnie równy obu składowym.
Połóżmy więc BF=BA i poprowadźmy przekątną AF; impet i uderzenie w E
będzie większe od uderzenia w B, ciała spadającego z wysokości A, albo
od uderzenia impetu poziomego wzdłuż BD, w stosunku AF do AB. Ale jeżeli
uważamy zawsze BA za miarę drogi spadku od spoczynku w A do B, oraz
miarę czasu i impetu, jaki ciało spadające nabywa w B, to wysokość BO
nie byłaby równą ale większą od AB; wziąwszy BG średnią proporcjonalną
między AB i BO, będzie BG miarą czasu i impetu w O, nabytego przy spadku
z wysokości BO; droga po poziomej, która przebyła z impetem AB w ciągu
czasu AB była dwa razy większa od AB, będzie w ciągu czasu BG o tyle
większa, o ile BG jest większe od BA. Połóżmy LB=BG i poprowadźmy
przekątną AL, a otrzymamy ilość złożoną z dwóch impetów, poziomego i
pionowego, które opisują parabolę: z nich poziomy jest jednostajny,
nabyty w B przez spadek po AB, a drugi jest nabyty w O, a raczej w I,
przez spadek po BO w ciągu czasu BG, które jest zarazem ilością jego
momentu. Podobnie znajdziemy impet w końcowym punkcie paraboli, gdy jej
wysokość będzie mniejsza od wyniosłości AB, biorąc między obiema
średnią proporcjonalną; ta, umieszczona na poziomej zamiast BF, pozwala
poprowadzić przekątną jak AF będącą ilością impetu w punkcie końcowym
paraboli.
Do rozważanej metody badania impetów, strzałów, a raczej uderzeń
takich pocisków, dodać należy inną nader ważną uwagę, a mianowicie, że
dla dobrego oznaczenia siły uderzenia i jego energji nie wystarcza
rozważanie samej prędkości pocisku, lecz należy jeszcze mieć na
względzie stan i warunki, w jakich się znajduje ciało uderzane, gdyż z
wielu względów ma to wielkie znaczenie dla skuteczności uderzenia. A
najpierw, nie ma takiego, kto by nie wiedział, że ciało uderzane tym
więcej podlega gwałtownej prędkości uderzającego, im bardziej się mu
opiera i ruch jego hamuje w całości lub częściowo; i jeżeli uderzone
ustępuje przed prędkością uderzającego, to takie uderzenie nie wywiera
żadnego skutku. Ten zaś, kto pędzi by przebić lancą swego przeciwnika i
wpada na uciekającego z taką samą prędkością, nie uderzy go, lecz tylko
dotknie bez uszkodzenia.
Ale jeżeli uderzenie trafia na taki przedmiot, który uderzającemu
niezupełnie ustępuje, lecz tylko częściowo, to uderzenie uszkadza,
lecz nie całym swoim impetem, a tylko przewyżką prędkości uderzającego
nad prędkością cofania się i ustępowania uderzonego: tak, że jeżeli np. ciało uderzające dochodzi do uderzonego z 10
stopniami prędkości, a to ostatnie, ustępując częściowo cofa się z 4
stopniami, to impet i uderzenie wynosić będzie 6 stopni. Uderzenie
wreszcie będzie zupełne i największe odnośnie do ciała uderzającego,
gdy ciało uderzane wcale nie ustępuje, lecz całkowicie się opiera i
wstrzymuje cały ruch uderzającego; jeżeli to może się zdarzyć.
Powiedziałem, odnośnie do ciała uderzającego, bo jeżeli by ciało
uderzone poruszało się w odwrotnym kierunku, tj. w stronę
uderzającego, to strzał i uderzenie będą tym silniejsze, im obie
przeciwne prędkości razem wzięte są większe od prędkości ciała
uderzającego. Nadto zauważyć należy, że większe lub mniejsze ustępowanie
zależy nie tylko od mniejszej lub większej twardości tworzywa, jakby to
było żelazo, ołów, wełna itp., ale także od położenia ciała
otrzymującego uderzenie; jeżeli to położenie jest takie, że ruch ciała
uderzającego spotyka je pod kątem prostym, to impet strzału będzie
największy: lecz jeżeli ruch będzie nachylony, jakbyśmy powiedzieli,
ukośny, to cios będzie słabszy i to tym więcej, im większe będzie
nachylenie, bo tak położony przedmiot, choćby był z najtwardszego
tworzywa, nie niszczy i nie zatrzymuje całego impetu i ruchu ciała
uderzającego, które wymykając się leci dalej, wykonując ruch swój
częściowo tylko na powierzchni opierającej się przeszkody. Gdy więc
poprzednio oznaczano wielkość impetu pocisku na końcu paraboli, to miano
zawsze na względzie uderzenie prostopadłe do tej paraboli albo do
stycznej do niej w danym punkcie; bo jeżeli ten ruch złożony jest z
poziomego i prostopadłego, to uderzenie nie wywiera swego maksymalnego
działania ani na płaszczyznę poziomą ani na pionową, gdyż względem obu
otrzymane zostaje ukośnie.
SAGREDO: Rozważanie tych uderzeń przypomina mi zagadnienie albo
raczej jedną kwestię z mechaniki, której rozwiązania nie znalazłem u
żadnego autora, ani nawet wzmianki, która by mnie choć w części
zadowoliła. Moje powątpiewanie i podziw polegają na tem, że nie mam
przeświadczenia, skąd może pochodzić i od czego zależy energia i
niezmierna siła, objawiająca się podczas uderzenia, gdy jednym ciosem
młotka, nie ważącego więcej jak 8 do 10 funtów, pokonujemy takie opory,
które nie ustępują żadnemu ciężarowi działającemu bez uderzenia a tylko
z impetem naciskowym, choćby ten ciężar wynosił wieleset funtów.
Pragnąłbym bardzo poznać sposób mierzenia siły tego uderzenia, która,
nie sądzę, aby była nieskończona, uważam raczej, że ma pewną wartość
oznaczoną, która mogłaby być porównana z innymi
siłami naciskającemi ciężkości i wreszcie zmierzona, albo drąga, albo śruby, albo innych
narzędzi mechanicznych, których zwiększenie siły jest dla mnie w
zupełności zrozumiałe.
SALVIATI: Nie sam pan tylko podziwia to działanie, nie mając jasnego
pojęcia o przyczynie zadziwiającego zjawiska. Rozmyślałem nad nim
pewien czas na próżno i wciąż się zwiększała moja niepewność, aż w
końcu, spotkawszy raz naszego Akademika, podwójnie zostałem przezeń
pocieszony: dowiedziałem się najpierw, że i on także pozostawał przez
długi czas w podobnej nieświadomości, następnie powiedział mi, że
poświęciwszy wiele tysięcy godzin swego życia na zastanawianie się i
badanie, doszedł do niektórych wyników, bardzo dalekich od naszych
bezpośrednich wyobrażeń, a przez to nowych i swą nowością
zadziwiających. A jakkolwiek wiem, że Waszmość pragnął, aby się
zapoznać z takimi pomysłami, nader oddalonemi od panujących poglądów, to
jednak obecnie nie będę mógł uczynić zadość żądaniu, lecz przyrzekam,
że, gdy ukończymy czytanie tego traktatu, objaśnię wszystkie tę pomysły
i nadzwyczajności, które mi pozostały w pamięci z rozmów z naszym
Akademikiem. A tymczasem podążajmy za podaniami autora.
Zadanie II. Podanie V
Na przedłużeniu osi danej paraboli oznaczyć punkt najwyższy, z
którego spadające ciało opisze daną parabolę.
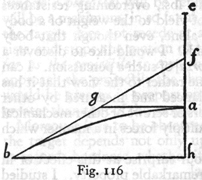 Niech będzie (rys. 116) parabola AB, jej amplituda HB,
przedłużenie jej osi HE, na którym ma być oznaczona wyniosłość, z
której spadające ciało, z impetem osiągniętym w A zwrócone na poziomą,
opisuje parabolę AB. Poprowadźmy poziomą AG, równoległą do BH i połóżmy
AF=AH, poprowadźmy prostą FB, styczną do paraboli w B, a przecinającą w
G poziomą AG; odetnijmy AE trzecią proporcjonalną
do FA i AG. Twierdzę, że E będzie szukanym punktem, z którego ciało,
wychodzące ze spoczynku w E i z nabytym impetem w A skierowane poziomo
razem z impetem spadku ze spoczynku w A do H, opisze parabolę AB. Bo
jeżeli EA jest czasem spadku od E do A a jednocześnie miarą impetu
nabytego w A, to będzie AG (średnia proporcjonalna między EA i AF)
czasem spadku i impetu przy spadku z F do A, albo z A do H. A ponieważ
ciało spadające z E, z impetem nabytym w A, przebędzie ruchem
jednostajnym na poziomie drogę równą podwojonemu EA, a w czasie i z
impetem AG drogę równą podwojonemu GA czyli BH (bo przy ruchu
jednostajnym drogi są proporcjonalne do czasów), a w ruchu prostopadłym
ze spoczynku w czasie GA przebiegnie drogę AH; zatem w tym
samym czasie przebyta będzie przez ciało amplituda HB i wysokość AH.
Ciało więc spadające z E opisze parabolę AB, jak to było założone.
Niech będzie (rys. 116) parabola AB, jej amplituda HB,
przedłużenie jej osi HE, na którym ma być oznaczona wyniosłość, z
której spadające ciało, z impetem osiągniętym w A zwrócone na poziomą,
opisuje parabolę AB. Poprowadźmy poziomą AG, równoległą do BH i połóżmy
AF=AH, poprowadźmy prostą FB, styczną do paraboli w B, a przecinającą w
G poziomą AG; odetnijmy AE trzecią proporcjonalną
do FA i AG. Twierdzę, że E będzie szukanym punktem, z którego ciało,
wychodzące ze spoczynku w E i z nabytym impetem w A skierowane poziomo
razem z impetem spadku ze spoczynku w A do H, opisze parabolę AB. Bo
jeżeli EA jest czasem spadku od E do A a jednocześnie miarą impetu
nabytego w A, to będzie AG (średnia proporcjonalna między EA i AF)
czasem spadku i impetu przy spadku z F do A, albo z A do H. A ponieważ
ciało spadające z E, z impetem nabytym w A, przebędzie ruchem
jednostajnym na poziomie drogę równą podwojonemu EA, a w czasie i z
impetem AG drogę równą podwojonemu GA czyli BH (bo przy ruchu
jednostajnym drogi są proporcjonalne do czasów), a w ruchu prostopadłym
ze spoczynku w czasie GA przebiegnie drogę AH; zatem w tym
samym czasie przebyta będzie przez ciało amplituda HB i wysokość AH.
Ciało więc spadające z E opisze parabolę AB, jak to było założone.
Wniosek
Wynika stąd, że połowa podstawy, albo połowa amplitudy półparaboli
(która jest czwartą częścią amplitudy całej paraboli), jest średnią
proporcjonalną między jej wysokością a wyniosłością, z której spadek ją
opisuje.
Zadanie III. Podanie VI
Dana jest wyniosłość i wysokość połowy paraboli, znaleźć jej
amplitudę.
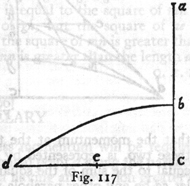 Niech będzie AC (rys. 117), prostopadła do poziomej DC, na
której dana jest wysokość CB i wyniosłość BA. Oznaczyć trzeba na
poziomej CD amplitudę tej półparaboli, którą ciało z wyniosłości BA
opisze z wysokością BC. Weźmy średnią proporcjonalną między CB i BA i
odetnijmy CD równą tejże podwojonej. Twierdzę, że CD będzie szukaną
amplitudą. Wynika to z poprzedniego.
Niech będzie AC (rys. 117), prostopadła do poziomej DC, na
której dana jest wysokość CB i wyniosłość BA. Oznaczyć trzeba na
poziomej CD amplitudę tej półparaboli, którą ciało z wyniosłości BA
opisze z wysokością BC. Weźmy średnią proporcjonalną między CB i BA i
odetnijmy CD równą tejże podwojonej. Twierdzę, że CD będzie szukaną
amplitudą. Wynika to z poprzedniego.
Twierdzenie IV. Podanie VII
Spomiędzy ciał, opisujących półparabolę jednakowej amplitudy, to,
które opisuje parabolę o amplitudzie równej podwójnej wysokości, będzie
miało mniejszy impet od każdego innego.
Niech będzie (rys. 118) półparabola BD, której amplituda CD
jest dwa razy większa od wysokości CB, odetnijmy na górnym przedłużeniu
osi BA równe wysokości BC: poprowadźmy AD styczną do paraboli w D a
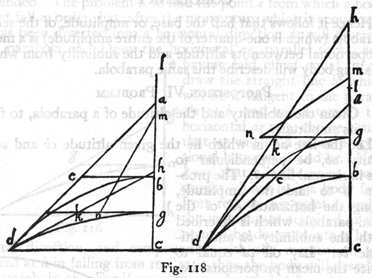 poziomą BE przecinającą w E, będzie więc BE równe BC albo równe BA;
wiadomo, że parabolę opisuje ciało, którego impet jednostajny poziomy
jest taki jak nabyty w B przy spadku ze spoczynku w A, a impet naturalny
z góry na dół, jak w C przy spadku ze spoczynku w B. Wynika stąd, że
impet z tych dwóch złożony, działający w punkcie końcowym D będzie jak
przekątna AE równy potencjalnie obu. Niech będzie GD jakakolwiek inna
półparabola z tą samą amplitudą CD, lecz z wysokością CG, mniejszą lub
większą od wysokości BC; styczną do niej będzie HD, przecinająca poziomą
przeprowadzoną przez G w punkcie K; i niech będzie jak HG do GK, tak
KG do GL, z której to wysokości GL, wedle tego co poprzednio
dowiedziono, spadające ciało opisuje parabolę GD. Między AB i GL niech
będzie średnia proporcjonalna GM: to GM będzie czasem i momentem albo
impetem w G przy spadku z L (założono bowiem, że AB jest miarą czasu i
impetu). Niech będzie znów, między HC i CG średnia proporcjonalna GN,
będzie ona miarą czasu i impetu przy spadku z G do C. Jeżeli
poprowadzimy MN, to będzie ono miarą impetu ciała opisującego parabolę
BD, osiągniętego w punkcie końcowym D. Twierdzę, że impet ten jest
większy od impetu na paraboli BD, który się równał AE. Albowiem GN jest
średnią między BC i CG, a że BC równe BE, to jest równe GK (bo obie są
połową DC); będzie więc jak CG do GN, tak NG do GK i jak CG albo HG do
GK, tak kwadrat z NG do kwadratu z GK; jak zatem HG do GK, tak się ma KG
do GL a więc jak kwadrat z NG do kwadratu z GK, tak się ma KG do GL;
lecz jak KG do GL, tak się ma kwadrat z KG do kwadratu z GM (bo GM jest
średnią między KG i GL), a więc trzy kwadraty NG, GK i GM tworzą ciąg
proporcjonalny, a dwa skrajne NG i GM razem
wzięte dają kwadrat z NM większy od podwojonego kwadratu z KG, który
jest równy podwojonemu kwadratowi z AE: więc kwadrat z MN jest większy
od kwadratu z AE i linia NM większa od linii EA, c.b.d.d.
poziomą BE przecinającą w E, będzie więc BE równe BC albo równe BA;
wiadomo, że parabolę opisuje ciało, którego impet jednostajny poziomy
jest taki jak nabyty w B przy spadku ze spoczynku w A, a impet naturalny
z góry na dół, jak w C przy spadku ze spoczynku w B. Wynika stąd, że
impet z tych dwóch złożony, działający w punkcie końcowym D będzie jak
przekątna AE równy potencjalnie obu. Niech będzie GD jakakolwiek inna
półparabola z tą samą amplitudą CD, lecz z wysokością CG, mniejszą lub
większą od wysokości BC; styczną do niej będzie HD, przecinająca poziomą
przeprowadzoną przez G w punkcie K; i niech będzie jak HG do GK, tak
KG do GL, z której to wysokości GL, wedle tego co poprzednio
dowiedziono, spadające ciało opisuje parabolę GD. Między AB i GL niech
będzie średnia proporcjonalna GM: to GM będzie czasem i momentem albo
impetem w G przy spadku z L (założono bowiem, że AB jest miarą czasu i
impetu). Niech będzie znów, między HC i CG średnia proporcjonalna GN,
będzie ona miarą czasu i impetu przy spadku z G do C. Jeżeli
poprowadzimy MN, to będzie ono miarą impetu ciała opisującego parabolę
BD, osiągniętego w punkcie końcowym D. Twierdzę, że impet ten jest
większy od impetu na paraboli BD, który się równał AE. Albowiem GN jest
średnią między BC i CG, a że BC równe BE, to jest równe GK (bo obie są
połową DC); będzie więc jak CG do GN, tak NG do GK i jak CG albo HG do
GK, tak kwadrat z NG do kwadratu z GK; jak zatem HG do GK, tak się ma KG
do GL a więc jak kwadrat z NG do kwadratu z GK, tak się ma KG do GL;
lecz jak KG do GL, tak się ma kwadrat z KG do kwadratu z GM (bo GM jest
średnią między KG i GL), a więc trzy kwadraty NG, GK i GM tworzą ciąg
proporcjonalny, a dwa skrajne NG i GM razem
wzięte dają kwadrat z NM większy od podwojonego kwadratu z KG, który
jest równy podwojonemu kwadratowi z AE: więc kwadrat z MN jest większy
od kwadratu z AE i linia NM większa od linii EA, c.b.d.d.
Wniosek
Okazuje się stąd, że odwrotnie, przy ruchu pocisku z punktu końcowego
D, po półparaboli DB, impet osiągnięty jest mniejszy, niż dla każdej
innej wysokości większej lub mniejszej od wysokości półparaboli DB,
której styczna AD czyni z poziomem kąt równy połowie kąta prostego. Stąd
znów wynika, że jeżeli z tym samym impetem wyrzucane będą pociski, z
punktu końcowego D, przy różnych nachyleniach, to rzut najdalej
sięgający, to jest największa amplituda połowy lub całej paraboli,
nastąpi przy nachyleniu równem połowie kąta prostego; inne rzuty, przy
większym lub mniejszym nachyleniu sięgać będą mniej daleko.
SAGREDO: Zadziwiająca i wyborna jest potęga ścisłych dowodzeń, a
takimi są tylko dowodzenia matematyczne. Wiedziałem już
ufając
opowiadaniom wielu bombardierów, że ze wszystkich strzałów armatnich
lub moździerzowych, te, których kula padała najdalej, robione były przy
nachyleniu równym połowie kąta prostego, które oni nazywają szóstym
punktem kwadransa. Ale zrozumienie
przyczyny, skąd to pochodzi, nieskończenie wiele więcej znaczy, niż
proste zapewnienie innych, a nawet więcej niż wielokrotnie powtarzane
doświadczenie.
SALVIATI: Uwaga Waszmości jest nader słuszna: a
poznanie jednego
zjawiska, na zasadzie jego przyczyn, otwiera nam drogę do zrozumienia
innych zjawisk bez potrzeby uciekania się do doświadczeń; tak też rzecz
się ma i w tym przypadku, gdzie przez rozważanie dochodzimy do zdania
sobie sprawy, że najdalszy rzut następuje przy nachyleniu równem połowie
kąta prostego; tu autor dowodzi rzeczy, która
doświadczalnie nie była zaobserwowana a mianowicie, że inne strzały
jednakowo daleko niosą, gdy nachylenia są jednakowo większe lab
mniejsze od połowy kąta prostego: tak, że kule, z których jedna przy nachyleniu 7-go a druga 5-go
punktu kwadransa zostały wystrzelone, dochodzą do poziomu w jednakowej
odległości a także wystrzelone przy nachyleniu 8 i 4, 9 i 3 itd. Ale
wysłuchajmy dowodzenia.
Twierdzenie V. Podanie VIII
Amplitudy parabol, opisanych przez pociski wyrzucone z jednakowym
impetem i przy nachyleniach jednakowo większych lub mniejszych od
połowy kąta prostego są sobie równe.
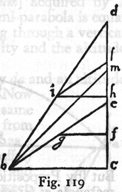 W trójkącie prostokątnym (rys. 119) MCB niech będzie pozioma
BC równa pionowej CM, tak, że kąt MBC jest połową prostego: przedłużmy
CM do D i wykreślmy nad i pod przekątną MB przy wierzchołku B dwa równe
kąty MBE i MBD. Dowieść mamy, że amplitudy parabol opisanych przez
pociski wyrzucone z B z jednakowym impetem, przy nachyleniach EBC i DBC
są sobie równe. Ponieważ bowiem kąt zewnętrzny BMC jest równy
wewnętrznym MDB, DBM, więc tym obu równy jest także kąt MBC. Jeżeli
zamiast kąta DBM weźmiemy kąt MBE, to będzie MBC równy dwu MBE, BDC, a
po odjęciu wspólnego MBE zostanie reszta BDC równa reszcie EBC.
Trójkąty zatem DCB i BCE są podobne. Przepołówmy proste DC i EC w H i F,
poprowadźmy HI, FG równoległe do poziomej CB i jak DH do HI, niech
będzie IH do HL; będzie zatem trójkąt IHL podobny IHD, któremu znów jest
podobny EGF, że zaś IH, GF są równe (bo każda jest połową BC), więc FE,
czyli FC jest równe HL, a dodając do obu FH, otrzymamy CH równe FL.
Jeżeli teraz wyobrazimy sobie połowę paraboli, przechodzącą przez H i
B, o wysokości HC, a wyniosłości HL, to jej amplituda będzie CB, które
jest równe podwojonemu HI, podczas gdy HI jest średnią proporcjonalną
między DH albo CH i HL; styczną więc do niej będzie DB wobec równości
CH i HD. Jeżeli znów wyobrazimy sobie parabolę, przechodzącą przez F i
B, z wyniosłością FL a wysokością FC, między którymi średnią
proporcjonalną jest FG, równe połowie poziomej CB, to tak samo
amplitudą jej będzie CB: styczną zaś do niej jest EB, bo EF i FC są
sobie równe. Ze zaś kąty DBC, EBC (nachylenia rzutu) różnią się
jednakowo od połowy kąta prostego, przeto twierdzenie jest
dowiedzione.
W trójkącie prostokątnym (rys. 119) MCB niech będzie pozioma
BC równa pionowej CM, tak, że kąt MBC jest połową prostego: przedłużmy
CM do D i wykreślmy nad i pod przekątną MB przy wierzchołku B dwa równe
kąty MBE i MBD. Dowieść mamy, że amplitudy parabol opisanych przez
pociski wyrzucone z B z jednakowym impetem, przy nachyleniach EBC i DBC
są sobie równe. Ponieważ bowiem kąt zewnętrzny BMC jest równy
wewnętrznym MDB, DBM, więc tym obu równy jest także kąt MBC. Jeżeli
zamiast kąta DBM weźmiemy kąt MBE, to będzie MBC równy dwu MBE, BDC, a
po odjęciu wspólnego MBE zostanie reszta BDC równa reszcie EBC.
Trójkąty zatem DCB i BCE są podobne. Przepołówmy proste DC i EC w H i F,
poprowadźmy HI, FG równoległe do poziomej CB i jak DH do HI, niech
będzie IH do HL; będzie zatem trójkąt IHL podobny IHD, któremu znów jest
podobny EGF, że zaś IH, GF są równe (bo każda jest połową BC), więc FE,
czyli FC jest równe HL, a dodając do obu FH, otrzymamy CH równe FL.
Jeżeli teraz wyobrazimy sobie połowę paraboli, przechodzącą przez H i
B, o wysokości HC, a wyniosłości HL, to jej amplituda będzie CB, które
jest równe podwojonemu HI, podczas gdy HI jest średnią proporcjonalną
między DH albo CH i HL; styczną więc do niej będzie DB wobec równości
CH i HD. Jeżeli znów wyobrazimy sobie parabolę, przechodzącą przez F i
B, z wyniosłością FL a wysokością FC, między którymi średnią
proporcjonalną jest FG, równe połowie poziomej CB, to tak samo
amplitudą jej będzie CB: styczną zaś do niej jest EB, bo EF i FC są
sobie równe. Ze zaś kąty DBC, EBC (nachylenia rzutu) różnią się
jednakowo od połowy kąta prostego, przeto twierdzenie jest
dowiedzione.
Twierdzenie VI. Podanie IX
Amplitudy dwóch parabol są równe, jeżeli wysokości i wyniosłości
tych parabol są do siebie odwrotnie proporcjonalne.
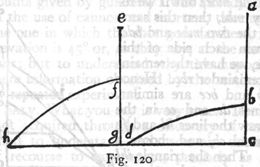 Wysokość (rys. 120) GF paraboli FH ma się do wysokości CB
paraboli BD, jak wyniosłość BA do wyniosłości FE. Twierdzę, że
amplitudy HG i DC są sobie równe. Ponieważ bowiem pierwsza GF ma się do
drugiej CB, jak trzecia BA do czwartej FE, to prostokąt GVE
z pierwszej i czwartej jest równy prostokątowi CBA z
drugiej i trzeciej; zatem kwadraty równe tym prostokątom są sobie równe;
a że prostokątowi GFE jest równy kwadrat z połowy GH, a prostokątowi CBA
kwadrat z połowy CD, to te kwadraty, ich boki i zdwojenia tych boków są
sobie równe. Tymi ostatnimi zaś są amplitudy GH i CD, c.b.d.d.
Wysokość (rys. 120) GF paraboli FH ma się do wysokości CB
paraboli BD, jak wyniosłość BA do wyniosłości FE. Twierdzę, że
amplitudy HG i DC są sobie równe. Ponieważ bowiem pierwsza GF ma się do
drugiej CB, jak trzecia BA do czwartej FE, to prostokąt GVE
z pierwszej i czwartej jest równy prostokątowi CBA z
drugiej i trzeciej; zatem kwadraty równe tym prostokątom są sobie równe;
a że prostokątowi GFE jest równy kwadrat z połowy GH, a prostokątowi CBA
kwadrat z połowy CD, to te kwadraty, ich boki i zdwojenia tych boków są
sobie równe. Tymi ostatnimi zaś są amplitudy GH i CD, c.b.d.d.
Lemat dla następującego twierdzenia
Jeżeli linia prosta podzielona zostanie w jakimkolwiek punkcie na
dwie części, to suma kwadratów ze średnich proporcjonalnych między całą
linią a każdą z części jest równa kwadratowi z całej linii.
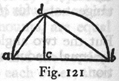 Niech będzie (rys. 121) AB podzielona w C. Twierdzę, że
kwadraty ze średnich proporcjonalnych między całą AB i częściami AC, CB
razem wzięte są równe kwadratowi z całej AB. Opiszmy półkole na AB i
wyprowadźmy z C prostopadłą CD, połączmy DA i DB. Jest więc DA średnią
między BA, AC a DB średnią między AB, BC, a suma kwadratów z linij DA,
BD jest równa kwadratowi z AB, bo kąt ADB w półkolu jest prosty; więc
twierdzenie jest dowiedzione.
Niech będzie (rys. 121) AB podzielona w C. Twierdzę, że
kwadraty ze średnich proporcjonalnych między całą AB i częściami AC, CB
razem wzięte są równe kwadratowi z całej AB. Opiszmy półkole na AB i
wyprowadźmy z C prostopadłą CD, połączmy DA i DB. Jest więc DA średnią
między BA, AC a DB średnią między AB, BC, a suma kwadratów z linij DA,
BD jest równa kwadratowi z AB, bo kąt ADB w półkolu jest prosty; więc
twierdzenie jest dowiedzione.
Twierdzenie VII. Podanie X
Impet czyli moment jakiejkolwiek półparaboli jest równy momentowi
naturalnego spadku wzdłuż prostopadłej do poziomu tak długiej jak suma
wyniosłości i wysokości półparaboli.
 Niech będzie (rys. 122) półparabola AB, której wyniosłością
jest DA, a wysokością AC, z których się składa prostopadła DC. Twierdzę,
że impet na półparaboli w B jest równy momentowi naturalnego spadku od D
do C. Przyjmijmy tę samą DC za miarę czasu i impetu i weźmy średnią
proporcjonalną między CD i CA równą CF. Niech będzie nadto CE średnia
proporcjonalna do DC i CA, to CF jest miarą czasu i momentu spadku
wzdłuż DA ze spoczynku w D, a CE czasem
i momentem spadku wzdłuż AC ze spoczynku w A, zaś przekątna EF momentem
z nich złożonym i to jest właśnie moment na półparaboli w B.
Że zaś DC podzielone jest w A, a CF i CE
są średnie między całym CD a jego częściami DA i AC, to będzie suma
kwadratów z tych średnich, na mocy powyższego lematu, równa kwadratowi z
całości; ale ta suma jest także równa kwadratowi z EF, a więc i linia EF
jest równa DC. Wynika stąd, że momenty spadku po DC i po półparaboli AB
w C i w B są równe, c.b.d.d.
Niech będzie (rys. 122) półparabola AB, której wyniosłością
jest DA, a wysokością AC, z których się składa prostopadła DC. Twierdzę,
że impet na półparaboli w B jest równy momentowi naturalnego spadku od D
do C. Przyjmijmy tę samą DC za miarę czasu i impetu i weźmy średnią
proporcjonalną między CD i CA równą CF. Niech będzie nadto CE średnia
proporcjonalna do DC i CA, to CF jest miarą czasu i momentu spadku
wzdłuż DA ze spoczynku w D, a CE czasem
i momentem spadku wzdłuż AC ze spoczynku w A, zaś przekątna EF momentem
z nich złożonym i to jest właśnie moment na półparaboli w B.
Że zaś DC podzielone jest w A, a CF i CE
są średnie między całym CD a jego częściami DA i AC, to będzie suma
kwadratów z tych średnich, na mocy powyższego lematu, równa kwadratowi z
całości; ale ta suma jest także równa kwadratowi z EF, a więc i linia EF
jest równa DC. Wynika stąd, że momenty spadku po DC i po półparaboli AB
w C i w B są równe, c.b.d.d.
Wniosek
Wynika stąd, że impety wszystkich półparabol, których sumy
wyniosłości i wysokości są równe, są sobie równe.
Zadanie II. Podanie XI
Mając dany impet i amplitudę półparaboli, oznaczyć jej wysokość.
 Niech będzie dany impet (rys. 123), określony długością
prostopadłej do poziomu AB i na poziomej dana amplituda BC. Należy
znaleźć wyniosłość półparaboli, której impet byłby równy AB a amplituda
BC. Z poprzedniego wynika, że połowa amplitudy BC jest średnią
proporcjonalną między wysokością a wyniosłością tejże półparaboli,
której impet według poprzedniego jest równy impetowi spadku wzdłuż AB,
ze spoczynku w A. Zatem AB tak ma być podzielone, aby prostokąt z jego
części był równy kwadratowi z połowy BC czyli z BD. Okazuje się tu, że
DB nie może być większe od połowy BA, bo prostokąt utworzony z części
jest największy, gdy części są równe. Przepołówmy zatem BA w E. Gdyby BD
było równe BE, zadanie byłoby rozwiązane: wysokością półparaboli byłoby
BE, a wyniosłością EA (i oto amplituda paraboli o podniesieniu równym
połowie kąta prostego jest największa, jak to było dowiedzione, ze
wszystkich opisanych przy jednakowym impecie). Gdy znów BD jest mniejsze
od połowy BA, to podzielić należy to ostatnie tak, aby prostokąt z jego
części był równy kwadratowi z DB. Opiszmy półkole na EA, od A odetnijmy
AF równe BD: i poprowadźmy FE, któremu równe odetnijmy EG. Będzie tedy
prostokąt BGA razem z kwadratem z EG równy kwadratowi z EA, któremu
także jest równa suma kwadratów z AF i FE. Jeżeli odejmiemy równe sobie
kwadraty z GE i FE, zostanie prostokąt BGA równy kwadratowi z AF albo z
BD; a linia BD jest średnią proporcjonalną między BG i GA. Wynika stąd,
że wysokość półparaboli o amplitudzie BC i impecie AB jest równa BG a
wyniosłość równa GA. Jeżeli odetniemy BI równe GA, to BI będzie
wysokością, a IA wyniosłością półparaboli IC. Na zasadzie dowiedzionego,
możemy to uczynić.
Niech będzie dany impet (rys. 123), określony długością
prostopadłej do poziomu AB i na poziomej dana amplituda BC. Należy
znaleźć wyniosłość półparaboli, której impet byłby równy AB a amplituda
BC. Z poprzedniego wynika, że połowa amplitudy BC jest średnią
proporcjonalną między wysokością a wyniosłością tejże półparaboli,
której impet według poprzedniego jest równy impetowi spadku wzdłuż AB,
ze spoczynku w A. Zatem AB tak ma być podzielone, aby prostokąt z jego
części był równy kwadratowi z połowy BC czyli z BD. Okazuje się tu, że
DB nie może być większe od połowy BA, bo prostokąt utworzony z części
jest największy, gdy części są równe. Przepołówmy zatem BA w E. Gdyby BD
było równe BE, zadanie byłoby rozwiązane: wysokością półparaboli byłoby
BE, a wyniosłością EA (i oto amplituda paraboli o podniesieniu równym
połowie kąta prostego jest największa, jak to było dowiedzione, ze
wszystkich opisanych przy jednakowym impecie). Gdy znów BD jest mniejsze
od połowy BA, to podzielić należy to ostatnie tak, aby prostokąt z jego
części był równy kwadratowi z DB. Opiszmy półkole na EA, od A odetnijmy
AF równe BD: i poprowadźmy FE, któremu równe odetnijmy EG. Będzie tedy
prostokąt BGA razem z kwadratem z EG równy kwadratowi z EA, któremu
także jest równa suma kwadratów z AF i FE. Jeżeli odejmiemy równe sobie
kwadraty z GE i FE, zostanie prostokąt BGA równy kwadratowi z AF albo z
BD; a linia BD jest średnią proporcjonalną między BG i GA. Wynika stąd,
że wysokość półparaboli o amplitudzie BC i impecie AB jest równa BG a
wyniosłość równa GA. Jeżeli odetniemy BI równe GA, to BI będzie
wysokością, a IA wyniosłością półparaboli IC. Na zasadzie dowiedzionego,
możemy to uczynić.
Zadanie III. Podanie XII
Obliczyć i zestawić w tablicy amplitudy wszystkich półparabol,
opisanych przez pociski wyrzucone z jednakowym impetem.
 Z poprzednio dowiedzionego wynika, że pociski z jednakowym impetem
wyrzucane, opisywać będą parabole, których sumy wyniosłości i wysokości
będą jednakowe. Wszystkie te sumy leżą przeto na pionowej zawartej między
temi samymi dwiema poziomymi. Niech będzie (rys. 124) do
poziomej CB prostopadła równa jej BA i poprowadźmy przekątną AC. Kąt ACB
będzie zatem połową prostego czyli 45 stopni. Przepołówmy prostopadłą
BA w D, to będzie DC tą półparabolą, która ma wyniosłość AD, a wysokość
DB; a jej impet w C jest ten sam, jak ciała spadającego ze spoczynku w
A wzdłuż AB, w punkcie B. Poprowadźmy AG równoległe do BC; dla
wszystkich innych półparabol tegoż samego impetu winny sumy wyniosłości
i wysokości mieścić się między AG i BC. Ponieważ dalej dowiedzione
zostało, że amplitudy tych półparabol, których styczne jednakowo nad lub
pod 45 stopniem są skierowane, są sobie równe, więc rachunek
przeprowadzony dla większych nachyleń służyć będzie i dla mniejszych.
Przyjmijmy także liczbę dziesięciu tysięcy części, jako największą
amplitudę półparaboli opisanej rzutem przy nachyleniu 45°, taka więc
będą linia BA i amplituda półparaboli BC. Obieramy zaś liczbę 10000,
bo użyjemy do rachunku tablicy stycznych, która daje tę liczbę jako
styczną kąta 45 stopni. Przystępując do dzieła, poprowadźmy CE pod kątem
ECB większym od kąta ACB (ale zawsze ostrym): mamy nakreślić półparabolę styczną do linii EC, której wyniosłość
razem z wysokością ma być równa AB. Z tablicy stycznych weźmiemy
długość stycznej BE kąta BCE i ta długość przepołowiona da nam punkt F.
Określamy następnie trzecią proporcjonalną do BF i do BI (połowy BC),
która koniecznie będzie większa od FA. Niech nią będzie FO.
Dla półparaboli więc wpisanej w trójkąt ECB, ze styczną CE i amplitudą
CB, otrzymujemy wysokość BF i wyniosłość FO. Ale suma BO przewyższa
odległość między równoległymi AG i BC, a tymczasem parabole nie mogą
przekraczać tych granic, gdyż tak szukana, jak i parabola DC opisywane są
pociskami wyrzucanymi z C z tym samym impetem. Szukać więc należy innej
paraboli, podobnej do znalezionej (bo pod kątem BCE mogą być opisane
niezliczone podobne do siebie większe lub mniejsze), której suma
wyniosłości i wysokości jest równa BA. Niech się więc ma OB do BA jak
amplituda BC do CR i otrzymamy CR amplitudę półparaboli opisanej przy
nachyleniu kąta BCE, której suma wyniosłości i wysokości mieści się
między poziomem! GA i CB, co właśnie było żądane. Postępowanie zatem
będzie takie.
Z poprzednio dowiedzionego wynika, że pociski z jednakowym impetem
wyrzucane, opisywać będą parabole, których sumy wyniosłości i wysokości
będą jednakowe. Wszystkie te sumy leżą przeto na pionowej zawartej między
temi samymi dwiema poziomymi. Niech będzie (rys. 124) do
poziomej CB prostopadła równa jej BA i poprowadźmy przekątną AC. Kąt ACB
będzie zatem połową prostego czyli 45 stopni. Przepołówmy prostopadłą
BA w D, to będzie DC tą półparabolą, która ma wyniosłość AD, a wysokość
DB; a jej impet w C jest ten sam, jak ciała spadającego ze spoczynku w
A wzdłuż AB, w punkcie B. Poprowadźmy AG równoległe do BC; dla
wszystkich innych półparabol tegoż samego impetu winny sumy wyniosłości
i wysokości mieścić się między AG i BC. Ponieważ dalej dowiedzione
zostało, że amplitudy tych półparabol, których styczne jednakowo nad lub
pod 45 stopniem są skierowane, są sobie równe, więc rachunek
przeprowadzony dla większych nachyleń służyć będzie i dla mniejszych.
Przyjmijmy także liczbę dziesięciu tysięcy części, jako największą
amplitudę półparaboli opisanej rzutem przy nachyleniu 45°, taka więc
będą linia BA i amplituda półparaboli BC. Obieramy zaś liczbę 10000,
bo użyjemy do rachunku tablicy stycznych, która daje tę liczbę jako
styczną kąta 45 stopni. Przystępując do dzieła, poprowadźmy CE pod kątem
ECB większym od kąta ACB (ale zawsze ostrym): mamy nakreślić półparabolę styczną do linii EC, której wyniosłość
razem z wysokością ma być równa AB. Z tablicy stycznych weźmiemy
długość stycznej BE kąta BCE i ta długość przepołowiona da nam punkt F.
Określamy następnie trzecią proporcjonalną do BF i do BI (połowy BC),
która koniecznie będzie większa od FA. Niech nią będzie FO.
Dla półparaboli więc wpisanej w trójkąt ECB, ze styczną CE i amplitudą
CB, otrzymujemy wysokość BF i wyniosłość FO. Ale suma BO przewyższa
odległość między równoległymi AG i BC, a tymczasem parabole nie mogą
przekraczać tych granic, gdyż tak szukana, jak i parabola DC opisywane są
pociskami wyrzucanymi z C z tym samym impetem. Szukać więc należy innej
paraboli, podobnej do znalezionej (bo pod kątem BCE mogą być opisane
niezliczone podobne do siebie większe lub mniejsze), której suma
wyniosłości i wysokości jest równa BA. Niech się więc ma OB do BA jak
amplituda BC do CR i otrzymamy CR amplitudę półparaboli opisanej przy
nachyleniu kąta BCE, której suma wyniosłości i wysokości mieści się
między poziomem! GA i CB, co właśnie było żądane. Postępowanie zatem
będzie takie.
Wziąwszy styczną danego kąta BCE, przepoławia się ją i do tej połowy
oraz do połowy BC znajduje się trzecią proporcjonalną, którą jest FO.
Niech będzie dalej jak OB do BA, tak BC do tej ruchomej amplitudy CR.
Weźmy przykład.
Niech kąt ECB ma 50 stopni, styczna jego będzie 11918, a jej połowa BF
5959, połowa BC 5000, trzecia proporcjonalna do obu tych połów 4195,
które dodane do BF daje 10154 jako BO. Jak więc OB do BA, czyli jak
10154 do 10000, tak będzie BC, czyli 10000 (obie bowiem są stycznemi
kąta 45 stopni) do innej i otrzymamy ruchomą amplitudę BC 9848, podczas
gdy BC (największa amplituda) wynosi 10000. Amplitudy całych parabol
wynosić będą dwa razy tyle 19696 i 20000. Równie wielka jest amplituda
paraboli przy nachyleniu 40 stopni, bo to nachylenie na tyleż się różni
od 45 stopni.
SAGREDO: Aby dobrze zrozumieć to dowodzenie, brak mi wiadomości,
dlaczego trzecia proporcjonalna do BF i BI ma być (jak mówi autor)
koniecznie większa od FA.
SALVIATI: Wniosek ten, jak mi się zdaje, wywiedziony może być w ten
sposób. Kwadrat ze średniej z trzech linii proporcjonalnych jest równy
prostokątowi z dwóch skrajnych, a więc kwadrat z BI albo z równej do
niej BD jest równy prostokątowi z pierwszej skrajnej FB i drugiej, którą
należy znaleźć; ta druga skrajna musi być koniecznie większa od FA, bo
prostokąt BF na FA jest mniejszy od kwadratu z BD i to właśnie o kwadrat
z DF, jak to dowiódł Euklides. Zauważyć należy również, że punkt F,
przepoławiający styczną EB, znajdować się będzie w wielu razach ponad
punktem A, a raz tylko w tymże punkcie A; w tym zaś przypadku oczywiście
cała trzecia proporcjonalna do połowy stycznej i do BI dającej
wyniosłość leżeć będzie ponad A. Lecz autor wybrał taki przypadek,
kiedy nie było oczywiste, że wzmiankowana trzecia proporcjonalna będzie
zawsze większa od FA i że przewyżka ponad F przekroczy równoległą AG.
Ale idźmy dalej.
Dobrze by było przy pomocy tej tablicy ułożyć drugą uzupełniającą,
dla wysokości takichże półparabol, opisanych z tym samym impetem.
Postępowanie będzie następujące.
Zadanie IV. Podanie XIII
Z danych w następującej tablicy amplitud półparabol, przy
zachowaniu wspólnego impetu, z jakim każda z nich została opisana,
oznaczyć wysokość poszczególnych półparabol.
 Niech będzie (rys. 125) dana amplituda BC. Impet zaś, który
przyjmujemy, że jest wciąż jednakowy, niech będzie OB, jest to suma
wysokości i wyniosłości. Mamy oznaczyć i wydzielić samą wysokość.
Ponieważ BO ma być tak podzielone, aby prostokąt z jego części był
równy kwadratowi z połowy amplitudy BC, to punkt podziału przypadnie w
F. Przepołówmy OB i BC w D i I. Kwadrat więc z IB jest równy
prostokątowi BFO, podczas gdy kwadrat z DO równy jest temuż prostokątowi
razem z kwadratem z FD. Jeżeli zatem od kwadratu z DO odejmiemy kwadrat
z BI, równy prostokątowi BFO, to pozostanie kwadrat z FD, a dodawszy do
jego boku FD długość BD, otrzymamy szukaną wysokość BF. Postępuje się
zatem w ten sposób. Od kwadratu z połowy BO odejmuje się kwadrat z BI, z
reszty wyciąga się pierwiastek kwadratowy, dodaje do niego BD i
otrzymuje szukaną wysokość BF. Przykład. Szukamy wysokościpółparaboli
opisanej przy 55 stopniach podniesienia. Amplituda z poprzedniej
tablicy jest 9396, połowa jej 4698, a kwadrat z tej połowy 22071204; to
odjęte od kwadratu z połowy BA, który jest zawsze jednaki, mianowicie
25000000, daje resztę 2928796, z której pierwiastek kwadratowy wynosi
prawie 1710. Dodany do połowy BA, to jest do 5000, daje 6710 i taka jest
wysokość BF. Nie będzie zbyteczne' ułożenie trzeciej tablicy,
zawierającej wysokości i wyniosłości półparabol, mających jednakową
amplitudę.
Niech będzie (rys. 125) dana amplituda BC. Impet zaś, który
przyjmujemy, że jest wciąż jednakowy, niech będzie OB, jest to suma
wysokości i wyniosłości. Mamy oznaczyć i wydzielić samą wysokość.
Ponieważ BO ma być tak podzielone, aby prostokąt z jego części był
równy kwadratowi z połowy amplitudy BC, to punkt podziału przypadnie w
F. Przepołówmy OB i BC w D i I. Kwadrat więc z IB jest równy
prostokątowi BFO, podczas gdy kwadrat z DO równy jest temuż prostokątowi
razem z kwadratem z FD. Jeżeli zatem od kwadratu z DO odejmiemy kwadrat
z BI, równy prostokątowi BFO, to pozostanie kwadrat z FD, a dodawszy do
jego boku FD długość BD, otrzymamy szukaną wysokość BF. Postępuje się
zatem w ten sposób. Od kwadratu z połowy BO odejmuje się kwadrat z BI, z
reszty wyciąga się pierwiastek kwadratowy, dodaje do niego BD i
otrzymuje szukaną wysokość BF. Przykład. Szukamy wysokościpółparaboli
opisanej przy 55 stopniach podniesienia. Amplituda z poprzedniej
tablicy jest 9396, połowa jej 4698, a kwadrat z tej połowy 22071204; to
odjęte od kwadratu z połowy BA, który jest zawsze jednaki, mianowicie
25000000, daje resztę 2928796, z której pierwiastek kwadratowy wynosi
prawie 1710. Dodany do połowy BA, to jest do 5000, daje 6710 i taka jest
wysokość BF. Nie będzie zbyteczne' ułożenie trzeciej tablicy,
zawierającej wysokości i wyniosłości półparabol, mających jednakową
amplitudę.
SAGREDO: Tę ostatnią pragnąłbym widzieć, bo z niej mógłbym się
dowiedzieć o różnicy w impecie i sile przy jednakowej nośności
strzałów, która to różnica musi być bardzo wielka dla różnych podniesień
i tak np. przy wyrzucaniu kuli pod nachyleniem 3 lub 4 albo 87 lub 88
stopni, na odległość taką, jak przy nachyleniu 45 stopni (w którym to
przypadku wystarcza najmniejszy impet), znalezionoby niezmierną
przewyżkę siły.
SALVIATI: Waszmość ma zupełną rację i przekona się, że
aby wyśledzić działanie, trzeba wielkimi liczbami iść ku nieskończonymu
impetowi. Ale przyjrzyjmy się układowi tablicy.
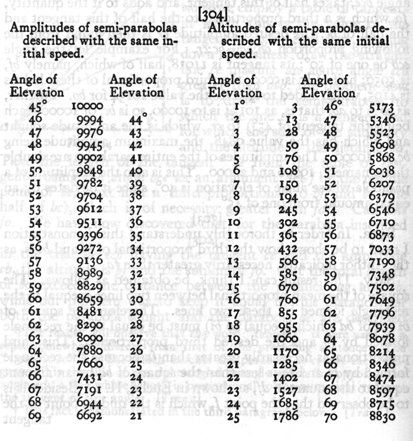
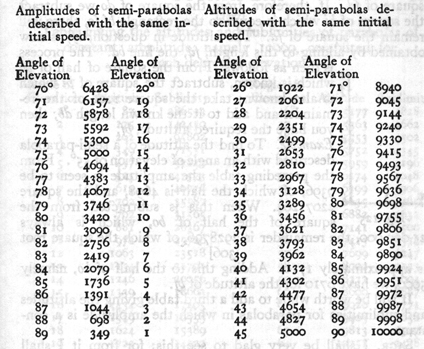 Zadanie V. Podanie XIV
Zadanie V. Podanie XIV
Znaleźć, dla różnych podniesień, wysokości i wyniosłości półparabol
jednakowej amplitudy.
Łatwo rozwiązać to zadanie. Jeżeli bowiem przyjmiemy stałą amplitudę
półparaboli równą 10000 częściom, to połowa stycznej któregokolwiek
stopnia podniesienia wyrażać będzie wysokość. Gdy np. amplituda
półparaboli o podniesieniu 30 stopni wynosi 10000, to wysokość jej
będzie 2887, bo tyle prawie wynosi połowa stycznej. Mając wysokość
otrzymamy wyniosłość w ten sposób. Ponieważ dowiedziono, że połowa
amplitudy półparaboli jest średnią proporcjonalną między wysokością a
wyniosłością, a znaną już jest wysokość, i połowa amplitudy wynosi stale
5000, należy więc kwadrat z ostatniej wielkości podzielić przez
wysokość, a iloraz da wyniosłość. I tak w przykładzie. Wysokość znaleziono 2887, kwadrat z
5000 wynosi 25000000, co podzielone przez 2887 daje prawie 8659 jako
szukaną wyniosłość.
SALVIATI: Widzimy tu najpierw jak prawdziwą jest
powyższa uwaga, według której przy różnych podniesieniach, im się ono
więcej odchyla w górę lub na dół od średniego, tym większego trzeba
impetu i siły, aby rzucić pocisk na tę samą odległość. Albowiem impet z dwóch ruchów się
składa, jednostajnego poziomego i przyspieszonego prostopadłego i ten
impet staje się miarą sumy wysokości i wyniosłości, a ta suma, jak
widzimy w podanej tablicy, jest najmniejsza przy 45 stopniach
podniesienia, gdy wysokość i wyniosłość są sobie równe, wynoszą każda 5000, a suma ich 10000. Przy
innym podniesieniu np. 50 stopni, otrzymamy wysokość 5959, wyniosłość
4196, a sumę obu 10155. I takiż będzie impet przy 40 stopniach, gdyż to
podniesienie jest tak samo oddalone od środkowego. Zaznaczyć przeto
należy, że wszystkie impety są równe sobie parami, przy podniesieniach
jednakowo oddalonych od środkowego, z tą piękną odmianą, że wysokość i
wyniosłość przy podniesieniach większych odpowiadają na odwrót
wyniosłości i wysokości przy mniejszych; tak że podczas gdy przy 50
stopniach mamy wysokość 5959 a wyniosłość 4196, to odwrotnie przy 40
stopniach otrzymamy wysokość 4196 a wyniosłość 5959 i tak samo dla
wszystkich innych bez żadnego wyjątku. W rachunku opuszczone zostały
ułamki, nie mające znaczenia przy wielkich liczbach.
SAGREDO: Zauważę przy tym, że z dwóch impetów, poziomego i
prostopadłego, im wyższe będą rzuty, tym mniejszy okaże się poziomy. a
tym większy prostopadły. Przeciwnie, przy małym podniesieniu, potrzeba
wielkiej siły impetu poziomego przy małej wysokości spadku pocisku. I,
jeżeli dobrze rozumiem, że przy całkowitym podniesieniu do 90 stopni,
żadna siła na świecie nie wystarczy, aby rzucić pocisk na jeden cal
odległości od prostopadłej; lecz pocisk spadnie koniecznie na to
miejsce, z którego został wyrzucony, to znów nie mógłbym z tą samą
pewnością twierdzić, że przy podniesieniu zero stopni, tj. po linii
poziomej nie można by z pewną skończoną siłą rzucić pocisku na pewną
odległość. I tak np. nawet śmigownica nie zdołałaby kuli żelaznej
wyrzucić poziomo, czyli, jak się mówi, z białego punktu (di punto
blanco), tj. bez żadnego podniesienia. Twierdzę, że w tym przypadku
pozostaje pewna wątpliwość i nie przeczę stanowczo faktowi, gdyż
wstrzymuje mnie inny przypadek, nie mniej godny podziwu, którego
posiadam stanowczy dowód. A przypadek ten polega na niemożności
absolutnie prostego wyciągnięcia liny, równolegle do poziomu; wygina
się ona zawsze i żadną siłą nie można jej wyprostować.
SALVIATI: A więc, mości Sagredo, w tym
przypadku ustaje pański podziw tego cudownego skutku, skoro pan posiada
dowód. Badając wszakże uważnie, znajdziemy może pewną analogię między
przypadkami pocisku i liny. Krzywizna linii rzutu poziomego pochodzi od
dwóch sił, z których jedna (siła rzutu) działa poziomo, podczas gdy
druga (ciężkość pocisku), działa w kierunku do tamtej prostopadłym. Ale
przy wyciąganiu liny działają także dwie siły, pozioma rozciągająca i
ciężar liny działający do nią prostopadle. Dość więc podobne są oba
przypadki. I skoro pan przyznaje ciężarowi liny tyle potęgi i energii,
aby mógł przeciwważać i przezwyciężać jakąkolwiek niezmienną siłę, to
dlaczegóż odmawia pan tego ciężarowi kuli? Albo, powiedziałbym lepiej
jeszcze, dziwi nas i sprawia nam przyjemność, gdy lina, mocno lub słabo
rozciągana, wygina się według linii zbliżonej do paraboli, a to
podobieństwo jest tak wielkie, ze jeżeli narysujemy na powierzchni
płaskiej, postawionej prostopadle do poziomu, linię paraboliczną i
trzymać ją będziemy odwrotnie, tj. zwróconą wierzchołkiem do spodu, a
podstawą równoległą do poziomu, i jeżeli przyłożymy cienki łańcuszek
utrzymyway na końcach podstawy narysowanej paraboli, to zobaczymy, że
się ten łańcuszek ugina i schodzi z tą parabolą; a to schodzenie się
tym będzie dokładniejsze, im parabola mniejszą ma krzywinzę, czyli
więcej jest rozciągnięta, tak że przy paraboli opisanej z podniesieniem
45 stopni, łańcuch dokładnie (quasi ad unguem) zakrywa parabolę.
SAGREDO: Można by przeto takim
łańcuszkiem, subtelnie wykonanym, wyznaczać szybko na powierzchni
płaskiej wiele parabol.
SALVIATI: Można by i to z niemałym pożytkiem, jak o tym zaraz powiem.
SIMPLICIO: Ale zanim pójdziemy dalej, pragnąłbym przekonać się o
ścisłości twierdzenia, które podajecie jako stanowczo dowiedzione,
mianowicie, że jest niemożebne, z największą nawet siłą, rozciągnąć liny
zupełnie prosto, równolegle do poziomu.
SAGREDO : Postaram się przypomnieć sobie ten dowód, dla
zrozumienia którego trzeba, aby p. Simplicio przyjął za rzecz pewną to,
co zostało ustalone we wszystkich maszynach, nie tylko doświadczeniem,
lecz i teoretycznymi wywodami, mianowicie że nawet najmniejsza prędkość
ciała poruszającego jest w stanie przemóc choćby bardzo wielki opór
ciała poruszanego, które będzie się wolno poruszać, gdy tylko stosunek
prędkości poruszającego do powolności poruszanego będzie większy od
stosunku oporu ciała poruszanego do siły poruszającego.
SIMPLICIO: Jest mi to dobrze znane, i dowiedzione zostało przez
Arystotelesa w jego zadaniach mechanicznych. Spostrzega się to wyraźnie
na drągu, na przezmianie, którego ciężar ruchomy waży tylko 4 funty, a
podnosi ciężar 400, gdy tylko odległość ciężaru ruchomego od środka,
około którego przezmian się obraca, jest więcej niż sto razy większa od
odległości punktu zawieszenia większego ciężaru; a pochodzi to stąd, że
ciężar ruchomy, obniżając się, przebywa drogę sto razy większą od
drogi, po której się równocześnie podnosi wielki ciężar. Innymi słowy,
mały ciężar ruchomy porusza się ze sto razy większą prędkością od
wielkiego ciężaru.
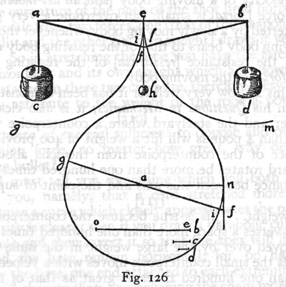 SAGREDO : Wybornie rozumujecie i przyznacie niewątpliwie, że
jakkolwiek mała będzie siła ciała poruszającego, to jednak pokona jak
największy opór, skoro tylko powiększenie prędkości przewyższy ubytek
siły i ciężkości. Ale przejdźmy do przypadku liny. A objaśniając na
rysunku, (rys. 124) niech linę przedstawia linia AB,
przechodząca przez dwa punkty stałe AB, na której końcach są zawieszone
wielkie ciężary C, D, które ciągnąc z wielką siłą utrzymają linę
wyciągniętą prosto, o ile przyjmujemy ją jako nieważką. Lecz jeżeli w
jej środkowym punkcie E zawiesimy jakikolwiek mały ciężar H, to linia
AB się ugnie i zejdzie do F, a wydłużając się wskutek tego zmusi do
podniesienia się dwa wielkie ciężary C, D: co w ten sposób może być
dowiedzione. Z punktów A i B, jako środków, opisujemy dwie ćwiartki koła
EFG i ELM; a ponieważ promienie AI i BL są równe AE i EB, to FI i FL będą
wydłużeniami tj. przewyżkami AF i FB ponad AE i EB; one zatem
wyznaczają podniesienia ciężarów C i D, gdy ciężar H zdoła obniżyć linę
do F, to zaś może nastąpić wtedy, gdy stosunek linii EF, tj. obniżenia
ciężaru H, do linii FI określającej podniesienie ciężarów C i D, będzie
większy od stosunku obu ciężarów C i D do ciężaru H. Ale to nastąpi
koniecznie, chociażby ciężary C i D były jak największe, a ciężar H jak
najmniejszy. Albowiem przewyżka C i D nad H nie jest tak wielka, aby nie
mogła być przedstawiona przez przewyżkę stycznej EF nad kawałkiem
siecznej FI. O tym zaś przekonamy się w tym sposób: niech będzie koło o
średnicy GI i jaki jest stosunek ciężarów C i D do ciężaru H, taki niech
będzie stosunek BO do innej linii C, większej od D, tak że stosunek BO
do D będzie większy od stosunku BO do C; weźmy następnie trzecią
proporcjonalną do OB i D, mianowicie BE i jak OE do EB, tak niech się ma
średnica GI do przedłużenia IF, a przez koniec F poprowadźmy styczną
FN. A ponieważ tak się ma OE do EB, jak GI do FI, to
będzie się miała suma OB do BE, jak GF do FI. Ale między OB i BE średnią
proporcjonalną jest D, a między GF i FI średnią jest NF; więc tak się ma
NF do FI, jak OB do D i stosunek ten jest większy od stosunku ciężarów
C i D do H. Stosunek więc obniżenia, czyli prędkości ciężaru H, do
podniesienia, czyli prędkości ciężarów C i D, jest większy od stosunku
ciężarów C i D do ciężaru H; zatem H musi się obniżać, a linia AB
odchylać od prostej poziomej. Co zaś dzieje się z nieważką liną AB przy
malym obciążeniu w B, to stanie się z ciężką liną bez dodawania innego
ciężaru, gdyż zawieszony zostaje ciężar tworzywa samej liny AB.
SAGREDO : Wybornie rozumujecie i przyznacie niewątpliwie, że
jakkolwiek mała będzie siła ciała poruszającego, to jednak pokona jak
największy opór, skoro tylko powiększenie prędkości przewyższy ubytek
siły i ciężkości. Ale przejdźmy do przypadku liny. A objaśniając na
rysunku, (rys. 124) niech linę przedstawia linia AB,
przechodząca przez dwa punkty stałe AB, na której końcach są zawieszone
wielkie ciężary C, D, które ciągnąc z wielką siłą utrzymają linę
wyciągniętą prosto, o ile przyjmujemy ją jako nieważką. Lecz jeżeli w
jej środkowym punkcie E zawiesimy jakikolwiek mały ciężar H, to linia
AB się ugnie i zejdzie do F, a wydłużając się wskutek tego zmusi do
podniesienia się dwa wielkie ciężary C, D: co w ten sposób może być
dowiedzione. Z punktów A i B, jako środków, opisujemy dwie ćwiartki koła
EFG i ELM; a ponieważ promienie AI i BL są równe AE i EB, to FI i FL będą
wydłużeniami tj. przewyżkami AF i FB ponad AE i EB; one zatem
wyznaczają podniesienia ciężarów C i D, gdy ciężar H zdoła obniżyć linę
do F, to zaś może nastąpić wtedy, gdy stosunek linii EF, tj. obniżenia
ciężaru H, do linii FI określającej podniesienie ciężarów C i D, będzie
większy od stosunku obu ciężarów C i D do ciężaru H. Ale to nastąpi
koniecznie, chociażby ciężary C i D były jak największe, a ciężar H jak
najmniejszy. Albowiem przewyżka C i D nad H nie jest tak wielka, aby nie
mogła być przedstawiona przez przewyżkę stycznej EF nad kawałkiem
siecznej FI. O tym zaś przekonamy się w tym sposób: niech będzie koło o
średnicy GI i jaki jest stosunek ciężarów C i D do ciężaru H, taki niech
będzie stosunek BO do innej linii C, większej od D, tak że stosunek BO
do D będzie większy od stosunku BO do C; weźmy następnie trzecią
proporcjonalną do OB i D, mianowicie BE i jak OE do EB, tak niech się ma
średnica GI do przedłużenia IF, a przez koniec F poprowadźmy styczną
FN. A ponieważ tak się ma OE do EB, jak GI do FI, to
będzie się miała suma OB do BE, jak GF do FI. Ale między OB i BE średnią
proporcjonalną jest D, a między GF i FI średnią jest NF; więc tak się ma
NF do FI, jak OB do D i stosunek ten jest większy od stosunku ciężarów
C i D do H. Stosunek więc obniżenia, czyli prędkości ciężaru H, do
podniesienia, czyli prędkości ciężarów C i D, jest większy od stosunku
ciężarów C i D do ciężaru H; zatem H musi się obniżać, a linia AB
odchylać od prostej poziomej. Co zaś dzieje się z nieważką liną AB przy
malym obciążeniu w B, to stanie się z ciężką liną bez dodawania innego
ciężaru, gdyż zawieszony zostaje ciężar tworzywa samej liny AB.
SIMPLICIO: Zaspokojony jestem zupełnie; a może p. Salviati, stosownie
do obietnicy, zechce objaśnić nam pożytek, jaki możemy wyciągnąć z
łańcuszka i jednocześnie zakomunikować nam poglądy naszego akademika na
siłę uderzenia (forza della percossa).
SALVIATI: Dzień nam zajęły przeprowadzone rozważania, a godzina jest
już trochę późna i nie starczyłaby na wyczerpanie wzmiankowanych
przedmiotów; odłóżmy przeto rozprawy do innej sposobniejszej chwili.
SAGREDO : Godzę się na to z Waszmością, gdyż przekonałem się z
różnych rozmów z zaufanymi przyjaciółmi naszego Akademika, że przedmiot
ten jest bardzo ciemny i nikomu z traktujących o nim dawniej nie udało
się zbadać jego tajników, dalekich od zwykłych wyobrażeń; a najdziwniejsze wydaje mi się to, że siła uderzenia jest nieoznaczona, jeżeli
nie nieskończenie wielka. Czekać więc będziemy na sposobność pana
Salviati. Tymczasem prosiłbym o wiadomość, co teraz następuje w
traktacie o pociskach.
SALVIATI: Są tam jeszcze niektóre twierdzenia o środku ciężkości
brył, wywiedzione przez naszego Akademika w jego młodych latach, które
jak się zdaje, w traktacie, jaki napisał Federigo Comandino,
przedstawiały pewne niedokładności. Sądził on, że przez te podania,
które zobaczycie napisane, będzie mógł zastąpić to, czego szukał w
książce Comandina, a zajął się tym rozważaniem na żądanie prześwietnego
margrabiego Guid'Ubaldo del Monte, znakomitego matematyka swego czasu,
jak to wykazują różne ogłoszone jego dzieła; temu to panu doręczył
odpis i zamierzał rozciągnąć badanie na bryły, którymi się nie zajmował
Comandino, ale gdy później znalazł ten sam przedmiot w książce wielkiego
geometry pana Luca Valerio i przekonał się, że tenże cały ten przedmiot
bez żadnego pominięcia opracował, wtedy przestał się tym zajmować,
chociaż co do metody inaczej niż Valerio przedmiot traktował.
SAGREDO: Dobrze więc będzie, aby na czas, jaki upłynie do naszego
następnego spotkania, Waszmość zostawił mi książkę, dla przejrzenia i
przestudiowania tych podań, jak są napisane.
SALVIATI: Czynię zadość życzeniu Waszmości i spodziewam się, że
podania będą się Wam podobały.
Koniec dnia czwartego.
DODATEK
Wydanie Rozmów i dowodzeń matematycznych z
1638 zawierało jeszcze, na stronach 289-305 Appendix, poświęcony
zagadnieniom matematycznym.
Wydanie polskie z 1930 zawierało też rozmowy z Dnia Piątego i
Szóstego, ogłoszone już po śmierci Galileusza.
deklaracja dostępności
 SALVIATI: Jestem na usługi Waszmościów, jeżeli tylko zdołam sobie
przypomnieć wszystko, czego się nauczyłem od naszego Akademika, który
wiele rozmyślał o tych rzeczach i zawsze na podstawie swojej metody
geometrycznej, tak że nie bez racji możnaby to nazwać nową
umiejętnością. Więc, jakkolwiek niektóre zasady przez innych, a
najpierw przez Arystotelesa były wywiedzione, to jednak tu są
najpiękniejsze i najcenniejsze niewątpliwie podstawy ze wszystkiemi
dowodzeniami. Tymi też mogę was przekonać i nie potrzebuję zajmować was
rzeczami prawdopodobnymi, gdyż początki mechaniki są wam znane, o ile
się na nich trzeba będzie opierać. Przede wszystkiem rozpatrzmy co się
dzieje, gdy łamiemy kawałek drzewa, lub jakieś inne ciało, którego
cząstki mocno są ze sobą związane, gdyż tu znajdziemy pierwszą i
najprostszą zasadę, na której wszystko polega. Dla lepszego
zrozumienia bierzemy pod uwagę (rys. 1) walec lub
graniastosłup AB, z drzewa lub innego materiału, mocnego i spójnego,
umocowany swym górnym końcem w A, wiszący pionowo i obciążony u spodu
ciężarem C. Jakakolwiek jest jego wytrzymałość i spójność
międzycząsteczkowa, byleby tylko nie była nieskończona, to można ją
zawsze pokonać ciężarem C, jeżeli przypuścimy, że ten ciężar można
dowolnie powiększać, tak że walec zostanie rozerwany, jak powróz. A tak
jak w powrozie przypuszczamy, że wytrzymałość pochodzi z włókien, z
których lina się składa, to również drzewo składa się z włókien,
mianowicie z długich słojów, które czynią drzewo wytrzymałym na
rozerwanie w większym stopniu, niż włókna powrozu tej samej grubości. W
walcu kamiennym lub metalowym wytrzymałość zależy od innego środka,
wiążącego cząstki jedne z drugimi, ale i taki walec się rozrywa przy
mocnem rozciąganiu.
SALVIATI: Jestem na usługi Waszmościów, jeżeli tylko zdołam sobie
przypomnieć wszystko, czego się nauczyłem od naszego Akademika, który
wiele rozmyślał o tych rzeczach i zawsze na podstawie swojej metody
geometrycznej, tak że nie bez racji możnaby to nazwać nową
umiejętnością. Więc, jakkolwiek niektóre zasady przez innych, a
najpierw przez Arystotelesa były wywiedzione, to jednak tu są
najpiękniejsze i najcenniejsze niewątpliwie podstawy ze wszystkiemi
dowodzeniami. Tymi też mogę was przekonać i nie potrzebuję zajmować was
rzeczami prawdopodobnymi, gdyż początki mechaniki są wam znane, o ile
się na nich trzeba będzie opierać. Przede wszystkiem rozpatrzmy co się
dzieje, gdy łamiemy kawałek drzewa, lub jakieś inne ciało, którego
cząstki mocno są ze sobą związane, gdyż tu znajdziemy pierwszą i
najprostszą zasadę, na której wszystko polega. Dla lepszego
zrozumienia bierzemy pod uwagę (rys. 1) walec lub
graniastosłup AB, z drzewa lub innego materiału, mocnego i spójnego,
umocowany swym górnym końcem w A, wiszący pionowo i obciążony u spodu
ciężarem C. Jakakolwiek jest jego wytrzymałość i spójność
międzycząsteczkowa, byleby tylko nie była nieskończona, to można ją
zawsze pokonać ciężarem C, jeżeli przypuścimy, że ten ciężar można
dowolnie powiększać, tak że walec zostanie rozerwany, jak powróz. A tak
jak w powrozie przypuszczamy, że wytrzymałość pochodzi z włókien, z
których lina się składa, to również drzewo składa się z włókien,
mianowicie z długich słojów, które czynią drzewo wytrzymałym na
rozerwanie w większym stopniu, niż włókna powrozu tej samej grubości. W
walcu kamiennym lub metalowym wytrzymałość zależy od innego środka,
wiążącego cząstki jedne z drugimi, ale i taki walec się rozrywa przy
mocnem rozciąganiu. SALVIATI: Bądźcie więc dobrej myśli. Zakomunikować Wam pragnę, w
jaki sposób potęga próżni może być oddzielona od innych sił i jak ją
można zmierzyć. Dla jej wyosobnienia weźmy pod uwagę ciało, które sile
dążącej do rozerwania jego cząstek nie stawia innego oporu jak tylko
próżnię, a nasz akademik dowiódł w swoim traktacie, że takim ciałem
właśnie jest woda. Jeżeli więc tak umieścimy walec z wody, aby można
było wykazać jego wytrzymałość na rozerwanie, to ta wytrzymałość nie
będzie miała innej przyczyny, jak tylko opór stawiany przez próżnię.
Dla wykonania takiego doświadczenia obmyśliłem przyrząd, który
rysunkiem łatwiej niż słowami mogę wam przedstawić. Niech będzie CABD
(rys. 4) przekrój cylindra metalowego lub szklanego, którego
wnętrze byłoby jak najregularniej obtoczone i do tego wnętrza przylegał
ściśle wałek pełny z drzewa EFGH, mogący się posuwać w cylindrze i mający w środku otwór, przez który przechodzi zatyczka żelazna,
zakrzywiona u spodu K, a mająca na wierzchu zgrubienie ostro-kręgowe l,
zamykające ściśle lejkowaty wierzch otworu w wałku pełnym, gdy zatyczka
pociągnięta zostanie do dołu. W cylindrze próżnym AD jest więc tłok
drewniany EH nie dochodzący na 2 do 3 palców do wierzchu cylindra. Cylinder, postawiony spodem do
góry, wypełniony zostaje wodą, która wchodzi przez otwór wokół zatyczki
l, gdy ta jest trochę wepchnięta do środka, a przez tenże otwór wychodzi
powietrze. Po wyjściu wszystkiego powietrza, przez pociągnięcie
zatyczki zamykamy szczelnie otwór i wtedy odwracamy cylinder i
zawieszamy na haczyku naczynie, do którego możemy sypać tyle piasku lub
innego ciężaru aż się w końcu powierzchnia tłoka EF oderwie od wody.
Ponieważ trzymały się one tylko siłą oporu próżni, przeto po zważeniu
tłoka, drutu i naczynia otrzymamy wielkość tego oporu. Jeżeli na walcu
marmurowym lub szklanym zawiesimy tyle ciężaru, ile waży takiż walec
wody i dodamy jeszcze tyle, że razem z ciężarem marmuru mieć będziemy
ciężar wszystkich wymienionych obciążeń, to, gdyby wtedy nastąpiło
rozerwanie, moglibyśmy przyjąć za rzecz niewątpliwą, że próżnia stanowi
jedyną przyczynę wytrzymałości marmuru. Skoro wszakże pod tym ciężarem
ani pod cztery razy większym, nie można rozerwać marmuru, to należy
wnioskować że opór próżni wynosi tylko piątą część ogólnej
wytrzymałości, a jej reszta jest cztery razy większa od oporu próżni.
SALVIATI: Bądźcie więc dobrej myśli. Zakomunikować Wam pragnę, w
jaki sposób potęga próżni może być oddzielona od innych sił i jak ją
można zmierzyć. Dla jej wyosobnienia weźmy pod uwagę ciało, które sile
dążącej do rozerwania jego cząstek nie stawia innego oporu jak tylko
próżnię, a nasz akademik dowiódł w swoim traktacie, że takim ciałem
właśnie jest woda. Jeżeli więc tak umieścimy walec z wody, aby można
było wykazać jego wytrzymałość na rozerwanie, to ta wytrzymałość nie
będzie miała innej przyczyny, jak tylko opór stawiany przez próżnię.
Dla wykonania takiego doświadczenia obmyśliłem przyrząd, który
rysunkiem łatwiej niż słowami mogę wam przedstawić. Niech będzie CABD
(rys. 4) przekrój cylindra metalowego lub szklanego, którego
wnętrze byłoby jak najregularniej obtoczone i do tego wnętrza przylegał
ściśle wałek pełny z drzewa EFGH, mogący się posuwać w cylindrze i mający w środku otwór, przez który przechodzi zatyczka żelazna,
zakrzywiona u spodu K, a mająca na wierzchu zgrubienie ostro-kręgowe l,
zamykające ściśle lejkowaty wierzch otworu w wałku pełnym, gdy zatyczka
pociągnięta zostanie do dołu. W cylindrze próżnym AD jest więc tłok
drewniany EH nie dochodzący na 2 do 3 palców do wierzchu cylindra. Cylinder, postawiony spodem do
góry, wypełniony zostaje wodą, która wchodzi przez otwór wokół zatyczki
l, gdy ta jest trochę wepchnięta do środka, a przez tenże otwór wychodzi
powietrze. Po wyjściu wszystkiego powietrza, przez pociągnięcie
zatyczki zamykamy szczelnie otwór i wtedy odwracamy cylinder i
zawieszamy na haczyku naczynie, do którego możemy sypać tyle piasku lub
innego ciężaru aż się w końcu powierzchnia tłoka EF oderwie od wody.
Ponieważ trzymały się one tylko siłą oporu próżni, przeto po zważeniu
tłoka, drutu i naczynia otrzymamy wielkość tego oporu. Jeżeli na walcu
marmurowym lub szklanym zawiesimy tyle ciężaru, ile waży takiż walec
wody i dodamy jeszcze tyle, że razem z ciężarem marmuru mieć będziemy
ciężar wszystkich wymienionych obciążeń, to, gdyby wtedy nastąpiło
rozerwanie, moglibyśmy przyjąć za rzecz niewątpliwą, że próżnia stanowi
jedyną przyczynę wytrzymałości marmuru. Skoro wszakże pod tym ciężarem
ani pod cztery razy większym, nie można rozerwać marmuru, to należy
wnioskować że opór próżni wynosi tylko piątą część ogólnej
wytrzymałości, a jej reszta jest cztery razy większa od oporu próżni. zaliczonego przez Arystotelesa do godnych
podziwu, a dodam, należących do mechaniki; rozwiązanie to mogłoby być
nie mniej zadowalające, jak jego własne, a jednocześnie odmienne od
rozwiązania uczonego monsignora di Guevara. Najpierw wszakże trzeba
podać twierdzenie, nie tknięte przez innych, od którego zależne jest
rozwiązanie zadania i z którego, jeśli się nie mylę, dadzą się wyciągnąć
inne wiadomości nowe i godne podziwu. Dla ściślejszego zrozumienia
narysujmy figurę. (rys. 5) Niech będzie równoboczny i
równokątny wielobok, o jakiejkolwiek liczbie boków, ze środkiem w G.
Mamy więc sześciokąt ABCDEP, w który wpiszemy drugi współśrodkowy
HIKLMN. Przedłużmy bok AB większego wieloboku do S i odpowiednio bok HI
mniejszego w tym samym kierunku, tak że HT będzie równoległe do AS,
wreszcie przez środek G poprowadźmy równoległą GV. Gdy to jest zrobione,
toczmy wielobok większy, razem z małym, po linii AS. Jasne jest, że w
początku toczenia, B stoi w miejscu, A się podnosi, a C obniża
zakreślając łuk CQ, dopóki się bok BC nie położy na linii AS, jako BQ = BC. Przy tym
obrocie wszakże, wierzchołek l małego wieloboku wzniesie się ponad
linię IT, bo IB jest nachylone względem AS, a I nie wcześniej dojdzie do
równoległej IT, aż gdy C dojdzie do Q: wtedy I padnie na O, po opisaniu
łuku I0, ponad HT a IK zajmie położenie OP. Ale środek G będzie
tymczasem w ruchu ponad linią GV i nie wcześniej do niej wróci, jak po
przebieżeniu łuku GC. Po zrobieniu tego pierwszego kroku, będzie większy
wielobok leżał bokiem BC na BQ, bok małego wieloboku IK na OS, podczas
gdy cała droga I0 zostanie przeskoczona bez dotknięcia, a środek G
przejdzie do C, przebywając drogę poza równoległą GV. W końcu cała
figura zajmie położenie podobne do pierwszego, tak że przy dalszym
obrocie i drugim kroku, bok większego wieloboku DC położy się na QX,
bok małego wieloboku KL, po przekroczeniu PX na YZ, a środek G,
poruszający się wciąż ponad GV, zejdzie tam dopiero w R, po wielkim
skoku CR. W rezultacie, większy wielobok, tocząc się po AS, odetnie
sześć linii równych jego obwodowi, bez żadnych przerw; wielobok
mniejszy pokryje również sześć jednakich odcinków, równych jego
obwodowi, ale poprzegradzanych pięcioma łukami, których cięciwy nie będą
dotknięte, stanowiąc części linii HT; wreszcie środek G w sześciu
punktach tylko schodzić się będzie z równoległą GV. Pojmujecie więc. że
przestrzeń HT, przebyta przez mały wielobok, jest prawie równą AS,
przebytej przez wielobok większy, od której jest mniejsza tylko o jedną
cięciwę małego łuku, uważając linię HT razem z pięcioma łukami.
Pragnąłbym teraz, aby to, co wam przedstawiłem na przykładzie tych
sześcioboków, okazało się wam również jasne przy innych wielobokach, z
dowolną liczbą boków, a tylko do siebie podobnych, współśrodkowych i
razem ze sobą związanych, tak że przy toczeniu się większych rozważać
można toczenie się mniejszych i że drogi przebyte są prawie równe, o
ile się dolicza przestrzenie pod łukami, nie dotknięte bokami
mniejszego wieloboku. Niech więc będzie większy wielobok o 1000 boków,
które odcinamy na przebytej przezeń drodze. Równocześnie mały wielobok
przebywa prawie tę samą drogę, dotknąwszy się 1000 małych odcinków,
przegrodzonych 1000 próżni, gdyż tak je możemy nazwać w przeciwieństwie
do 1000 odcinków dotkniętych. To, co powiedziałem, nie przedstawia żadnej
trudności ani wątpliwości. Ale powiedzcie mi, jeżeli około jakiego
środka np. A, zakreślimy dwa koła współśrodkowe, związane razem i jeżeli
z końców ich średnic C i B poprowadzimy dwie styczne CE, BF, a przez
środek A równoległą AD i jeżeli toczyć będziemy koło większe po BF (i
uczynimy BF równe obwodowi koła równie jak i linie CE i AD), to po
jednym obrocie cóż się stanie z małym kołem i ze środkiem? Ten ostatni
przebiegnie niewątpliwie całą długość AD, a obwód małego koła dotknie
się swymi punktami całej linii CE, w ten sam sposób jak to było
poprzednio z wielobokiem; z tą jedyną różnicą, że tam linia HT nie we wszystkich punktach była
dotykana przez mały wielobok, bo wiele małych odcinków było
przeskoczonych, tu zaś przy kole nie może jego obwód opuszczać ani na
chwilę linii CE i każdy jego punkt musi się na niej znajdować. W jaki
więc sposób może mniejsze koło, bez przeskakiwania, przebiec drogę tak
znacznie dłuższą od swego okręgu?
zaliczonego przez Arystotelesa do godnych
podziwu, a dodam, należących do mechaniki; rozwiązanie to mogłoby być
nie mniej zadowalające, jak jego własne, a jednocześnie odmienne od
rozwiązania uczonego monsignora di Guevara. Najpierw wszakże trzeba
podać twierdzenie, nie tknięte przez innych, od którego zależne jest
rozwiązanie zadania i z którego, jeśli się nie mylę, dadzą się wyciągnąć
inne wiadomości nowe i godne podziwu. Dla ściślejszego zrozumienia
narysujmy figurę. (rys. 5) Niech będzie równoboczny i
równokątny wielobok, o jakiejkolwiek liczbie boków, ze środkiem w G.
Mamy więc sześciokąt ABCDEP, w który wpiszemy drugi współśrodkowy
HIKLMN. Przedłużmy bok AB większego wieloboku do S i odpowiednio bok HI
mniejszego w tym samym kierunku, tak że HT będzie równoległe do AS,
wreszcie przez środek G poprowadźmy równoległą GV. Gdy to jest zrobione,
toczmy wielobok większy, razem z małym, po linii AS. Jasne jest, że w
początku toczenia, B stoi w miejscu, A się podnosi, a C obniża
zakreślając łuk CQ, dopóki się bok BC nie położy na linii AS, jako BQ = BC. Przy tym
obrocie wszakże, wierzchołek l małego wieloboku wzniesie się ponad
linię IT, bo IB jest nachylone względem AS, a I nie wcześniej dojdzie do
równoległej IT, aż gdy C dojdzie do Q: wtedy I padnie na O, po opisaniu
łuku I0, ponad HT a IK zajmie położenie OP. Ale środek G będzie
tymczasem w ruchu ponad linią GV i nie wcześniej do niej wróci, jak po
przebieżeniu łuku GC. Po zrobieniu tego pierwszego kroku, będzie większy
wielobok leżał bokiem BC na BQ, bok małego wieloboku IK na OS, podczas
gdy cała droga I0 zostanie przeskoczona bez dotknięcia, a środek G
przejdzie do C, przebywając drogę poza równoległą GV. W końcu cała
figura zajmie położenie podobne do pierwszego, tak że przy dalszym
obrocie i drugim kroku, bok większego wieloboku DC położy się na QX,
bok małego wieloboku KL, po przekroczeniu PX na YZ, a środek G,
poruszający się wciąż ponad GV, zejdzie tam dopiero w R, po wielkim
skoku CR. W rezultacie, większy wielobok, tocząc się po AS, odetnie
sześć linii równych jego obwodowi, bez żadnych przerw; wielobok
mniejszy pokryje również sześć jednakich odcinków, równych jego
obwodowi, ale poprzegradzanych pięcioma łukami, których cięciwy nie będą
dotknięte, stanowiąc części linii HT; wreszcie środek G w sześciu
punktach tylko schodzić się będzie z równoległą GV. Pojmujecie więc. że
przestrzeń HT, przebyta przez mały wielobok, jest prawie równą AS,
przebytej przez wielobok większy, od której jest mniejsza tylko o jedną
cięciwę małego łuku, uważając linię HT razem z pięcioma łukami.
Pragnąłbym teraz, aby to, co wam przedstawiłem na przykładzie tych
sześcioboków, okazało się wam również jasne przy innych wielobokach, z
dowolną liczbą boków, a tylko do siebie podobnych, współśrodkowych i
razem ze sobą związanych, tak że przy toczeniu się większych rozważać
można toczenie się mniejszych i że drogi przebyte są prawie równe, o
ile się dolicza przestrzenie pod łukami, nie dotknięte bokami
mniejszego wieloboku. Niech więc będzie większy wielobok o 1000 boków,
które odcinamy na przebytej przezeń drodze. Równocześnie mały wielobok
przebywa prawie tę samą drogę, dotknąwszy się 1000 małych odcinków,
przegrodzonych 1000 próżni, gdyż tak je możemy nazwać w przeciwieństwie
do 1000 odcinków dotkniętych. To, co powiedziałem, nie przedstawia żadnej
trudności ani wątpliwości. Ale powiedzcie mi, jeżeli około jakiego
środka np. A, zakreślimy dwa koła współśrodkowe, związane razem i jeżeli
z końców ich średnic C i B poprowadzimy dwie styczne CE, BF, a przez
środek A równoległą AD i jeżeli toczyć będziemy koło większe po BF (i
uczynimy BF równe obwodowi koła równie jak i linie CE i AD), to po
jednym obrocie cóż się stanie z małym kołem i ze środkiem? Ten ostatni
przebiegnie niewątpliwie całą długość AD, a obwód małego koła dotknie
się swymi punktami całej linii CE, w ten sam sposób jak to było
poprzednio z wielobokiem; z tą jedyną różnicą, że tam linia HT nie we wszystkich punktach była
dotykana przez mały wielobok, bo wiele małych odcinków było
przeskoczonych, tu zaś przy kole nie może jego obwód opuszczać ani na
chwilę linii CE i każdy jego punkt musi się na niej znajdować. W jaki
więc sposób może mniejsze koło, bez przeskakiwania, przebiec drogę tak
znacznie dłuższą od swego okręgu? SALVIATI: Potrzeba do tego rysunku, gdyż dowód jest czysto
geometryczny. Niech będzie półkole AFB, ze środkiem w C, (rys.
6) i otaczający je prostokąt ADEB; poprowadzimy linie proste z C do
punktów D i E. Wyobraźmy sobie, że promień CF, prostopadły do AB i DE,
stoi nieruchomo, a cała figura obraca się wokół niego jako osi.
Oczywiście prostokąt ADEB opisze walec, półkole AFB - półkulę a trójkąt
CDE - ostrokrąg. Przypuśćmy następnie, że półkula zostanie wyjęta, a
pozostanie ostrokrąg i reszta cylindra, którą dla kształtu podobnego
do miski, nazwiemy poprostu miską; dowiedziemy najpierw, że miska i
ostrokrąg są równe; następnie, przeprowadziwszy płaszczyznę równoległą
do koła, będącego podstawą miski, którego średnicą jest DE a środkiem
F, dowiedziemy, że taka płaszczyzna, np. przechodząca przez GN,
przecina miskę według GION, a ostrokrąg według HL w ten sposób, że reszta
ostrokręgu CHL jest zawsze równa reszcie miski, której profil
przedstawiają trójkąty GAI, BON; okaże się dalej, że podstawa tego
ostrokręgu, tj. koło o średnicy HL, jest stale równe tej powierzchni
kołowej, która stanowi podstawę reszty miski, a którą nazwiemy wstęgą o
szerokości GI (zauważcie przy tym, jak są potrzebne określenia
matematyków, nadające nazwy albo, że tak powiem, skrócone sposoby
mówienia, zestawione i wprowadzone dla usunięcia kłopotliwego trudu,
który musielibyśmy ponosić, nie umówiwszy się nazwać np. owej
powierzchni - wstęgą kołową, a ostrego wierzchu miski - okrągłą brzytwą).
Jakkolwiek zresztą je nazwiecie, wystarczy przekonać się, że
płaszczyzna, poprowadzona w jakiejkolwiek odległości, ale równolegle do
podstawy, czyli do koła o średnicy DE, odetnie dwie bryły, zawsze równe
sobie: wierzch ostrokręgu CHL i wierzch brzytwy kołowej; a tak samo będą
sobie równe obie powierzchnie podstaw tych brył, tj. wspomniana
wstęga i koło HL. Wynika stąd zadziwiające twierdzenie, że, gdy
przypuścimy ciągłe podnoszenie się płaszczyzny przecinającej i jej
zbliżanie się do AB, to wciąż zarówno bryły odcięte, jak i powierzchnie
ich podstaw, będą sobie równe; aż w końcu tak obie bryły, jak i obie
powierzchnie zamienią się, jedne na koło a drugie na punkt, gdyż tym
jest dla jednych ostry brzeg miski, a dla drugich wierzchołek ostrokręgu.
Dalej, ponieważ przy ciągłym zmniejszaniu się obu brył utrzymuje się
stale wzajemna ich równość, przeto wnosić należy, że i ostatnie reszty
pozostaną sobie równe i nie będzie jedna nieskończenie większą od
drugiej: a więc obwód wielkiego koła może być przyrównany do jednego
punktu. A to samo, co się dzieje z bryłami, odnosi się również do ich
podstaw, które także, przy podnoszeniu się płaszczyzny przecinającej,
utrzymują wzajemną równość, aż się w końcu zamienią, równocześnie, jedna
na koło, a druga na punkt. I dlaczegóż nie mielibyśmy ich uważać za
równe, skoro są one ostatnimi resztami i śladami obu równych wielkości?
Zauważcie jeszcze, że gdyby miska była tak wielka, jak półkula nieba, to
i wtedy jej reszta byłaby równa wierzchołkowi ostrokręgu, chociaż
stanowi ją koło, będące obwodem sklepienia niebios, a wierzchołek
ostrokręgu jest tylko punktem. Na podstawie takich rozumowań twierdzimy,
że wszystkie okręgi kół, jakkolwiek są różne, mogą być nazwane równymi,
a każdy z nich równy jednemu punktowi.
SALVIATI: Potrzeba do tego rysunku, gdyż dowód jest czysto
geometryczny. Niech będzie półkole AFB, ze środkiem w C, (rys.
6) i otaczający je prostokąt ADEB; poprowadzimy linie proste z C do
punktów D i E. Wyobraźmy sobie, że promień CF, prostopadły do AB i DE,
stoi nieruchomo, a cała figura obraca się wokół niego jako osi.
Oczywiście prostokąt ADEB opisze walec, półkole AFB - półkulę a trójkąt
CDE - ostrokrąg. Przypuśćmy następnie, że półkula zostanie wyjęta, a
pozostanie ostrokrąg i reszta cylindra, którą dla kształtu podobnego
do miski, nazwiemy poprostu miską; dowiedziemy najpierw, że miska i
ostrokrąg są równe; następnie, przeprowadziwszy płaszczyznę równoległą
do koła, będącego podstawą miski, którego średnicą jest DE a środkiem
F, dowiedziemy, że taka płaszczyzna, np. przechodząca przez GN,
przecina miskę według GION, a ostrokrąg według HL w ten sposób, że reszta
ostrokręgu CHL jest zawsze równa reszcie miski, której profil
przedstawiają trójkąty GAI, BON; okaże się dalej, że podstawa tego
ostrokręgu, tj. koło o średnicy HL, jest stale równe tej powierzchni
kołowej, która stanowi podstawę reszty miski, a którą nazwiemy wstęgą o
szerokości GI (zauważcie przy tym, jak są potrzebne określenia
matematyków, nadające nazwy albo, że tak powiem, skrócone sposoby
mówienia, zestawione i wprowadzone dla usunięcia kłopotliwego trudu,
który musielibyśmy ponosić, nie umówiwszy się nazwać np. owej
powierzchni - wstęgą kołową, a ostrego wierzchu miski - okrągłą brzytwą).
Jakkolwiek zresztą je nazwiecie, wystarczy przekonać się, że
płaszczyzna, poprowadzona w jakiejkolwiek odległości, ale równolegle do
podstawy, czyli do koła o średnicy DE, odetnie dwie bryły, zawsze równe
sobie: wierzch ostrokręgu CHL i wierzch brzytwy kołowej; a tak samo będą
sobie równe obie powierzchnie podstaw tych brył, tj. wspomniana
wstęga i koło HL. Wynika stąd zadziwiające twierdzenie, że, gdy
przypuścimy ciągłe podnoszenie się płaszczyzny przecinającej i jej
zbliżanie się do AB, to wciąż zarówno bryły odcięte, jak i powierzchnie
ich podstaw, będą sobie równe; aż w końcu tak obie bryły, jak i obie
powierzchnie zamienią się, jedne na koło a drugie na punkt, gdyż tym
jest dla jednych ostry brzeg miski, a dla drugich wierzchołek ostrokręgu.
Dalej, ponieważ przy ciągłym zmniejszaniu się obu brył utrzymuje się
stale wzajemna ich równość, przeto wnosić należy, że i ostatnie reszty
pozostaną sobie równe i nie będzie jedna nieskończenie większą od
drugiej: a więc obwód wielkiego koła może być przyrównany do jednego
punktu. A to samo, co się dzieje z bryłami, odnosi się również do ich
podstaw, które także, przy podnoszeniu się płaszczyzny przecinającej,
utrzymują wzajemną równość, aż się w końcu zamienią, równocześnie, jedna
na koło, a druga na punkt. I dlaczegóż nie mielibyśmy ich uważać za
równe, skoro są one ostatnimi resztami i śladami obu równych wielkości?
Zauważcie jeszcze, że gdyby miska była tak wielka, jak półkula nieba, to
i wtedy jej reszta byłaby równa wierzchołkowi ostrokręgu, chociaż
stanowi ją koło, będące obwodem sklepienia niebios, a wierzchołek
ostrokręgu jest tylko punktem. Na podstawie takich rozumowań twierdzimy,
że wszystkie okręgi kół, jakkolwiek są różne, mogą być nazwane równymi,
a każdy z nich równy jednemu punktowi. bardzo się
mylimy, przypisując nieskończoności tż same własności co ilości
skończonej, podczas gdy te własności nie mogą się odnosić równocześnie
do obu. Dodam tu jeden zadziwiający przypadek, który przychodzi mi na
myśl, wykazujący niezmierną różnicę między tymi ilościami, oraz
sprzeciw a niemal wstręt natury do przeprowadzenia wielkości skończonej
w nieskończoną. Niech będzie jakakolwiek linia AB (rys. 7);
punkt C dzieli ją na dwie części nierówne: jeżeli z końców A i B
zataczać będziemy koła promieniami proporcjonalnymi do długości AC i
CB, to te koła przecinać się będą ze sobą w punktach leżących na
obwodzie jednego i tegoż samego koła, np. jeżeli AL : LB = AC : CB i AK
: KB = AI : IB = AC : AB itd., to punkty przecięć C L K I H G F E leżą wszystkie na
obwodzie tegoż samego koła, tak że można powiedzieć, iż skoro punkt C
tak się porusza, że jego odległości od A i B pozostają do siebie zawsze
w tym samym stosunku, to ruchem swym opisuje koło. Koło to będzie tym
większe, im punkt C jest bliższy środka O linii AB, a tym mniejsze, im C
leży bliżej B, tak że z pomiędzy nieskończenie wielu punktów, które
można wybrać między O i B, otrzymać można koła różnej wielkości, w
końcu tak małe, jak oko pchły, ale także tak wielkie, jak równik kuli
niebieskiej (del primo Mobile). Każdy punkt między O i B da koło bardzo
wielkie w pobliżu O, a zbliżając się w dalszym ciągu
do O, tak że C zejdzie się z O, jaką linię otrzymamy przy zachowaniu
pierwotnego stosunku odległości od A i B? Może okrąg koła większy od
wszelkich największych, koło nieskończonej wielkości. Ale jednocześnie
będzie to linia prosta, prostopadła do AB, przez punkt O, nieskończenie
długa i nie zakrzywiająca się na końcach, tak żeby się złączyły, jak to
miało miało miejsce z innymi liniami, bo półkole górne CHE łączyło się
z dolnym EMC. Ale przez punkt O przechodzi koło największe ze
wszystkich (gdyż wszystkie punkty z drugiej strony OA dają koła tym
większe, im bliżej leżą O), a więc nieskończenie wielkie i to koło nie
może się już zaginać i wracać do swego punktu wyjścia i
stanowi linię
prostą, jako okrąg nieskończenie wielki. Rozważcie teraz, jaka jest
różnica między kołem skończonym a nieskończenie wielkim, tak zmienia
ono swą istotę, że przestaje być kołem: dodam jeszcze, że nie może
istnieć żadne koło nieskończone, a zatem i żadna kula nieskończona, ani
jakiekolwiek nieskończone ciało lub powierzchnia. Cóż więc powiedzieć
możemy o podobnych przemianach rzeczy skończonych na nieskończone? I
dlaczego mielibyśmy się oburzać, gdyśmy przy szukaniu nieskończoności
wśród liczb znaleźli w końcu jedność? Jeżeli po rozbiciu ciała stałego
na wiele części zamienimy je na jak najdrobniejszy proszek, dochodząc do
jego nieskończenie małych składników (infiniti suoi atomi), które są już
niepodzielne, to dlaczego nie mamy powiedzieć, że ciało wróciło do
jednej ciągłości, może do stanu płynnego, jak woda, rtęć lub ten
sam metal stopiony? Czyż nie widzimy, że kamienie topią się na szkło, a
to samo szkło w silnym ogniu staje się płynniejsze od wody.
bardzo się
mylimy, przypisując nieskończoności tż same własności co ilości
skończonej, podczas gdy te własności nie mogą się odnosić równocześnie
do obu. Dodam tu jeden zadziwiający przypadek, który przychodzi mi na
myśl, wykazujący niezmierną różnicę między tymi ilościami, oraz
sprzeciw a niemal wstręt natury do przeprowadzenia wielkości skończonej
w nieskończoną. Niech będzie jakakolwiek linia AB (rys. 7);
punkt C dzieli ją na dwie części nierówne: jeżeli z końców A i B
zataczać będziemy koła promieniami proporcjonalnymi do długości AC i
CB, to te koła przecinać się będą ze sobą w punktach leżących na
obwodzie jednego i tegoż samego koła, np. jeżeli AL : LB = AC : CB i AK
: KB = AI : IB = AC : AB itd., to punkty przecięć C L K I H G F E leżą wszystkie na
obwodzie tegoż samego koła, tak że można powiedzieć, iż skoro punkt C
tak się porusza, że jego odległości od A i B pozostają do siebie zawsze
w tym samym stosunku, to ruchem swym opisuje koło. Koło to będzie tym
większe, im punkt C jest bliższy środka O linii AB, a tym mniejsze, im C
leży bliżej B, tak że z pomiędzy nieskończenie wielu punktów, które
można wybrać między O i B, otrzymać można koła różnej wielkości, w
końcu tak małe, jak oko pchły, ale także tak wielkie, jak równik kuli
niebieskiej (del primo Mobile). Każdy punkt między O i B da koło bardzo
wielkie w pobliżu O, a zbliżając się w dalszym ciągu
do O, tak że C zejdzie się z O, jaką linię otrzymamy przy zachowaniu
pierwotnego stosunku odległości od A i B? Może okrąg koła większy od
wszelkich największych, koło nieskończonej wielkości. Ale jednocześnie
będzie to linia prosta, prostopadła do AB, przez punkt O, nieskończenie
długa i nie zakrzywiająca się na końcach, tak żeby się złączyły, jak to
miało miało miejsce z innymi liniami, bo półkole górne CHE łączyło się
z dolnym EMC. Ale przez punkt O przechodzi koło największe ze
wszystkich (gdyż wszystkie punkty z drugiej strony OA dają koła tym
większe, im bliżej leżą O), a więc nieskończenie wielkie i to koło nie
może się już zaginać i wracać do swego punktu wyjścia i
stanowi linię
prostą, jako okrąg nieskończenie wielki. Rozważcie teraz, jaka jest
różnica między kołem skończonym a nieskończenie wielkim, tak zmienia
ono swą istotę, że przestaje być kołem: dodam jeszcze, że nie może
istnieć żadne koło nieskończone, a zatem i żadna kula nieskończona, ani
jakiekolwiek nieskończone ciało lub powierzchnia. Cóż więc powiedzieć
możemy o podobnych przemianach rzeczy skończonych na nieskończone? I
dlaczego mielibyśmy się oburzać, gdyśmy przy szukaniu nieskończoności
wśród liczb znaleźli w końcu jedność? Jeżeli po rozbiciu ciała stałego
na wiele części zamienimy je na jak najdrobniejszy proszek, dochodząc do
jego nieskończenie małych składników (infiniti suoi atomi), które są już
niepodzielne, to dlaczego nie mamy powiedzieć, że ciało wróciło do
jednej ciągłości, może do stanu płynnego, jak woda, rtęć lub ten
sam metal stopiony? Czyż nie widzimy, że kamienie topią się na szkło, a
to samo szkło w silnym ogniu staje się płynniejsze od wody. SALVIATI:
Niech będzie (rys. 13) AB długość drgania struny niższej, a CD
struny wyższej, która z poprzednią daje oktawę i niech będzie E środek
AB. Widać, że gdy ruch wychodzi z punktów A i C, to gdy
drganie wyższe dochodzi do D, drugie dojdzie tylko do środka E, który
nie brzmi, nie stanowiąc końca ruchu, a uderzenie będzie tylko w D. Gdy
drganie wraca od D do C, to drugie przechodzi od E do B, i wtedy dwa
uderzenia z B i C dochodzą jednocześnie do bębenka; a gdy drgania tak
następować będą po sobie, to uderzenia będą się na przemian raz spotykać,
a drugi raz nie; ale uderzeniom końcowym towarzyszyć będzie zawsze jedno
z uderzeń C, D, i zawsze to samo; wynika stąd, że gdy A i C uderzają
jednocześnie, to gdy A przechodzi do B, C idzie do D i wraca do C, tak
że pary AC są zawsze te same. Ale jeżeli drgania AB i CD dają diapentę,
to ich czasy mają się do siebie w stosunku półtoracznym i dzielić należy
AB struny niższej na trzy części równe w E i O. Drgania zaczynają się
dawać słyszeć w tej samej chwili w punktach A i C; oczywiście, gdy
uderzenie następuje w D, drganie struny niższej dochodzi do O, a
bębenek otrzymuje uderzenie tylko w D; przy powrocie od D do C, drganie
struny niższej postępuje od O do B i wraca od B do O, wykonywając
uderzenia odosobnione w B, nie wpadające w tempo uderzeń struny wyższej
(co należy zauważyć), bo ponieważ przyjęliśmy równoczesny początek drgań
w A i C, to drugie drganie, które uderzało odosobnione w D, uderzy
wracając o tyle później, ile nam trzeba na przejście od C do D lub od A
do O. Ale uderzenie w B następuje tylko o połowę tego czasu później, bo
OB=1/2 AO; dalej jedno
drganie wraca od O do A, a równocześnie drugie idzie od C do D, tak że
oba uderzają razem w A i D. Podobne okresy następują dalej, ze
wstawieniem dwóch oddzielnych i odosobnionych uderzeń wyższego tonu i
jednego odosobnionego niższego tonu, między dwa odosobnione wyższego.
Jeżeli podzielimy czas na równe małe momenty, to w pierwszych dwóch
momentach od A i od C następuje przejście do O i do D i uderzenie w D,
następnie w trzecim i czwartym momencie powrót od D do C i uderzenie w
C, a jednocześnie ruch od O do B, uderzenie w B i powrót od B do O,
wreszcie w piątym i szóstym momencie drgania od O i C do A i D i
równoczesne uderzenia w obu tych punktach, a na błonie bębenka uderzenia
następują w takim porządku, że jeżeli się spotykają na początku, to po
dwóch momentach następuje odosobnione, po trzecim znów odosobnione i tak
samo po czwartym, a po dwóch następnych dwa uderzenia razem: wtedy okres
jest ukończony i cała anomalia powtarza się wiele razy w następstwie.
SALVIATI:
Niech będzie (rys. 13) AB długość drgania struny niższej, a CD
struny wyższej, która z poprzednią daje oktawę i niech będzie E środek
AB. Widać, że gdy ruch wychodzi z punktów A i C, to gdy
drganie wyższe dochodzi do D, drugie dojdzie tylko do środka E, który
nie brzmi, nie stanowiąc końca ruchu, a uderzenie będzie tylko w D. Gdy
drganie wraca od D do C, to drugie przechodzi od E do B, i wtedy dwa
uderzenia z B i C dochodzą jednocześnie do bębenka; a gdy drgania tak
następować będą po sobie, to uderzenia będą się na przemian raz spotykać,
a drugi raz nie; ale uderzeniom końcowym towarzyszyć będzie zawsze jedno
z uderzeń C, D, i zawsze to samo; wynika stąd, że gdy A i C uderzają
jednocześnie, to gdy A przechodzi do B, C idzie do D i wraca do C, tak
że pary AC są zawsze te same. Ale jeżeli drgania AB i CD dają diapentę,
to ich czasy mają się do siebie w stosunku półtoracznym i dzielić należy
AB struny niższej na trzy części równe w E i O. Drgania zaczynają się
dawać słyszeć w tej samej chwili w punktach A i C; oczywiście, gdy
uderzenie następuje w D, drganie struny niższej dochodzi do O, a
bębenek otrzymuje uderzenie tylko w D; przy powrocie od D do C, drganie
struny niższej postępuje od O do B i wraca od B do O, wykonywając
uderzenia odosobnione w B, nie wpadające w tempo uderzeń struny wyższej
(co należy zauważyć), bo ponieważ przyjęliśmy równoczesny początek drgań
w A i C, to drugie drganie, które uderzało odosobnione w D, uderzy
wracając o tyle później, ile nam trzeba na przejście od C do D lub od A
do O. Ale uderzenie w B następuje tylko o połowę tego czasu później, bo
OB=1/2 AO; dalej jedno
drganie wraca od O do A, a równocześnie drugie idzie od C do D, tak że
oba uderzają razem w A i D. Podobne okresy następują dalej, ze
wstawieniem dwóch oddzielnych i odosobnionych uderzeń wyższego tonu i
jednego odosobnionego niższego tonu, między dwa odosobnione wyższego.
Jeżeli podzielimy czas na równe małe momenty, to w pierwszych dwóch
momentach od A i od C następuje przejście do O i do D i uderzenie w D,
następnie w trzecim i czwartym momencie powrót od D do C i uderzenie w
C, a jednocześnie ruch od O do B, uderzenie w B i powrót od B do O,
wreszcie w piątym i szóstym momencie drgania od O i C do A i D i
równoczesne uderzenia w obu tych punktach, a na błonie bębenka uderzenia
następują w takim porządku, że jeżeli się spotykają na początku, to po
dwóch momentach następuje odosobnione, po trzecim znów odosobnione i tak
samo po czwartym, a po dwóch następnych dwa uderzenia razem: wtedy okres
jest ukończony i cała anomalia powtarza się wiele razy w następstwie. Niech bowiem ciało (rys. 40) przebywa ruchem jednostajnym
z
jednakową prędkością drogi AB i BC i niech będzie DE czas potrzebny do
przebycia AB, a EF - do przebycia BC. Twierdzę, że tak się ma droga AB
do drogi BC, jak czas DE do czasu EF. Przedłużmy w obie strony linie
dróg i czasów do G, H i l, K i podzielmy AG na
dowolną liczbę dróg równych AB, i tak samo DI na takąż liczbę czasów
równych DE; z drugiej strony weźmy na CH dowolną liczbę dróg równych BC
i takąż liczbę czasów na FK równych EF. Będą więc droga BG i czas El
jednakowymi, dowolnie wybranymi, wielokrotnościami drogi BA i czasu ED, i
tak samo droga HB i czas KE takiemiż wielokrotnościami drogi CB i czasu
FE. A ponieważ DE jest czasem ruchu po AB, to czas całkowity El
odnosi się do całej drogi BG, że zaś ruch jest jednostajny, to i w
czasie El będzie tyleż części równych DE, ile jest dróg BA w całkowitej
drodze BG i tak samo znajdujemy, że KE jest czasem ruchu po HB. Wskutek zaś założenia jednostajności ruchu, gdyby GB
było równe BH, to będzie także czas IE równy czasowi EK; gdyby zaś GB
było większe lub mniejsze od BH, to także IE będzie większe lub
mniejsze od EK. Z czterech przeto rozważanych wielkości: pierwsza AB,
druga BC, trzecia DE, czwarta EF, mieszczą się pierwsza i trzecia, to
jest droga AB i czas DE, jednakową liczbę razy w drodze GB i czasie IF,
a dowiedziono, że te ostatnie są obie jednocześnie albo równe, albo
większe, albo mniejsze od czasu EK i drogi BH, a to samo odnosi się
do wielkości drugiej i czwartej. Ma się więc wielkość pierwsza do
drugiej, to jest droga AB do drogi BC, jak trzecia do czwartej, tj.
jak czas DE do czasu EF, co było do dowiedzenia.
Niech bowiem ciało (rys. 40) przebywa ruchem jednostajnym
z
jednakową prędkością drogi AB i BC i niech będzie DE czas potrzebny do
przebycia AB, a EF - do przebycia BC. Twierdzę, że tak się ma droga AB
do drogi BC, jak czas DE do czasu EF. Przedłużmy w obie strony linie
dróg i czasów do G, H i l, K i podzielmy AG na
dowolną liczbę dróg równych AB, i tak samo DI na takąż liczbę czasów
równych DE; z drugiej strony weźmy na CH dowolną liczbę dróg równych BC
i takąż liczbę czasów na FK równych EF. Będą więc droga BG i czas El
jednakowymi, dowolnie wybranymi, wielokrotnościami drogi BA i czasu ED, i
tak samo droga HB i czas KE takiemiż wielokrotnościami drogi CB i czasu
FE. A ponieważ DE jest czasem ruchu po AB, to czas całkowity El
odnosi się do całej drogi BG, że zaś ruch jest jednostajny, to i w
czasie El będzie tyleż części równych DE, ile jest dróg BA w całkowitej
drodze BG i tak samo znajdujemy, że KE jest czasem ruchu po HB. Wskutek zaś założenia jednostajności ruchu, gdyby GB
było równe BH, to będzie także czas IE równy czasowi EK; gdyby zaś GB
było większe lub mniejsze od BH, to także IE będzie większe lub
mniejsze od EK. Z czterech przeto rozważanych wielkości: pierwsza AB,
druga BC, trzecia DE, czwarta EF, mieszczą się pierwsza i trzecia, to
jest droga AB i czas DE, jednakową liczbę razy w drodze GB i czasie IF,
a dowiedziono, że te ostatnie są obie jednocześnie albo równe, albo
większe, albo mniejsze od czasu EK i drogi BH, a to samo odnosi się
do wielkości drugiej i czwartej. Ma się więc wielkość pierwsza do
drugiej, to jest droga AB do drogi BC, jak trzecia do czwartej, tj.
jak czas DE do czasu EF, co było do dowiedzenia.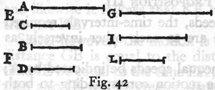 Dwa ciała (rys. 42) E i F są w ruchu jednostajnym i
stosunek prędkości ciała E do prędkości ciała F jest jak A do B; czas
zaś ruchu ciała E ma się do czasu ruchu ciała P jak C do D.
Twierdzę, że droga przebyta przez ciało E z prędkością A
w czasie C ma się do drogi przebytej przez ciało F z prędkością B
w czasie D, w stosunku złożonym ze stosunku prędkości A do prędkości B
i stosunku czasu C do czasu D. Niech będzie G droga przebyta przez
ciało E z prędkością A w czasie C i niech się ma prędkość A do prędkości
B, jak G do I, a czas C do czasu D jak l do L: wiadomo, że l jest to
droga, jaką ciało F przebywa w tym samym czasie, jak ciało E drogę G,
bo drogi G i l mają się do siebie, jak prędkości A i B: a ponieważ czas C
ma się do czasu D jak l do L, to jeżeli l jest drogą, jaką przebywa
ciało F w czasie C, będzie L drogą
przebytą przez ciało F w czasie D z prędkością B: stosunek zatem G do L
składa się ze stosunku G do I i l do L, czyli ze stosunku prędkości A do
prędkości B i czasu C do czasu D, jak to objawia podanie.
Dwa ciała (rys. 42) E i F są w ruchu jednostajnym i
stosunek prędkości ciała E do prędkości ciała F jest jak A do B; czas
zaś ruchu ciała E ma się do czasu ruchu ciała P jak C do D.
Twierdzę, że droga przebyta przez ciało E z prędkością A
w czasie C ma się do drogi przebytej przez ciało F z prędkością B
w czasie D, w stosunku złożonym ze stosunku prędkości A do prędkości B
i stosunku czasu C do czasu D. Niech będzie G droga przebyta przez
ciało E z prędkością A w czasie C i niech się ma prędkość A do prędkości
B, jak G do I, a czas C do czasu D jak l do L: wiadomo, że l jest to
droga, jaką ciało F przebywa w tym samym czasie, jak ciało E drogę G,
bo drogi G i l mają się do siebie, jak prędkości A i B: a ponieważ czas C
ma się do czasu D jak l do L, to jeżeli l jest drogą, jaką przebywa
ciało F w czasie C, będzie L drogą
przebytą przez ciało F w czasie D z prędkością B: stosunek zatem G do L
składa się ze stosunku G do I i l do L, czyli ze stosunku prędkości A do
prędkości B i czasu C do czasu D, jak to objawia podanie. SALVIATI: Rozumujecie bardzo prawdopodobnie, lecz
oprócz tego pragnę Warn przez jedno doświadczenie tak jeszcze wzmocnić
to prawdopodobieństwo, abyście je mogli przyrównać do wystarczającego
dowodzenia. Niech Wam ten papier przedstawia na poziomej płaszczyźnie
wystawioną ścianę, na wbitym w nią gwoździu wisi kula ołowiana, jedno
lub dwuuncjowa (rys. 46) zawieszona na cienkiej nici AB, dwa
do trzech łokci długiej, prostopadle do poziomu; na ścianie narysujemy
poziomą DC, przecinającą pod kątem prostym pionową AB, która na
szerokość dwóch palców jest oddalona od ściany; jeżeli nić AB z kulą
odchylimy do AC i puścimy kulę swobodnie, to zobaczymy, że ta spadając
opisze łuk CBD, przeleci przez jego spód B i biegnąc po BD podniesie się
prawie do narysowanej poziomej CD, nie dochodząc do niej tylko na
bardzo a bardzo małą odległość, wskutek oporu powietrza i nici. Stąd
możemy prawdziwie wnioskować, ze impet nabyty w punkcie B przez kulę,
przy spadaniu po łuku CB, wystarcza, aby ją podnieść po łuku BD do tej
samej wysokości; po zrobieniu i kilkakrotnym powtórzenie tego
doświadczenia, jeżeli gwóźdź wbijamy na kierunku AB w E albo w F, tak
aby sterczał na pięć lub sześć palców; to ten zatrzyma nić AC posuwającą
się przy ruchu kuli po łuku CB i wbity w E zmusi kulę do ruchu po
łuku BG, opisanym ze środka E, skąd widzimy, czego dokonać może ten sam
impet, który przedtem, poczynając od tegoż samego punktu B, podnosił
to samo ciało po łuku BD do wysokości poziomej CD. Teraz panowie
zauważcie dobrze, że kula dochodzi do linii poziomej w punkcie G i to
samo następuje, gdy przeszkodę umieścimy niżej, np. w F,
wtedy kula opisze łuk BI, kończąc zawsze swe podnoszenie się dokładnie
na linii CD; a gdyby gwóźdź przeszkadzający wbity był tak nisko, że
reszta nici nie wystarczałaby do dosięgnięcia poziomu CD (co
nastąpiłoby, gdyby gwóźdź był bliższy B niż punktu przecięcia AB z
poziomą CD), to nić nawinęłaby się na gwóźdź. Doświadczenie to nie
pozwala powątpiewać o prawdziwości przypuszczenia: bo ponieważ łuki CD i
DB są równe i podobnie położone, więc nabytek momentu przy spadaniu po
łuku CB jest ten sam, jak przy spadaniu po łuku DB; ale moment nabyty w
B, na łuku CB, wystarcza do podniesienia tegoż samego ciała po łuku BD;
więc i moment nabyty przy spadaniu po DB jest równy momentowi, który to
samo ciało podnosi po tym samym łuku od B do D, tak że w ogóle każdy
moment, osiągnięty przy spadku, jest równy temu, który może podnieść to
samo ciało po tym samym łuku: ale
wszystkie momenty, które mogą podnosić ciało po łukach BD, BG, BI, są
sobie równe, bo są nabyte przez to samo ciało przy spadaniu po łuku CB,
jak wykazało doświadczenie: a więc i wszystkie momenty, nabyte przy
spadaniu po łukach DB, GB, IB, są sobie równe.
SALVIATI: Rozumujecie bardzo prawdopodobnie, lecz
oprócz tego pragnę Warn przez jedno doświadczenie tak jeszcze wzmocnić
to prawdopodobieństwo, abyście je mogli przyrównać do wystarczającego
dowodzenia. Niech Wam ten papier przedstawia na poziomej płaszczyźnie
wystawioną ścianę, na wbitym w nią gwoździu wisi kula ołowiana, jedno
lub dwuuncjowa (rys. 46) zawieszona na cienkiej nici AB, dwa
do trzech łokci długiej, prostopadle do poziomu; na ścianie narysujemy
poziomą DC, przecinającą pod kątem prostym pionową AB, która na
szerokość dwóch palców jest oddalona od ściany; jeżeli nić AB z kulą
odchylimy do AC i puścimy kulę swobodnie, to zobaczymy, że ta spadając
opisze łuk CBD, przeleci przez jego spód B i biegnąc po BD podniesie się
prawie do narysowanej poziomej CD, nie dochodząc do niej tylko na
bardzo a bardzo małą odległość, wskutek oporu powietrza i nici. Stąd
możemy prawdziwie wnioskować, ze impet nabyty w punkcie B przez kulę,
przy spadaniu po łuku CB, wystarcza, aby ją podnieść po łuku BD do tej
samej wysokości; po zrobieniu i kilkakrotnym powtórzenie tego
doświadczenia, jeżeli gwóźdź wbijamy na kierunku AB w E albo w F, tak
aby sterczał na pięć lub sześć palców; to ten zatrzyma nić AC posuwającą
się przy ruchu kuli po łuku CB i wbity w E zmusi kulę do ruchu po
łuku BG, opisanym ze środka E, skąd widzimy, czego dokonać może ten sam
impet, który przedtem, poczynając od tegoż samego punktu B, podnosił
to samo ciało po łuku BD do wysokości poziomej CD. Teraz panowie
zauważcie dobrze, że kula dochodzi do linii poziomej w punkcie G i to
samo następuje, gdy przeszkodę umieścimy niżej, np. w F,
wtedy kula opisze łuk BI, kończąc zawsze swe podnoszenie się dokładnie
na linii CD; a gdyby gwóźdź przeszkadzający wbity był tak nisko, że
reszta nici nie wystarczałaby do dosięgnięcia poziomu CD (co
nastąpiłoby, gdyby gwóźdź był bliższy B niż punktu przecięcia AB z
poziomą CD), to nić nawinęłaby się na gwóźdź. Doświadczenie to nie
pozwala powątpiewać o prawdziwości przypuszczenia: bo ponieważ łuki CD i
DB są równe i podobnie położone, więc nabytek momentu przy spadaniu po
łuku CB jest ten sam, jak przy spadaniu po łuku DB; ale moment nabyty w
B, na łuku CB, wystarcza do podniesienia tegoż samego ciała po łuku BD;
więc i moment nabyty przy spadaniu po DB jest równy momentowi, który to
samo ciało podnosi po tym samym łuku od B do D, tak że w ogóle każdy
moment, osiągnięty przy spadku, jest równy temu, który może podnieść to
samo ciało po tym samym łuku: ale
wszystkie momenty, które mogą podnosić ciało po łukach BD, BG, BI, są
sobie równe, bo są nabyte przez to samo ciało przy spadaniu po łuku CB,
jak wykazało doświadczenie: a więc i wszystkie momenty, nabyte przy
spadaniu po łukach DB, GB, IB, są sobie równe.
 Jeżeli ciało, wychodząc ze spoczynku, spada ruchem jednostajnie
przyspieszonym, to drogi przebyte w jakichkolwiek czasach są do siebie
w podwójnym stosunku czasów, tj. w stosunku kwadratów z czasów.
Jeżeli ciało, wychodząc ze spoczynku, spada ruchem jednostajnie
przyspieszonym, to drogi przebyte w jakichkolwiek czasach są do siebie
w podwójnym stosunku czasów, tj. w stosunku kwadratów z czasów. Dla lepszego objaśnienia (rys. 51), niech będzie linia AB,
prostopadła do poziomu AC, stawiana następnie w różnych nachyleniach do
poziomu jak AD, AE, AF itd.; twierdzę, że ciało spadające po
prostopadłej BA będzie miało impet zupełny i największy, mniejszy
spadając po DA, jeszcze mniejszy po EA i wciąż zmniejszający się przy
spadaniu po FA, a w końcu zupełnie wyczerpany na poziomej CA, gdzie ciało
znajduje się w stanie obojętnym tak dla ruchu jak i dla spoczynku i samo
przez się nie ma skłonności do poruszania się w którąkolwiek stronę i
nie stawia żadnego oporu ruchowi; bo ponieważ jest niemożliwe, aby
ciało ważkie lub zespół takich ciał sam przez się podnosił się w górę,
oddalając się od wspólnego środka (commune centro), do którego dążą
wszystkie rzeczy ważkie, to niemożliwe jest także, aby się samo przez
się poruszało, jeżeli by przy takim ruchu jego własny środek ciężkości
nie zbliżał się do wzmiankowanego wspólnego środka: na poziomej więc, która tu oznacza pewną powierzchnię, wszędzie równo
oddaloną od tego środka i dlatego nie mającą żadnego nachylenia, impet
albo moment tego ciała będzie żaden. Odnośnie do tych zmian impetów,
muszę jeszcze zaznaczyć to, co w jednym dawnym traktacie mechaniki,
ułożonym kiedyś w Padwie przez naszego Akademika, wyłącznie dla użytku
jego uczniów, było wyczerpująco i gruntownie dowiedzione, przy okazji
rozważania początku i natury przedziwnego narzędzia, śruby, a
mianowicie badania, w jakim stosunku następuje zmiana impetu przy
różnych nachyleniach równi, jak np. na równi AF, której jeden koniec
jest wzniesiony na wysokość FC nad poziomem i wzdłuż tej wysokości impet
ciała ważkiego i moment spadania jest największy, szuka się tedy, w jakim
stosunku jest ten moment do momentu spadania tegoż ciała po równi FA.
Twierdzę, że ten stosunek jest odwrotnym stosunkiem tych długości i to
właśnie jest twierdzenie pomocnicze, służyć mające przy twierdzeniu,
którego mam nadzieję w następstwie móc dowieść. Jasne jest, że taki jest
impet ciała spadającego, jaki jest opór, albo najmniejsza siła,
wystarczająca do przeszkodzenia spadkowi i zatrzymania: dla zmierzenia
tej siły, czy tego oporu, użyję ciężkości innego ciała. Wyobraźmy sobie
teraz, że na równi FA leży ciało G, zaopatrzone w nitkę, która
przewinięta przez F ma przywiązany
ciężar H i weźmy pod uwagę, że droga spadania albo podnoszenia się
pionowego tego ostatniego, jest wciąż równa całkowitemu podnoszeniu się
lub spadaniu ciała G po równi pochyłej AF, ale nie już jego podnoszeniu
się lub spadaniu pionowemu, w którym to kierunku ciało G (podobnie jak
każde inne) wywiera swój opór, co jest oczywiste; bo biorąc pod uwagę
trójkąt AFC, mamy ruch ciała G np. pod górę, od A do F, złożony z
poprzecznego poziomego AC i prostopadłego CF, a że pierwszy, jak
powiedziano, nie doznaje żadnego oporu (bo przy tym ruchu nie ma żadnego
zmniejszenia lub powiększenia odległości od wspólnego środka wszystkich
ciał, gdyż ta na poziomie pozostaje zawsze ta sama), pozostaje więc
tylko opór przy podnoszeniu się wzdłuż prostopadłej CF. Skoro więc ciało
G, przy ruchu od A do F opiera się tylko podnoszeniu na wysokość CF, a
drugie ciało H w kierunku pionowym przebywa drogę równą spadkowi FA, i
ten stosunek podnoszenia się i opadania pozostaje zawsze ten sam, przy
mniejszym lub większym ruchu tych ciał (gdyż są one ze sobą związane),
możemy więc jak najpewniej twierdzić, że gdy ma nastąpić równowaga tj. stan spoczynku dla ciał, to ich momenty, prędkości, skłonności do
ruchu, tj. drogi, jakieby były przebyte przez te ciała w tym samym
czasie, są do siebie w stosunku odwrotnym do ciężkości tych ciał, co jest
dowiedzione dla wszystkich ruchów mechanicznych, tak że wystarczy do
zatrzymania spadku ciała G, aby ciało H tyle razy mniej ważyło od G, ile
wynosi stosunek FC do FA. Jeżeli więc zrobimy, że tak się ma FA do FC,
jak ciężar G do ciężaru H, to następuje równowaga, bo H i G będą miały
równe momenty i ustanie ich ruch. I skoro tylko umówimy się, że impet,
energia, moment lub skłonność ciała do ruchu tyle wynosi, co siła lub
opór najmniejszy, wystarczający do zatrzymania i gdy dowiedziono, że
ciężar H wystarcza do utrzymywania ruchu ciężaru G, to będzie mniejszy
ciężar H, działający w kierunku pionowym FC całym swym momentem, ścisłą
miarą momentu cząstkowego wywieranego przez ciężar G na równi pochyłej
FA; ale miarą całego momentu tegoż ciężaru G jest sam ten ciężar (gdyż
dla przeszkodzenia spadkowi pionowemu ciężaru użyć trzeba przeciwwagi
tak ciężkiej, jak gdyby ciężar miał swobodę ruchu pionowego); impet
zatem albo moment cząstkowy ciała G wzdłuż równi pochyłej FA, do
całkowitego albo maksymalnego impetu tegoż G na pionowej FC, stać będzie
jak ciężar H do ciężaru G, tj. na rysunku jak prostopadła FC wysokość
równi pochyłej do tejże pochyłej FA i tego mieliśmy dowieść twierdzeniem
pomocniczem, które nasz autor, jak zobaczymy, przyjmuje jako znane w
drugiej części szóstego podania niniejszej rozprawy.
Dla lepszego objaśnienia (rys. 51), niech będzie linia AB,
prostopadła do poziomu AC, stawiana następnie w różnych nachyleniach do
poziomu jak AD, AE, AF itd.; twierdzę, że ciało spadające po
prostopadłej BA będzie miało impet zupełny i największy, mniejszy
spadając po DA, jeszcze mniejszy po EA i wciąż zmniejszający się przy
spadaniu po FA, a w końcu zupełnie wyczerpany na poziomej CA, gdzie ciało
znajduje się w stanie obojętnym tak dla ruchu jak i dla spoczynku i samo
przez się nie ma skłonności do poruszania się w którąkolwiek stronę i
nie stawia żadnego oporu ruchowi; bo ponieważ jest niemożliwe, aby
ciało ważkie lub zespół takich ciał sam przez się podnosił się w górę,
oddalając się od wspólnego środka (commune centro), do którego dążą
wszystkie rzeczy ważkie, to niemożliwe jest także, aby się samo przez
się poruszało, jeżeli by przy takim ruchu jego własny środek ciężkości
nie zbliżał się do wzmiankowanego wspólnego środka: na poziomej więc, która tu oznacza pewną powierzchnię, wszędzie równo
oddaloną od tego środka i dlatego nie mającą żadnego nachylenia, impet
albo moment tego ciała będzie żaden. Odnośnie do tych zmian impetów,
muszę jeszcze zaznaczyć to, co w jednym dawnym traktacie mechaniki,
ułożonym kiedyś w Padwie przez naszego Akademika, wyłącznie dla użytku
jego uczniów, było wyczerpująco i gruntownie dowiedzione, przy okazji
rozważania początku i natury przedziwnego narzędzia, śruby, a
mianowicie badania, w jakim stosunku następuje zmiana impetu przy
różnych nachyleniach równi, jak np. na równi AF, której jeden koniec
jest wzniesiony na wysokość FC nad poziomem i wzdłuż tej wysokości impet
ciała ważkiego i moment spadania jest największy, szuka się tedy, w jakim
stosunku jest ten moment do momentu spadania tegoż ciała po równi FA.
Twierdzę, że ten stosunek jest odwrotnym stosunkiem tych długości i to
właśnie jest twierdzenie pomocnicze, służyć mające przy twierdzeniu,
którego mam nadzieję w następstwie móc dowieść. Jasne jest, że taki jest
impet ciała spadającego, jaki jest opór, albo najmniejsza siła,
wystarczająca do przeszkodzenia spadkowi i zatrzymania: dla zmierzenia
tej siły, czy tego oporu, użyję ciężkości innego ciała. Wyobraźmy sobie
teraz, że na równi FA leży ciało G, zaopatrzone w nitkę, która
przewinięta przez F ma przywiązany
ciężar H i weźmy pod uwagę, że droga spadania albo podnoszenia się
pionowego tego ostatniego, jest wciąż równa całkowitemu podnoszeniu się
lub spadaniu ciała G po równi pochyłej AF, ale nie już jego podnoszeniu
się lub spadaniu pionowemu, w którym to kierunku ciało G (podobnie jak
każde inne) wywiera swój opór, co jest oczywiste; bo biorąc pod uwagę
trójkąt AFC, mamy ruch ciała G np. pod górę, od A do F, złożony z
poprzecznego poziomego AC i prostopadłego CF, a że pierwszy, jak
powiedziano, nie doznaje żadnego oporu (bo przy tym ruchu nie ma żadnego
zmniejszenia lub powiększenia odległości od wspólnego środka wszystkich
ciał, gdyż ta na poziomie pozostaje zawsze ta sama), pozostaje więc
tylko opór przy podnoszeniu się wzdłuż prostopadłej CF. Skoro więc ciało
G, przy ruchu od A do F opiera się tylko podnoszeniu na wysokość CF, a
drugie ciało H w kierunku pionowym przebywa drogę równą spadkowi FA, i
ten stosunek podnoszenia się i opadania pozostaje zawsze ten sam, przy
mniejszym lub większym ruchu tych ciał (gdyż są one ze sobą związane),
możemy więc jak najpewniej twierdzić, że gdy ma nastąpić równowaga tj. stan spoczynku dla ciał, to ich momenty, prędkości, skłonności do
ruchu, tj. drogi, jakieby były przebyte przez te ciała w tym samym
czasie, są do siebie w stosunku odwrotnym do ciężkości tych ciał, co jest
dowiedzione dla wszystkich ruchów mechanicznych, tak że wystarczy do
zatrzymania spadku ciała G, aby ciało H tyle razy mniej ważyło od G, ile
wynosi stosunek FC do FA. Jeżeli więc zrobimy, że tak się ma FA do FC,
jak ciężar G do ciężaru H, to następuje równowaga, bo H i G będą miały
równe momenty i ustanie ich ruch. I skoro tylko umówimy się, że impet,
energia, moment lub skłonność ciała do ruchu tyle wynosi, co siła lub
opór najmniejszy, wystarczający do zatrzymania i gdy dowiedziono, że
ciężar H wystarcza do utrzymywania ruchu ciężaru G, to będzie mniejszy
ciężar H, działający w kierunku pionowym FC całym swym momentem, ścisłą
miarą momentu cząstkowego wywieranego przez ciężar G na równi pochyłej
FA; ale miarą całego momentu tegoż ciężaru G jest sam ten ciężar (gdyż
dla przeszkodzenia spadkowi pionowemu ciężaru użyć trzeba przeciwwagi
tak ciężkiej, jak gdyby ciężar miał swobodę ruchu pionowego); impet
zatem albo moment cząstkowy ciała G wzdłuż równi pochyłej FA, do
całkowitego albo maksymalnego impetu tegoż G na pionowej FC, stać będzie
jak ciężar H do ciężaru G, tj. na rysunku jak prostopadła FC wysokość
równi pochyłej do tejże pochyłej FA i tego mieliśmy dowieść twierdzeniem
pomocniczem, które nasz autor, jak zobaczymy, przyjmuje jako znane w
drugiej części szóstego podania niniejszej rozprawy. Niech będzie (rys. 52) równia pochyla AB, której
wzniesieniem nad poziom jest prostopadła AC i pozioma BC; a że
dopiero co wywiedziono, że impet ciała spadającego po prostopadłej AC ma
się do impetu tegoż po równi pochyłej AB, jak AB do AC, weźmy na równi
pochyłej AB, do AB i AC trzecią proporcjonalną AD; impet więc po AC ma
się do impetu po AB, czyli po AD, jak AC do AD, a więc ciało, w tym
samym czasie, w jakim by przebiegło drogę prostopadłą AC, przebiegnie
drogę AD po równi pochyłej AB (bo momenty mają się do siebie jak drogi),
a stopień prędkości w C do stopnia prędkości w D będzie się miał jak AC
do AD; ale stopień prędkości w B ma się do tegoż stopnia w D jak czas
spadania po AB do czasu spadania po AD, według określenia ruchu
przyspieszonego, a czas spadania po AB do czasu po AD, jak AC średnia
proporcjonalna między BA i AD do AD, zgodnie z ostatnim wnioskiem
drugiego podania, zatem stopnie prędkości w B i C mają się do stopnia w
D jak AC do AD, a więc są równe, co było twierdzeniem, jakie zamierzono
dowieść.
Niech będzie (rys. 52) równia pochyla AB, której
wzniesieniem nad poziom jest prostopadła AC i pozioma BC; a że
dopiero co wywiedziono, że impet ciała spadającego po prostopadłej AC ma
się do impetu tegoż po równi pochyłej AB, jak AB do AC, weźmy na równi
pochyłej AB, do AB i AC trzecią proporcjonalną AD; impet więc po AC ma
się do impetu po AB, czyli po AD, jak AC do AD, a więc ciało, w tym
samym czasie, w jakim by przebiegło drogę prostopadłą AC, przebiegnie
drogę AD po równi pochyłej AB (bo momenty mają się do siebie jak drogi),
a stopień prędkości w C do stopnia prędkości w D będzie się miał jak AC
do AD; ale stopień prędkości w B ma się do tegoż stopnia w D jak czas
spadania po AB do czasu spadania po AD, według określenia ruchu
przyspieszonego, a czas spadania po AB do czasu po AD, jak AC średnia
proporcjonalna między BA i AD do AD, zgodnie z ostatnim wnioskiem
drugiego podania, zatem stopnie prędkości w B i C mają się do stopnia w
D jak AC do AD, a więc są równe, co było twierdzeniem, jakie zamierzono
dowieść. Niech będzie (rys. 53) równia pochyła AC i prostopadła AB,
których wysokość jest jednakowa nad poziomem CB, jest nią mianowicie
sama linia BA: twierdzę, że czas spadku tego ciała po równi AC do czasu
spadku po prostopadłej AB, ma się tak, jak długość równi AC do długości
prostopadłej AB. Poprowadźmy jakiekolwiek linie DG, El, FL, równoległe
do poziomu CB; wiadomo z wyłożonego, że stopnie prędkości ciała,
biegnącego od pierwszego początku ruchu w A, nabyte w punktach G, D, są
równe, bo zbliżenie do poziomu jest jednakowe: podobnie takie będą
stopnie w punktach I, E, jak również w L i F. Jeżeli poprowadzimy
nie tylko te równoległe, lecz inne przechodzące przez wszystkie punkty
linii AB i ciągnące się aż do linii BC, to w punktach końcowych każdej
równoległej momenty czyli stopnie prędkości będą zawsze jednakowe. Drogi
więc AC i AB przebywane będą z tym samym stopniem prędkości. Lecz
dowiedzione było, że jeżeli dwie drogi przebywane są z tymi samymi
stopniami prędkości, to te drogi są proporcjonalne do czasów ruchu;
a więc czas spadania po AC ma się do czasu po AB, jak długość równi AC
do długości prostopadłej AB, c.b.d.d.
Niech będzie (rys. 53) równia pochyła AC i prostopadła AB,
których wysokość jest jednakowa nad poziomem CB, jest nią mianowicie
sama linia BA: twierdzę, że czas spadku tego ciała po równi AC do czasu
spadku po prostopadłej AB, ma się tak, jak długość równi AC do długości
prostopadłej AB. Poprowadźmy jakiekolwiek linie DG, El, FL, równoległe
do poziomu CB; wiadomo z wyłożonego, że stopnie prędkości ciała,
biegnącego od pierwszego początku ruchu w A, nabyte w punktach G, D, są
równe, bo zbliżenie do poziomu jest jednakowe: podobnie takie będą
stopnie w punktach I, E, jak również w L i F. Jeżeli poprowadzimy
nie tylko te równoległe, lecz inne przechodzące przez wszystkie punkty
linii AB i ciągnące się aż do linii BC, to w punktach końcowych każdej
równoległej momenty czyli stopnie prędkości będą zawsze jednakowe. Drogi
więc AC i AB przebywane będą z tym samym stopniem prędkości. Lecz
dowiedzione było, że jeżeli dwie drogi przebywane są z tymi samymi
stopniami prędkości, to te drogi są proporcjonalne do czasów ruchu;
a więc czas spadania po AC ma się do czasu po AB, jak długość równi AC
do długości prostopadłej AB, c.b.d.d. Z tego i z poprzedniego wynika, że droga, która po spadku z wyższego
punktu przebywana jest w tym samym czasie po prostopadłej i po równi
pochyłej, jest mniejszą od drogi, przebytej w tym samym czasie po równi
pochyłej, ale niepoprzedzonej spadkiem z wyższego punktu, a znów
większą od samej równi pochyłej, gdyż dowiedziono poprzednio, że w
dalszym ciągu (rys. 71) spadku z wyższego punktu A czas spadku
wzdłuż EC jest krótszy niż poprzedzający po EB, a więc droga przebywana
w czasie spadku po EB równym czasowi spadku po EC jest mniejsza od
całej drogi EB. Że zaś ta droga prostopadła jest większa od EC, to okaże
się jasne po rozpatrzeniu rysunku poprzedniego podania, gdzie
dowiedziono, że droga prostopadła BG przebyta zostaje w tym samym czasie
co i droga BC w dalszym ciągu spadku po AB: że zaś BG jest większe od
BC, tak się dowodzi. Ponieważ BE i FB są sobie równe, a BA mniejsze od
BD, przeto większy jest stosunek FB do BA aniżeli EB do BD, a stąd FA do
AB większy aniżeli ED do DB; tak się ma zatem FA do AB. jak GF do FB
(jest bowiem AF średnią proporcjonalną między BA i AG), i podobnie jak
ED do BD, tak się ma CE do EB; więc stosunek GB do BF jest większy
aniżeli CB do BE, a więc GB większe od BC.
Z tego i z poprzedniego wynika, że droga, która po spadku z wyższego
punktu przebywana jest w tym samym czasie po prostopadłej i po równi
pochyłej, jest mniejszą od drogi, przebytej w tym samym czasie po równi
pochyłej, ale niepoprzedzonej spadkiem z wyższego punktu, a znów
większą od samej równi pochyłej, gdyż dowiedziono poprzednio, że w
dalszym ciągu (rys. 71) spadku z wyższego punktu A czas spadku
wzdłuż EC jest krótszy niż poprzedzający po EB, a więc droga przebywana
w czasie spadku po EB równym czasowi spadku po EC jest mniejsza od
całej drogi EB. Że zaś ta droga prostopadła jest większa od EC, to okaże
się jasne po rozpatrzeniu rysunku poprzedniego podania, gdzie
dowiedziono, że droga prostopadła BG przebyta zostaje w tym samym czasie
co i droga BC w dalszym ciągu spadku po AB: że zaś BG jest większe od
BC, tak się dowodzi. Ponieważ BE i FB są sobie równe, a BA mniejsze od
BD, przeto większy jest stosunek FB do BA aniżeli EB do BD, a stąd FA do
AB większy aniżeli ED do DB; tak się ma zatem FA do AB. jak GF do FB
(jest bowiem AF średnią proporcjonalną między BA i AG), i podobnie jak
ED do BD, tak się ma CE do EB; więc stosunek GB do BF jest większy
aniżeli CB do BE, a więc GB większe od BC. Rozpatrując uważnie widzimy, że im mniejsza jest różnica
(rys. 81) pomiędzy linią IR a potrojonym AC, tym bardziej zbliża się równia
pochyła drugiego ruchu, to jest CO, do prostopadłej, po której w końcu
przebyta zostaje w czasie równym AC droga równa potrojonemu AC. Bo
im więcej IR zbliża się do potrojonego AC, tym bliższe będzie IM
zrównania się z MN. A ponieważ jak IM do MN na rysunku, tak będzie AC do
CE, to CE będzie mało co większym od AC i co zatem będzie punkt E bardzo
bliski punktu A, a CO i CS przecinać się będą pod bardzo ostrym kątem,
zlewając się ze sobą. Ale znów jeżeli IR będzie bardzo mało większa od
podwojonego tegoż AC, to IM będzie króciutką linią, wskutek czego AC
będzie bardzo małe w porównaniu z CE, które stanie się bardzo długie
i zbliżać się będzie do równoległej do poziomu, poprowadzonej przez C.
Wnosić stąd można, że jeżeli, jak na rysunku, w dalszym ciągu spadku po
równi pochyłej AC następuje odbicie, kierujące ciało wzdłuż linii
poziomej, jaką jest CT, to w ciągu czasu równego AC ciało przebiegnie
drogę równą zdwojonemu AC. I tu więc, jak widzimy, stosuje się podobne
rozumowanie. Wynika zaś stąd, że ponieważ tak się ma OE do OF, jak FE do
EC, to FC jest miarą czasu spadku po CO. Ale jeżeli część pozioma TC
jest równa zdwojonemu AC, to przepołówmy ją w V, a jej przedłużenie ku X
będzie nieskończenie wielkie, gdyż jej przecięcie z AE wymaga, aby
stosunek nieskończonego TX do nieskończonego VX nie był inny jak
stosunek nieskończonego VX do nieskończonego XC.
Rozpatrując uważnie widzimy, że im mniejsza jest różnica
(rys. 81) pomiędzy linią IR a potrojonym AC, tym bardziej zbliża się równia
pochyła drugiego ruchu, to jest CO, do prostopadłej, po której w końcu
przebyta zostaje w czasie równym AC droga równa potrojonemu AC. Bo
im więcej IR zbliża się do potrojonego AC, tym bliższe będzie IM
zrównania się z MN. A ponieważ jak IM do MN na rysunku, tak będzie AC do
CE, to CE będzie mało co większym od AC i co zatem będzie punkt E bardzo
bliski punktu A, a CO i CS przecinać się będą pod bardzo ostrym kątem,
zlewając się ze sobą. Ale znów jeżeli IR będzie bardzo mało większa od
podwojonego tegoż AC, to IM będzie króciutką linią, wskutek czego AC
będzie bardzo małe w porównaniu z CE, które stanie się bardzo długie
i zbliżać się będzie do równoległej do poziomu, poprowadzonej przez C.
Wnosić stąd można, że jeżeli, jak na rysunku, w dalszym ciągu spadku po
równi pochyłej AC następuje odbicie, kierujące ciało wzdłuż linii
poziomej, jaką jest CT, to w ciągu czasu równego AC ciało przebiegnie
drogę równą zdwojonemu AC. I tu więc, jak widzimy, stosuje się podobne
rozumowanie. Wynika zaś stąd, że ponieważ tak się ma OE do OF, jak FE do
EC, to FC jest miarą czasu spadku po CO. Ale jeżeli część pozioma TC
jest równa zdwojonemu AC, to przepołówmy ją w V, a jej przedłużenie ku X
będzie nieskończenie wielkie, gdyż jej przecięcie z AE wymaga, aby
stosunek nieskończonego TX do nieskończonego VX nie był inny jak
stosunek nieskończonego VX do nieskończonego XC. Przypuśćmy, że spadek się odbywa (rys. 83) po równi pochyłej
AB, po czym, wzdłuż innej równi podnoszącej się BC, następuje ruch
odbity, oraz że te równie są jednakowej długości i pod jednaowymi kątami
nachylone do poziomu GH. Wiadomo, że ciało, wychodzące ze spoczynku w A
i spadające po AB osiąga stopnie prędkości w miarę wzrostu czasu;
stopień w B, największy z osiągniętych, będzie z natury niezmiennie
pozostawał w ciele, jeżeli się nie zjawią nowe przyczyny przyspieszenia
lub opóźnienia; przyspieszenia, jeżeli ciało dalej spada, opóźnienia -
jeżeli po odbiciu podnosi się wzdłuż BC; na poziomej zaś GH ruch
ciągnąłby się do nieskończoności ze stopniem prędkości osiągniętym przez
spadek od A do B. A prędkość ta jest taka, że w ciągu czasu równego
czesowi spadku wzdłuż AB, przebyta by została wzdłuż poziomej droga
równa 2AB. Przypuśćmy teraz, że ciało porusza się z tym samym stopniem
prędkości jednostajnie wzdłuż BC, w ten sposób, że w tym samym, co
dopiero wymienionym czasie przebyta byłaby wzdłuż BC droga równa 2AB. W
rzeczywistości jednak widzimy, że ciało, zaraz gdy się zacznie podnosić,
poddane będzie tym samym wpływom, jak przy spadku wzdłuż AB, bo spadając
po BC osiągnęłoby tę samą prędkość i przebyło tę samą drogę w tym samym
czasie jak wzdłuż AB; oczywiście to zmieszanie (mixtio) ruchów,
jednostajnego pod górę, a przyspieszonego na dół, doprowadzi ciało po
równi BC do końca C, w którym osiągnięte zostaną równe stopnie
prędkości. Jeżeli weźmiemy po obu stronach punkty D, E, równo oddalone
od B, to czas spadku po DB jest równy czasowi odbicia wzdłuż BE, co tak
możemy dowieść. Poprowadzimy DF, równoległą do BC; wiadomo, że po spadku
wzdłuż AD następuje odbicie wzdłuż DF. Lecz jeżeli z D ciało biegłoby
dalej poziomo wzdłuż DE, to prędkość w E byłaby taka sama jak w D i
ciało podniosłoby się od E do C. Słusznie więc możemy twierdzić, że
jeżeli w dalszym ciągu spadku po jakiejkolwiek równi pochyłej,
następuje odbicie wzdłuż równi podnoszącej się, to ciało, wskutek
nabytego impetu wzniesie się do tej samej wysokości, czyli wzniesienia
nad poziomem. Gdy spada wzdłuż (rys. 82) AB, ciało podnosi się
wzdłuż płaszczyzny odbicia BC aż do poziomej AC; nie tylko wtedy, gdy
nachylenia równi są jednakowe, ale także gdy są nierówne, jak równia BD.
Bo na równiach o różnym nachyleniu, lecz jednakowej wysokości nabywane są
jednakowe stopnie prędkości. Jeżeli EB, BD są jednakowo nachylone, to
spadek wzdłuż ED podnosi ciało wzdłuż BD aż do D, bo taki impuls nadaje
mu impet prędkości w punkcie B; impet zaś w B jest jednakowy, czy ciało
spada wzdłuż AB, czy wzdłuż EB; wiadomo, że ciało, po swym spadku po AB
jednakowo popychane jest po BD, jak i po EB. Prawda, że czas podniesienia
po BD jest dłuższy niż po BC, jak i czas spadku po EB dłuższy niż po AB:
stosunek zaś tych czasów jest równy stosunkowi długości samych równi.
Wypada nam jeszcze znaleźć stosunek dróg przebytych wzdłuż równi różnego
nachylenia i różnej wysokości, a w równych czasach: a więc zbadać spadek
między dwiema równoległymi poziomymi. Ten zaś odbywa się według
następującego stosunku.
Przypuśćmy, że spadek się odbywa (rys. 83) po równi pochyłej
AB, po czym, wzdłuż innej równi podnoszącej się BC, następuje ruch
odbity, oraz że te równie są jednakowej długości i pod jednaowymi kątami
nachylone do poziomu GH. Wiadomo, że ciało, wychodzące ze spoczynku w A
i spadające po AB osiąga stopnie prędkości w miarę wzrostu czasu;
stopień w B, największy z osiągniętych, będzie z natury niezmiennie
pozostawał w ciele, jeżeli się nie zjawią nowe przyczyny przyspieszenia
lub opóźnienia; przyspieszenia, jeżeli ciało dalej spada, opóźnienia -
jeżeli po odbiciu podnosi się wzdłuż BC; na poziomej zaś GH ruch
ciągnąłby się do nieskończoności ze stopniem prędkości osiągniętym przez
spadek od A do B. A prędkość ta jest taka, że w ciągu czasu równego
czesowi spadku wzdłuż AB, przebyta by została wzdłuż poziomej droga
równa 2AB. Przypuśćmy teraz, że ciało porusza się z tym samym stopniem
prędkości jednostajnie wzdłuż BC, w ten sposób, że w tym samym, co
dopiero wymienionym czasie przebyta byłaby wzdłuż BC droga równa 2AB. W
rzeczywistości jednak widzimy, że ciało, zaraz gdy się zacznie podnosić,
poddane będzie tym samym wpływom, jak przy spadku wzdłuż AB, bo spadając
po BC osiągnęłoby tę samą prędkość i przebyło tę samą drogę w tym samym
czasie jak wzdłuż AB; oczywiście to zmieszanie (mixtio) ruchów,
jednostajnego pod górę, a przyspieszonego na dół, doprowadzi ciało po
równi BC do końca C, w którym osiągnięte zostaną równe stopnie
prędkości. Jeżeli weźmiemy po obu stronach punkty D, E, równo oddalone
od B, to czas spadku po DB jest równy czasowi odbicia wzdłuż BE, co tak
możemy dowieść. Poprowadzimy DF, równoległą do BC; wiadomo, że po spadku
wzdłuż AD następuje odbicie wzdłuż DF. Lecz jeżeli z D ciało biegłoby
dalej poziomo wzdłuż DE, to prędkość w E byłaby taka sama jak w D i
ciało podniosłoby się od E do C. Słusznie więc możemy twierdzić, że
jeżeli w dalszym ciągu spadku po jakiejkolwiek równi pochyłej,
następuje odbicie wzdłuż równi podnoszącej się, to ciało, wskutek
nabytego impetu wzniesie się do tej samej wysokości, czyli wzniesienia
nad poziomem. Gdy spada wzdłuż (rys. 82) AB, ciało podnosi się
wzdłuż płaszczyzny odbicia BC aż do poziomej AC; nie tylko wtedy, gdy
nachylenia równi są jednakowe, ale także gdy są nierówne, jak równia BD.
Bo na równiach o różnym nachyleniu, lecz jednakowej wysokości nabywane są
jednakowe stopnie prędkości. Jeżeli EB, BD są jednakowo nachylone, to
spadek wzdłuż ED podnosi ciało wzdłuż BD aż do D, bo taki impuls nadaje
mu impet prędkości w punkcie B; impet zaś w B jest jednakowy, czy ciało
spada wzdłuż AB, czy wzdłuż EB; wiadomo, że ciało, po swym spadku po AB
jednakowo popychane jest po BD, jak i po EB. Prawda, że czas podniesienia
po BD jest dłuższy niż po BC, jak i czas spadku po EB dłuższy niż po AB:
stosunek zaś tych czasów jest równy stosunkowi długości samych równi.
Wypada nam jeszcze znaleźć stosunek dróg przebytych wzdłuż równi różnego
nachylenia i różnej wysokości, a w równych czasach: a więc zbadać spadek
między dwiema równoległymi poziomymi. Ten zaś odbywa się według
następującego stosunku.
 Z poprzedniego wywnioskować można, że najszybszy ruch od jednego
punktu do drugiego odbywa się nie wzdłuż najkrótszej linii tj. prostej,
ale po łuku koła. Bo, dzieląc ćwierć koła (rys. 103) BAEC,
której bok BC jest prostopadły do poziomu, to jest łuk AC, na dowolną liczbę
części równych AD, DE, EF, FG, GC, prowadząc z C linie proste do punktów
A, D, E, F, G, i łącząc je liniami AD, DE, EF, VG,
GC, widzimy, że ruch wzdłuż ADC jest prędszy niż wzdłuż AC albo wzdłuż
DC po wyjściu ze spoczynku w D, ale z A będzie DC przebyte prędzej
niż obie drogi ADC, podobnie po dwóch DEC po wyjściu ze spoczynku w A
spadek odbywa się prędzej niż po samym DC. Spadek więc po trzech ADEC
będzie szybszy niż po dwóch ADC. Podobnie spadek w dalszym ciągu ADE
będzie szybszy wzdłuż dwóch EFC niż wzdłuż samego EC. Więc wzdłuż
czterech ADEFC szybszy niż wzdłuż trzech ADEC. A że wzdłuż dwóch FGC, w dalszym
ciągu spadku wzdłuż ADEF, spadek będzie szybszy niż wzdłuż FC, więc
wzdłuż pięciu ADEFGC szybszy niż wzdłuż czterech ADEFC. Im więcej
przeto wielobok wpisany zbliża się do obwodu koła, tym szybciej odbywa
się ruch między A i C.
Z poprzedniego wywnioskować można, że najszybszy ruch od jednego
punktu do drugiego odbywa się nie wzdłuż najkrótszej linii tj. prostej,
ale po łuku koła. Bo, dzieląc ćwierć koła (rys. 103) BAEC,
której bok BC jest prostopadły do poziomu, to jest łuk AC, na dowolną liczbę
części równych AD, DE, EF, FG, GC, prowadząc z C linie proste do punktów
A, D, E, F, G, i łącząc je liniami AD, DE, EF, VG,
GC, widzimy, że ruch wzdłuż ADC jest prędszy niż wzdłuż AC albo wzdłuż
DC po wyjściu ze spoczynku w D, ale z A będzie DC przebyte prędzej
niż obie drogi ADC, podobnie po dwóch DEC po wyjściu ze spoczynku w A
spadek odbywa się prędzej niż po samym DC. Spadek więc po trzech ADEC
będzie szybszy niż po dwóch ADC. Podobnie spadek w dalszym ciągu ADE
będzie szybszy wzdłuż dwóch EFC niż wzdłuż samego EC. Więc wzdłuż
czterech ADEFC szybszy niż wzdłuż trzech ADEC. A że wzdłuż dwóch FGC, w dalszym
ciągu spadku wzdłuż ADEF, spadek będzie szybszy niż wzdłuż FC, więc
wzdłuż pięciu ADEFGC szybszy niż wzdłuż czterech ADEFC. Im więcej
przeto wielobok wpisany zbliża się do obwodu koła, tym szybciej odbywa
się ruch między A i C. Niech będą (rys. 105) płaszczyzny poziome CD, BE, przecięte
prostopadłą ACB i dany stosunek drogi krótszej do dłuższej N do FG. Na
prostopadłej w górze ma być oznaczony punkt, z którego by spadające
ciało, zwrócone na CD, przebywało w czasie równym czasowi spadku drogę,
tak się mającą do drogi przebywanej przez inne ciało spadające z tegoż
samego punktu i zwrócone na płaszczyznę BE w czasie równym swemu czasowi
spadku, jak N do FG. Połóżmy GH równe N i jak FH do MG tak niech się ma
BC do CL. Twierdzę, że L będzie szukanym punktem w górze prostopadłej.
Odetnijmy CM=2CL, poprowadźmy LM, przecinającą płaszczyznę EB w O, to
będzie także BO=2BL. A ponieważ jak FH do HG, tak się ma BC do CL, to
także jak HG czyli N do GF będzie CL do LB albo CM do BO. Że zaś CM=2CL,
to CM będzie drogą, którą ciało, wyszedłszy z L, po spadku wzdłuż LC,
przebiegnie na płaszczyźnie CD; i dla tej samej przyczyny BO będzie
drogą, przebytą po spadku wzdłuż LB, w czasie równym czasowi spadku
po LB; że zaś BO jest równe 2BL, więc zadanie jest rozwiązane.
Niech będą (rys. 105) płaszczyzny poziome CD, BE, przecięte
prostopadłą ACB i dany stosunek drogi krótszej do dłuższej N do FG. Na
prostopadłej w górze ma być oznaczony punkt, z którego by spadające
ciało, zwrócone na CD, przebywało w czasie równym czasowi spadku drogę,
tak się mającą do drogi przebywanej przez inne ciało spadające z tegoż
samego punktu i zwrócone na płaszczyznę BE w czasie równym swemu czasowi
spadku, jak N do FG. Połóżmy GH równe N i jak FH do MG tak niech się ma
BC do CL. Twierdzę, że L będzie szukanym punktem w górze prostopadłej.
Odetnijmy CM=2CL, poprowadźmy LM, przecinającą płaszczyznę EB w O, to
będzie także BO=2BL. A ponieważ jak FH do HG, tak się ma BC do CL, to
także jak HG czyli N do GF będzie CL do LB albo CM do BO. Że zaś CM=2CL,
to CM będzie drogą, którą ciało, wyszedłszy z L, po spadku wzdłuż LC,
przebiegnie na płaszczyźnie CD; i dla tej samej przyczyny BO będzie
drogą, przebytą po spadku wzdłuż LB, w czasie równym czasowi spadku
po LB; że zaś BO jest równe 2BL, więc zadanie jest rozwiązane.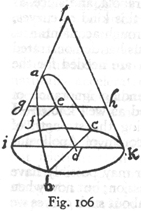 Wyobraźmy sobie (rys. 106)
stożek prosty z podstawą kołową
IBKC i wierzchołkiem w punkcie L, który przecięty płaszczyzną
równoległą do boku LK daje przecięcie BAC zwane parabolą; jej podstawa
BC przecina pod kątem prostym średnicę IK koła IBKC i niech będzie oś
paraboli AD równoległa do boku LK; weźmy jakikolwiek punkt F na linii
BFA i poprowadźmy prostą FE, równoległą do BD. Twierdzę, że kwadrat z BD
ma się do kwadratu z FE, jak oś DA do odcinka AE. Wyobraźmy sobie przez
punkt E przeprowadzoną płaszczyznę, równoległą do koła IBKC, to ta
przetnie stożek według koła o średnicy GEH. A ponieważ BD jest
prostopadła do IK, średnicy koła IBK, to kwadrat z BD jest równy
prostokątowi o bokach ID, DK. Tak samo będzie na kole górnym, przechodzącym przez punkty G, F, H, kwadrat z linii FE równy
prostokątowi o bokach GE, EH. Więc kwadraty z BD i FE mają się do siebie
jak prostokąt IDK do prostokąta GEH. A ponieważ linia ED jest
równoległa do HK, to będzie EH równe DK, gdyż są równoległe; a że
prostokąt IDK ma się do prostokąta GEH jak ID do GE, czyli jak DA do AE;
więc prostokąt IDK ma się do prostokąta GEH, jak kwadrat z BD do
kwadratu z FE, albo jak oś DA do odcinka AE, c.b.d.d.
Wyobraźmy sobie (rys. 106)
stożek prosty z podstawą kołową
IBKC i wierzchołkiem w punkcie L, który przecięty płaszczyzną
równoległą do boku LK daje przecięcie BAC zwane parabolą; jej podstawa
BC przecina pod kątem prostym średnicę IK koła IBKC i niech będzie oś
paraboli AD równoległa do boku LK; weźmy jakikolwiek punkt F na linii
BFA i poprowadźmy prostą FE, równoległą do BD. Twierdzę, że kwadrat z BD
ma się do kwadratu z FE, jak oś DA do odcinka AE. Wyobraźmy sobie przez
punkt E przeprowadzoną płaszczyznę, równoległą do koła IBKC, to ta
przetnie stożek według koła o średnicy GEH. A ponieważ BD jest
prostopadła do IK, średnicy koła IBK, to kwadrat z BD jest równy
prostokątowi o bokach ID, DK. Tak samo będzie na kole górnym, przechodzącym przez punkty G, F, H, kwadrat z linii FE równy
prostokątowi o bokach GE, EH. Więc kwadraty z BD i FE mają się do siebie
jak prostokąt IDK do prostokąta GEH. A ponieważ linia ED jest
równoległa do HK, to będzie EH równe DK, gdyż są równoległe; a że
prostokąt IDK ma się do prostokąta GEH jak ID do GE, czyli jak DA do AE;
więc prostokąt IDK ma się do prostokąta GEH, jak kwadrat z BD do
kwadratu z FE, albo jak oś DA do odcinka AE, c.b.d.d.
 Wyobraźmy sobie (rys. 108) linię albo płaszczyznę poziomą
AB, wysoko umieszczoną, po której ciało od A do B jednostajnie się
porusza; po usunięciu zagrody w B, ciało, skutkiem swej ciężkości
poddane zostaje naturalnemu spadkowi wzdłuż pionowej BN. Przedłużmy AB w
linii prostej do E i odcinajmy na BE równe części upływającego czasu
BC, CD, DE, a z punktów C, D, E, poprowadźmy równoległe do poziomej BN:
na pierwszej z nich odetnijmy jakąkolwiek długość CI, na następnej
cztery razy większą DF, potem dziewięć razy większą EH i tak dalej w
stosunku do kwadratów z CB, DB, EB, czyli w podwójnym stosunku tych
długości. Bo jeżeli przyjmujemy, że do ruchu jednostajnego od B do C,
dochodzi spadek pionowy na długości Cl, to ciało po upływie czasu BC
znajdzie się w punkcie I. Dalej w ciągu czasu DB, czyli zdwojonego BC,
będzie droga przebyta w spadku równa czterokrotnemu CI: bo w pierwszym
traktacie dowiedziono, że przy ruchu jednostajnie przyspieszonym drogi
przebyte mają się do siebie jak kwadraty z czasów. Podobnież będzie
droga EH, przebyta w spadku, w ciągu czasu BE, równa dziewięciokrotnemu
CI, bo Eli, DF, CI mają się do siebie, jak kwadraty z linij EB, DB, CB.
Jeżeli przez punkty I, F, H, poprowadzimy proste I0, FG, HL, równoległe
do EB, to będą linie HL, FG, I0 równe liniom EB, DB, CB; równie jak BO,
BG, BL są równe CI, DF, EH. Więc kwadrat z HL ma się do kwadratu FG jak
linia LB do BG; a kwadrat z FG do kwadratu z I0 jak GB do BO. Punkty
więc I, F, H, leżą na jednej i tej samej linii parabolicznej. Podobnież
biorąc inne jakiekolwiek wielkości, odpowiadające równym częściom
czasu, można by dowieść, że punkty, do których dochodzi w tych czasach
pocisk, leżą na jednej i tej samej linii parabolicznej, c.b.d.d.
Wyobraźmy sobie (rys. 108) linię albo płaszczyznę poziomą
AB, wysoko umieszczoną, po której ciało od A do B jednostajnie się
porusza; po usunięciu zagrody w B, ciało, skutkiem swej ciężkości
poddane zostaje naturalnemu spadkowi wzdłuż pionowej BN. Przedłużmy AB w
linii prostej do E i odcinajmy na BE równe części upływającego czasu
BC, CD, DE, a z punktów C, D, E, poprowadźmy równoległe do poziomej BN:
na pierwszej z nich odetnijmy jakąkolwiek długość CI, na następnej
cztery razy większą DF, potem dziewięć razy większą EH i tak dalej w
stosunku do kwadratów z CB, DB, EB, czyli w podwójnym stosunku tych
długości. Bo jeżeli przyjmujemy, że do ruchu jednostajnego od B do C,
dochodzi spadek pionowy na długości Cl, to ciało po upływie czasu BC
znajdzie się w punkcie I. Dalej w ciągu czasu DB, czyli zdwojonego BC,
będzie droga przebyta w spadku równa czterokrotnemu CI: bo w pierwszym
traktacie dowiedziono, że przy ruchu jednostajnie przyspieszonym drogi
przebyte mają się do siebie jak kwadraty z czasów. Podobnież będzie
droga EH, przebyta w spadku, w ciągu czasu BE, równa dziewięciokrotnemu
CI, bo Eli, DF, CI mają się do siebie, jak kwadraty z linij EB, DB, CB.
Jeżeli przez punkty I, F, H, poprowadzimy proste I0, FG, HL, równoległe
do EB, to będą linie HL, FG, I0 równe liniom EB, DB, CB; równie jak BO,
BG, BL są równe CI, DF, EH. Więc kwadrat z HL ma się do kwadratu FG jak
linia LB do BG; a kwadrat z FG do kwadratu z I0 jak GB do BO. Punkty
więc I, F, H, leżą na jednej i tej samej linii parabolicznej. Podobnież
biorąc inne jakiekolwiek wielkości, odpowiadające równym częściom
czasu, można by dowieść, że punkty, do których dochodzi w tych czasach
pocisk, leżą na jednej i tej samej linii parabolicznej, c.b.d.d.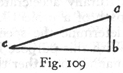 Ciało porusza się jednostajnie w dwóch kierunkach, pionowemu
odpowiada (rys. 109) droga AB; poziomemu zaś w tym samym czasie
droga BC. Ponieważ drogi AB, BC, przebywane są w tym samym czasie
ruchem jednostajnym, to momenty tych ruchów mają się do siebie jako też
same AB, BC. Ciało zaś, poruszające się według tych dwóch zmian, opisze
przekątną AC, a moment jego prędkości będzie AC. Ale AC jest
potencjalnie równe tym samym AB, BC, więc moment
złożony z dwóch momentów AB, BC jest potencjalnie równy obu razem
wziętym, c.b.d.d.
Ciało porusza się jednostajnie w dwóch kierunkach, pionowemu
odpowiada (rys. 109) droga AB; poziomemu zaś w tym samym czasie
droga BC. Ponieważ drogi AB, BC, przebywane są w tym samym czasie
ruchem jednostajnym, to momenty tych ruchów mają się do siebie jako też
same AB, BC. Ciało zaś, poruszające się według tych dwóch zmian, opisze
przekątną AC, a moment jego prędkości będzie AC. Ale AC jest
potencjalnie równe tym samym AB, BC, więc moment
złożony z dwóch momentów AB, BC jest potencjalnie równy obu razem
wziętym, c.b.d.d. Niech będzie (rys. 110) ruch po linii AB, ze spoczynku w A i
przyjmijmy na niej jakikolwiek punkt A; i połóżmy, że samo AC
przedstawia czas albo miarę czasu spadku po AC, a także miarę impetu
albo momentu nabytego w C po spadku wzdłuż AC. Weźmy dalej na tej samej
prostej AB inny punkt B, w którym impet nabyty przez ciało przy spadku
po AB oznaczony być może w stosunku do impetu nabytego w C, którego
miarą jest AC. Połóżmy AS, średnią proporcjonalną między BA i AC.
Dowiedziemy, że impet w B ma się do impetu w C, jak linia SA do AC.
Poprowadźmy poziome, CD dwa razy większą od AC i BE dwa razy większą
od BA. Wiadomo z poprzedniego, że jeżeli ciało spada po AC, a następnie
zwrócone zostanie na poziomą CD, z impetem osiągniętym w C, to
przebiegnie tam ruchem jednostajnym drogę CD w tym samym czasie, w jakim
spadało po AC; tak samo BE przebyte zostanie w tym samym czasie co AB.
Ale czas spadku po AB jest równy AS, wiec BE przebyte będzie w czasie
AS. Połóżmy teraz, że tak się ma czas SA do czasu AC, jak EB do BL. Że
zaś ruch po EB jest jednostajny, to droga BL przebyta będzie w czasie AC
z momentem prędkości w B. Ale w tym samym czasie przebyta będzie droga
CD z momentem prędkości w C: momenty zaś prędkości mają się do siebie
jak drogi z tymi momentami przebyte w tym samym czasie: zatem moment
prędkości w C ma się do momentu prędkości w B, jak DC do BL. Że zaś jak
DC do BE, tak się mają do siebie ich połowy, tj. CA do AB, a EB do BL
ma się jak BA do AS, więc CD do BL ma się jak BA do AS, więc CD do BL ma
się jak CA do AS, tj. jak moment prędkości w C do momentu prędkości w
B, tak się ma CA do AS, albo czas spadku po CA do czasu spadku po AB.
Tak się uwydatnia metoda mierzenia impetu albo momentu prędkości na
linii prostopadłego spadku, przy czym przyjęto, że impet rośnie
proporcjonalnie do czasu.
Niech będzie (rys. 110) ruch po linii AB, ze spoczynku w A i
przyjmijmy na niej jakikolwiek punkt A; i połóżmy, że samo AC
przedstawia czas albo miarę czasu spadku po AC, a także miarę impetu
albo momentu nabytego w C po spadku wzdłuż AC. Weźmy dalej na tej samej
prostej AB inny punkt B, w którym impet nabyty przez ciało przy spadku
po AB oznaczony być może w stosunku do impetu nabytego w C, którego
miarą jest AC. Połóżmy AS, średnią proporcjonalną między BA i AC.
Dowiedziemy, że impet w B ma się do impetu w C, jak linia SA do AC.
Poprowadźmy poziome, CD dwa razy większą od AC i BE dwa razy większą
od BA. Wiadomo z poprzedniego, że jeżeli ciało spada po AC, a następnie
zwrócone zostanie na poziomą CD, z impetem osiągniętym w C, to
przebiegnie tam ruchem jednostajnym drogę CD w tym samym czasie, w jakim
spadało po AC; tak samo BE przebyte zostanie w tym samym czasie co AB.
Ale czas spadku po AB jest równy AS, wiec BE przebyte będzie w czasie
AS. Połóżmy teraz, że tak się ma czas SA do czasu AC, jak EB do BL. Że
zaś ruch po EB jest jednostajny, to droga BL przebyta będzie w czasie AC
z momentem prędkości w B. Ale w tym samym czasie przebyta będzie droga
CD z momentem prędkości w C: momenty zaś prędkości mają się do siebie
jak drogi z tymi momentami przebyte w tym samym czasie: zatem moment
prędkości w C ma się do momentu prędkości w B, jak DC do BL. Że zaś jak
DC do BE, tak się mają do siebie ich połowy, tj. CA do AB, a EB do BL
ma się jak BA do AS, więc CD do BL ma się jak BA do AS, więc CD do BL ma
się jak CA do AS, tj. jak moment prędkości w C do momentu prędkości w
B, tak się ma CA do AS, albo czas spadku po CA do czasu spadku po AB.
Tak się uwydatnia metoda mierzenia impetu albo momentu prędkości na
linii prostopadłego spadku, przy czym przyjęto, że impet rośnie
proporcjonalnie do czasu. Zanim pójdziemy dalej, należy nadmienić, że ponieważ ma być mowa o
ruchu złożonym z jednostajnego poziomego i przyspieszonego z góry na
dół (bo z takiego połączenia powstaje i formuje się krążna pocisku, tj. parabola), musimy przeto ustalić pewną ogólną miarę, którą by obu
ruchów prędkości, impety lub momenty (velocitatem, impetum seu momentum) mogły być mierzone. Ze zaś
niezliczone są stopnie prędkości ruchu jednostajnego, z których nie
którykolwiek przypadkowy, lecz jeden z tych niezliczonych ma być złożony
i połączony ze stopniem prędkości, nabytym w ruchu naturalnie
przyspieszonym, to nie można obmyśleć prostszej drogi wiodącej do wyboru
i oznaczenia stopnia prędkości jak przyjęcie innego tegoż rodzaju. Aby
się zatem jaśniej wyrazić; niech będzie (rys. 111) prostopadła
AC do poziomej BC: AC będzie wysokością a CB amplitudą połowy paraboli
AB, którą opisuje złożenie dwóch ruchów, z których jeden jest spadkiem
ciała po AC, ruchem naturalnie przyspieszonym, po wyjściu ze spoczynku w
A, a drugi ruchem poprzecznym jednostajnym wzdłuż poziomej AD. Impet
nabyty w C przez spadek po AC, mierzy się tąż wysokością AC, bo zawsze
ten sam jest impet ciała spadającego z tej samej wysokości: na poziomej
zaś można dla ruchów jednostajnych wyznaczać niezliczone stopnie
prędkości; aby ten, który wybiorę z tej mnogości, oznaczyć i odróżnić od
innych, i jakby palcem go wskazać, przedłużę wysokość CA w górę i na
przedłużeniu, stosownie do potrzeby, ustalę taką wysokość AE, aby ciało,
wychodzące ze spoczynku w E i po tej wysokości spadające, osiągało w A
taki impet, z jakim ma się poruszać zwrócone na poziomą AD: jest to ten
stopień prędkości, z jakim w czasie spadku po EA, przebyta będzie
wzdłuż poziomej droga równa podwójnemu EA. Uwaga ta wydała się tu
konieczną.
Zanim pójdziemy dalej, należy nadmienić, że ponieważ ma być mowa o
ruchu złożonym z jednostajnego poziomego i przyspieszonego z góry na
dół (bo z takiego połączenia powstaje i formuje się krążna pocisku, tj. parabola), musimy przeto ustalić pewną ogólną miarę, którą by obu
ruchów prędkości, impety lub momenty (velocitatem, impetum seu momentum) mogły być mierzone. Ze zaś
niezliczone są stopnie prędkości ruchu jednostajnego, z których nie
którykolwiek przypadkowy, lecz jeden z tych niezliczonych ma być złożony
i połączony ze stopniem prędkości, nabytym w ruchu naturalnie
przyspieszonym, to nie można obmyśleć prostszej drogi wiodącej do wyboru
i oznaczenia stopnia prędkości jak przyjęcie innego tegoż rodzaju. Aby
się zatem jaśniej wyrazić; niech będzie (rys. 111) prostopadła
AC do poziomej BC: AC będzie wysokością a CB amplitudą połowy paraboli
AB, którą opisuje złożenie dwóch ruchów, z których jeden jest spadkiem
ciała po AC, ruchem naturalnie przyspieszonym, po wyjściu ze spoczynku w
A, a drugi ruchem poprzecznym jednostajnym wzdłuż poziomej AD. Impet
nabyty w C przez spadek po AC, mierzy się tąż wysokością AC, bo zawsze
ten sam jest impet ciała spadającego z tej samej wysokości: na poziomej
zaś można dla ruchów jednostajnych wyznaczać niezliczone stopnie
prędkości; aby ten, który wybiorę z tej mnogości, oznaczyć i odróżnić od
innych, i jakby palcem go wskazać, przedłużę wysokość CA w górę i na
przedłużeniu, stosownie do potrzeby, ustalę taką wysokość AE, aby ciało,
wychodzące ze spoczynku w E i po tej wysokości spadające, osiągało w A
taki impet, z jakim ma się poruszać zwrócone na poziomą AD: jest to ten
stopień prędkości, z jakim w czasie spadku po EA, przebyta będzie
wzdłuż poziomej droga równa podwójnemu EA. Uwaga ta wydała się tu
konieczną. Niech będzie (rys. 112) połowa paraboli BEC, jej amplituda
CD, wysokość DB, która w górę przedłużona spotyka w A styczną CA do
paraboli, a przez wierzchołek B poprowadzona równoległa BI do poziomu
CD. Jeżeli amplituda CD jest równa całej wysokości DA, to będzie BI
równe BA i równe BD. A jeżeli przyjmiemy, że AB jest miarą czasu spadku
po AB i miarą momentu prędkości nabytego w B przy spadku wzdłuż AB po
wyjściu ze spoczynku w A, to DC
(podwojone BI) będzie drogą, która z impetem
osiągniętym wzdłuż AB, po skierowaniu ciała na poziomą przebyta
zostanie w tym samym czasie. Lecz w ciągu tegoż czasu, ciało spadające
po BD ze spoczynku w B, przebywa wysokość BD, więc spadające po AB ze
spoczynku w A, zwrócone z impetem AB na poziomą, przebiegnie drogę
równą DC. Przyłączający się spadek po BD przebywa wysokość BD; i
opisana zostaje parabola BC: na której impet w końcu C składa się z
jednostajnego poprzecznego; którego moment jest AB i z drugiego momentu
nabytego przy spadku BD w końcu D czyli C; które to oba momenty są
sobie równe. Jeżeli więc AB jest miarą jednego z nich, mianowicie
jednostajnego poprzecznego, to BI równe BD będzie miarą impetu
osiągniętego w D lub C, a prosta IA będzie ilością momentu złożonego z
obu: będzie więc ona także ilością czyli miarą całego momentu, jaki
pocisk biegnący po paraboli BC posiada jako impet w C. To założywszy,
weźmy na paraboli jakikolwiek punkt E, w którym oznaczony ma być impet
pocisku. Poprowadźmy poziomą EF i weźmy BG średnią proporcjonalną
między BD i BF. Ponieważ AB, czyli BD, jest miarą czasu i momentu
prędkości (momentum velocitatis) przy spadku BD ze spoczynku w B, to BG będzie czasem, albo
miarą czasu impetu w F przy zejściu z B. Jeżeli zatem położymy BO równe
BG, to łącząca przekątna AO będzie ilością impetu w punkcie E; albowiem
AB przyjęto jako miarę czasu i impetu w B, który po skierowaniu ciała na
poziomą dalej się utrzymuje; BO zaś określa impet w F, albo w E, przy
spadku ze spoczynku w B wzdłuż wysokości BF, te zaś AB, BO, równoważone
są potencjalnie przez AO, otrzymuje się więc co było żądane.
Niech będzie (rys. 112) połowa paraboli BEC, jej amplituda
CD, wysokość DB, która w górę przedłużona spotyka w A styczną CA do
paraboli, a przez wierzchołek B poprowadzona równoległa BI do poziomu
CD. Jeżeli amplituda CD jest równa całej wysokości DA, to będzie BI
równe BA i równe BD. A jeżeli przyjmiemy, że AB jest miarą czasu spadku
po AB i miarą momentu prędkości nabytego w B przy spadku wzdłuż AB po
wyjściu ze spoczynku w A, to DC
(podwojone BI) będzie drogą, która z impetem
osiągniętym wzdłuż AB, po skierowaniu ciała na poziomą przebyta
zostanie w tym samym czasie. Lecz w ciągu tegoż czasu, ciało spadające
po BD ze spoczynku w B, przebywa wysokość BD, więc spadające po AB ze
spoczynku w A, zwrócone z impetem AB na poziomą, przebiegnie drogę
równą DC. Przyłączający się spadek po BD przebywa wysokość BD; i
opisana zostaje parabola BC: na której impet w końcu C składa się z
jednostajnego poprzecznego; którego moment jest AB i z drugiego momentu
nabytego przy spadku BD w końcu D czyli C; które to oba momenty są
sobie równe. Jeżeli więc AB jest miarą jednego z nich, mianowicie
jednostajnego poprzecznego, to BI równe BD będzie miarą impetu
osiągniętego w D lub C, a prosta IA będzie ilością momentu złożonego z
obu: będzie więc ona także ilością czyli miarą całego momentu, jaki
pocisk biegnący po paraboli BC posiada jako impet w C. To założywszy,
weźmy na paraboli jakikolwiek punkt E, w którym oznaczony ma być impet
pocisku. Poprowadźmy poziomą EF i weźmy BG średnią proporcjonalną
między BD i BF. Ponieważ AB, czyli BD, jest miarą czasu i momentu
prędkości (momentum velocitatis) przy spadku BD ze spoczynku w B, to BG będzie czasem, albo
miarą czasu impetu w F przy zejściu z B. Jeżeli zatem położymy BO równe
BG, to łącząca przekątna AO będzie ilością impetu w punkcie E; albowiem
AB przyjęto jako miarę czasu i impetu w B, który po skierowaniu ciała na
poziomą dalej się utrzymuje; BO zaś określa impet w F, albo w E, przy
spadku ze spoczynku w B wzdłuż wysokości BF, te zaś AB, BO, równoważone
są potencjalnie przez AO, otrzymuje się więc co było żądane. prostopadłej AB (rys. 114) ma np.
3 stopnie impetu równomiernego, ale przenoszone jest przez AB ku C z
prędkością i impetem 4 stopni, tak, że w tym samym czasie, gdy
spadając przebiegnie po prostopadłej 3 łokcie, to po poziomej
przejdzie 4; lecz przez złożenie obu prędkości przejdzie ono w ciągu
tego czasu od A do C, postępując ciągle po przekątnej AC, której długość
nie wynosi 7, to jest sumy z AB, 3 i BC, 4, ale 5, które potencjalnie
jest równe obu 3 i 4. Bo jeżeli weźmiemy kwadraty z 3 i 4, to jest 9 i
18 i połączymy je, to utworzą razem 25, jako kwadrat z AC, równy obu
kwadratom z AB i BC, a więc AC będzie bokiem, a raczej pierwiastkiem
kwadratu 25, czyli będzie 5. Przyjąć więc należy, za prawidło ścisłe i
pewne, że gdy chodzi o oznaczenie ilości impetu, złożonego z dwóch
impetów danych, jednego poziomego, drugiego prostopadłego a obu
jednostajnych, należy utworzyć z nich kwadraty i dodać do siebie,
następnie wyciągnąć pierwiastek z sumy, który da ilość impetu złożonego
z obu. I jak w naszym przykładzie ciało wskutek ruchu prostopadłego
miałoby popchnięcie do poziomu z siłą 3 stopni, a w ruchu poziomym
uderzenie w C z 4 stopniami, popychane przez oba połączone impety,
będzie ono jakby uderzone i poruszające się z 5 stopniami prędkości i
siły. A uderzenie to mieć będzie tę samą wartość we wszystkich
punktach przekątnej AC, dopókąd impety składowe pozostają te same, nie
rosną i nie zmniejszają się.
prostopadłej AB (rys. 114) ma np.
3 stopnie impetu równomiernego, ale przenoszone jest przez AB ku C z
prędkością i impetem 4 stopni, tak, że w tym samym czasie, gdy
spadając przebiegnie po prostopadłej 3 łokcie, to po poziomej
przejdzie 4; lecz przez złożenie obu prędkości przejdzie ono w ciągu
tego czasu od A do C, postępując ciągle po przekątnej AC, której długość
nie wynosi 7, to jest sumy z AB, 3 i BC, 4, ale 5, które potencjalnie
jest równe obu 3 i 4. Bo jeżeli weźmiemy kwadraty z 3 i 4, to jest 9 i
18 i połączymy je, to utworzą razem 25, jako kwadrat z AC, równy obu
kwadratom z AB i BC, a więc AC będzie bokiem, a raczej pierwiastkiem
kwadratu 25, czyli będzie 5. Przyjąć więc należy, za prawidło ścisłe i
pewne, że gdy chodzi o oznaczenie ilości impetu, złożonego z dwóch
impetów danych, jednego poziomego, drugiego prostopadłego a obu
jednostajnych, należy utworzyć z nich kwadraty i dodać do siebie,
następnie wyciągnąć pierwiastek z sumy, który da ilość impetu złożonego
z obu. I jak w naszym przykładzie ciało wskutek ruchu prostopadłego
miałoby popchnięcie do poziomu z siłą 3 stopni, a w ruchu poziomym
uderzenie w C z 4 stopniami, popychane przez oba połączone impety,
będzie ono jakby uderzone i poruszające się z 5 stopniami prędkości i
siły. A uderzenie to mieć będzie tę samą wartość we wszystkich
punktach przekątnej AC, dopókąd impety składowe pozostają te same, nie
rosną i nie zmniejszają się. potencjalnie równy obu składowym. Ale lepiej jeszcze objaśnię to na przykładzie.
Niech będzie (rys. 115) na prostopadłej do poziomu AC wzięta jakakolwiek część AB,
która jednocześnie mierzy drogę ruchu naturalnego po tej prostopadłej,
a także jest miarą czasu i stopnia prędkości a raczej impetu.
Oczywistem jest najpierw, że impet ciała spadającego z A przemieni się w
B na ruch jednostajnie wzdłuż BD równoległej do poziomu, a ilość
prędkości tego ruchu będzie taka, że w ciągu czasu AB ciało przebiegnie
podwójną drogę AB i tak długą niech będzie BD. Połóżmy dalej BC=BA,
poprowadźmy CE równoległą do BD i jej równą, i opiszmy przez punkty B,
E, linią paraboliczną BEI. A ponieważ w ciągu czasu AB z impetem AB
przebywana jest pozioma BD lub CE, dwa razy większa od AB i w tym
samym czasie prostopadła BC z impetem nabytym w C, równym poziomemu,
więc ciało po upływie czasu AB znajdzie się w B, przebywszy od E
parabolę BE, i mieć będzie impet złożony z dwóch, z których każdy jest
równy impetowi AB. A ponieważ jeden z nich jest poziomy, a drugi
pionowy, to impet wypadkowy będzie potencjalnie równy obu składowym.
Połóżmy więc BF=BA i poprowadźmy przekątną AF; impet i uderzenie w E
będzie większe od uderzenia w B, ciała spadającego z wysokości A, albo
od uderzenia impetu poziomego wzdłuż BD, w stosunku AF do AB. Ale jeżeli
uważamy zawsze BA za miarę drogi spadku od spoczynku w A do B, oraz
miarę czasu i impetu, jaki ciało spadające nabywa w B, to wysokość BO
nie byłaby równą ale większą od AB; wziąwszy BG średnią proporcjonalną
między AB i BO, będzie BG miarą czasu i impetu w O, nabytego przy spadku
z wysokości BO; droga po poziomej, która przebyła z impetem AB w ciągu
czasu AB była dwa razy większa od AB, będzie w ciągu czasu BG o tyle
większa, o ile BG jest większe od BA. Połóżmy LB=BG i poprowadźmy
przekątną AL, a otrzymamy ilość złożoną z dwóch impetów, poziomego i
pionowego, które opisują parabolę: z nich poziomy jest jednostajny,
nabyty w B przez spadek po AB, a drugi jest nabyty w O, a raczej w I,
przez spadek po BO w ciągu czasu BG, które jest zarazem ilością jego
momentu. Podobnie znajdziemy impet w końcowym punkcie paraboli, gdy jej
wysokość będzie mniejsza od wyniosłości AB, biorąc między obiema
średnią proporcjonalną; ta, umieszczona na poziomej zamiast BF, pozwala
poprowadzić przekątną jak AF będącą ilością impetu w punkcie końcowym
paraboli.
potencjalnie równy obu składowym. Ale lepiej jeszcze objaśnię to na przykładzie.
Niech będzie (rys. 115) na prostopadłej do poziomu AC wzięta jakakolwiek część AB,
która jednocześnie mierzy drogę ruchu naturalnego po tej prostopadłej,
a także jest miarą czasu i stopnia prędkości a raczej impetu.
Oczywistem jest najpierw, że impet ciała spadającego z A przemieni się w
B na ruch jednostajnie wzdłuż BD równoległej do poziomu, a ilość
prędkości tego ruchu będzie taka, że w ciągu czasu AB ciało przebiegnie
podwójną drogę AB i tak długą niech będzie BD. Połóżmy dalej BC=BA,
poprowadźmy CE równoległą do BD i jej równą, i opiszmy przez punkty B,
E, linią paraboliczną BEI. A ponieważ w ciągu czasu AB z impetem AB
przebywana jest pozioma BD lub CE, dwa razy większa od AB i w tym
samym czasie prostopadła BC z impetem nabytym w C, równym poziomemu,
więc ciało po upływie czasu AB znajdzie się w B, przebywszy od E
parabolę BE, i mieć będzie impet złożony z dwóch, z których każdy jest
równy impetowi AB. A ponieważ jeden z nich jest poziomy, a drugi
pionowy, to impet wypadkowy będzie potencjalnie równy obu składowym.
Połóżmy więc BF=BA i poprowadźmy przekątną AF; impet i uderzenie w E
będzie większe od uderzenia w B, ciała spadającego z wysokości A, albo
od uderzenia impetu poziomego wzdłuż BD, w stosunku AF do AB. Ale jeżeli
uważamy zawsze BA za miarę drogi spadku od spoczynku w A do B, oraz
miarę czasu i impetu, jaki ciało spadające nabywa w B, to wysokość BO
nie byłaby równą ale większą od AB; wziąwszy BG średnią proporcjonalną
między AB i BO, będzie BG miarą czasu i impetu w O, nabytego przy spadku
z wysokości BO; droga po poziomej, która przebyła z impetem AB w ciągu
czasu AB była dwa razy większa od AB, będzie w ciągu czasu BG o tyle
większa, o ile BG jest większe od BA. Połóżmy LB=BG i poprowadźmy
przekątną AL, a otrzymamy ilość złożoną z dwóch impetów, poziomego i
pionowego, które opisują parabolę: z nich poziomy jest jednostajny,
nabyty w B przez spadek po AB, a drugi jest nabyty w O, a raczej w I,
przez spadek po BO w ciągu czasu BG, które jest zarazem ilością jego
momentu. Podobnie znajdziemy impet w końcowym punkcie paraboli, gdy jej
wysokość będzie mniejsza od wyniosłości AB, biorąc między obiema
średnią proporcjonalną; ta, umieszczona na poziomej zamiast BF, pozwala
poprowadzić przekątną jak AF będącą ilością impetu w punkcie końcowym
paraboli. Niech będzie (rys. 116) parabola AB, jej amplituda HB,
przedłużenie jej osi HE, na którym ma być oznaczona wyniosłość, z
której spadające ciało, z impetem osiągniętym w A zwrócone na poziomą,
opisuje parabolę AB. Poprowadźmy poziomą AG, równoległą do BH i połóżmy
AF=AH, poprowadźmy prostą FB, styczną do paraboli w B, a przecinającą w
G poziomą AG; odetnijmy AE trzecią proporcjonalną
do FA i AG. Twierdzę, że E będzie szukanym punktem, z którego ciało,
wychodzące ze spoczynku w E i z nabytym impetem w A skierowane poziomo
razem z impetem spadku ze spoczynku w A do H, opisze parabolę AB. Bo
jeżeli EA jest czasem spadku od E do A a jednocześnie miarą impetu
nabytego w A, to będzie AG (średnia proporcjonalna między EA i AF)
czasem spadku i impetu przy spadku z F do A, albo z A do H. A ponieważ
ciało spadające z E, z impetem nabytym w A, przebędzie ruchem
jednostajnym na poziomie drogę równą podwojonemu EA, a w czasie i z
impetem AG drogę równą podwojonemu GA czyli BH (bo przy ruchu
jednostajnym drogi są proporcjonalne do czasów), a w ruchu prostopadłym
ze spoczynku w czasie GA przebiegnie drogę AH; zatem w tym
samym czasie przebyta będzie przez ciało amplituda HB i wysokość AH.
Ciało więc spadające z E opisze parabolę AB, jak to było założone.
Niech będzie (rys. 116) parabola AB, jej amplituda HB,
przedłużenie jej osi HE, na którym ma być oznaczona wyniosłość, z
której spadające ciało, z impetem osiągniętym w A zwrócone na poziomą,
opisuje parabolę AB. Poprowadźmy poziomą AG, równoległą do BH i połóżmy
AF=AH, poprowadźmy prostą FB, styczną do paraboli w B, a przecinającą w
G poziomą AG; odetnijmy AE trzecią proporcjonalną
do FA i AG. Twierdzę, że E będzie szukanym punktem, z którego ciało,
wychodzące ze spoczynku w E i z nabytym impetem w A skierowane poziomo
razem z impetem spadku ze spoczynku w A do H, opisze parabolę AB. Bo
jeżeli EA jest czasem spadku od E do A a jednocześnie miarą impetu
nabytego w A, to będzie AG (średnia proporcjonalna między EA i AF)
czasem spadku i impetu przy spadku z F do A, albo z A do H. A ponieważ
ciało spadające z E, z impetem nabytym w A, przebędzie ruchem
jednostajnym na poziomie drogę równą podwojonemu EA, a w czasie i z
impetem AG drogę równą podwojonemu GA czyli BH (bo przy ruchu
jednostajnym drogi są proporcjonalne do czasów), a w ruchu prostopadłym
ze spoczynku w czasie GA przebiegnie drogę AH; zatem w tym
samym czasie przebyta będzie przez ciało amplituda HB i wysokość AH.
Ciało więc spadające z E opisze parabolę AB, jak to było założone. Niech będzie AC (rys. 117), prostopadła do poziomej DC, na
której dana jest wysokość CB i wyniosłość BA. Oznaczyć trzeba na
poziomej CD amplitudę tej półparaboli, którą ciało z wyniosłości BA
opisze z wysokością BC. Weźmy średnią proporcjonalną między CB i BA i
odetnijmy CD równą tejże podwojonej. Twierdzę, że CD będzie szukaną
amplitudą. Wynika to z poprzedniego.
Niech będzie AC (rys. 117), prostopadła do poziomej DC, na
której dana jest wysokość CB i wyniosłość BA. Oznaczyć trzeba na
poziomej CD amplitudę tej półparaboli, którą ciało z wyniosłości BA
opisze z wysokością BC. Weźmy średnią proporcjonalną między CB i BA i
odetnijmy CD równą tejże podwojonej. Twierdzę, że CD będzie szukaną
amplitudą. Wynika to z poprzedniego. poziomą BE przecinającą w E, będzie więc BE równe BC albo równe BA;
wiadomo, że parabolę opisuje ciało, którego impet jednostajny poziomy
jest taki jak nabyty w B przy spadku ze spoczynku w A, a impet naturalny
z góry na dół, jak w C przy spadku ze spoczynku w B. Wynika stąd, że
impet z tych dwóch złożony, działający w punkcie końcowym D będzie jak
przekątna AE równy potencjalnie obu. Niech będzie GD jakakolwiek inna
półparabola z tą samą amplitudą CD, lecz z wysokością CG, mniejszą lub
większą od wysokości BC; styczną do niej będzie HD, przecinająca poziomą
przeprowadzoną przez G w punkcie K; i niech będzie jak HG do GK, tak
KG do GL, z której to wysokości GL, wedle tego co poprzednio
dowiedziono, spadające ciało opisuje parabolę GD. Między AB i GL niech
będzie średnia proporcjonalna GM: to GM będzie czasem i momentem albo
impetem w G przy spadku z L (założono bowiem, że AB jest miarą czasu i
impetu). Niech będzie znów, między HC i CG średnia proporcjonalna GN,
będzie ona miarą czasu i impetu przy spadku z G do C. Jeżeli
poprowadzimy MN, to będzie ono miarą impetu ciała opisującego parabolę
BD, osiągniętego w punkcie końcowym D. Twierdzę, że impet ten jest
większy od impetu na paraboli BD, który się równał AE. Albowiem GN jest
średnią między BC i CG, a że BC równe BE, to jest równe GK (bo obie są
połową DC); będzie więc jak CG do GN, tak NG do GK i jak CG albo HG do
GK, tak kwadrat z NG do kwadratu z GK; jak zatem HG do GK, tak się ma KG
do GL a więc jak kwadrat z NG do kwadratu z GK, tak się ma KG do GL;
lecz jak KG do GL, tak się ma kwadrat z KG do kwadratu z GM (bo GM jest
średnią między KG i GL), a więc trzy kwadraty NG, GK i GM tworzą ciąg
proporcjonalny, a dwa skrajne NG i GM razem
wzięte dają kwadrat z NM większy od podwojonego kwadratu z KG, który
jest równy podwojonemu kwadratowi z AE: więc kwadrat z MN jest większy
od kwadratu z AE i linia NM większa od linii EA, c.b.d.d.
poziomą BE przecinającą w E, będzie więc BE równe BC albo równe BA;
wiadomo, że parabolę opisuje ciało, którego impet jednostajny poziomy
jest taki jak nabyty w B przy spadku ze spoczynku w A, a impet naturalny
z góry na dół, jak w C przy spadku ze spoczynku w B. Wynika stąd, że
impet z tych dwóch złożony, działający w punkcie końcowym D będzie jak
przekątna AE równy potencjalnie obu. Niech będzie GD jakakolwiek inna
półparabola z tą samą amplitudą CD, lecz z wysokością CG, mniejszą lub
większą od wysokości BC; styczną do niej będzie HD, przecinająca poziomą
przeprowadzoną przez G w punkcie K; i niech będzie jak HG do GK, tak
KG do GL, z której to wysokości GL, wedle tego co poprzednio
dowiedziono, spadające ciało opisuje parabolę GD. Między AB i GL niech
będzie średnia proporcjonalna GM: to GM będzie czasem i momentem albo
impetem w G przy spadku z L (założono bowiem, że AB jest miarą czasu i
impetu). Niech będzie znów, między HC i CG średnia proporcjonalna GN,
będzie ona miarą czasu i impetu przy spadku z G do C. Jeżeli
poprowadzimy MN, to będzie ono miarą impetu ciała opisującego parabolę
BD, osiągniętego w punkcie końcowym D. Twierdzę, że impet ten jest
większy od impetu na paraboli BD, który się równał AE. Albowiem GN jest
średnią między BC i CG, a że BC równe BE, to jest równe GK (bo obie są
połową DC); będzie więc jak CG do GN, tak NG do GK i jak CG albo HG do
GK, tak kwadrat z NG do kwadratu z GK; jak zatem HG do GK, tak się ma KG
do GL a więc jak kwadrat z NG do kwadratu z GK, tak się ma KG do GL;
lecz jak KG do GL, tak się ma kwadrat z KG do kwadratu z GM (bo GM jest
średnią między KG i GL), a więc trzy kwadraty NG, GK i GM tworzą ciąg
proporcjonalny, a dwa skrajne NG i GM razem
wzięte dają kwadrat z NM większy od podwojonego kwadratu z KG, który
jest równy podwojonemu kwadratowi z AE: więc kwadrat z MN jest większy
od kwadratu z AE i linia NM większa od linii EA, c.b.d.d. W trójkącie prostokątnym (rys. 119) MCB niech będzie pozioma
BC równa pionowej CM, tak, że kąt MBC jest połową prostego: przedłużmy
CM do D i wykreślmy nad i pod przekątną MB przy wierzchołku B dwa równe
kąty MBE i MBD. Dowieść mamy, że amplitudy parabol opisanych przez
pociski wyrzucone z B z jednakowym impetem, przy nachyleniach EBC i DBC
są sobie równe. Ponieważ bowiem kąt zewnętrzny BMC jest równy
wewnętrznym MDB, DBM, więc tym obu równy jest także kąt MBC. Jeżeli
zamiast kąta DBM weźmiemy kąt MBE, to będzie MBC równy dwu MBE, BDC, a
po odjęciu wspólnego MBE zostanie reszta BDC równa reszcie EBC.
Trójkąty zatem DCB i BCE są podobne. Przepołówmy proste DC i EC w H i F,
poprowadźmy HI, FG równoległe do poziomej CB i jak DH do HI, niech
będzie IH do HL; będzie zatem trójkąt IHL podobny IHD, któremu znów jest
podobny EGF, że zaś IH, GF są równe (bo każda jest połową BC), więc FE,
czyli FC jest równe HL, a dodając do obu FH, otrzymamy CH równe FL.
Jeżeli teraz wyobrazimy sobie połowę paraboli, przechodzącą przez H i
B, o wysokości HC, a wyniosłości HL, to jej amplituda będzie CB, które
jest równe podwojonemu HI, podczas gdy HI jest średnią proporcjonalną
między DH albo CH i HL; styczną więc do niej będzie DB wobec równości
CH i HD. Jeżeli znów wyobrazimy sobie parabolę, przechodzącą przez F i
B, z wyniosłością FL a wysokością FC, między którymi średnią
proporcjonalną jest FG, równe połowie poziomej CB, to tak samo
amplitudą jej będzie CB: styczną zaś do niej jest EB, bo EF i FC są
sobie równe. Ze zaś kąty DBC, EBC (nachylenia rzutu) różnią się
jednakowo od połowy kąta prostego, przeto twierdzenie jest
dowiedzione.
W trójkącie prostokątnym (rys. 119) MCB niech będzie pozioma
BC równa pionowej CM, tak, że kąt MBC jest połową prostego: przedłużmy
CM do D i wykreślmy nad i pod przekątną MB przy wierzchołku B dwa równe
kąty MBE i MBD. Dowieść mamy, że amplitudy parabol opisanych przez
pociski wyrzucone z B z jednakowym impetem, przy nachyleniach EBC i DBC
są sobie równe. Ponieważ bowiem kąt zewnętrzny BMC jest równy
wewnętrznym MDB, DBM, więc tym obu równy jest także kąt MBC. Jeżeli
zamiast kąta DBM weźmiemy kąt MBE, to będzie MBC równy dwu MBE, BDC, a
po odjęciu wspólnego MBE zostanie reszta BDC równa reszcie EBC.
Trójkąty zatem DCB i BCE są podobne. Przepołówmy proste DC i EC w H i F,
poprowadźmy HI, FG równoległe do poziomej CB i jak DH do HI, niech
będzie IH do HL; będzie zatem trójkąt IHL podobny IHD, któremu znów jest
podobny EGF, że zaś IH, GF są równe (bo każda jest połową BC), więc FE,
czyli FC jest równe HL, a dodając do obu FH, otrzymamy CH równe FL.
Jeżeli teraz wyobrazimy sobie połowę paraboli, przechodzącą przez H i
B, o wysokości HC, a wyniosłości HL, to jej amplituda będzie CB, które
jest równe podwojonemu HI, podczas gdy HI jest średnią proporcjonalną
między DH albo CH i HL; styczną więc do niej będzie DB wobec równości
CH i HD. Jeżeli znów wyobrazimy sobie parabolę, przechodzącą przez F i
B, z wyniosłością FL a wysokością FC, między którymi średnią
proporcjonalną jest FG, równe połowie poziomej CB, to tak samo
amplitudą jej będzie CB: styczną zaś do niej jest EB, bo EF i FC są
sobie równe. Ze zaś kąty DBC, EBC (nachylenia rzutu) różnią się
jednakowo od połowy kąta prostego, przeto twierdzenie jest
dowiedzione. Wysokość (rys. 120) GF paraboli FH ma się do wysokości CB
paraboli BD, jak wyniosłość BA do wyniosłości FE. Twierdzę, że
amplitudy HG i DC są sobie równe. Ponieważ bowiem pierwsza GF ma się do
drugiej CB, jak trzecia BA do czwartej FE, to prostokąt GVE
z pierwszej i czwartej jest równy prostokątowi CBA z
drugiej i trzeciej; zatem kwadraty równe tym prostokątom są sobie równe;
a że prostokątowi GFE jest równy kwadrat z połowy GH, a prostokątowi CBA
kwadrat z połowy CD, to te kwadraty, ich boki i zdwojenia tych boków są
sobie równe. Tymi ostatnimi zaś są amplitudy GH i CD, c.b.d.d.
Wysokość (rys. 120) GF paraboli FH ma się do wysokości CB
paraboli BD, jak wyniosłość BA do wyniosłości FE. Twierdzę, że
amplitudy HG i DC są sobie równe. Ponieważ bowiem pierwsza GF ma się do
drugiej CB, jak trzecia BA do czwartej FE, to prostokąt GVE
z pierwszej i czwartej jest równy prostokątowi CBA z
drugiej i trzeciej; zatem kwadraty równe tym prostokątom są sobie równe;
a że prostokątowi GFE jest równy kwadrat z połowy GH, a prostokątowi CBA
kwadrat z połowy CD, to te kwadraty, ich boki i zdwojenia tych boków są
sobie równe. Tymi ostatnimi zaś są amplitudy GH i CD, c.b.d.d. Niech będzie (rys. 121) AB podzielona w C. Twierdzę, że
kwadraty ze średnich proporcjonalnych między całą AB i częściami AC, CB
razem wzięte są równe kwadratowi z całej AB. Opiszmy półkole na AB i
wyprowadźmy z C prostopadłą CD, połączmy DA i DB. Jest więc DA średnią
między BA, AC a DB średnią między AB, BC, a suma kwadratów z linij DA,
BD jest równa kwadratowi z AB, bo kąt ADB w półkolu jest prosty; więc
twierdzenie jest dowiedzione.
Niech będzie (rys. 121) AB podzielona w C. Twierdzę, że
kwadraty ze średnich proporcjonalnych między całą AB i częściami AC, CB
razem wzięte są równe kwadratowi z całej AB. Opiszmy półkole na AB i
wyprowadźmy z C prostopadłą CD, połączmy DA i DB. Jest więc DA średnią
między BA, AC a DB średnią między AB, BC, a suma kwadratów z linij DA,
BD jest równa kwadratowi z AB, bo kąt ADB w półkolu jest prosty; więc
twierdzenie jest dowiedzione. Niech będzie (rys. 122) półparabola AB, której wyniosłością
jest DA, a wysokością AC, z których się składa prostopadła DC. Twierdzę,
że impet na półparaboli w B jest równy momentowi naturalnego spadku od D
do C. Przyjmijmy tę samą DC za miarę czasu i impetu i weźmy średnią
proporcjonalną między CD i CA równą CF. Niech będzie nadto CE średnia
proporcjonalna do DC i CA, to CF jest miarą czasu i momentu spadku
wzdłuż DA ze spoczynku w D, a CE czasem
i momentem spadku wzdłuż AC ze spoczynku w A, zaś przekątna EF momentem
z nich złożonym i to jest właśnie moment na półparaboli w B.
Że zaś DC podzielone jest w A, a CF i CE
są średnie między całym CD a jego częściami DA i AC, to będzie suma
kwadratów z tych średnich, na mocy powyższego lematu, równa kwadratowi z
całości; ale ta suma jest także równa kwadratowi z EF, a więc i linia EF
jest równa DC. Wynika stąd, że momenty spadku po DC i po półparaboli AB
w C i w B są równe, c.b.d.d.
Niech będzie (rys. 122) półparabola AB, której wyniosłością
jest DA, a wysokością AC, z których się składa prostopadła DC. Twierdzę,
że impet na półparaboli w B jest równy momentowi naturalnego spadku od D
do C. Przyjmijmy tę samą DC za miarę czasu i impetu i weźmy średnią
proporcjonalną między CD i CA równą CF. Niech będzie nadto CE średnia
proporcjonalna do DC i CA, to CF jest miarą czasu i momentu spadku
wzdłuż DA ze spoczynku w D, a CE czasem
i momentem spadku wzdłuż AC ze spoczynku w A, zaś przekątna EF momentem
z nich złożonym i to jest właśnie moment na półparaboli w B.
Że zaś DC podzielone jest w A, a CF i CE
są średnie między całym CD a jego częściami DA i AC, to będzie suma
kwadratów z tych średnich, na mocy powyższego lematu, równa kwadratowi z
całości; ale ta suma jest także równa kwadratowi z EF, a więc i linia EF
jest równa DC. Wynika stąd, że momenty spadku po DC i po półparaboli AB
w C i w B są równe, c.b.d.d. Niech będzie dany impet (rys. 123), określony długością
prostopadłej do poziomu AB i na poziomej dana amplituda BC. Należy
znaleźć wyniosłość półparaboli, której impet byłby równy AB a amplituda
BC. Z poprzedniego wynika, że połowa amplitudy BC jest średnią
proporcjonalną między wysokością a wyniosłością tejże półparaboli,
której impet według poprzedniego jest równy impetowi spadku wzdłuż AB,
ze spoczynku w A. Zatem AB tak ma być podzielone, aby prostokąt z jego
części był równy kwadratowi z połowy BC czyli z BD. Okazuje się tu, że
DB nie może być większe od połowy BA, bo prostokąt utworzony z części
jest największy, gdy części są równe. Przepołówmy zatem BA w E. Gdyby BD
było równe BE, zadanie byłoby rozwiązane: wysokością półparaboli byłoby
BE, a wyniosłością EA (i oto amplituda paraboli o podniesieniu równym
połowie kąta prostego jest największa, jak to było dowiedzione, ze
wszystkich opisanych przy jednakowym impecie). Gdy znów BD jest mniejsze
od połowy BA, to podzielić należy to ostatnie tak, aby prostokąt z jego
części był równy kwadratowi z DB. Opiszmy półkole na EA, od A odetnijmy
AF równe BD: i poprowadźmy FE, któremu równe odetnijmy EG. Będzie tedy
prostokąt BGA razem z kwadratem z EG równy kwadratowi z EA, któremu
także jest równa suma kwadratów z AF i FE. Jeżeli odejmiemy równe sobie
kwadraty z GE i FE, zostanie prostokąt BGA równy kwadratowi z AF albo z
BD; a linia BD jest średnią proporcjonalną między BG i GA. Wynika stąd,
że wysokość półparaboli o amplitudzie BC i impecie AB jest równa BG a
wyniosłość równa GA. Jeżeli odetniemy BI równe GA, to BI będzie
wysokością, a IA wyniosłością półparaboli IC. Na zasadzie dowiedzionego,
możemy to uczynić.
Niech będzie dany impet (rys. 123), określony długością
prostopadłej do poziomu AB i na poziomej dana amplituda BC. Należy
znaleźć wyniosłość półparaboli, której impet byłby równy AB a amplituda
BC. Z poprzedniego wynika, że połowa amplitudy BC jest średnią
proporcjonalną między wysokością a wyniosłością tejże półparaboli,
której impet według poprzedniego jest równy impetowi spadku wzdłuż AB,
ze spoczynku w A. Zatem AB tak ma być podzielone, aby prostokąt z jego
części był równy kwadratowi z połowy BC czyli z BD. Okazuje się tu, że
DB nie może być większe od połowy BA, bo prostokąt utworzony z części
jest największy, gdy części są równe. Przepołówmy zatem BA w E. Gdyby BD
było równe BE, zadanie byłoby rozwiązane: wysokością półparaboli byłoby
BE, a wyniosłością EA (i oto amplituda paraboli o podniesieniu równym
połowie kąta prostego jest największa, jak to było dowiedzione, ze
wszystkich opisanych przy jednakowym impecie). Gdy znów BD jest mniejsze
od połowy BA, to podzielić należy to ostatnie tak, aby prostokąt z jego
części był równy kwadratowi z DB. Opiszmy półkole na EA, od A odetnijmy
AF równe BD: i poprowadźmy FE, któremu równe odetnijmy EG. Będzie tedy
prostokąt BGA razem z kwadratem z EG równy kwadratowi z EA, któremu
także jest równa suma kwadratów z AF i FE. Jeżeli odejmiemy równe sobie
kwadraty z GE i FE, zostanie prostokąt BGA równy kwadratowi z AF albo z
BD; a linia BD jest średnią proporcjonalną między BG i GA. Wynika stąd,
że wysokość półparaboli o amplitudzie BC i impecie AB jest równa BG a
wyniosłość równa GA. Jeżeli odetniemy BI równe GA, to BI będzie
wysokością, a IA wyniosłością półparaboli IC. Na zasadzie dowiedzionego,
możemy to uczynić. Z poprzednio dowiedzionego wynika, że pociski z jednakowym impetem
wyrzucane, opisywać będą parabole, których sumy wyniosłości i wysokości
będą jednakowe. Wszystkie te sumy leżą przeto na pionowej zawartej między
temi samymi dwiema poziomymi. Niech będzie (rys. 124) do
poziomej CB prostopadła równa jej BA i poprowadźmy przekątną AC. Kąt ACB
będzie zatem połową prostego czyli 45 stopni. Przepołówmy prostopadłą
BA w D, to będzie DC tą półparabolą, która ma wyniosłość AD, a wysokość
DB; a jej impet w C jest ten sam, jak ciała spadającego ze spoczynku w
A wzdłuż AB, w punkcie B. Poprowadźmy AG równoległe do BC; dla
wszystkich innych półparabol tegoż samego impetu winny sumy wyniosłości
i wysokości mieścić się między AG i BC. Ponieważ dalej dowiedzione
zostało, że amplitudy tych półparabol, których styczne jednakowo nad lub
pod 45 stopniem są skierowane, są sobie równe, więc rachunek
przeprowadzony dla większych nachyleń służyć będzie i dla mniejszych.
Przyjmijmy także liczbę dziesięciu tysięcy części, jako największą
amplitudę półparaboli opisanej rzutem przy nachyleniu 45°, taka więc
będą linia BA i amplituda półparaboli BC. Obieramy zaś liczbę 10000,
bo użyjemy do rachunku tablicy stycznych, która daje tę liczbę jako
styczną kąta 45 stopni. Przystępując do dzieła, poprowadźmy CE pod kątem
ECB większym od kąta ACB (ale zawsze ostrym): mamy nakreślić półparabolę styczną do linii EC, której wyniosłość
razem z wysokością ma być równa AB. Z tablicy stycznych weźmiemy
długość stycznej BE kąta BCE i ta długość przepołowiona da nam punkt F.
Określamy następnie trzecią proporcjonalną do BF i do BI (połowy BC),
która koniecznie będzie większa od FA. Niech nią będzie FO.
Dla półparaboli więc wpisanej w trójkąt ECB, ze styczną CE i amplitudą
CB, otrzymujemy wysokość BF i wyniosłość FO. Ale suma BO przewyższa
odległość między równoległymi AG i BC, a tymczasem parabole nie mogą
przekraczać tych granic, gdyż tak szukana, jak i parabola DC opisywane są
pociskami wyrzucanymi z C z tym samym impetem. Szukać więc należy innej
paraboli, podobnej do znalezionej (bo pod kątem BCE mogą być opisane
niezliczone podobne do siebie większe lub mniejsze), której suma
wyniosłości i wysokości jest równa BA. Niech się więc ma OB do BA jak
amplituda BC do CR i otrzymamy CR amplitudę półparaboli opisanej przy
nachyleniu kąta BCE, której suma wyniosłości i wysokości mieści się
między poziomem! GA i CB, co właśnie było żądane. Postępowanie zatem
będzie takie.
Z poprzednio dowiedzionego wynika, że pociski z jednakowym impetem
wyrzucane, opisywać będą parabole, których sumy wyniosłości i wysokości
będą jednakowe. Wszystkie te sumy leżą przeto na pionowej zawartej między
temi samymi dwiema poziomymi. Niech będzie (rys. 124) do
poziomej CB prostopadła równa jej BA i poprowadźmy przekątną AC. Kąt ACB
będzie zatem połową prostego czyli 45 stopni. Przepołówmy prostopadłą
BA w D, to będzie DC tą półparabolą, która ma wyniosłość AD, a wysokość
DB; a jej impet w C jest ten sam, jak ciała spadającego ze spoczynku w
A wzdłuż AB, w punkcie B. Poprowadźmy AG równoległe do BC; dla
wszystkich innych półparabol tegoż samego impetu winny sumy wyniosłości
i wysokości mieścić się między AG i BC. Ponieważ dalej dowiedzione
zostało, że amplitudy tych półparabol, których styczne jednakowo nad lub
pod 45 stopniem są skierowane, są sobie równe, więc rachunek
przeprowadzony dla większych nachyleń służyć będzie i dla mniejszych.
Przyjmijmy także liczbę dziesięciu tysięcy części, jako największą
amplitudę półparaboli opisanej rzutem przy nachyleniu 45°, taka więc
będą linia BA i amplituda półparaboli BC. Obieramy zaś liczbę 10000,
bo użyjemy do rachunku tablicy stycznych, która daje tę liczbę jako
styczną kąta 45 stopni. Przystępując do dzieła, poprowadźmy CE pod kątem
ECB większym od kąta ACB (ale zawsze ostrym): mamy nakreślić półparabolę styczną do linii EC, której wyniosłość
razem z wysokością ma być równa AB. Z tablicy stycznych weźmiemy
długość stycznej BE kąta BCE i ta długość przepołowiona da nam punkt F.
Określamy następnie trzecią proporcjonalną do BF i do BI (połowy BC),
która koniecznie będzie większa od FA. Niech nią będzie FO.
Dla półparaboli więc wpisanej w trójkąt ECB, ze styczną CE i amplitudą
CB, otrzymujemy wysokość BF i wyniosłość FO. Ale suma BO przewyższa
odległość między równoległymi AG i BC, a tymczasem parabole nie mogą
przekraczać tych granic, gdyż tak szukana, jak i parabola DC opisywane są
pociskami wyrzucanymi z C z tym samym impetem. Szukać więc należy innej
paraboli, podobnej do znalezionej (bo pod kątem BCE mogą być opisane
niezliczone podobne do siebie większe lub mniejsze), której suma
wyniosłości i wysokości jest równa BA. Niech się więc ma OB do BA jak
amplituda BC do CR i otrzymamy CR amplitudę półparaboli opisanej przy
nachyleniu kąta BCE, której suma wyniosłości i wysokości mieści się
między poziomem! GA i CB, co właśnie było żądane. Postępowanie zatem
będzie takie. Niech będzie (rys. 125) dana amplituda BC. Impet zaś, który
przyjmujemy, że jest wciąż jednakowy, niech będzie OB, jest to suma
wysokości i wyniosłości. Mamy oznaczyć i wydzielić samą wysokość.
Ponieważ BO ma być tak podzielone, aby prostokąt z jego części był
równy kwadratowi z połowy amplitudy BC, to punkt podziału przypadnie w
F. Przepołówmy OB i BC w D i I. Kwadrat więc z IB jest równy
prostokątowi BFO, podczas gdy kwadrat z DO równy jest temuż prostokątowi
razem z kwadratem z FD. Jeżeli zatem od kwadratu z DO odejmiemy kwadrat
z BI, równy prostokątowi BFO, to pozostanie kwadrat z FD, a dodawszy do
jego boku FD długość BD, otrzymamy szukaną wysokość BF. Postępuje się
zatem w ten sposób. Od kwadratu z połowy BO odejmuje się kwadrat z BI, z
reszty wyciąga się pierwiastek kwadratowy, dodaje do niego BD i
otrzymuje szukaną wysokość BF. Przykład. Szukamy wysokościpółparaboli
opisanej przy 55 stopniach podniesienia. Amplituda z poprzedniej
tablicy jest 9396, połowa jej 4698, a kwadrat z tej połowy 22071204; to
odjęte od kwadratu z połowy BA, który jest zawsze jednaki, mianowicie
25000000, daje resztę 2928796, z której pierwiastek kwadratowy wynosi
prawie 1710. Dodany do połowy BA, to jest do 5000, daje 6710 i taka jest
wysokość BF. Nie będzie zbyteczne' ułożenie trzeciej tablicy,
zawierającej wysokości i wyniosłości półparabol, mających jednakową
amplitudę.
Niech będzie (rys. 125) dana amplituda BC. Impet zaś, który
przyjmujemy, że jest wciąż jednakowy, niech będzie OB, jest to suma
wysokości i wyniosłości. Mamy oznaczyć i wydzielić samą wysokość.
Ponieważ BO ma być tak podzielone, aby prostokąt z jego części był
równy kwadratowi z połowy amplitudy BC, to punkt podziału przypadnie w
F. Przepołówmy OB i BC w D i I. Kwadrat więc z IB jest równy
prostokątowi BFO, podczas gdy kwadrat z DO równy jest temuż prostokątowi
razem z kwadratem z FD. Jeżeli zatem od kwadratu z DO odejmiemy kwadrat
z BI, równy prostokątowi BFO, to pozostanie kwadrat z FD, a dodawszy do
jego boku FD długość BD, otrzymamy szukaną wysokość BF. Postępuje się
zatem w ten sposób. Od kwadratu z połowy BO odejmuje się kwadrat z BI, z
reszty wyciąga się pierwiastek kwadratowy, dodaje do niego BD i
otrzymuje szukaną wysokość BF. Przykład. Szukamy wysokościpółparaboli
opisanej przy 55 stopniach podniesienia. Amplituda z poprzedniej
tablicy jest 9396, połowa jej 4698, a kwadrat z tej połowy 22071204; to
odjęte od kwadratu z połowy BA, który jest zawsze jednaki, mianowicie
25000000, daje resztę 2928796, z której pierwiastek kwadratowy wynosi
prawie 1710. Dodany do połowy BA, to jest do 5000, daje 6710 i taka jest
wysokość BF. Nie będzie zbyteczne' ułożenie trzeciej tablicy,
zawierającej wysokości i wyniosłości półparabol, mających jednakową
amplitudę.
 Zadanie V. Podanie XIV
Zadanie V. Podanie XIV SAGREDO : Wybornie rozumujecie i przyznacie niewątpliwie, że
jakkolwiek mała będzie siła ciała poruszającego, to jednak pokona jak
największy opór, skoro tylko powiększenie prędkości przewyższy ubytek
siły i ciężkości. Ale przejdźmy do przypadku liny. A objaśniając na
rysunku, (rys. 124) niech linę przedstawia linia AB,
przechodząca przez dwa punkty stałe AB, na której końcach są zawieszone
wielkie ciężary C, D, które ciągnąc z wielką siłą utrzymają linę
wyciągniętą prosto, o ile przyjmujemy ją jako nieważką. Lecz jeżeli w
jej środkowym punkcie E zawiesimy jakikolwiek mały ciężar H, to linia
AB się ugnie i zejdzie do F, a wydłużając się wskutek tego zmusi do
podniesienia się dwa wielkie ciężary C, D: co w ten sposób może być
dowiedzione. Z punktów A i B, jako środków, opisujemy dwie ćwiartki koła
EFG i ELM; a ponieważ promienie AI i BL są równe AE i EB, to FI i FL będą
wydłużeniami tj. przewyżkami AF i FB ponad AE i EB; one zatem
wyznaczają podniesienia ciężarów C i D, gdy ciężar H zdoła obniżyć linę
do F, to zaś może nastąpić wtedy, gdy stosunek linii EF, tj. obniżenia
ciężaru H, do linii FI określającej podniesienie ciężarów C i D, będzie
większy od stosunku obu ciężarów C i D do ciężaru H. Ale to nastąpi
koniecznie, chociażby ciężary C i D były jak największe, a ciężar H jak
najmniejszy. Albowiem przewyżka C i D nad H nie jest tak wielka, aby nie
mogła być przedstawiona przez przewyżkę stycznej EF nad kawałkiem
siecznej FI. O tym zaś przekonamy się w tym sposób: niech będzie koło o
średnicy GI i jaki jest stosunek ciężarów C i D do ciężaru H, taki niech
będzie stosunek BO do innej linii C, większej od D, tak że stosunek BO
do D będzie większy od stosunku BO do C; weźmy następnie trzecią
proporcjonalną do OB i D, mianowicie BE i jak OE do EB, tak niech się ma
średnica GI do przedłużenia IF, a przez koniec F poprowadźmy styczną
FN. A ponieważ tak się ma OE do EB, jak GI do FI, to
będzie się miała suma OB do BE, jak GF do FI. Ale między OB i BE średnią
proporcjonalną jest D, a między GF i FI średnią jest NF; więc tak się ma
NF do FI, jak OB do D i stosunek ten jest większy od stosunku ciężarów
C i D do H. Stosunek więc obniżenia, czyli prędkości ciężaru H, do
podniesienia, czyli prędkości ciężarów C i D, jest większy od stosunku
ciężarów C i D do ciężaru H; zatem H musi się obniżać, a linia AB
odchylać od prostej poziomej. Co zaś dzieje się z nieważką liną AB przy
malym obciążeniu w B, to stanie się z ciężką liną bez dodawania innego
ciężaru, gdyż zawieszony zostaje ciężar tworzywa samej liny AB.
SAGREDO : Wybornie rozumujecie i przyznacie niewątpliwie, że
jakkolwiek mała będzie siła ciała poruszającego, to jednak pokona jak
największy opór, skoro tylko powiększenie prędkości przewyższy ubytek
siły i ciężkości. Ale przejdźmy do przypadku liny. A objaśniając na
rysunku, (rys. 124) niech linę przedstawia linia AB,
przechodząca przez dwa punkty stałe AB, na której końcach są zawieszone
wielkie ciężary C, D, które ciągnąc z wielką siłą utrzymają linę
wyciągniętą prosto, o ile przyjmujemy ją jako nieważką. Lecz jeżeli w
jej środkowym punkcie E zawiesimy jakikolwiek mały ciężar H, to linia
AB się ugnie i zejdzie do F, a wydłużając się wskutek tego zmusi do
podniesienia się dwa wielkie ciężary C, D: co w ten sposób może być
dowiedzione. Z punktów A i B, jako środków, opisujemy dwie ćwiartki koła
EFG i ELM; a ponieważ promienie AI i BL są równe AE i EB, to FI i FL będą
wydłużeniami tj. przewyżkami AF i FB ponad AE i EB; one zatem
wyznaczają podniesienia ciężarów C i D, gdy ciężar H zdoła obniżyć linę
do F, to zaś może nastąpić wtedy, gdy stosunek linii EF, tj. obniżenia
ciężaru H, do linii FI określającej podniesienie ciężarów C i D, będzie
większy od stosunku obu ciężarów C i D do ciężaru H. Ale to nastąpi
koniecznie, chociażby ciężary C i D były jak największe, a ciężar H jak
najmniejszy. Albowiem przewyżka C i D nad H nie jest tak wielka, aby nie
mogła być przedstawiona przez przewyżkę stycznej EF nad kawałkiem
siecznej FI. O tym zaś przekonamy się w tym sposób: niech będzie koło o
średnicy GI i jaki jest stosunek ciężarów C i D do ciężaru H, taki niech
będzie stosunek BO do innej linii C, większej od D, tak że stosunek BO
do D będzie większy od stosunku BO do C; weźmy następnie trzecią
proporcjonalną do OB i D, mianowicie BE i jak OE do EB, tak niech się ma
średnica GI do przedłużenia IF, a przez koniec F poprowadźmy styczną
FN. A ponieważ tak się ma OE do EB, jak GI do FI, to
będzie się miała suma OB do BE, jak GF do FI. Ale między OB i BE średnią
proporcjonalną jest D, a między GF i FI średnią jest NF; więc tak się ma
NF do FI, jak OB do D i stosunek ten jest większy od stosunku ciężarów
C i D do H. Stosunek więc obniżenia, czyli prędkości ciężaru H, do
podniesienia, czyli prędkości ciężarów C i D, jest większy od stosunku
ciężarów C i D do ciężaru H; zatem H musi się obniżać, a linia AB
odchylać od prostej poziomej. Co zaś dzieje się z nieważką liną AB przy
malym obciążeniu w B, to stanie się z ciężką liną bez dodawania innego
ciężaru, gdyż zawieszony zostaje ciężar tworzywa samej liny AB.