DZIEJE RELIGII, FILOZOFII I NAUKI
indeks | antologia religijna | antologia filozoficzna | filozofia nauki
Wojciech Sady
Henri Poincaré o prostych faktach, poczuciu piękna, zasadach i prawach doświadczalnych
Spór o racjonalność naukową: od Poincarégo do Laudana, wyd. 2 popr. i rozsz. Toruń: Wyd. UMK 2014, rozdz. 1
1. Aksjomaty geometrii jako konwencje
2. O roli prostych faktów i
poczucia piękna
3. Zasady i prawa
doświadczalne
4.Czy wyniki doświadczeń
mogą zdetronizować zasady?
5.Czy i w jakim sensie
nauka poznaje świat?
6.O wartości nauki
Bibliografia
Henri Poincaré urodził się w 1854 r. w Nancy we Francji. Gdy miał pięć lat zachorował na dyfteryt; ocalony przez ojca – który był lekarzem i wykładowcą miejscowej L’Ecole de Médicine – cierpiał czas jakiś na zaburzenia mowy i w szkole musiał korzystać z pomocy siostry, z którą porozumiewał się na migi. Zadziwiał nauczycieli wybitnymi zdolnościami i wszechstronnością zainteresowań. Jako trzynastolatek, pobudzony wizytą w Paryżu i podsuniętymi przez ojca książkami, zrozumiał, że w konstrukcji państwa nie ma niczego koniecznego, a zależy ona od umowy społecznej – podobno te rozmyślania, przeniesione na teren matematyki i przyrodoznawstwa, doprowadziły go po latach do sformułowania podstawowych zasad konwencjonalistycznej filozofii i metodologii nauki. Ponoć też nacisk, jaki kładł na rolę poczucia harmonii i piękna w pracy naukowca, miał swe źródła w przejętej od matki miłości przyrody. A wreszcie trudne doświadczenia moralne, jakich doznał, pozostając przy boku ojca w Nancy podczas wojny francusko-pruskiej w 1870 r., inspirowały potem jego uwagi o roli zasad moralnych w życiu uczonych. W szkolnym teatrze odgrywał sztuki, które pisywał wspólnie z przyjacielem. Studiował matematykę i fizykę w elitarnej paryskiej L’Ecole Normale Supérieur, gdzie później wykładał. Był też profesorem Sorbony, członkiem Akademii Francuskiej. Zmarł w pełni sił twórczych w 1912 r.
Poincaré to jeden z najwybitniejszych matematyków i fizyków końca XIX w. Do historii matematyki przeszedł jako współtwórca współczesnej topologii, czyli teorii tych własności przestrzeni, które są niezmiennicze ze względu na przekształcenia homeomorficzne. Jako fizyk ogłosił m.in. ważne dla astronomii prace o problemie trzech ciał. W 1905 r. opublikował artykuł Sur la Dynamique de l’Electron, w którym poprawił i uzupełnił teorię ogłoszoną rok wcześniej przez Henrika Lorentza, otrzymując w rezultacie układ równań dokładnie równoważny układowi podanemu niezależnie w tym samym roku przez Einsteina w artykule O elektrodynamice ciał w ruchu. Chodzi oczywiście o równania szczególnej teorii względności. Był więc Poincaré nie tylko świadkiem, ale i współtwórcą wielkiej rewolucji, która na początku XX w. skierowała fizykę na nowe tory. Nadawał jednak nowym równaniom starą – opartą na tezie o istnieniu podległego prawom mechaniki eteru – interpretację i do końca życia nie pojął znaczenia przemian, w których uczestniczył.
Jego pierwsza praca filozoficzna Sur les hypothèses fondamentales de la géométrie (1887) dotyczyła natury geometrii; wkrótce potem w Leçon sur la théorie mathématique de la lumière (1889) rozszerzył sformułowane tam tezy na fizykę. Prawie wszystkie artykuły, w których w spopularyzowanej formie prowadził refleksje dotyczące ówczesnego stanu fizyki i matematyki, przewidywał ich przyszły rozwój, a przede wszystkim przedstawiał poglądy na temat natury wiedzy naukowej, jej genezy i prawomocności, a także sposobów uprawiania nauk, zebrał w trzech książkach. Były to kolejno Nauka i hipoteza (1902), Wartość nauki (1905) i Nauka i metoda (1908). Pośmiertnie ogłoszono jeszcze Deniéres pensées (Ostatnie myśli, 1913). Filozoficznie ważna jest przede wszystkim pierwsza książka i końcowe partie drugiej. Są to luźne zbiory esejów pisanych bez dbałości o systematyczność wywodów czy precyzję sformułowań; co więcej, Poincaré w międzyczasie modyfikował swoje poglądy. Poniższy tekst jest próbą zebrania jego wywodów w możliwie koherentną całość, co wymagało niekiedy dość ryzykownych interpretacji.
1. Aksjomaty geometrii jako konwencje
Punktem wyjścia filozoficznych rozważań Poincarégo była refleksja nad istnieniem alternatywnych systemów geometrii i wspomnianych powyżej propozycjach empirycznego rozstrzygnięcia, który z nich jest prawdziwy – czyli zgodny z rzeczywistością. Prowadzi to do pytania o naturę twierdzeń geometrycznych. W ich powstaniu niepodważalną rolę odgrywa doświadczenie (wszak w szkole uczy się geometrii podsuwając dzieciom rysunki i zachęcając je, by same rysowały figury, mierzyły długości, kąty itd.). Ale gdyby geometria była nauką doświadczalną, nie mogłaby ani być ścisła (bo wszelkie rysunki czy empiryczne pomiary obarczone są błędami), ani budzić w nas poczucia pewności (bo jeśli z doświadczenia wiem, że kruki widziane dotąd kruki były czarne, to łatwo mi sobie wyobrazić, że następny ujrzany przeze mnie kruk będzie żółty).
Widzimy, że doświadczenie odgrywa
niezbędną rolę w powstaniu geometrii; byłoby jednak błędem wnioskować z tego, że
geometria jest nauką eksperymentalną, choćby tylko częściowo.
Gdyby była ona nauką eksperymentalną,
byłaby tylko przybliżoną i prowizoryczną. I to jak nieprecyzyjnie przybliżoną!
Geometria byłaby jedynie nauką o ruchach
ciał stałych; w rzeczywistości zajmuje się ona jednak ciałami naturalnymi, jej
przedmiotem są pewne ciała idealne, absolutnie niezmienne, które są tylko ich
uproszczonym i bardzo odległym obrazem.
Pojęcie tych idealnych ciał wywodzi się
całkowicie z naszego umysłu i doświadczenie jest jedynie okazją, która nas
pobudza, by je z niego wyprowadzić.
Natomiast przedmiotem geometrii jest
badanie szczególnej „grupy”; ale ogólne pojęcie grupy istnieje odwiecznie w
naszym umyśle co najmniej potencjalnie. Narzuca się nam ono nie jako forma
naszej zmysłowości, lecz jako forma naszej zdolności rozumienia.
Spośród
wszystkich grup możliwych trzeba wybrać tę, która będzie, że tak powiem,
wzorcem, do którego będziemy odnosili
zjawiska przyrodnicze.
Doświadczenie wskazuje nam drogę w tym
wyborze, ale nam go nie narzuca; pozwala nam ono rozpoznać nie to, która
geometria jest najbardziej prawdziwa, ale która jest najbardziej
dogodna (1902, § IV)
Powstaje tu pytanie o status twierdzeń teorii grup: czy są to sądy syntetyczne a priori w sensie Kanta? Na to jasnej odpowiedzi Poincaré nie dał. Traktował pojęcie grupy jako swoiste ograniczenie dla naszej wyobraźni, która pobudzana przez doświadczenie tworzy systemy geometryczne:
(…) nasza przestrzeń euklidesowa, która jest właściwym przedmiotem geometrii, została wybrana ze względu na wygodę spośród pewnej liczby typów, które istnieją odwiecznie w naszym umyśle i zwą się grupami (1905, § X,4).
Same aksjomaty geometrii nie są, podkreślał autor Nauki i hipotezy, sądami syntetycznymi a priori – bo wtedy nie mogłyby istnieć systemy alternatywne. Nie są też sądami syntetycznymi a posteriori, bowiem niezależnie od pierwotnej inspiracji doświadczeniem nie ma możliwości empirycznego rozstrzygnięcia, która z geometrii – Euklidesa, Łobaczewskiego czy Riemanna – jest prawdziwa, a w każdym razie rozstrzygnięcie nie może nastąpić w sposób tak prosty, jak sądził Gauss. Wyobraźmy sobie, że zgodnie z radami tego ostatniego ktoś zmierzył kąty, pod jakimi z trzech odległych szczytów górskich widać dwa pozostałe. Taki pomiar – zauważał Poincaré – opiera się na szeregu hipotez z zakresu nie geometrii, ale fizyki, m.in. na założeniu, iż światło rozchodzi się po liniach prostych. Gdyby więc suma zmierzonych kątów okazała się np. większa od 1800, to mogłoby to świadczyć o tym, że 1) przestrzeń fizyczna w badanym obszarze ma charakter riemannowski że 2) światło w trakcie pomiarów nie rozchodziło się po liniach prostych, że 3) urządzenia do pomiaru kątów uległy z jakiegoś powodu deformacji itd.
Poincaré ilustrując to szeregiem sugestywnych przykładów dowodził, że możemy przyjąć dowolny – byle niesprzeczny – system geometryczny, o ile tylko odpowiednio dobierzemy towarzyszące mu prawa fizyki. A zatem nie ma sensu mówić o klasycznie rozumianej prawdziwości geometrii. Aksjomaty geometryczne same w sobie nie opisują przestrzeni, w której żyjemy, są to natomiast definicje w przebraniu. Mówiąc np. „suma kątów w trójkącie wynosi 180º”, nie stwierdzam własności pewnych fizycznych czy idealnych obiektów, ale mówię, że trójkątem nazywamy taką figurę, której suma kątów jest równa 180º. I jeśli zmierzywszy kąty figury o trzech bokach otrzymam inną wartość, to – na mocy definicji – stwierdzę, że figura ta (wbrew pozorom) nie jest trójkątem.
Pewniki geometryczne nie są więc ani
sądami syntetycznymi a priori,
ani faktami eksperymentalnymi.
Są to konwencje;
naszym wyborem, spośród wszystkich konwencji możliwych, kierują
fakty eksperymentalne; wybór ten jednak jest swobodny,
a ogranicza go tylko konieczność unikania wszelkiej sprzeczności. W ten sposób
postulaty mogą pozostać ściśle
prawdziwe, gdyby nawet prawa eksperymentalne, które zdecydowały o ich przyjęciu,
były tylko przybliżone.
Innymi
słowy, pewniki geometrii (nie
mówię o pewnikach arytmetyki) są jedynie ukrytymi definicjami.
Wobec tego, co należy myśleć o pytaniu:
czy geometria euklidesowa jest prawdziwa?
Pytanie to nie ma żadnego sensu.
To tyle, co
zapytać, czy system metryczny jest prawdziwy, a dawne miary fałszywe (…). Jedna
geometria nie może być prawdziwsza od drugiej; może być ona jedynie
wygodniejsza (1902, § II,3).
Systemy geometrii są wytworami naszej wyobraźni, a stosujemy je do opisu położeń i ruchów ciał w naszym otoczeniu. Jeśli twierdzenia jednego z systemów uważamy za obowiązujące, to jest tak na mocy umowy – konwencji – którą podświadomie, a co najwyżej półświadomie zawierają członkowie wspólnoty uczonych.
To wyjaśnia poczucie pewności, jakie wzbudzają w nas aksjomaty wspólnotowo przyjętej geometrii (zwłaszcza gdy brak jest systemów alternatywnych). Rozważmy dwa przypadki. Na podstawie dotychczasowych doświadczeń sądzimy, że Słońce jutro wzejdzie, ale pewności co do tego mieć nie możemy. Natomiast możemy być pewni, że pionek szachowy bije na ukos. Oczywiście nie na tej podstawie, że obserwowaliśmy tysiące partii szachów i uogólniliśmy (tak jak w przypadku wschodów Słońca) wyniki naszych spostrzeżeń – wtedy znów nie moglibyśmy mieć pewności. Mamy pewność, gdyż sami reguły gry w szachy ustaliliśmy. Źródłem pewności jest podjęta wspólnie przez ludzi decyzja, ustanawiająca reguły gry. Ale znaczy to, że nie ma sensu pytać, czy reguły gry w szachy są prawdziwe. Można pytać jedynie, czy ukonstytuowana przez nie gra jest interesująca, czy nie trwa za długo itd. Jedynym ograniczeniem jest wymóg niesprzeczności: nie dałoby się grać gdyby pewne ruchy był dozwolone przez którąś z przyjętych reguł, a zakazane przez inną.
Do problemu wyboru systemu geometrii jeszcze powrócimy, przy okazji warto wspomnieć o odmiennym poglądzie Poincarégo na temat natury arytmetyki. Tu podstawowym narzędziem dowodzenia ogólnych twierdzeń jest zasada indukcji matematycznej głosząca, iż jeśli jakieś twierdzenie jest prawdziwe dla n = 1 i z założenia, że jest prawdziwe dla dowolnego n wynika, że jest prawdziwe dla n + 1, to twierdzenie to jest prawdziwe dla każdego n. Nie da się tej zasady wywieść z doświadczenia (nie jest więc empiryczna), nie da się jej sprowadzić do zasady sprzeczności (nie jest więc analityczna), Poincaré nie uznaje jej też za konwencję, ale za sąd syntetyczny a priori:
[Reguła rozumowania rekurencyjnego]
stanowi prawdziwy typ sądu syntetycznego a priori.
Z drugiej strony, nie można by nawet myśleć o dopatrywaniu się w niej konwencji,
jak przy niektórych postulatach geometrii.
Dlaczegóż więc sąd ten narzuca się nam z
nieodpartą koniecznością? Dlatego, że jest ona potwierdzeniem potęgi umysłu,
który czuje się zdolny do zrozumienia nieograniczonego powtarzania się tego
samego aktu, gdy tylko akt ten raz jeden jest możliwy. Potęga ta daje umysłowi
intuicję bezpośrednią, a doświadczenie może być dla niego tylko sposobnością do
posłużenia się nią i przez to uświadomienia jej sobie (1902,
§
I,6).
W Nauce i metodzie Poincaré krytykuje w związku z tym próby zredukowania matematyki do logiki podejmowane przez Fregego i Russella (a przy okazji też formalizm Hilberta):
I w samym dowodzeniu logika nie jest wszystkim; prawdziwe rozumowanie matematyczne jest faktycznie indukcją, różną pod wieloma względami od indukcji fizycznej, ale przechodzącą jak ona od szczegółu do ogółu. Wszelkie wysiłki, dokonane w celu obalenia tego porządku i sprowadzenia indukcji matematycznej do reguł logiki, skończyły się jedynie niepowodzeniem, źle zamaskowanym przez użycie języka niedostępnego dla laika (1908, ks. IV, Wnioski).
2. O roli prostych faktów i poczucia piękna
Jak powiedziano, Poincaré szybko rozszerzył wyniki swych refleksji nad naturą systemów geometrii na nauki przyrodnicze jako całość. Dobrze będzie przedstawić tę część jego poglądów, zaczynając od momentu, w którym naukowcy formułują prawa lub teorie.

Załóżmy, że chcemy poznać fizyczne własności powietrza i w tym celu obserwujemy zjawiska atmosferyczne. Rezultat takich zabiegów będzie zapewne aż nadto skromny, a to dlatego, iż zjawiska te są niesłychanie skomplikowane: ogromna liczba czynników wpływa na ich przebieg. Istotny postęp osiągnięto dopiero wtedy, gdy poczęto badać fakty proste, najczęściej wytwarzane sztucznie w laboratorium. Tak więc Robert Boyle sporządził w 1662 r. rurkę szklaną, taką jak na rysunku; w jej zamkniętym końcu była uwięziona przez wlaną do rurki rtęć pewna ilość powietrza, dzięki czemu nie przybywało i nie ubywało go, a w wyniku wymiany ciepła z otoczeniem zachowywało ono stałą temperaturę. Dolewając rtęci przez otwarty koniec rurki, Boyle zwiększał stopniowo ciśnienie badanego powietrza, które mierzył, porównując różnice poziomów rtęci w obu jej ramionach, a jednocześnie mierzył zajmowaną przez powietrze objętość.
Uzyskane rezultaty przedstawił w postaci tabelki i na tym pracę zakończył; był bowiem zwolennikiem skrajnego empiryzmu, a zatem wrogiem wszelkich uogólnień czy wyjaśnień. Nie zrobił tego, co zdaniem Poincarégo uczynić powinien: nie przeszedł od jednostkowych faktów do ogólnych praw.
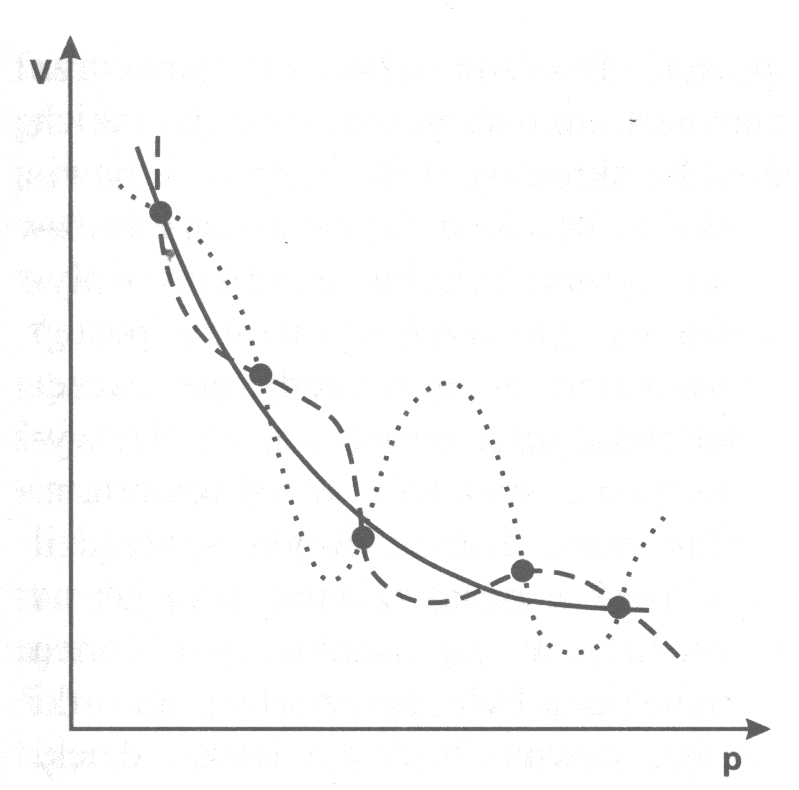
Uczynił to wkrótce Townley, my zaś spróbujemy zrekonstruować jego postępowanie, dla większej przejrzystości prezentując wyniki na wykresie. Załóżmy, że tabelka Boyle’a zawierała pięć wyników pomiarów objętości V powietrza w zależności od wartości ciśnienia p. Niezależnie od tego, jak wiele tych punktów na wykresie się znajdzie (zawsze ich liczba będzie skończona), możemy przeprowadzić przez nie nieskończenie wiele różnych krzywych. Townley wybrał tę, którą zaznaczono linią ciągłą, a która wyraża się wzorem V = c / p, gdzie c – pewna stała (ta formuła znana jest dziś jako prawo Boyle’a–Mariotte’a). Dlaczego? Bo jest ona najprostsza. A co znaczy „najprostsza”? Na to pytanie brak odpowiedzi słownej, rozstrzyga je jedynie poczucie harmonii i piękna. Jeśli nam tego poczucia brakuje, to nie jesteśmy zdolni do uprawiania nauki, a w szczególności do ustalania ogólnych praw na podstawie opisów pewnej liczby jednostkowych faktów (prostych).
Naukowcy zaczynają dociekania od poszukiwania prostych faktów, wiodących do ustalania prostych zależności, czyli praw. Tak jak nie ma ogólnego kryterium prostoty prawa, tak też nie ma uniwersalnego kryterium prostoty faktu. Intuicyjnie rzecz biorąc, do miana faktu prostego może pretendować sytuacja, na którą składa się niewiele elementów oddziałujących ze sobą na niewiele sposobów lub taka, że pewne oddziaływania można „w pierwszym przybliżeniu” pominąć. Tocząc kulki, wykonane z materiałów o dużym ciężarze właściwym, po gładkiej, wyskalowanej desce, Galileusz odkrył prawo spadku swobodnego. Newton odkrył prawo grawitacji, analizując ruchy planet, które poruszają się w próżni pod działaniem praktycznie jednej siły, jaką wywiera na nie Słońce (skutki wzajemnego przyciągania planet mieściły się w owym czasie w granicach błędów pomiarowych).
Z dzisiejszego punktu widzenia fakty badane przez Boyle’a nie były proste w określonym przed chwilą sensie: powietrze składa się z ogromnej liczby cząstek znajdujących się w nieustannym ruchu i zderzających co chwila ze sobą. Były one natomiast proste w sensie statystycznym: obserwujemy makroskopowy rezultat olbrzymiej ilości mikroskopowych zderzeń, a całościowy rezultat, podległy prawom wielkich liczb, wyraża się nader prostym wzorem matematycznym.
Nie możemy wiedzieć z góry, które fakty są proste. Obserwując kulkę staczającą się po gładkiej powierzchni nie widzimy, pod działaniem jakich i ilu sił ona się porusza (w ogóle nie widzimy, iż porusza się pod działaniem jakichś sił). Fakt, który sprawia wrażenie prostego, może – z perspektywy osiągniętej później wiedzy – okazać się złożony i na odwrót. Musimy szukać po omacku, dając pierwszeństwo, radzi Poincaré, „faktom, które wydają się proste, przed tymi, w których nasze niedoskonałe oko rozróżnia odmienne elementy” (1908, § I.I). Jedną z – zawodnych – oznak prostoty jest powtarzalność faktów: w tych samych (mniej więcej) okolicznościach powinniśmy obserwować te same (mniej więcej) efekty. Inną – zawodną – oznaką będzie właśnie możliwość ustalenia prostych zależności między wielkościami, za pomocą których charakteryzujemy badany fakt – czyli odkrycia praw.
Wyniki doświadczeń nie narzucają nam praw i narzucać nie mogą, choćby dlatego, że to my wcześniej dokonujemy selekcji, oddzielając wyniki „istotne” i „pouczające” od „złożonych” i „zbyt skomplikowanych”, a wreszcie od „przypadkowych” i „bezużytecznych”. Ale wyniki niektórych doświadczeń sugerują nam prawa: wybieramy jako kandydatki na prawa najprostsze z zależności, które zgadzają się z wybranym zbiorem faktów. Dodatkowe ograniczenia narzuca zasada niesprzeczności.
Powiedzieć, że wybieramy najprostsze (spośród niesprzecznych) prawo zgodne z faktami, to za mało. Sformułowane zgodnie z zasadami piękna i harmonii prawo zwykle poprawia wyniki doświadczeń. Przyjrzyjmy się zamieszczonemu powyżej rysunkowi: widać, że wybrana krzywa – w przeciwieństwie do obu pozostałych – wcale nie przechodzi dokładnie przez punkty doświadczalne. I tak jest zawsze, albowiem każdy pomiar obarczony jest błędem. Błędy dzielimy na systematyczne i statystyczne. Te pierwsze polegają na tym, że pewne czynniki, związane z warunkami doświadczalnymi, w systematyczny sposób zmniejszają lub zwiększają mierzone wartości (np. włączenie amperomierza do układu zmniejsza natężenie płynącego wcześniej prądu). Błędy systematyczne udaje się niekiedy oszacować (o ile pozwala na to stan naszej wiedzy) i odjąć od wyniku. Błędy statystyczne objawiają się tym, że wartości mierzone są rozrzucone, wskutek wpływu różnych niekontrolowanych czynników, wokół wartości „rzeczywistej”; można je szacować metodami rachunku prawdopodobieństwa o ile dysponujemy wieloma pomiarami tej samej wielkości lub przeprowadzamy krzywą założonego typu przez punkty doświadczalne metodą najmniejszych kwadratów. Prawo Boyle’a–Mariotte’a sformułowano jeszcze inaczej: zakładając, że wyniki pomiarów obarczone są jakimiś błędami, stwierdzono, iż jeśli mimo to układają się one w pobliżu krzywej, zapisywalnej za pomocą prostej funkcji typu y = c / x, to funkcja ta wyraża poszukiwane prawo.
Naukowcy zwykle borykają się z zagadnieniami o wiele poważniejszymi niż problem przeprowadzenia krzywej przez zbiór punktów. Mnóstwo faktów charakteryzowanych jest przez wiele parametrów jednocześnie, a nie wszystkie dają się bezpośrednio mierzyć; często też trzeba domyślać się istnienia bytów niepodległych obserwacji (na przykład zbudować model atomu na podstawie widma jego promieniowania). Choć Poincaré tego konsekwentnie nie czyni, dobrze jest rozróżnić prawa doświadczalne i teorie. Prawem doświadczalnym jest np. prawo Boyle’a–Mariotte’a, stanowiące indukcyjne uogólnienie wyników pomiarów (ujętych w stworzony przez nas system pojęciowy). Teorią jest np. korpuskularno-kinetyczna teoria gazów, która mówi o bytach i procesach nieobserwowalnych (gaz składa się z atomów poruszających się ruchami chaotycznymi i zderzających się sprężyście), nie mogła zatem powstać jako uogólnienie wyników doświadczeń. Teorie, postulując istnienie bytów nieobserwowalnych, wyjaśniają to, co obserwowalne. Jak więc ustala się prawa, gdy np. brakuje pewnych danych i jak buduje się teorie naukowe?
Poincaré w Nauce i metodzie sformułował hipotezę o charakterze psychologicznym, dotyczącą mechanizmów rozwiązywania tego typu problemów. Rozważania jego dotyczyły wprawdzie twórczości matematycznej, ale łatwo je przenieść na teren nauk przyrodniczych, tym bardziej, że zgadzają się one z uwagami, jakie na temat pracy fizyków poczynił w Nauce i hipotezie. Proces twórczy rozpoczyna się od świadomego gromadzenia dostępnego materiału i sformułowania problemu. Jest faktem, pisze Poincaré na podstawie własnych wspomnień, że pierwsze, świadome próby rozwiązania problemu są zwykle daremne. Potem następuje okres pracy podświadomej, odbywającej się często podczas snu lub w okresie, gdy uczony zajęty jest innymi sprawami. Aż następuje olśnienie: badacz nagle zdaje sobie sprawę, że zna hipotetyczne rozwiązanie. Następnie – już świadomie – je sprawdza. Jeśli okaże się ono (prawdopodobnie) trafne, to wynik można opublikować; jeśli nie, trzeba próbować dalej. Ale skąd wzięło się samo rozwiązanie? Hipoteza Poincarégo głosi, że w trakcie wstępnego, świadomego okresu pracy, elementy dostępnej uczonemu wiedzy zostają w jego umyśle niejako wprawione w ruch, po czym, już w podświadomości, tworzą w sposób najzupełniej przypadkowy wszelkie możliwe kombinacje. Tych jest zazwyczaj ogromnie wiele i gdyby nie istniał jakiś mechanizm – podświadomej – selekcji powstających zestawień, do niczego by cały ten proces doprowadzić nie mógł. Fakt, iż dokonujemy odkryć teoretycznych, świadczy o tym, że – choć nie wszyscy w równym stopniu – jesteśmy w stanie takiej selekcji dokonywać. Czynimy to dzięki poczuciu piękna i harmonii: podobnie jak zdolni muzycy w sekwencji generowanych przypadkowo dźwięków wychwytują piękne motywy, genialni uczeni są w stanie wychwycić te zestawienia, które – dzięki swej prostocie – rokują nadzieję na to, że okażą się trafne. Ponieważ dzieje się to prawie całkowicie w podświadomości, uczony nie jest w stanie potem powiedzieć, na czym proces odkrycia teorii polegał. Ale też tylko ci, których los wyposażył w poczucie piękna i harmonii rozwinięte w wysokim stopniu, mają szansę zostać twórcami, wydobywać z morza powstających w podświadomości kombinacji te, które mogą okazać się teoretycznie płodne. (O trafności koncepcji Poincarégo może świadczyć znany fakt, że wybitni matematycy i fizycy teoretycy mają często duże zdolności muzyczne).
Mamy zatem dwie metody odkrywania praw: niektóre z nich uzyskujemy uogólniając wyniki doświadczeń do postaci prostej zależności, inne stawiając hipotezy będące owocem podświadomych procesów psychicznych selekcjonowanych przez „zmysł harmonii”.
Jeśli wydobędziemy z prostych – być może – faktów prostą – być może – zależność, to należy sprawdzić, czy można jej nadać miano prawa. Prawem jest formuła stosowalna do wielu różnych faktów, a nie tylko do tych, na podstawie których ją sformułowano. Stopień ogólności praw bywa różny. Tak np. prawa Galileusza z dobrym przybliżeniem stosowały się do opisów ruchów ciał w pobliżu powierzchni Ziemi; prawa mechaniki Newtona natomiast z przybliżeniem jeszcze lepszym stosowały się do opisów ruchów planet, ich księżyców, komet, a również ruchów pocisków, wahadeł, przypływów i odpływów mórz i bezliku innych faktów. W ten sposób Newton odsłonił harmonię i piękno ukryte pod powierzchnią zjawisk, co do których wcześniej nawet nie przypuszczano, że są ze sobą spokrewnione. Sukces naukowca jest tym większy, im bardziej odkryte przez niego prawa są ogólne. Ale oczywiście z chwilą odkrycia prostej zależności nie wiadomo, czy występuje ona gdziekolwiek poza faktami, z których ją wydobyto. Nie wiadomo nawet, czy obowiązuje ona dla tych właśnie faktów, a nie jest tylko sprawą przypadku, że punkty doświadczalne ułożyły się na pewnej krzywej; gdybyśmy zaś dokonali większej liczby i dokładniejszych pomiarów, prostą funkcją połączyć już by się tych punktów nie udało. Kolejnym krokiem po sformułowaniu domniemanego prawa jest zatem poddanie go doświadczalnemu sprawdzeniu.
Sprawdzać możemy prawo, powtarzając pierwotne doświadczenia i zagęszczając punkty pomiarowe lub zwiększając precyzję pomiarów. Ciekawszym będzie sprawdzanie prawa poza zakresem pomiarów wyjściowych. Boyle zagęszczał powietrze w zakresie od 1 (równy poziom rtęci w obu ramionach) do 3 atmosfer, pracujący niezależnie w 12 lat później Mariotte, posługując się dodatkowo rurką odwróconą, zmniejszał też ciśnienie do 0,5 atmosfery. W tym zakresie ciśnień otrzymywano, w granicach błędów doświadczalnych, zależność V = c / p. Należało teraz obmyślić doświadczenia umożliwiające pomiary dla ciśnień większych od 3 atmosfer i mniejszych od 0,5 atmosfery. Następnie należałoby przejść do faktów odmiennych rodzajów, na przykład zastępując powietrze innymi gazami, robiąc pomiary dla gazów w różnych temperaturach itp. W przypadku zależności w rodzaju praw mechaniki Newtona mamy takich możliwych rodzajów faktów niezliczenie wiele. Sprawdzanie prawa, polegające na powiększaniu zakresu i precyzji doświadczeń, a także na rozszerzaniu badań na nowe typy zjawisk, trwać może bez końca i niewątpliwie, twierdzi Poincaré, zdołamy w końcu wykazać, że prawo jest tylko przybliżone lub ma ograniczony zakres stosowalności (tak jak prawo Boyle’a–Mariotte’a przestaje obowiązywać dla bardzo wysokich ciśnień lub bardzo niskich temperatur). W każdym razie nie jesteśmy w stanie dowieść prawdziwości praw na podstawie wyników doświadczeń: wynik każdego następnego doświadczenia, niezależnie od historii wcześniejszych badań, może okazać się niezgodny z opartymi na posiadanych teoriach przewidywaniami.
3. Zasady i prawa doświadczalne
Jednak – i tu tkwi sedno całej sprawy – nie musimy czekać na ewentualne załamanie się prawa, pozostając w stanie permanentnego wątpienia: możemy w pewnym momencie przerwać sprawdzanie i podnieść prawo do godności zasady, czyli traktować je odtąd jako niewzruszenie prawdziwe. Zasady, w które – na mocy wspólnotowej decyzji – przestajemy wątpić, służą jako podstawa dalszych badań.
Przyroda, jak powiedziano, sugeruje nam prawa. W pewnym sensie sugeruje też zasady, tymi ostatnimi mogą bowiem stać się tylko te prawa, które przeszły pomyślnie przez szereg sprawdzianów, a nie od nas zależy, czy rzeczywistość okaże się zgodna z naszymi na jej temat poglądami. Jednak przyroda zasad nam nie narzuca: to my postanawiamy, by w pewnej chwili przerwać sprawdzanie i odtąd traktować dane prawo jako z pewnością prawdziwe. A potem rzutujemy zasady na przyrodę.
Zasada bezwładności (czyli pierwsze prawo dynamiki Newtona) została niewątpliwie zasugerowana przez pewne proste fakty, takie jak ruch kul toczących się po poziomych płaszczyznach. (Stało się to w ciągu pierwszej połowy XVII w. Trzeba jednak pamiętać o tym, że inteligentni ludzie obserwowali toczące się kulki przez całe stulecia, a przecież im zasady bezwładności to nie zasugerowało). Potem wokół tego prawa ukształtowany został system mechaniki Newtona, który dostarczył ogromnej liczby wyjaśnień i przewidywań bardzo rozmaitych zjawisk. Czas jakiś prawo bezwładności budziło wśród fizyków sprzeciwy, ale przed 1700 r. oponenci znikli, a ono zostało przeobrażone w niepodważalną zasadę. A przecież zasada ta, wzięta w izolacji, przedstawia fakty, jakie nie istnieją! Żadne znane nam ciało nie porusza się przez dłuższy czas ruchem jednostajnym po linii prostej. To jednak nie przeszkadza nam wierzyć w niepodważalność zasady bezwładności: po prostu ilekroć obserwujemy, że dane ciało zmienia prędkość lub kierunek ruchu, tylekroć postulujemy, iż działa na nie jakaś niezrównoważona siła. Jeszcze jaśniej pojmiemy, o co chodzi, gdy porównamy sytuacje problemowe, wobec jakich stali zwolennicy fizyki Arystotelesa i Newtona. Ci pierwsi do godności zasady podnieśli prawo mówiące, że wszelkie nienaturalne ruchy, np. ruchy ciał nieożywionych w kierunku poziomym, wymagają działania siły poruszającej; dlatego też widząc, że pchnięta po gładkiej powierzchni kula toczy się nadal po utracie kontaktu z pierwotnym sprawcą ruchu, postulowali istnienie sił ruch ten podtrzymujących (takich jak siła wywierana z zewnątrz przez powietrze lub od wewnątrz jako nabyty przez ciało impetus). Ci drudzy do godności zasady podnieśli prawo bezwładności i dopóki kula toczyła się ruchem niemal jednostajnym, niczego więcej nie potrzebowali wyjaśniać; musieli natomiast postulować istnienie sił (takich jak siły tarcia i oporu powietrza), aby wytłumaczyć, dlaczego ruch w końcu ustaje – co zupełnie nie martwiło arystotelików. Jedni i drudzy sił żadnych nie widzieli, ale je postulowali, albowiem wymagały tego, w obliczu faktów, przyjęte zasady.
Przeobrażając prawo w zasadę dokonujemy, co istotne, swoistego zabiegu idealizacyjnego, analogicznego do tego, jaki czynimy w geometrii, gdy w miejsce linii rysowanych na papierze, zawsze trochę krzywych, grubawych i o skończonej długości przedstawiamy sobie linię doskonale prostą, nieskończenie cienką i nie mającą końców. W naukach empirycznych też nie uzyskujemy dokładnej zgodności praw z wynikami doświadczeń, nasze pomiary obarczone są przecież błędami, a przebieg badanych zjawisk zawsze zakłóca, w mniejszym lub większym stopniu, wiele czynników, które pomijamy jako mniej istotne lub nie zdajemy sobie sprawy z ich występowania. Zasady abstrahują od złożoności zjawisk i mówią o tym, co by było gdyby. Mówią np. o punktach materialnych, o procesach niezakłócanych przez siły tarcia, o przewodach nierozgrzewających się pod wpływem płynącego przez nie prądu, o ciałach stałych doskonale sztywnych itp.
Zasady funkcjonują jako zamaskowane definicje występujących w nich pojęć (tę ideę przejął Poincaré od Milhauda). Zgodnie z zasadami mechaniki klasycznej ciało, na które nie działałaby żadna siła, poruszałoby się ruchem jednostajnym po linii prostej – ale tylko w inercjalnym układzie odniesienia. A co to jest inercjalny układ odniesienia? Nie jest to coś, na co dałoby się wskazać niezależnie od zasady bezwładności. Układ inercjalny jest to właśnie taki układ odniesienia – i to jest jego cecha definicyjna – w którym ciało, na które nie działałaby żadna siła, poruszałoby się ruchem jednostajnym po linii prostej. Podobnie drugie prawo dynamiki Newtona, a = F / m (przyspieszenie, jakiego doznaje ciało, jest proporcjonalne do działającej siły, a odwrotnie proporcjonalne do jego masy), definiuje niejawnie, łącznie z pozostałymi prawami mechaniki, pojęcia siły i masy.
Zasady dynamiki ukazują nam się przede wszystkim jako prawdy doświadczalne; zostaliśmy jednak zmuszeni do posługiwania się nimi jako definicjami. Właśnie z definicji zaczerpnęliśmy to, że siła jest równa iloczynowi masy i przyspieszenia; oto zasada która od tej pory znajduje się poza zasięgiem jakiegokolwiek późniejszego doświadczenia. Tak samo, na podstawie definicji, akcja jest równa reakcji (1902, § VI).
System teoretyczny nie traci w wyniku takich zabiegów idealizacyjnych kontaktu z doświadczeniem. Podnosząc bowiem prawo do godności zasady, rozbija się je na zasadę i na prawo doświadczalne, które niejako zapełnia lukę między zasadą a faktami. Ono też podlega rewizji, jeśli fakty okazują się niezgodne z przewidywaniami. Rozważmy prosty przykład. Galileusz sformułował zasadę głoszącą, że gdyby na spadające swobodnie ciała nie działał opór powietrza, to poruszałyby się one ruchami jednostajnie przyspieszonymi, a wartość przyspieszenia byłaby identyczna dla nich wszystkich. Każde jednak ciało, jakie można było wówczas obserwować, spadało w stawiającym opór powietrzu lub w różnego rodzaju cieczach. Dlatego Galileusz sformułował dodatkowo cały szereg praw doświadczalnych, mówiących np., że w przypadku kul ołowianych lub żelaznych spadających ze stosunkowo niewielkimi prędkościami opór powietrza można „z dobrym przybliżeniem” pominąć, a znów dla innych przypadków starał się wpływ oporu w ogólny sposób oszacować.
Kiedy jakieś prawo zostaje w sposób dostateczny potwierdzone przez doświadczenie, możemy przyjąć dwie postawy: albo pozostawić to prawo wśród rywalizujących ze sobą praw; wtedy będzie ono poddawane nieustannej rewizji, która bez żadnej wątpliwości skończy się wykazaniem, że jest ono tylko przybliżone; albo też można je podnieść do godności zasady, stosując takie konwencje, żeby twierdzenie było na pewno prawdziwe. W tym przypadku postępuje się zawsze w ten sam sposób. Pierwotne prawo wyraża relację między dwoma surowymi faktami A i B; pomiędzy te dwa surowe fakty wprowadzamy pośrednie pojęcie oderwane C, mniej lub bardziej fikcyjne (…). A wtedy mamy relację między A i C, którą możemy uważać za ścisłą i która jest zasadą; i druga pomiędzy C i B, która pozostaje prawem podlegającym rewizji. (1905, § X,4).
Wyprowadzamy zatem wnioski doświadczalne nie z samych zasad, ale z koniunkcji zasad i praw doświadczalnych. A kiedy wniosek nie zgadza się z faktami, to na mocy decyzji metodologicznej uznajemy, że za niepowodzenie odpowiedzialne są prawa, a nie zasady. Przetłumaczmy wywody Poincarégo na język logiki, wybierając najprostszy z przypadków, gdy z koniunkcji jednej zasady Z i jednego prawa doświadczalnego P wynika zdanie O, opisujące wynik pewnego doświadczenia. Załóżmy, że wyniki doświadczeń zaprzeczyły O, mamy zatem
z Z i P wynika
logicznie O
O (na mocy wyników doświadczeń) jest fałszywe
----------------------------------------------------------------
Z jest fałszywe lub P jest fałszywe
Z punktu widzenia logiki fałszywość O dowodzi fałszywości zasady lub prawa. Jeśli jednak na mocy decyzji metodologicznej ustaliliśmy, że zasada jest prawdziwa (nie w sensie zgodności z rzeczywistością, ale dlatego, że my ją jako prawdziwą traktujemy) to mamy schemat obalania praw doświadczalnych:
z Z i P wynika
logicznie O
O (na mocy wyników
doświadczeń) jest fałszywe
Z (na mocy milczącej
umowy między uczonymi) jest prawdziwe
-----------------------------------------------------------------------------------
P jest fałszywe
Rozważmy jeszcze jeden przykład. Analizując w oparciu o równanie F = ma ruchy planet, Newton wyprowadził w latach 1665–1666 prawo grawitacji, zgodnie z którym Słońce i planety działają na siebie siłami proporcjonalnymi do iloczynu ich mas, a odwrotnie proporcjonalnymi do kwadratu odległości między nimi. Prawo to zastosowano następnie do analizy wielu innych zjawisk, takich jak ruchy pocisków czy wahadeł w pobliżu powierzchni Ziemi, przypływy i odpływy mórz – i we wszystkich tych przypadkach zostało ono potwierdzone. Podniesiono je zatem w ciągu XVIII w. do godności zasady. Gdyby pod koniec XVII w. dostrzeżono przez teleskop jakiś inny układ planetarny (załóżmy, że było to wówczas możliwe), w którym planety nie poruszałyby się zgodnie z prawami mechaniki i prawem grawitacji, to jest wysoce prawdopodobne, iż prawo grawitacji uznano by za doświadczalnie obalone. Gdyby układ taki dostrzeżono pod koniec XVIII w., sytuacja byłaby inna. Do tego czasu prawo grawitacji rozpadło się na zasadę mówiącą, że każde dwa ciała przyciągają się wzajemnie siłą o postaci F = Gm1m2/r2, oraz na prawo doświadczalne, zgodnie z którym grawitacja jest jedyną siłą działającą na planety. Uznano by w tej sytuacji zapewne, że kłopotliwe obserwacje obalają wspomniane prawo doświadczalne, zasadę pozostawiając nietkniętą. Rozważania te wyjaśniają, dlaczego zasady mechaniki, choć sprawdzone z pewnym przybliżeniem i w ograniczonym zakresie, uważane są za absolutnie prawdziwe i stosowalne do całości wszechświata.
Jeśli postulaty te mają wartość
uogólnienia i pewność brakująca prawom doświadczalnym, z których zostały one
wysnute, to dlatego, że ostatecznie sprowadzają się do zwykłej konwencji, co
mamy prawo zrobić, ponieważ z góry jesteśmy pewni, że żadne doświadczenie jej
nie zaprzeczy.
Konwencja ta nie jest jednak wcale
dowolna; nie jest ona wynikiem naszego kaprysu; przyjmujemy ją, gdyż pewne
doświadczenia wykazały nam, że byłaby wygodna.
Wyjaśnia się w ten sposób, jak na
podstawie doświadczenia mogły powstawać zasady mechaniki i dlaczego, pomimo to,
nie będzie ono mogło ich obalić.
Zróbmy porównanie z geometrią. Podstawowe
twierdzenia geometrii, na przykład postulat Euklidesa, także są tylko
konwencjami i jest równie nierozsądne dociekanie, czy są one prawdziwe, jak
pytanie, czy system metryczny jest prawdziwy. (…)
Zasady są ukrytymi konwencjami i
definicjami. Wysnute są one jednak z praw doświadczalnych, prawa zaś te, że tak
powiem, przedzierzgnęły się w zasady, którym nasz umysł przypisuje wartość
absolutną (1902,
§
XVIII, Wnioski).
4. Czy wyniki doświadczeń mogą zdetronizować zasady?
Przyjrzyjmy się dwu słynnym przypadkom z dziejów fizyki i astronomii, których Poincaré nie omawia, ale które wiodą wprost do wielkiego pytania o wybór zasad i rolę w tym wyników doświadczeń. W latach czterdziestych XIX w. stało się jasne, że odkryta pół wieku wcześniej planeta Uran nie porusza się dokładnie tak, jak zgodnie z prawami mechaniki, prawem grawitacji i ówczesną wiedzą o Układzie Słonecznym poruszać się powinna. Zgodnie z zawartymi wcześniej przez społeczność uczonych umowami, pracujący niezależnie John Adams i Urbain Le Verrier trwali przy przekształconych w zasady trzech prawach dynamiki i prawie grawitacji. Trwali również przy prawie doświadczalnym głoszącym, iż grawitacja jest jedyną siłą działającą na planety. Przyczyn rozbieżności szukali w założeniu określającym liczbę ciał działających grawitacyjnie na Urana. Zaczęli od rozważenia możliwości najprostszej, czyli od hipotezy o istnieniu jednej nieznanej planety; po czym, dopasowując odpowiednie wielkości do danych z tablic astronomicznych, zdołali określić jej masę i trajektorię. Johann Galle, poinformowany o wynikach obliczeń Le Verriera, dostrzegł nową planetę w miejscu oddalonym o ok. 1º od położenia przewidzianego.
Analogicznym rozumowaniem próbował posłużyć się w latach pięćdziesiątych XIX w. Le Verrier, gdy stwierdzono, że ruch planety Merkury również przebiega nieco inaczej niż to wynikało z zasad mechaniki, zasady grawitacji, szeregu praw doświadczalnych, a wreszcie założeń określających liczbę, masy i trajektorie ciał w znaczący sposób oddziałujących na Merkurego grawitacyjnie. Postulowanej nowej planety jednak nie odkryto. Zawiodły również hipotezy o niesymetrycznym rozkładzie masy Słońca, o istnieniu niewidzialnego strumienia pyłu kosmicznego itd. Wreszcie fizycy podjęli próby modyfikacji prawa grawitacji (Tisserand 1872; Levy 1890); a zatem poczęto sprowadzać zasadę z powrotem do rangi prawa. Historia ta zakończyła się zastąpieniem mechaniki klasycznej przez ogólną teorię względności, którą Einstein ogłosił w 1916 r.
Powstaje w tym miejscu pytanie o kluczowym znaczeniu: „czy i w jakiej sytuacji można, lub należy, podjąć decyzję detronizującą zasady?”. Kiedy niezgodność z faktami świadczy już nie o fałszywości towarzyszących zasadom praw doświadczalnych, ale dostarcza racji przemawiających przeciw takiej czy innej zasadzie? Wokół tego pytania obracają się niemal wszystkie systemy metodologiczne omawiane w tej książce. Poincaré jasnej na nie odpowiedzi nie udzielił.
Trzeba, po pierwsze, pamiętać o tym, że sytuacje problemowe, z jakimi mamy do czynienia w praktyce naukowej, są niesłychanie bardziej skomplikowane niż by to sugerował powyższy schemat obalania praw doświadczalnych. Zdania opisujące fakty wynikają zwykle z koniunkcji ogromnej liczby przesłanek, z których część dotyczy bytów postulowanych przez teorie, a nieobserwowalnych. Mamy zatem bardzo wiele możliwości usunięcia niezgodności przewidywań teoretycznych i faktów. Możemy odrzucić jedną, dwie lub więcej przesłanek, możemy je zmodyfikować, możemy wreszcie zachować wszystkie przesłanki, a dodać jakieś nowe. Tego typu rozważania leżą u podstaw holistycznej filozofii nauki Pierre’a Duhema (La Théorie physique. Son objet et sa structure, 1906), który uważał w związku z tym, że w obliczu kłopotliwych faktów doświadczalnych zawsze, kosztem reszty systemu, możemy obronić dowolnie wybraną grupę twierdzeń. Ale choć logika, powiadał dalej Duhem, nie może zmusić nas do porzucenia danego prawa, to w pewnych sytuacjach może nas do tego skłonić zdrowy rozsądek, podpowiadający, które części teoretycznego systemu są odpowiedzialne za niepowodzenia.
Sama logika nie jest w stanie – w obliczu jakichkolwiek rezultatów doświadczeń – zmusić nas do odrzucenia wybranej zasady: zawsze możemy obstawać przy danym twierdzeniu, modyfikując inne części systemu teoretycznego. Tak więc (tego przykładu nie ma w pismach Poincarégo) inteligentni ludzie trwali aż do I połowy XVII w. przy zasadach fizyki Arystotelesa, wbrew oczywistym – z punktu widzenia ludzi wychowanych na fizyce nowożytnej – kontrświadectwom doświadczalnym, uzupełniając zasady Stagiryty m.in. o rozmaite wersje teorii impetusu. Podobnie (w tę historię Poincaré uwikłany był osobiście) na przełomie XIX i XX w. fizycy niemal jednomyślnie obstawali przy zasadach mechaniki klasycznej, wbrew piętrzącym się coraz bardziej trudnościom związanym ze wspomnianymi powyżej odkryciami doświadczalnymi. Trudności te próbowano usunąć, uzupełniając mechanikę m.in. o rozmaite wersje teorii eteru.
Można przyjąć stanowisko skrajne i twierdzić, że zawsze wolno nam uzgadniać wybrane zasady z wynikami doświadczeń za pomocą najrozmaitszych hipotez „ratunkowych”: metodologiczna decyzja, umowa zawarta (milcząco) między uczonymi, aby traktować pewne prawa jako niewzruszenie prawdziwe, raz na zawsze zabezpieczałaby je przed werdyktem doświadczenia. Poincaré takiego skrajnego poglądu nie przyjął. Przyznawał, że żadnej hipotezy nie można poddać próbie decydującej, ale w Nauce i hipotezie pisał, iż w pewnych sytuacjach, gdy zasada „przestaje być płodna, doświadczenie, nie zaprzeczając jej bezpośrednio, potępi ją jednak”. Byłaby to jakaś odpowiedź na pytanie, w jakich sytuacjach należy odrzucać same zasady, gdyby Poincaré wyjaśnił, co znaczą wyrażenia „przestaje być płodna” i „potępi ją”. Niestety, pozostawił na ten temat jedynie garść niejasnych sugestii. (Omówioną w rozdziale 6 metodologię Lakatosa można traktować jako pewną propozycję eksplikacji tych dwóch wyrażeń, skodyfikowania intuicji, do jakich Poincaré się odwoływał, choć wysłowić ich nie potrafił).
Michael Polanyi w Personal Knowledge. Towards a Post-Critical Philosophy (1958) twierdził, że te intuicje, które kierują pracą uczonego, są z istoty niewyrażalne. W wyniku złożonego procesu edukacyjnego, a potem praktyki prowadzonej pod nadzorem mistrzów, nabywamy umiejętności konieczne do uprawiania nauki podobnie jak opanowujemy rodzimy język: uczymy się na przykładach, naśladując innych i słuchając ich uwag, a nie w wyniku opanowania ogólnych reguł. Podobnie nie istnieje zbiór reguł, który decydowałby o tym, że dany utwór muzyczny jest wielkim dziełem sztuki, ale słyszą to ci, którzy przeszli przez złożony proces muzycznej edukacji. A choć oceny, jakie ferują, jawią się im jako oczywiste, to nie potrafią powiedzieć profanom, dlaczego tak jest. Jest tak też w przypadku nauki: wybitni naukowcy wyczuwają np., w jaki sposób przygotować eksperyment i jak opisać jego wyniki, które rezultaty doświadczeń są ważne, jak rozwiązywać naukowe problemy lub która teoria jest dobra, a która nie. Ale choć we własnym gronie na ogół w takich sprawach się zgadzają, to nie są w stanie wyjaśnić laikom, na jakiej podstawie takich ocen dokonują. Nie da się słownie wyczerpująco wyjaśnić, na czym polega uprawianie nauki: „Wiemy więcej, niż jesteśmy w stanie powiedzieć”.
Czy można tego rodzaju pogląd, określany przez Lakatosa mianem „elitaryzmu”, przypisać Poincarému? Sprowadzałby się on w tym przypadku do twierdzenia, że dobry naukowiec czuje, kiedy doświadczenie „potępia” teorię, a ona „przestaje być płodna”, choć nie potrafi tego wyrazić słowami. Do takiej interpretacji skłania nacisk, jaki autor Nauki i hipotezy kładł na rolę w praktyce badawczej „poczucia piękna i harmonii”. Naukowiec rozpoznaje, kiedy teoria przestaje być prosta, a tym samym piękna, ale nie może tego stwierdzić, ani nawet zrozumieć, człowiek w „zmysł harmonii” niewyposażony.
Spróbujmy prześledzić proces utraty prostoty na przykładzie nawiązującym po części do analiz Poincarégo. Na przełomie XVI i XVII w. współzawodniczyły ze sobą dwie hipotezy, z których jedna, ptolemeuszowa, w środku świata umieszczała Ziemię, a druga, kopernikańska, Słońce. Można by – odwołując się do XX-wiecznej teorii względności – twierdzić, że obie hipotezy były równoważne, opisywały jedynie ruchy ciał niebieskich w różnych układach odniesienia (które jedna i druga błędnie absolutyzowały). Spór między nimi był empirycznie nierozstrzygalny (na co zwracali uwagę zarówno Osiander, jak i Bellarmino), bo przecież nie widzimy środka świata, sfer planetarnych, epicykli, deferentów i ekwantów – czego istnienie obie teorie postulowały. Widzimy tylko na niebie jasne punkty – zwane „gwiazdami błądzącymi”, czyli planetami – zmieniające swoje położenia na tle innych jasnych punktów względem siebie nieruchomych, czyli „gwiazd stałych”. Obie hipotezy można było bez końca dopasowywać, np. mnożąc epicykle na epicyklach, do wyników obserwacji astronomicznych. Dalszy rozwój wydarzeń sprawił jednak, że system heliocentryczny stawał się coraz bardziej „prosty i harmonijny”, podczas gdy system geocentryczny, gdyby nadal broniono go po, powiedzmy, 1700 r., traciłby prostotę i harmonię coraz bardziej i bardziej. Tylko hipoteza heliocentryczna mogła doprowadzić Keplera do odkrycia matematycznych harmonii w ruchach planetarnych. Zjawiska aberracji światła gwiazd (zaobserwowanej w 1728 r.) i paralaksy gwiezdnej (stwierdzonej w 1838 r.) wynikały (przy pewnych obiegowych wówczas założeniach) wprost z wyjściowego modelu Kopernika, podczas gdy w ramach teorii geocentrycznej trzeba by było wyjaśniać je za pomocą wysoce dziwacznych hipotez dodatkowych. A wreszcie umieszczenie Słońca w centrum układu planetarnego stanowiło konieczny warunek odkrycia prawa grawitacji, co doprowadziło do powstania zdumiewającej swą prostotą i harmonią mechaniki Newtona. W tej nowej teorii Słońce nie znajdowało się już w środku świata, ale wraz z planetami obracało się, gdzieś w przestrzeni, wokół wspólnego środka masy. „Środek masy” nie jest, oczywiście, pojęciem doświadczalnym i nie sposób – odwołując się do „czystych” doświadczeń – stwierdzić, czy to ostatnie twierdzenie jest prawdziwe. Środek masy jest tam, gdzie na to wskazuje analiza ruchów ciał dokonana w oparciu o prawa mechaniki. Naukowcy czują natomiast, że system jako całość jest prosty, harmonijny, piękny. Więcej nie da się tu powiedzieć.
Poincaré równie często, co o harmonii i prostocie, pisał jednak o wygodzie: przyjmujemy daną konwencję, „gdyż pewne doświadczenia wykazały nam, że byłaby wygodna”. Nie jest jasne, co rozumiał przez „wygodę”, choć tu i ówdzie wiązał ją właśnie z prostotą. Nie sądzę, aby udało się definitywnie rozwikłać związane z tym zagadki interpretacyjne. Zamiast tego przyjmijmy, jako hipotezę roboczą, twierdzenie, iż Poincaré był elitarystą i przyjrzyjmy się, w jaki sposób, kierując się swym nieanalizowalnym zmysłem harmonii, oceniał sytuację, w jakiej znalazła się fizyka na początku XX w.
Zacznijmy od sytuacji w geometrii. Twierdzenia geometrii euklidesowej, o czym była mowa na początku tego rozdziału, pierwotnie zostały zasugerowane przez doświadczenia związane z rozchodzeniem się światła i ruchami ciał stałych. Ponieważ okazało się, iż wygodnie jest za pomocą euklidesowej geometrii opisywać świat, podniesiono jej twierdzenia do rangi zasad, traktując je odtąd jako prawdy niewzruszone, a stosując faktycznie jako definicje. W roli zasad odnosiły się do faktów nie bezpośrednio, ale dopiero po dodaniu odpowiednich praw doświadczalnych, mówiących np., że pewne przedmioty z drewna czy z metalu nieodkształcane siłą i w stałej temperaturze można „z dobrym przybliżeniem” traktować jak ciała sztywne i że światło w ośrodkach optycznie jednorodnych rozchodzi się po liniach prostych. (A co to jest ośrodek optycznie jednorodny? Jest to, rzecz jasna, ośrodek, w którym światło rozchodzi się po liniach prostych. Powstające tu błędne koło nie jest rezultatem pojęciowego zamętu czy niedostatków systemu, ale należy do istoty ludzkiej wiedzy). Brak systemów alternatywnych do połowy XIX w. przyczynił się do powstania przesądu, jakoby twierdzenia geometrii Euklidesa były prawdami koniecznymi. Pojawienie się geometrii Łobaczewskiego i Riemanna obaliło ten pogląd. Czy należy w tak zmienionej sytuacji rozważyć zmianę systemu geometrycznego stosowanego w fizyce? Poincaré twierdził, że nie. Podawał dwa powody, dla których powinniśmy, spośród trzech dostępnych systemów geometrii, wybrać właśnie euklidesowy. 1) Geometria Euklidesa jest najprostsza z matematycznego punktu widzenia – moglibyśmy, gdybyśmy chcieli, opisywać świat za pomocą innych geometrii, stosując inne prawa doświadczalne, ale opisy byłyby mniej wygodne (tu sens jest jasny: obliczenia byłyby trudniejsze). 2) Geometria Euklidesa dobrze odpowiada własnościom ciał makroskopowych z naszego bezpośredniego otoczenia. A co by było, gdyby proponowane przez Gaussa pomiary kątów wielkich trójkątów dały wynik wyraźnie różny od 180°? Wtedy, upierał się Poincaré, należałoby modyfikować prawa fizyki towarzyszące stosowaniu geometrii do opisów kształtów, położeń i ruchów ciał tak, aby ratować aksjomaty Euklidesa przed obaleniem przez wyniki doświadczeń. Na mocy zalecanej przez niego decyzji doświadczenie nie tylko nie mogłoby obalić euklidesowej geometrii, ale nie byłoby nawet w stanie jej „potępić”.
Nie zajmował równie skrajnego stanowiska w odniesieniu do jakiejkolwiek teorii fizycznej. Tę różnicę należy chyba tłumaczyć faktem, iż, jego zdaniem, między geometrią a fizyką zachodzi ważna różnica: doświadczenia prowadzące nas do przyjęcia, jako pięknych i wygodnych, konwencji geometrycznych są doświadczeniami nie z zakresu geometrii samej, ale z zakresu mechaniki i optyki, podczas gdy konwencje teorii fizycznych przyjmujemy na podstawie doświadczeń z tego właśnie zakresu faktów, do którego dana teoria się odnosi. Zasady geometrii są przeto odleglejsze od doświadczenia niż zasady np. mechaniki czy elektrodynamiki.
W książce Wartość nauki Poincaré analizował sytuację problemową, w jakiej znalazła się fizyka na przełomie wieków XIX i XX. Dopuszczał możliwość, że tarapaty, w jakie popadła mechanika klasyczna w związku ze wspomnianymi anomalnymi wynikami doświadczeń, doprowadzą do tego, iż zostanie ona wyparta przez nową mechanikę, w której masa bezwładna będzie rosnąć z szybkością, a prędkość światła stanie się nieprzekraczalna. Ale jest też możliwe, podkreślał, że zasady fizyki klasycznej wyjdą z tych tarapatów zwycięsko – i sam zaangażował się w ich obronę. Pisząc wspomniany powyżej artykuł o dynamice elektronu (1905), zakładał – zgodnie z poglądem wówczas obiegowym – istnienie eteru, którego ukryte własności miały wyjaśniać zaskakujące wyniki doświadczeń związanych z wpływem ruchu układów na przebieg odbywających się w nich zjawisk elektromagnetycznych. Własności te należało odgadnąć. Poincaré, podobnie jak inni fizycy, mimo uporczywych wysiłków odgadnąć ich nie zdołał – a jednak do końca uznawał mechanikę klasyczną za fundament fizyki. Choć równania, które podał w 1905 r. były identyczne z podanymi przez Einsteina, to inaczej je interpretował – i dlatego nie uważa się go dziś za współtwórcę szczególnej teorii względności.
Przewidywał natomiast, że w bliskiej przyszłości odrzucona zostanie zasada zachowania energii. Sformułowano ją w połowie XIX w. w wyniku długotrwałych badań nad przekształcaniem się energii mechanicznej w ciepło i na odwrót. Lista postulowanych rodzajów energii ulegała, wraz z postępami badań, rozszerzeniu. Mówiono m.in. o energii kinetycznej, potencjalnej, chemicznej, o energii przekazywanej w procesach wymiany ciepła itd. Przez cały ten czas zasada zachowania energii była niezwykle płodna, pozwalała w licznych przypadkach przewidzieć, ile i jakiej energii wydzieli się w danym procesie. Pod koniec XIX w. odkryto jednak rad, substancję wydzielającą, jak się wówczas wydawało, nieograniczoną ilość energii – która nie wiadomo, skąd się brała. Poincaré wspomniał o jednej z ówczesnych hipotez, zgodnie z którą rad przechwytuje jakieś promieniowanie, przez inne substancje przenikające bez oporu, a energię tego promieniowania zamienia w światło i ciepło. Hipoteza ta – choć tłumaczyła zagadkowe własności radu i uzgadniała zasadę zachowania energii z wynikami doświadczeń kalorymetrycznych – nie prowadziła jednak do dalszych przewidywań, a na dobrą sprawę otwierała pole dla niczym nieskrępowanych spekulacji. Właśnie w odniesieniu do sytuacji, w jakiej znalazła się u progu XX w. zasada zachowania energii, powtórzył Poincaré w Wartości nauki cytowane już stwierdzenie ze swojej pierwszej książki: „jeśli zasada przestanie być płodna, doświadczenie, nie zaprzeczając jej bezpośrednio, potępi ją jednak” (1905, § 9).
Dalszy rozwój fizyki nie potwierdził tych ocen. Po 1905 r. relatywistyczna teoria pola szybko wyparła mechanikę klasyczną, zaś po 1916 r. za podstawową teorię wszechświata powszechnie uznano ogólną teorię względności, w której metryczne własności czasoprzestrzeni zmieniają się w zależności od rozkładu mas w danym obszarze, a tylko przestrzeń pusta (jakiej w naszym świecie nie ma) byłaby euklidesowa. Natomiast zasada zachowania energii, wzbogacona o Einsteinowskie równanie E = mc2, wyszła za wspomnianych trudności zwycięsko i do dziś stanowi jeden z fundamentów fizyki. Naukę uprawia się jednak metodą prób i błędów i nikomu nie wolno czynić zarzutów z tej racji, że jego intuicyjne oceny z perspektywy przyszłego rozwoju wydarzeń okazały się chybione.
5. Czy i w jakim sensie nauka poznaje świat?
Konwencjonalista jest zagrożony popadnięciem w skrajności dwojakiego rodzaju. Pierwsza, metodologiczna, sprowadza się do twierdzenia, że skoro zawsze można bronić teorii przed obaleniem przez wyniki doświadczeń, to decyzja o jej odrzuceniu w ogóle nie zależy od faktów doświadczalnych, a tym bardziej od jakichś praw myślenia (z wyjątkiem może pojęcia grupy i zasady indukcji matematycznej), ale wyłącznie od woli uczonych. Sugerowałoby to, że konwencjonalizm jest odmianą irracjonalizmu i taką opinię tu i ówdzie się spotyka, choć trudno, o czym za chwilę, taki pogląd przypisać Poincarému. Skrajność druga, filozoficzna, przechodzi od konstatacji, iż formy teoretyczne są produktami naszej wyobraźni twórczej, warunkującymi również sposoby, na jakie postrzegamy i opisujemy fakty, do tezy, że nauka nie poznaje świata, a jedynie tworzy pewne obrazy, które – biorąc własne wytwory za rzeczywistość – nazywamy światem. Podobnie jak kiedyś zdaliśmy sobie sprawę z tego, iż obrazy mityczne czy religijne nie są obrazami rzeczywistości, tak dziś konwencjonalistyczna filozofia wyzwala nas ze złudzenia polegającego na ontologizacji tych form poznawczych, które nazywamy teoriami naukowymi.
Tak zinterpretowany konwencjonalizm znosił, a w każdym razie znacznie zamazywał, epistemologiczną różnicę pomiędzy naukami przyrodniczymi a doktrynami religijnymi czy filozoficznymi. Pierre Duhem i Édouard Le Roy – obaj zaangażowani katolicy – rozwijali idee tej filozofii pobudzani nadzieją, że zlikwiduje ona, a przynajmniej znacznie osłabi, konflikt pomiędzy nauką a wiarą. Prace Duhema, bardzo wnikliwe z dzisiejszej perspektywy, Poincaré z niejasnych powodów ignorował, natomiast w ostatnich latach życia zwalczał radykalną wersję konwencjonalizmu, jaką głosił bergsonista Le Roy (polemiki ograniczały się do problemów filozofii nauki, bez nawiązywania do zagadnień filozofii religii czy poglądów Bergsona). Autor Wartości nauki przypisywał jednak Le Roy poglądy, których ten nigdy nie głosił, dlatego bezpieczniej będzie usunąć tu ów zwodniczy, polemiczny kontekst. Niezależnie od tamtych nieporozumień argumenty Poincarégo zachowały, z uwagi na dalszy rozwój filozofii nauki, wielką wagę. Zwalczaną przez siebie doktrynę Poincaré charakteryzuje następująco:
Nauka składa się wyłącznie z konwencji i jedynie tej okoliczności zawdzięcza ona swą pozorną pewność; fakty naukowe, a tym bardziej prawa są sztucznymi tworami uczonego; zatem nauka nie może niczego nauczyć nas o prawdzie, może nam tylko służyć jako reguła działania (1905, § 10.1).
Jeśli chcemy bronić tezy, że wiedza naukowa posiada wartość logiczną, to prowadzi to nas do pytania, czy prawdziwe lub fałszywe są teorie naukowe, czy tylko zdania o faktach. Poincaré twierdzi, iż na obu poziomach można odnaleźć zarówno elementy konwencjonalne, pozbawione wartości logicznej, jak i zdania prawdziwe lub fałszywe.
Jeśli chodzi o poziom teoretyczny, to jeszcze raz przypomina, że gdy w wyniku milczącej umowy między uczonymi podnosimy jakieś prawo do godności zasady, rozbijamy je na zasadę i prawo doświadczalne – a to drugie posiada wartość logiczną na mocy zgodności lub niezgodności z rzeczywistością. Tak więc jeśli np. prawo grawitacji przekształcimy w zasadę, pozbawiając je tym samym wartości logicznej (lub uznając za niepodważalnie prawdziwe, lecz nie na podstawie zgodności z rzeczywistością, tylko na mocy wspólnotowej decyzji), to prawdziwe lub fałszywe – w klasycznym tego słowa znaczeniu – stanie się twierdzenie, że grawitacja jest jedyną siłą działającą na planety. Nie jest też tak, aby, jak twierdził Le Roy, zdanie „fosfor topi się w 44 ºC” było po prostu definicją fosforu, bo kiedy, podkreśla Poincaré, takie zdanie wypowiadam, twierdzę, że każde ciało, mające takie i takie własności – pominąwszy w tej charakterystyce punkt topnienia – przejdzie w stan ciekły w temperaturze powyżej 44ºC. Będzie więc można odkryć, że to prawo jest fałszywe, a wtedy w pracach chemików przeczytamy zapewne „istnieją dwa ciała, brane dotąd za fosfor, a różniące się temperaturą topnienia”.
Jeśli chodzi o poziom obserwacji, to Poincaré podkreśla, iż nie ma mowy o tym, aby uczony stwarzał fakt: wszystko, co tworzy on w fakcie, sprowadza się do wyboru języka, w którym fakt zostaje opisany. Gdy już przyjmiemy pewien język, formułowane w nim zdania o faktach są prawdziwe lub fałszywe na mocy zgodności lub niezgodności z wynikami doświadczeń. To jest definicyjna cecha zdań o faktach (Poincaré, który notorycznie miesza fakty z ich opisami, pisze w tym kontekście nie „zdania”, a „fakty”): są to te zdania, których prawdziwość lub fałszywość da się stwierdzić – przy przyjętych konwencjach językowych – na podstawie wrażeń.
Można ten sam fakt opisać w różnych językach. Wyobraźmy sobie czterech ludzi obserwujących powtórkę omówionego powyżej eksperymentu Boyle’a. Proszeni o zdanie sprawy z tego, co widzą – zakładamy, że udzielono im wstępnych wyjaśnień przesądzających wybór faktu, tak iż żaden z nich nie zaskoczy nas opisem lotu muchy pod sufitem lub ubiorów laborantów – mówią po kolei:
– „w miarę jak
dolewamy rtęci do otwartego ramienia szklanej rurki poziom rtęci w ramieniu
zamkniętym podnosi się”;
– „w miarę jak wzrasta
różnica poziomów rtęci w obu ramionach rurki zmniejsza się objętość uwięzionej
porcji powietrza”;
– „w miarę wzrostu
ciśnienia objętość powietrza maleje”;
– „objętość powietrza
maleje proporcjonalnie do wzrostu ciśnienia”.
Słysząc takie relacje, pomyślimy zapewne, że pierwszy z obserwatorów jest ignorantem, drugi, a tym bardziej trzeci, posiadają pewną wiedzę z fizyki, zaś czwarty jest w tym zakresie specjalistą (aby stwierdzić odwrotną proporcjonalność ciśnienia do objętości trzeba m.in. obliczyć ciśnienie wskazywane przez różnicę poziomów rtęci i dodać do niego jedną atmosferę). Nas interesują w tej chwili języki, w jakich sformułowano te relacje. Pierwszy z obserwatorów użył języka potocznego, zrozumiałego dla ogółu ludzi mówiących po polsku. Czwarty posłużył się specjalistycznym językiem pewnych teorii fizycznych zrozumiałym dla nielicznych. Charakterystyczną cechą coraz bardziej specjalistycznych opisów jest to, że stosują się one do coraz większej liczby faktów jednostkowych: podczas gdy laik opisze zwykle jednostkowy fakt zachodzący tu i teraz, to w miarę rosnącego „unaukowienia” opisu zwracamy coraz bardziej uwagę na te cechy faktu, które są wspólne wielu faktom pod pewnym względem podobnym, a pomijamy inne. Naukowiec z naszego przykładu nie wspomina już, że rurka była zrobiona ze szkła, a użytą cieczą była rtęć, gdyż według przyjętych przez niego teorii są to cechy nieistotne dla przebiegu badanego zjawiska.
Na tej podstawie Poincaré odróżnia fakty naukowe i fakty surowe: te pierwsze to fakty opisane w języku teorii naukowej, drugie to fakty opisane w języku potocznym. (Co, zważywszy uwagi kończące poprzedni akapit, prowadzi do tezy, że na jeden fakt naukowy składa się wiele faktów surowych). Po czym stwierdza, iż uczeni nie tworzą faktów naukowych swobodnie, ale – po wyborze danego języka – narzucają im je fakty surowe. Te drugie stanowią, zdaniem autora Wartości nauki, fundament wszelkiej wiedzy. Zwolennicy różnych teorii odmiennie opiszą te same zjawiska, być może nie użyją ani jednego wspólnego słowa. Czy mamy na tej postawie powiedzieć – jak Kuhn, zob. rozdział 5 poniżej – że żyją oni w różnych światach i nie są w stanie się porozumieć? Poincaré broni zarówno możliwości porozumienia, jak i tego, iż uczeni ci jedynie różnie mówią o jednym i tym samym. Tym czymś wspólnym są właśnie fakty surowe. Możliwy jest mianowicie przekład wypowiedzi na temat stosunków między faktami naukowymi na wypowiedzi o stosunkach między samymi tylko faktami surowymi. Stosunki między faktami surowymi stanowią „niezmiennik powszechny”, to, o czym na rozmaite sposoby mówią różne teorie.
Umożliwia to nam ocenę, która z teorii jest lepsza pod względem poznawczym. Można z uporem twierdzić, że teoria Ptolemeusza nie została obalona przez wyniki obserwacji astronomicznych – przecież nadal można było mnożyć epicykle na epicyklach, tak aby dopasowywać konsekwencje teorii do danych z tablic astronomicznych. A zatem, twierdzą niektórzy, wybór pomiędzy systemami Ptolemeusza i Kopernika mógł być dokonany jedynie ze względów pozapoznawczych, tym bardziej, że faktycznie chodziło o wybór układu odniesienia do opisu ruchów ciał, a ten, jeśli nie wierzymy w istnienie absolutnych położeń, jest dowolny. Poincaré temu zaprzecza. Hipoteza kopernikańska nie tylko wyjaśniała obserwowane z Ziemi ruchy ciał niebieskich, ale – rozwinięta przez Galileusza i Newtona w system mechaniki – w ramach jednego systemu wyjaśniała też obrót płaszczyzny drgań wahadła Foucaulta, ruchy atmosfery ziemskiej i wód oceanicznych, spłaszczenie Ziemi i wiele innych faktów. Natomiast dobudowanie systemu mechaniki do teorii Ptolemeusza okazało się niemożliwe i wspomniane przed chwilą zjawiska pozostały z punktu widzenia zwolenników jego teorii niepowiązane ze zjawiskami ruchów ciał niebieskich. Nawet jeśli ograniczymy się do tego, co widać na niebie, to teoria Kopernika (już bez pomocy mechaniki) wiąże ze sobą w jednym systemie widoczne ruchy gwiazd i planet z jednej, a zjawiska aberracji i paralaksy gwiezdnej z drugiej strony, podczas gdy pozostają one niepowiązane z punktu widzenia teorii Ptolemeusza. O poznawczej wyższości teorii przesądza, zdaniem Poincarégo, to, że odkrywa ona stosunki wiążące większą liczbę bardziej różnorodnych faktów surowych (dziś określamy to mianem rosnącej unifikacji wiedzy).
Odkryte stosunki między faktami surowymi – prawa przyrody – stanowią trwały dorobek nauki: odnajdujemy je w różnych językowych przebraniach we wszystkich następnych teoriach. Wielu z tych, którzy głoszą, że nauka nie odkrywa prawdy, przez „prawdę” rozumieją coś, co dotyczyłoby istoty rzeczy. Jeśli zaakceptujemy podobny wymóg, to, stwierdza Poincaré, pozostanie nam przyznać, że sceptycy mają rację. Nauka jednak z samej swej natury nie odpowiada na pytania w rodzaju „czym jest grawitacja?”, „czym jest elektryczność?” itp. Nauka zapoznaje nas ze stosunkami między faktami surowymi – i tylko pod tym względem można mówić o prawdziwości jej twierdzeń. Chociaż te stosunki dają się pomyśleć jedynie jako ujmowane lub odczuwane przez jakiś umysł, to są obiektywne dlatego, że:
(…) to, co nazywamy rzeczywistością obiektywną, ostatecznie jest tym, co jest wspólne wielu istotom myślącym i co mogłoby być wspólne wszystkim; tą częścią wspólną (…) może być tylko harmonia wyrażona prawami matematycznymi. (1905, Wstęp).
W ten sposób twórca konwencjonalistycznej filozofii nauki, gdy ujrzał wnioski, jakie z jego pierwotnych twierdzeń wyprowadzili inni, próbował twierdzenia te osłabić i prawdę, jaką sam niegdyś wygnał z nauki, wprowadzić niejako tylnymi drzwiami z powrotem. Powstałych przy tym napięć i niekonsekwencji nie zdążył już usunąć, a jest wątpliwe, czy w ogóle ich usunięcie jest możliwe.
6. O wartości nauki
Na zakończenie podkreślmy jeszcze, że Poincaré nie zgadzał się ze zwolennikami poglądu, iż istotą nauki jest dostarczanie nam reguł działania, a zatem jej wartość leży w tym, że służy ona ludzkości przez swoje zastosowania techniczne. Wręcz przeciwnie, poznanie naukowe, jak z mocą podkreślał, stanowi wartość samo w sobie, a jeśli pobudza rozwój przemysłu, to tym lepiej, gdyż dzięki temu zyskujemy środki i psychologiczne pobudki do dalszego rozwijania nauki – dla niej samej.
Uczony nie bada przyrody dlatego, że jest to użyteczne; studiuje ją dlatego, że znajduje w tym przyjemność, a znajduje w tym przyjemność dlatego, że jest ona piękna. Gdyby nie była piękna, nie byłaby warta poznania, a życie nie byłoby warte, aby je przeżywać. (1908, § I,I).
Większość ludzi nie lubi myśleć, a kieruje nimi instynkt mający na względzie tylko doraźne potrzeby. Ludzie ci nie pozostawiliby po sobie więcej niż pszczoły czy mrówki, gdyby nie nieliczni szaleńcy, którzy często marli w biedzie, a nigdy nie myśląc o użyteczności tworzyli naukę i sztukę dla nich samych.
(…) jeśli Grecy pokonali barbarzyńców i jeśli Europa, dziedziczka myśli Greków, panuje nad światem, to dlatego, że dzicy lubili krzyczące barwy i hałaśliwe dźwięki bębna, które absorbowały tylko ich zmysły, podczas gdy Grecy kochali piękno intelektualne, ukryte pod pięknem widocznym i że to właśnie ono daje inteligencji pewność i siłę. (…) to bezinteresowne poszukiwanie prawdy dla własnego jej piękna jest zdrowe i może również uczynić człowieka lepszym (1908, § I,I).
Jeśli odrzucimy hasła „nauka dla nauki” i „sztuka dla sztuki”, jeśli uznamy, że obie powinny służyć potrzebom życiowym, to trudno będzie uniknąć wniosku, iż „cywilizacja ma na celu dostarczanie alkoholu tym, którzy lubią pić”. Tom Wartość nauki kończą w związku z tym słowa:
Jeśli cywilizacja ma wartość, to jedynie
dzięki nauce i sztuce. (…)
Co tylko nie jest myślą, jest czystą
nicością, gdyż jedynie myśl pomyśleć możemy, a wszystkie słowa, za pomocą
których mówimy o rzeczach, nie mogą wyrażać niczego prócz myśli; jeśli ktoś
powiada, że poza myślą jest jeszcze coś innego, wygłasza zatem twierdzenie,
które nie może mieć sensu.
A przecież – dziwna sprzeczność dla
wierzących w czas – historia geologiczna uczy nas, że życie jest tylko krótkim
epizodem między dwiema wiecznościami śmierci i że w samym tym epizodzie myśl
świadoma trwała i trwać będzie tylko krótką chwilę. Myśl jest tylko błyskiem na
tle długiej nocy.
Lecz
błysk ten właśnie jest wszystkim (1905, § XI,8).
Zbiory filozoficznych i popularnonaukowych tekstów Poincarégo
(1902) La science et l’hypothése, Paris. Wyd. pol. Nauka i hipoteza, tłum. L. Silberstein, J. Mortkowicz 1908.
(1905) La valeur de la science, Paris. Wyd. pol. Wartość nauki, tłum. L. Silberstein, J. Mortkowicz 1908.
(1908) Science et méthode, Paris. Wyd. pol. Nauka i metoda, tłum. L. Silberstein, J. Mortkowicz 1911.
(1913) Dernières pensées, Paris. Wyd. ang. Mathematics and Science: Last Essays, Dover Publications 1963. Fragm. Ostatnie myśli, tłum. I. Bukowski, w: I. Szumilewicz, Poincaré, Wiedza Powszechna 1978, s. 176–193.
Opracowania
Folina J. (1982) Poincaré and the Philosophy of Mathematics, Macmillan.
Giedymin J. (1982) Science and Convention: Essays on Henri Poincare’s Philosophy of Science and the Conventionalist Tradition, Pergamon.
Greffe J. L., Heinzmann, G., K. Lorenz, K. (red.) (1996) Henri Poincaré: Science et philosophie, Science and Philosophy, Wissenschaft und Philosophie, International Congress Nancy, France 1994, Blanchard.
Szlachcic K. (1992) Filozofia nauki francuskiego konwencjonalizmu, Wyd. Uniwersytetu Wrocławskiego.
Szumilewicz I. (1978) Poincaré, Wiedza Powszechna. (Na s. 194–278 nowe przekłady I. Bukowskiego fragmentów Nauki i hipotezy, Wartości nauki i Nauki i metody, przekłady te przedrukowane w: Filozofia nauki francuskiego konwencjonalizmu, K. Szlachcic (wyd.), Wyd. Uniwersytetu Wrocławskiego 1994, s. 53–97).
Literatura uzupełniająca
Ajdukiewicz K. (1934a) Sprache und Sinn, „Erkenntnis” 4, s. 100–138. Wyd. pol. Język i znaczenie, tłum. F. Zeidler, w: tenże, Język i poznanie, t. 1: Wybór pism z lat 1920–1939, WN PWN 1960, s. 145–174. (Ten i dwa następne teksty zawierają pewną odmianę konwencjonalizmu).
Ajdukiewicz K. (1934b) Das Weltbild und die Begriffsapparatur, „Erkenntnis” 4, s. 259–287. Wyd. pol. Obraz świata i aparatura pojęciowa, tłum. F. Zeidler, w: tenże, Język i poznanie, s. 175–195.
Ajdukiewicz K. (1935) Die Wissenschaftliche Weltperspektive, „Erkenntnis” 5, s. 22–30. Wyd. pol. Naukowa perspektywa świata, w: tenże, Język i poznanie, s. 215–221.
Dubik A. (1995) Tożsamość i opór. Główne kategorie epistemologii Emila Meyersona, Wyd. UMK.
Duhem P. (1894) Quelques réflexions au sujet de la physique expérimentale, „Revue des questions scientifique”, seria 2, 36, s. 179–229. Wyd. pol. Kilka refleksji na temat fizyki eksperymentalnej, tłum. M. Sakowska, w: Filozofia nauki francuskiego konwencjonalizmu, s. 17–52.
Duhem P. (1906) La théorie physique. Son objet, sa structure, Chevalier et Rivière. Fragm. w: K. Szlachcic, Filozofia nauk empirycznych Pierre’a Duhema, tłum. M. Sakowska, Wyd. Uniw. Wrocł. 2011, s. W36-W109. (Metodologiczne opus magnum Duhema, drukowane najpierw w czasopiśmie „Revue de philosophie” 1904–1905. Do wyd. 2, 1914, s. 273–311, Duhem dołączył artykuł Physique de croyant, z przesłaniem: skoro nauka nieuchronnie zawiera elementy konwencjonalne, to nie jest w stanie odkryć najgłębszych prawd o świecie, a zatem strażniczką metafizycznej prawdy jest, tak jak przed wiekami, teologia).
Duhem P. (1913–1959) La système du monde. Histoire des doctrines cosmologiques de Platon á Copernic, t. 1–10, A. Hermann. (Słynna historia astronomii).
Pierre’a Duhema filozofia nauki. Wybór tekstów, K. Szlachcic (wyd.), Wyd. Uniwersytetu Wrocławskiego 1991.
Le Roy E. (1899–1900) Science et philosophie, „Revue de métaphysique et de morale” 1899, 7, s. 375–425, 503–562, 706–731; 1900, 8, s. 37–72. Fragm. cz. 2, Nauka i filozofia, tłum. M. Zuber, w: Filozofia nauki francuskiego konwencjonalizmu, s. 99–124.
Le Roy E. (1906) Dogme et critique, Bloud. (Wyłożony w tej książce modernistyczny pogląd na dogmaty religijne jako na rozumowo niewytłumaczalne źródła dyrektyw moralnych, został potępiony przez Piusa X; inna książka E. Le Roy, Le problème de Dieu, L’Artisan du livre 1929, umieszczona została na Indeksie).
Martin R. N. D. (1991) Pierre Duhem: Philosophy and History in the Work of a Believing Physicist, Open Court.
Meyerson É. (1908) Identité et réalité, Alcan. Wyd. ang. Identity and Reality, Macmillan 1930. (Najważniejsza filozoficzna książka urodzonego w Lublinie, a mieszkającego we Francji chemika o legendarnej erudycji, w późniejszym okresie jednego z czołowych syjonistów).
Milhaud G. (1894) Essai sur les conditiones et les limites de la certitude logique.
Milhaud G. (1896) La Science Rationnelle, „Revue de Metaphysique et de Morale” 4, s. 280–302.