pitagor_matematycy

Wojciech Sady

Pierwsi pitagorejscy matematycy

z: Dzieje religii, filozofii i nauki: od Talesa z Miletu do Mahometa, Marek Derewiecki 2010

5. Pitagoras z Samos o wędrówce dusz i liczbach jako substancjach i zasadach
14. Filolaos z Krotonu o budowie świata
15. Pierwsi pitagorejscy matematycy

5. Pitagoras z Samos o wędrówce dusz i liczbach jako substancjach i zasadach

Gdzieś między 550 a 450 r. p.n.e. narodził się wielki program badawczy, który rozwijany był przez całą starożytność, a wskrzeszony w epoce renesansu w wiekach XVI i XVII w. odegrał kluczową rolę w procesie narodzin nauki nowożytnej. Jego inicjatorem miał być Pitagoras z Samos, ale nie da się określić wkładu, jaki wniósł on do filozofii noszącej jego imię. Kolejne bowiem pokolenia pitagorejczyków przypisywały mu własne osiągnięcia, a jednocześnie rosła legenda wyposażająca Pitagorasa w cechy nadprzyrodzone. Przyjrzyjmy się na początek temu wpół mitologicznemu obrazowi.

Pitagoras z Samos żył, według niepewnych szacunków, w latach od 570 r. do 480 p.n.e. Relacje o jego życiu są pełne sprzeczności, nie sposób w nich oddzielić faktów od legend. Jamblich twierdzi, że gdy miał lat dwadzieścia, odwiedził Talesa z Miletu, miał też słuchać wykładów Anaksymandra. Czas jakiś spędził w Egipcie, gdzie ponoć uzyskał święcenia kapłańskie. Po najeździe perskim na Egipt miał, jako jeniec, znaleźć się w Babilonie, gdzie przyswoił sobie tamtejszy dorobek w zakresie matematyki i muzyki. Wreszcie znalazł się w Krotonie, w południowej Italii, gdzie założył związek o charakterze religijno-filozoficzno-politycznym. Kandydatów przyjmowano na trzyletni okres próbny, po czym część kwalifikowano do pięcioletniego „okresu milczenia”. Pilnie obserwowano, czy przestrzegają przepisanych reguł postępowania, zachowują spokój pośród przeciwieństw losu, czynią postępy w nauce i potrafią dotrzymać tajemnicy. Wprowadzano ich tylko w pewne nauki, bez podawania rozumowych uzasadnień. Wykładów Pitagorasa słuchali nocą, mówcę dodatkowo skrywał welon. Oglądali go jedynie pełnoprawni członkowie, którzy po przekazaniu na rzecz związku całego mienia prowadzili wspólne życie, byli zapoznawani z pełnią doktryny i angażowani w badania. Aby dodatkowo chronić doktrynę przed niepowołanymi uszami, w rozmowach posługiwano się sentencjami zrozumiałymi jedynie dla wtajemniczonych, tzw. akusmata. Oto jedna z ich zachowanych list, ujawniająca coś z pitagorejskiego sposobu życia:

Był jeszcze inny, taki oto rodzaj symbolu: „nie wykraczaj poza równowagę”, co znaczyło, że nie można chcieć za wiele; „nie grzeb w ogniu mieczem”, czyli nie podżegaj ostrymi słowami rozgniewanego; „nie skub wieńca”, czyli nie występuj przeciw prawom, które są jak wieńce miast; „nie jedz serca” znaczy, że nie należy w sobie wzbudzać smutku; „nie siedź na mierze zboża”, czyli nie żyj bezczynnie; „nie obracaj się w drodze” – nie czepiaj się tego życia, kiedy umierasz. [Porfiriusz, Vita Pythagorae 42]

Trzystuosobowe stowarzyszenie pitagorejskie podporządkowało sobie na pewien czas Kroton. Później zwolennicy demokracji wzniecili bunt – i tu relacje przeczą sobie wzajem. Według jednych Pitagoras został, wraz z grupą uczniów, zabity; według innych po ucieczce zagłodził się na śmierć; istnieją też opowieści o jego śmierci na polu bitwy z Syrakuzańczykami.

Aczkolwiek po rozbiciu krotońskiego związku instytucjonalny pitagoreizm nie odżył, to przez następnych kilkaset lat wielu filozofów podawało się za kontynuatorów Pitagorasa. Ponieważ własne dokonania przypisywali mistrzowi, to nie da się dziś ustalić autorstwa poszczególnych idei. (Platon, który w swoim systemie w olbrzymiej mierze wykorzystał filozofię pitagorejską, wymienia Pitagorasa z imienia tylko dwukrotnie; Arystoteles, u którego pełno imion wcześniejszych filozofów, pisze zawsze „pitagorejczycy”.)

Nikt nie potrafi powiedzieć z pewnością, co mówił swym towarzyszom, gdyż milczenie było dla nich czymś zwyczajnym. Wszyscy jednak wiedzieli, że dusza, po pierwsze, jest według niego nieśmiertelna, a po wtóre, zmienia się w inne żywe stworzenia. Ponadto wydarzenia powtarzają się w pewnych cyklach i nic nigdy nie jest całkiem nowe. Mówił też, że wszystkie żywe istoty należy uważać za spokrewnione. Jak się zdaje, Pitagoras pierwszy przyniósł tę naukę do Grecji. [Porfiriusz, Vita Pythagorae 42]

Dziś większość specjalistów sądzi, że orfizm pojawił się przed Pitagorasem, a zatem zapożyczył on stamtąd doktrynę reinkarnacji, a nie dopiero wprowadził ją na helleński rynek idei. Natomiast był chyba pierwszy jeśli chodzi o – nie wspomniane w powyższym cytacie – badania nad matematycznymi harmoniami rządzącymi światem. Zacznijmy od wędrówki dusz.

Nasze prawdziwe je stanowi nie (widzialne) ciało, lecz (niewidzialna) dusza. Wprawdzie obecnie dusza zamieszkuje ciało, lecz dzieje się to wbrew jej naturze. Dusza jest boska i wieczna, w materialnym i śmiertelnym ciele znalazła się wskutek jakiejś winy, którą popełniła przed narodzinami. Po śmierci ciała trafia na sąd, który dusze złoczyńców kieruje na męki, a te, które czyniły dobro, umieszcza w krainie, gdzie zaznają licznych radości. Po pewnym czasie dusze znów łączą się z ciałami, zwierzęcymi bądź ludzkimi. Jeśli słynny wiersz Pindara z 476 r. p.n.e. wiernie oddaje wierzenia pitagorejskie, to

Wszyscy, którzy po trzykrotnym pobycie
Na jednym świecie i drugim
Potrafili zachować swą duszę zupełnie wolną od nieprawości,
Dochodzą drogą Zeusową do pałacu Kronosa.
Tam wyspę szczęśliwych oceaniczne owiewają zefiry (…)
A ich girlandami zdobią ramiona, wieńczą głowy.

Jesteśmy więc w stanie wyzwolić się z kręgu śmierci i ponownych narodzin – odzyskać utraconą boskość.

Jak dotąd wygląda to na czysty orfizm. Zasadnicza, jak się zdaje, różnica między pitagorejczykami a orfikami leżała w poglądach na to, jaka droga prowadzi do wyzwolenia. Orficy główny nacisk kładli na uczestnictwo w misteriach dionizyjskich: ekstatyczno-orgiastyczne obrzędy miały ich w jakiś cudowny sposób umożliwić duszy (od)zyskanie boskości. Pitagorejczycy za patrona obrali Apolla – i uważali, że oczyszczenie osiąga się przede wszystkim przez poznanie. Jeśli nawet przypisuje im się przestrzeganie dziwnych reguł, takich jak zakazy spożywania bobu lub chodzenia główną ulicą, albo nakaz zacierania śladu garnka w popiele, to może dlatego, że zbyt dosłownie rozumiano wspomniane już akusmata.

Droga poznania jest drogą filozofii – w rezultacie mieszały się ze sobą wiara i rozum. Oczyszczającą aktywnością rozumu miało być studiowanie matematyki. Powody pozostają niejasne. Być może w punkcie wyjścia – pośrednio potwierdzają to teksty Platona – jako środek oczyszczający stosowano muzykę. Po czym odkryto – co według dość zgodnej opinii miało wywrzeć na Pitagorasie ogromne wrażenie – że tajemnica harmonii muzycznych jest zawarta w czterech pierwszych liczbach. Jeśli mianowicie z dźwiękiem całej struny połączymy dźwięk tej samej struny skróconej o połowę – tzn. stosunek długości wyrażać się będzie jak 1 : 2 – to otrzymamy harmonijny interwał (oktawę). Inne harmonijne interwały dadzą nam stosunki długości struny 2 : 3 (kwinta) i 3 : 4 (kwarta).

Światem, stanowiącym jedną całość – wszystko jest tu ze wszystkim powiązane – rządzą niezmienne prawa, co przejawia się w regularnym następstwie pór roku, dni i nocy, powtarzalności niezliczonych zjawisk przyrodniczych. Pitagoras jako pierwszy miał określić świat mianem kosmos – w tym helleńskim słowie łączyły się pojęcia ładu, słuszności i piękna. I uznał, być może, że to, co ujawnia tajemnicę harmonii muzycznych – liczby 1, 2, 3 i 4 – kryje też w sobie tajemnicę kosmicznego ładu.

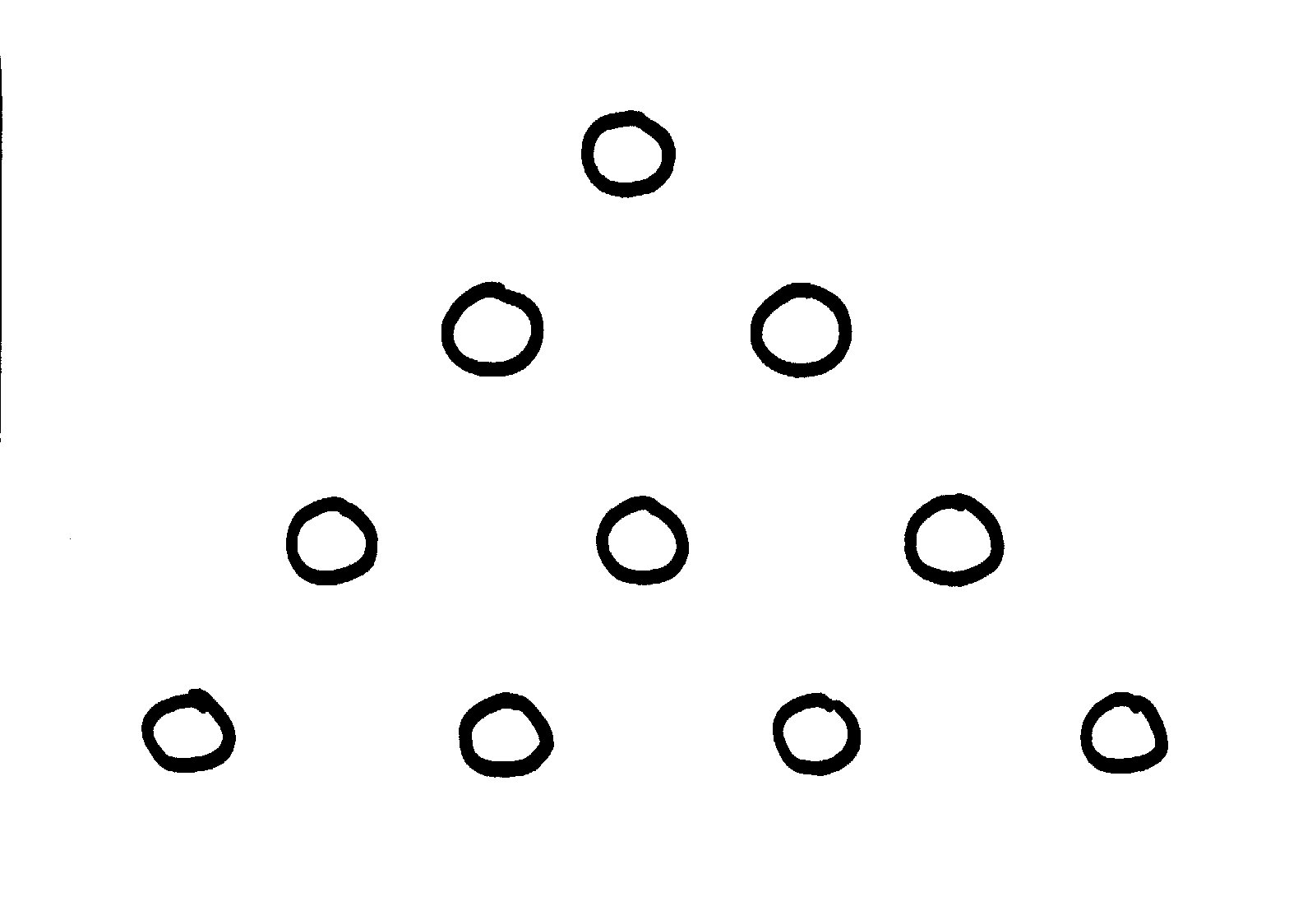Liczby w szkole pitagorejskiej przedstawiano rozkładając kamienie; w rezultacie miały one bezpośredni związek z przestrzenią. Jeden kamień wyznacza punkt, dwa kamienie oddalone od siebie prostą, trzy płaszczyznę, cztery (jeśli jeden z kamieni umieścimy ponad płaszczyzną wyznaczoną przez trzy pozostałe) bryłę. Jeśli rozłożymy jeden, dwa, trzy i cztery kamienie tak jak na rysunku, to otrzymamy złożony z dziesięciu kamieni pitagorejski tetraktys, święty symbol, „źródło i korzeń wiecznej natury”.

Tego typu spostrzeżenia tradycja wiąże z centralną tezą pitagorejczyków, iż arche stanowią liczby. I to – według pochodzącej z połowy IV w. p.n.e. relacji Arystotelesa – w podwójnym sensie: liczby są zarówno materią (tym, z czego rzeczy są zrobione), jak i wzorcami (tym, co rządzi powstawaniem, własnościami i zachowaniem rzeczy).

(…) tak zwani pitagorejczycy pierwsi zająwszy się naukami matematycznymi nauki te rozwinęli, a zaprawiwszy się w nich sądzili, że ich zasady są zasadami wszystkich rzeczy. Skoro tedy liczby zajmują pierwsze miejsce wśród tych zasad, a w liczbach, w większym stopniu niż w ogniu, ziemi i wodzie, można dostrzec, jak sądzili, wiele podobieństw do rzeczy istniejących i powstających – taka a taka własność liczb jest sprawiedliwością, inna jest duszą i rozumem, inna sprzyjającą okolicznością – i podobnie jest z każdą inną rzeczą; dostrzegli też w liczbach własności i proporcje muzyki; skoro więc wszystkie inne rzeczy wzorowane są, jak im się zdawało, w całej naturze na liczbach, a liczby wydają się pierwszymi w całej naturze, sądzili, że elementy liczb są elementami wszystkich rzeczy, a całe niebo jest harmonią i liczbą. [Arystoteles, Metafizyka I,5]

Zaraz dalej Arystoteles stwierdza, że doskonała jest, według pitagorejczyków, liczba 10 – a w związku z tym dziesięć jest krążących po niebie ciał, a także dziesięć par przeciwstawnych zasad (ograniczone-nieograniczone, parzyste-nieparzyste, jedność-wielość, prawe-lewe, męskie-żeńskie, spoczywające-ruchome, proste-krzywe, jasne-ciemne, dobre-złe, kwadratowe-podłużne). Pogląd o dziesięciu ciałach niebieskich, przypisywany Filolaosowi, zostanie omówiony poniżej, wtedy też wspomnimy o kluczowym dla pitagoreizmu podziale liczb na nieparzyste i parzyste.

Pozostaje pytanie o twierdzenie Pitagorasa: w trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów przyprostokątnych. Dla pitagorejczyków, o czym trzeba pamiętać, było to twierdzenie a charakterze nie arytmetycznym, ale geometrycznym: pole kwadratu zbudowanego na przeciwprostokątnej jest równe sumie pól kwadratów zbudowanych na przyprostokątnych.

Powyższe twierdzenie najprawdopodobniej znali wcześniej uczeni babilońscy, twierdzi się natomiast tu i ówdzie, że Pitagoras jako pierwszy je dowiódł. Nie możemy ani tego potwierdzić, ani temu zaprzeczyć. Nie wiemy też, jak mógł wyglądać pierwotny dowód. Żadne ze źródeł nie donosi natomiast, aby Pitagoras miał zwątpić w zasadę, że wszystko, co w tym świecie istnieje, da się w taki czy inny sposób sprowadzić do liczb naturalnych lub ich stosunków. Nic więc nie świadczy o tym, że to on, wykorzystując twierdzenie Pitagorasa, odkrył, iż długości przekątnej kwadratu o boku 1 nie da się wyrazić jako stosunku dwóch liczb naturalnych. (Co my wyrażamy mówiąc, że √2 jest liczbą niewymierną.)

14. Filolaos z Krotonu o budowie świata

Najwybitniejszym przedstawicielem pitagoreizmu w V w. p.n.e. był Filolaos z Krotonu (ok.470-ok.380 p.n.e.). Jego dzieło, zachowane w nielicznych fragmentach, uchodzi za pierwszy spisany wykład tej filozofii. Zawierało wyniki badań z zakresu embriologii, fizjologii i medycyny, wiązane, przez analogię, z rozważaniami o budowie świata jako całości. Były tam też rozważania o naturze muzyki i „harmonii sfer”. Tylko kosmologia Filolaosa będzie nas tu interesowała.

Wszystkie poznawane rzeczy mają w istocie liczbę, nic bowiem nie może być ani pomyślane, ani poznane bez niej. [Stobajos, Anthologium I,21]

Oto oczywisty wyraz pitagorejskiego programu badawczego. Liczby są parzyste, nieparzyste, a także – co dziś trudno pojąć – powstałe ze zmieszania tamtych parzysto-nieparzyste. Być może nieparzyste są „ograniczające”, a parzyste „nieograniczone”, ale o co tu chodzi, trudno powiedzieć. Niektórzy próbują rozumieć – po Demokrytejsku – przez „nieograniczone” próżnię, a przez „ograniczające” atomy. Praktyka układania z kamieni – niczym z atomów – figur, obrazujących liczby, w naturalny sposób prowadziła do przekonania, że próżnia – odstępy między kamieniami – jest tym, co liczby różnicuje:

Próżnia odróżnia bowiem i rozdziela kolejne rzeczy w szeregu. Zdarza się to przede wszystkim z liczbami, gdyż próżnia odróżnia ich naturę. [Arystoteles, Fizyka IV,6]

Wszechświat jest ograniczony, twierdził Filolaos – może za Parmenidesem lub Empedoklesem – i ma postać kuli. W samym jej środku znajduje się ogniste Jedno. Arystoteles wyjaśniał, że powodem umieszczenia ognia – a nie ziemi, jak u Anaksymandra i innych – w środku świata, było pitagorejskie przekonanie, że „ogień jest czcigodniejszy od ziemi” [O niebie II,13], jemu więc należy się miejsce centralne. Inny starożytny autor wskazywał na źródła tego pomysłu w biologii Filolaosa:

(…) nasienie jest ciepłe, a ono tworzy żywe istoty; miejsce złożenia nasienia (czyli macica) także jest ciepłe (…) natychmiast po narodzinach żyjąca istota wciąga zewnętrzny oddech, który jest zimny; później, jakby z konieczności, wyrzuca go. [Menon w: Anon. Londinensem XVIII,8]

Może więc obraz był taki, że z Ognia Centralnego rodzi się świat, który jako całość jest ożywiony. Po narodzinach zaczyna oddychać otaczającą go próżnią, co (odróżniając liczby) oddziela rzeczy w jego obrębie, przypisując każdej należne jej miejsce. W ten sposób powstaje dziesięć ciał niebieskich, otoczonych znów sferycznym ogniem:

Filolaos umieścił ogień wokół środka, nazywając go „ogniskiem świata”, „domem Zeusa” i „ołtarzem, więzią i miarą natury”. Później znów jest inny ogień w górze, otaczający. Ale mówi, że pierwszy z natury jest środek, a wokół niego tańczy dziesięć boskich ciał – kula stałych gwiazd, po niej pięć planet, później słońce, potem księżyc, po nim ziemia, z kolei przeciw-ziemia, wreszcie ogień ogniska, mający miejsce w środku. [Aetios, Placita philosophorum II,7]

Przeciw-ziemia została dodana po to, aby ciał niebieskich było dziesięć. Filolaos umieścił na Przeciw-ziemi krainę umarłych, Hades z poematów Homera (Ogień Centralny odpowiadał chyba Tartarowi).

Ziemia, krążąc wokół Ognia Centralnego po okręgu, jest zawsze odwrócona od niego stroną zamieszkaną – tak że nigdy „domu Zeusa” nie widzimy. Słońce, które również krąży po okręgu wokół środka świata, jest rodzajem lustra, odbijającym światło i ciepło Ognia Centralnego.

Wirują też nieustannie planety i kula gwiazd stałych. Każde z poruszających się ciał niebieskich miało wydawać dźwięk, o wysokości określonej przez prędkość jego ruchu.

Założywszy to oraz że prędkości, mierzone na podstawie odległości, mają proporcje akordów, [pitagorejczycy] mówią, że dźwięk powstający z gwiazd poruszających się po okręgu jest harmonią. Wydaje się jednak dziwne, że tego dźwięku nie słyszymy. Podają więc jako przyczynę, że towarzyszy nam od samych narodzin i nie odróżniamy go od przeciwnej mu ciszy. Rozpoznajemy bowiem dźwięki i ciszę dzięki wzajemnemu przeciwieństwu. [Arystoteles, O niebie II,9]

Jedynym człowiekiem, słyszącym niebiańskie dźwięki, miał być Pitagoras.

15. Pierwsi pitagorejscy matematycy

Kwadraty, prostokąty, trójkąty i inne figury układane z kamieni przez pitagorejczyków, a także spekulacje na temat roli liczb parzystych i nieparzystych, dały początek teoretycznej matematyce. Spośród czterech działów matematyki, jakie wyróżniali Hellenowie – arytmetyki, geometrii, astronomii i muzyki – najpierw rozwinęła się geometria, potem geometryczna astronomia. Obie osiągnęły do II w. p.n.e. taki poziom zaawansowania, że dalszy postęp w tych dziedzinach dokonał się dopiero w nowożytnej Europie. W arytmetyce – ze względu chyba na nieporęczne systemy zapisu liczb, a bardziej jeszcze na brak w helleńskim myśleniu zera – osiągnięto znacznie mniej. Teoretyczna refleksja nad muzyką nie wykroczyła poza pitagorejskie odkrycie kryjących się za akustycznymi harmoniami stosunków 1/2, 2/3, 3/4 (tercję, podlegającą stosunkowi 5/6, odkryto dopiero w XVII w.).

Historię wczesnej matematyki helleńskiej spisał przed 300 r. p.n.e. jeden z bliskich towarzyszy Arystotelesa, Eudemos z Rodos. Jego dzieło zaginęło, ale powołują się na nie liczni autorzy aż do Simplikiosa (VI w.) i dzięki tym przekazom stanowi ono nasze podstawowe źródło wiedzy o dokonaniach pierwszych geometrów.

Ojnopides z Chios (ok.490-420 p.n.e.) miał jako pierwszy ustanowić regułę, że konstrukcje czysto geometryczne to te, których dokonuje się przy użyciu jedynie linii i cyrkla. Ten warunek został zapewne sformułowany pod wrażeniem pewnych osiągnięć. Ojnopides miał wykazać, że za pomocą linii i cyrkla można wykreślić przechodzącą przez dany punkt prostą prostopadłą do prostej danej. Dało to początek badaniom, w trakcie których rychło natrafiono na zagadnienia – jak my dziś wiemy – metodami geometrycznymi nierozwiązywalne. Chodzi zwłaszcza o problemy kwadratury koła, podwojenia sześcianu i trysekcji kąta. Usiłując rozwiązać zadania nierozwiązywalne, helleńscy geometrzy dokonali wielu odkryć o epokowym znaczeniu.

Tradycyjnie Pitagorasowi przypisano odkrycie sposobu dokonania kwadratury trójkąta, prostokąta i niektórych wieloboków wypukłych. Chodziło o wykreślenie, metodami geometrycznymi, kwadratu o polu powierzchni równym polu danej figury. Teraz powstał problem, jak za pomocą linii i cyrkla narysować kwadrat o polu powierzchni równym polu danego koła.

(W pochodzącym z ok. 1650 r. p.n.e. egipskim papirusie – będącym kopią tekstu o dwieście lat starszego – znajdujemy regułę, że kwadrat o polu powierzchni równym polu danego koła powinien mieć bok równy 8/9 jego średnicy. Dawałoby to w świetle – nieznanego Egipcjanom – wzoru na pole powierzchni koła wartość liczby π ok. 3,16. W ten sposób dokonano kwadratury koła z dokładnością do ok. 0,7%, co dla celów praktycznych było całkowicie wystarczające. Ale helleńskiego geometry-teoretyka taki wynik zadowolić nie mógł: on szukał rozwiązań ścisłych i dowiedzionych.)

Antyfon Sofista (480-411 p.n.e.) był wybitnym retorem; nie jest jasne, czy nad kwadraturą koła pracował on, czy ktoś inny o tym samym imieniu. Miał jako pierwszy posłużyć się tzw. metodą wyczerpywania: wpisywał w koło serię wielokątów foremnych o wciąż rosnącej liczbie boków, a zatem coraz bardziej przypominających okrąg. Był, zdaje się, przekonany, że przy odpowiednio dużej liczbie boków okrąg i wielokąt pokryją się.

Hippokrates z Chios (ok.470-ok.410), autor Elementów geometrii (dzieła zaginionego, jednak wielu historyków matematyki podejrzewa, że jego obszerne fragmenty weszły do ksiąg I i II Elementów Euklidesa), ponoć jako pierwszy wykazał, że pole powierzchni koła jest proporcjonalne do kwadratu jego promienia. (Jeśli dowód przedstawiony przez Euklidesa pochodzi z jego zaginionego tekstu, to Hippokrates przeprowadził go metodą wyczerpywania.) Dowiódł też, zapewne w podobny sposób, że stosunki pól powierzchni podobnych segmentów kół są takie, jak stosunki kwadratów ich podstaw. Następnie dokonał kwadratury niektórych „księżyców”, zwłaszcza takiego, jak przedstawiony na rysunku.

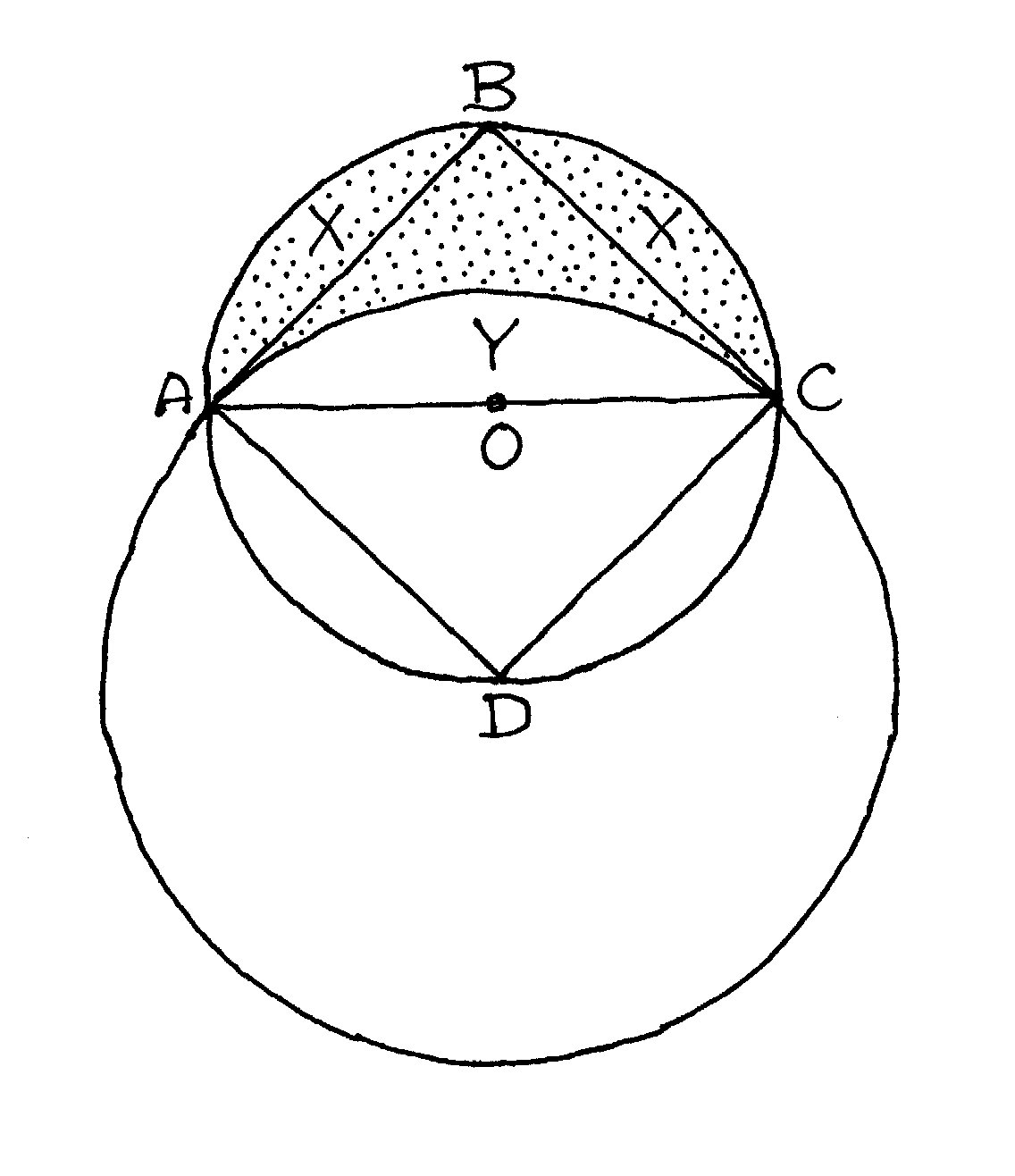W koło o środku O wpisano kwadrat ABCD. Księżyc (na rysunku obszar zakropkowany) otrzymano wycinając z koła o środku O fragment za pomocą koła o środku D i promieniu AD. Ponieważ oba kąty AOB i ADC są proste, to segmenty X i Y są podobne. Z twierdzenia Pitagorasa wynika, że 2 AB² = AC², a zatem, na mocy twierdzenia wspomnianego przed chwilą, pole powierzchni obu segmentów X jest łącznie takie, jak pole Y. Ponieważ księżyc otrzymano z trójkąta ABC odejmując od niego Y i dodając 2X, to pole powierzchni księżyca jest równe polu trójkąta ABC – czyli połowie pola kwadratu ABCD. Hippokrates dokonał też kwadratury księżyców o zewnętrznym obwodzie mniejszym lub większym od półkola, ale zawsze o specjalnie dobranym promieniu drugiego obwodu. Do pełnego koła przejść, rzecz jasna, nie zdołał.

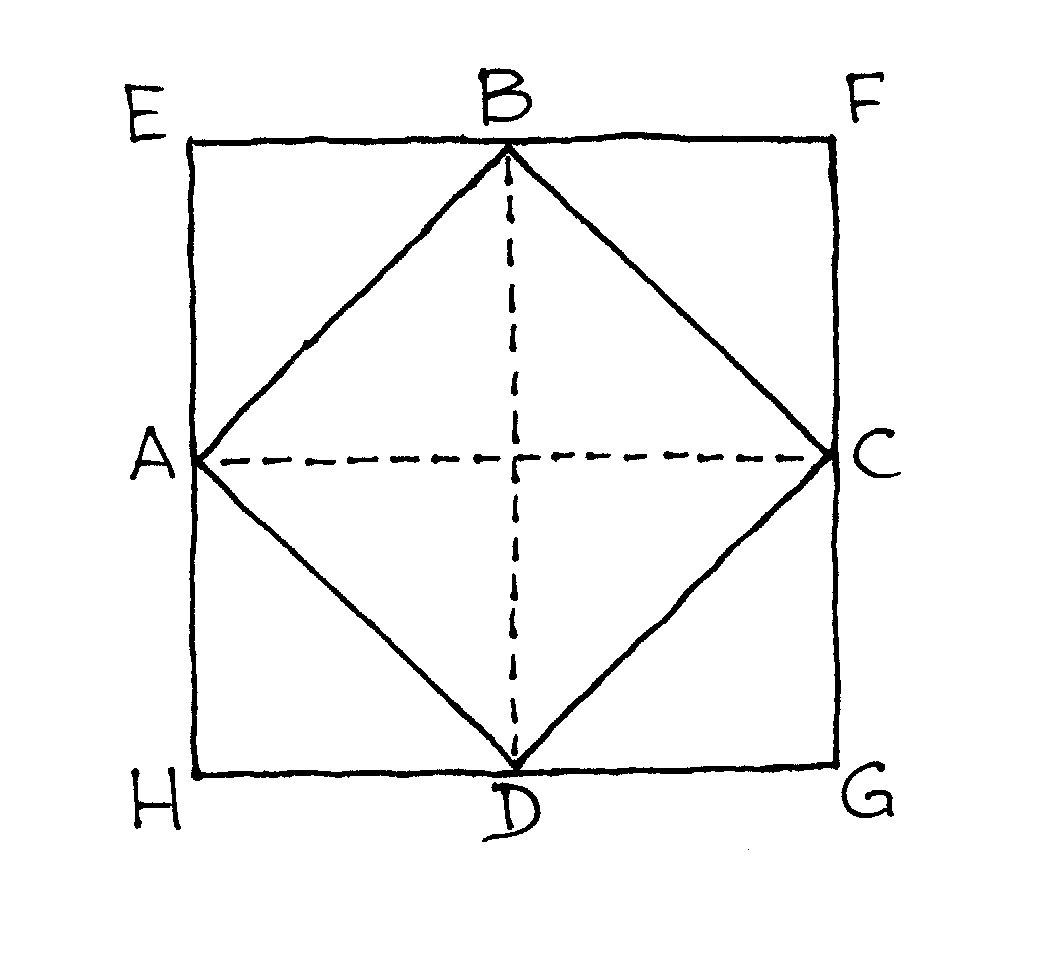Wykreślenie kwadratu o polu powierzchni równej połowie pola kwadratu danego ABCD jest trywialne: jest to kwadrat EFGH, którego wierzchołkami są środkowe punkty boków tamtego kwadratu. (Że tak jest, pomogą ujrzeć dodane na rysunku linie przerywane.)

Zapytano z kolei, jak metodami geometrycznymi wyznaczyć długość x krawędzi sześcianu, który ma objętość dwukrotnie mniejszą lub większą od objętości sześcianu o boku a. Hippokrates zdołał zredukować to zadanie do problemu wyznaczenia dwóch średnich proporcjonalnych x i y między a i 2a. Wartość tych średnich x i y określa wzór a/x = x/y = y/2a. Uzasadnienie jest trywialne: stosunek objętości obu sześcianów o bokach a i x wynosi a³/x³ = (a/x)(x/y)(y/2a) = 1/2. Oczywiście nie pozwoliło to uzyskać rozwiązania problemu nierozwiązywalnego, ale otworzyło drogę do dalszych, płodnych badań matematycznych.

Pitagorejczyk Teodor z Cyreny (465-398 p.n.e.) był czas jakiś nauczycielem Platona, który na jego temat zapisał:

O kwadratach coś nam Teodor pisał i o tym, co miał trzy stopy kwadratowe, oraz o tym, co miał pięć stóp kwadratowych powierzchni, dowodził nam, że co do długości boku nie są współmierne z jednostopowym i tak po jednym każdy kwadrat brał pod uwagę aż do siedemnastostopowego; na tym się jakoś zatrzymał. [Platon, Teajtet 147D]

Skoro wyliczenie zaczyna się od kwadratu o powierzchni 3, to najwyraźniej odkrycie, że √2 jest liczbą niewymierną, nastąpiło przed Teodorem (żadne ze źródeł nie donosi, kto tego dokonał).

Standardowy dowód tego ostatniego twierdzenia wygląda następująco. Załóżmy, że istnieją liczby naturalne p i q, takie że √2 = p/q. Jedna z tych liczb musi być nieparzysta, w przeciwnym bowiem razie ułamek ten można by skrócić przez 2 i ewentualnie kontynuować procedurę skracania dopóki nie doszlibyśmy do co najmniej jednej liczby nieparzystej. Podnosząc obie strony równania do kwadratu i mnożąc przez q² otrzymujemy 2q² = p². Skoro po lewej stronie mamy liczbę parzystą, to p jest parzyste (gdyż kwadrat każdej liczby nieparzystej jest nieparzysty). Kwadrat liczby parzystej jest podzielny nie tylko przez 2, ale i przez 4, a zatem po podzieleniu obu stron równania przez 2 otrzymujemy po prawej stronie liczbę parzystą, a po lewej samo q². Tak więc q jest parzyste. Doszliśmy do absurdu, co prowadzi do wniosku, że nie istnieją liczby naturalne p i q spełniające powyższe równanie.

Dowód ten łatwo uogólnić na wszystkie liczby naturalne nie będące liczbami kwadratowymi. Tymczasem Teodor miał po kolei dowodzić, że – w dzisiejszej terminologii – √3 jest liczbą niewymierną, √5 jest liczbą niewymierną, i tak dalej do √17. Używał więc jakiejś innej techniki dowodzenia, co rodzi podejrzenie, że pierwotny dowód niewymierności √2 był odmienny od przedstawionego powyżej. Istnieją hipotezy co do tego, jakiego rozumowania można było użyć dla dowodzenia niewymierności pierwiastka każdej z liczb „niekwadratowych” z osobna, tu jednak je pominiemy. Podkreślmy tylko, że było to zapewne rozumowanie o charakterze raczej geometrycznym niż arytmetycznym. Samo twierdzenie Pitagorasa, którego zastosowanie prowadziło do odkrycia odcinków niewspółmiernych (raczej niż liczb niewymiernych), dotyczyło w rozumieniu Hellenów nie sumowania kwadratów liczb, ale sumowania pól powierzchni kwadratów zbudowanych na bokach trójkąta prostokątnego.

Za pomocą linii i cyrkla łatwo podzielić kąt na połowę. Kto jako pierwszy tego dokonał, nie wiadomo. Rychło zapytano, w jaki sposób można podzielić kąt na trzy równe części.

Hippiasz z Elis (ok.460-ok.400 p.n.e.) opisany został przez Platona jako człowiek próżny i arogancki. Wędrując od miasta do miasta prowadził wykłady na temat poezji, gramatyki, historii, polityki, archeologii, matematyki i astronomii. Miał wynaleźć krzywą za pomocą której można podzielić kąt na dowolną ilość równych części. Jest to tzw. kwadratrysa, opisana w IV księdze Synagoge Papposa z Aleksandrii (I poł. IV w. n.e.), a przedstawiona na rysunku.

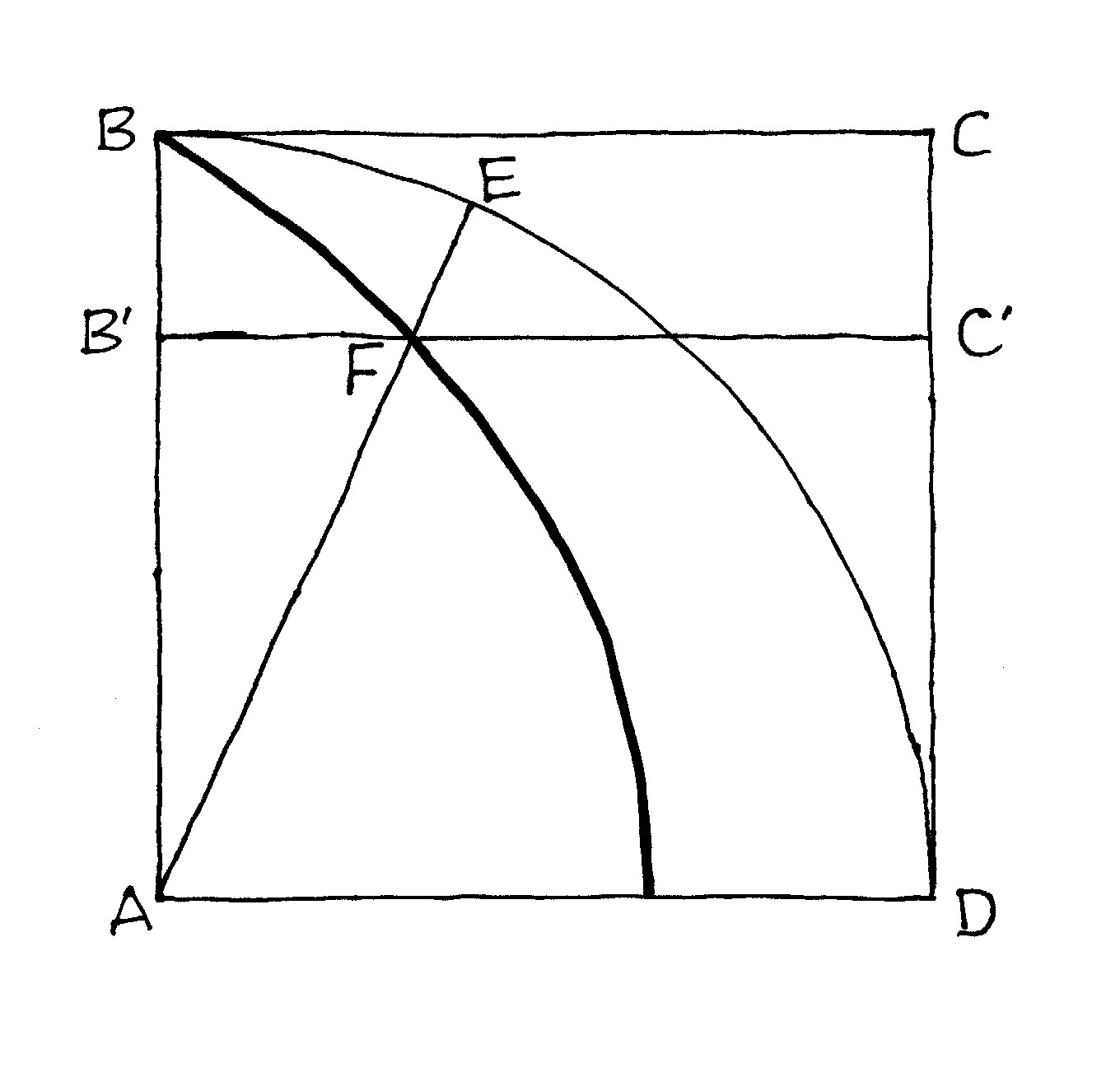BED to ćwiartka okręgu o środku A. Punkt E porusza się ruchem jednostajnym po obwodzie okręgu od B do D, a punkty B' i C' poruszają się ruchami jednostajnymi od, odpowiednio, B do A i C do D, tak aby punkty E i C' dotarły do D, a B' do A, w tej samej chwili. Kwadratrysa to zbiór punktów F otrzymanych z przecięć obracającego się promienia AE i poruszającego się odcinka C'D'.

Co w ten sposób osiągnięto? W czasie, gdy promień AE obraca się o równe kąty, punkty C' i D' przebywają równe drogi, a zatem rzutując punkty kwadratrysy na oś CD rzutujemy na tę oś kąty DAE w skali liniowej. I na odwrót: punkty kwadratrysy przyporządkowują równe odcinki osi CD równym kątom DAE. Podział danego odcinka na n równych części jest metodami geometrycznymi łatwo wykonalny. Jeśli teraz podzielimy odcinek C'D na np. trzy równe części i znajdziemy punkty kwadratrysy odpowiadające temu podziałowi, to przechodzić będą przez nie ramiona kątów dzielących kąt DAE na trzy kąty równe. Kwadratrysy nie da się jednak wykreślić za pomocą linii i cyrkla (choć można metodami geometrycznymi wyznaczyć jej przebieg z dowolną dokładnością).

Bryson z Heraklei urodził się ok. 450 r. p.n.e. Arystoteles krytykuje jego metodę kwadratury koła, ale nie pisze, na czym polegała. W komentarzu Aleksandra z Afrodyzji (ok. 200 r. n.e.) czytamy, że jeden kwadrat wpisał on w koło, drugi na nim opisał, a trzeci umieścił między nimi – brak jednak dalszych wyjaśnień. Temistiusz (IV w. n.e.) przypisuje natomiast Brysonowi twierdzenie, że pole powierzchni koła jest mniejsze niż pole dowolnego wielokąta opisanego na kole i większe niż pole dowolnego wielokąta weń wpisanego, zaś różnica zmniejsza się wraz ze wzrostem liczby boków. Pozwalałoby to na dokonanie kwadratury koła z dowolną, choć nigdy zupełną, dokładnością.

Do tego czasu, co warto podkreślić, problem kwadratury koła wszedł do świadomości publicznej, o czym świadczy fakt, że wspomina o nim Arystofanes w napisanej w 414 r. p.n.e. komedii Ptaki.

4. Matematycy IV w. p.n.e.

Archytas z Tarentu (ok.428-ok.350 p.n.e.), uczeń Filolaosa z Krotonu, był matematykiem, filozofem i politykiem. Ponoć ocalił Platona z rąk Dionizjosa. Twierdził, że rozumowanie matematyczne łagodzi obyczaje i sprzyja wzrostowi sprawiedliwości społecznej. Matematykę dzielił na geometrię, arytmetykę, astronomię i muzykę (co w średniowieczu stanowiło podstawę klasyfikacji czterech ze „sztuk wyzwolonych”).

Parając się zagadnieniem podwojenia objętości sześcianu wprowadził do geometrii ruch: używał półkola obracającego się w trójwymiarowej przestrzeni i krzywej otrzymanej z jego przecięć z pewną trójwymiarową powierzchnią. Uzyskał też ciekawe wyniki na temat nieistnienia pewnych średnich geometrycznych. Niestety, jego prace znamy głównie z niekompletnych uwag w komentarzach, jakie do dzieł Archimedesa napisał Eutokios z Askalonu (I poł. VI w.). Ale niektórzy twierdzą, że VIII księga Elementów Euklidesa oparta jest w dużej mierze na dokonaniach Archytasa, zaś księga VII zawiera szereg twierdzeń, z których korzystał pitagorejczyk z Tarentu.

Ponoć skonstruował mechanicznego ptaka poruszanego przez strumień pary, a także (za co chwali go w Polityce Arystoteles) grzechotkę dla dzieci.

Archytas miał też dowodzić, że świat jest przestrzennie nieskończony. Gdyby, jak twierdziła większość myślicieli helleńskich i hellenistycznych, świat miał granice, to dotarłszy do nich można by przecież wyciągnąć rękę i sięgnąć poza nie, a tam przecież musi być jakieś ciało lub przestrzeń jako „to, w czym ciało jest lub może być”. Ponieważ tę procedurę można kontynuować bez końca, to „musi istnieć ciało i przestrzeń rozciągające się bez granic” [Simplikios, Physicorum libros].

Teajtet z Aten urodził się ok. 415 r. p.n.e., zmarł zapewne w 369 r. p.n.e. wskutek ran odniesionych w bitwie Aten z Koryntem. Nie wiemy, jak blisko był związany z Akademią, ale Platon jego imieniem nazwał jeden z dialogów, zaś w Sofiście i Timajosie uczynił go głównym mówcą.

Jego ogromnie cenione prace na temat liczb wymiernych i niewymiernych zaginęły, ale niektórzy twierdzą, że Księga X Elementów Euklidesa, wyraźnie różniąca się stylem rozważań od reszty tekstu, jest w całości dziełem Teajteta.

Pitagoras znał ponoć trzy wielościany foremne, czyli takie, (1) których wszystkie ściany są identycznymi figurami foremnymi, (2) w każdym wierzchołku zbiega się taka sama liczba ścian i (3) które są wypukłe. Były to czworościan i ośmiościan (zbudowane z czterech i ośmiu trójkątów równoramiennych zbiegających się w wierzchołkach odpowiednio po trzy i po cztery), a także sześcian (czyli zbudowana z kwadratów kostka). Pitagorejczyk Hippazos ok. 465 r. p.n.e. miał wspomnieć o „sferze z 12 pięciokątów”, (co niemal z pewnością odnosi się do dwunastościanu foremnego zbudowanego z foremnych pięciokątów zbiegających się w wierzchołkach po trzy). W takim razie Teajtetowi pozostawałoby do odkrycia, że istnieje jeszcze dwudziestościan foremny (zbudowany z trójkątów równobocznych zbiegających się w wierzchołkach po pięć). Źródła mówią, że dowiódł on, iż więcej wielościanów foremnych – zwanych czasem „bryłami platońskimi”, gdyż na nich oparty jest „matematyczny atomizm” z kart Timajosa – niż wymienione pięć nie ma. Według powszechnej opinii Księga XIII Elementów Euklidesa oparta jest głównie na dokonaniach Teajteta.

Tymaridas z Paros (ok. 400-ok. 350 p.n.e.) miał badać liczby pierwsze, które nazwał „liniowymi”, jako że nie dawało się ich przedstawić w postaci zbioru kamieni ułożonych w prostokąt. Są to, inaczej mówiąc, te liczby naturalne, które nie są podzielne przez liczby naturalne różne od siebie (1 zwykle nie było przez Hellenów nazywane liczbą; Tymaridas określał je mianem „ilości granicznej”). Są to kolejno 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ... . W szeregu liczb naturalnych liczby pierwsze występują coraz rzadziej, gdyż – mówiąc potocznie – im dalej tym więcej okazji do bycia podzielną przez którąś z mniejszych liczb. Powstaje w związku z tym pytanie, czy istnieje największa liczba pierwsza.

W księdze X Elementów Euklidesa znajdujemy dowód, iż liczb pierwszych jest nieskończenie wiele. Każda liczba nie-pierwsza da się przedstawić jako iloczyn liczb wyłącznie pierwszych (np. 8 = 2 x 2 x 2, 654 = 2 x 3 x 109). Jeśli teraz weźmiemy dowolny skończony zbiór X liczb pierwszych, to można je wszystkie przez siebie pomnożyć i do wyniku dodać 1. Otrzymana liczba nie będzie podzielna przez żadną z liczb z naszego zbioru, bo zawsze zostanie 1 reszty. Będzie więc albo nową liczbą pierwszą, albo będzie podzielna przez liczbę pierwszą nie należącą do zbioru X. Jakkolwiek byłby więc ów zbiór liczny, to zawsze istnieć będzie liczba pierwsza do tego zbioru nie należąca i tak dalej bez końca. Ale czy taki dowód podał Tymaridas, czy może dopiero Euklides, nie wiemy.

Tymaridas podał też wzór na rozwiązywanie pewnych układów n równań liniowych zawierających n zmiennych.

Dinostratos (ok.390-ok.320 p.n.e.) ponoć jako pierwszy użył kwadratrysy Hippiasza z Elis do przeprowadzenia kwadratury koła. Punkt G, w którym kwadratrysa przecina odcinek AD (zob. rys. w § I.12), w zasadzie nie istnieje – bo wtedy linie AF i C'D' na chwilę się pokrywają – ale można go wyznaczyć z dowolną dokładnością jako punkt graniczny. Stosunek długości łuku AED do promienia okręgu AB jest równy stosunkowi AB do AG. A zatem obwód całego okręgu jest równy 4 AB²/AG. To, że obwód został wyrażony jako stosunek długości odcinków, pozwala wykreślić kwadrat o polu powierzchni równym polu danego koła. Ale, podobnie jak trysekcja kąta w wykonaniu Hippiasza, nie była to konstrukcja wykonalna za pomocą tylko linii i cyrkla.

Menajchmos (ok. 380-ok. 320 p.n.e.), był uczniem Eudoksosa. Wcześniej Hippokrates zredukował problem podwojenia objętości sześcianu do znalezienia dwóch średnich proporcjonalnych. Borykając się z tym drugim zagadnieniem Menajchmos badał przecięcia stożka z płaszczyzną nachyloną do płaszczyzny podstawy – i opisał krzywe nazwane potem elipsą, parabolą i hiperbolą. Podobno pracował też nad udoskonaleniem matematycznego modelu ruchów ciał niebieskich Eudoksosa, jednak żadne bliższe informacje na ten temat do nas nie dotarły.

Aristajos Starszy (ok. 370-ok.300 p.n.e.) miał napisać cenione dzieło o przecięciach stożkowych w pięciu księgach, a także pracę o porównywaniu wielościanów foremnych. W tej drugiej dowiódł m.in., że w przypadku dwunastościanu i dwudziestościanu wpisanych w tę samą sferę, okręgi opisane na pięcioboku i na trójkącie, tworzących ich ściany, mają identyczne promienie.

Autolykos z Pitane (ok. 360-ok.290 p.n.e.) był ponoć autorem pracy o geometrii sfery, a także traktatu O wschodach i zachodach. W obu miał poruszać zagadnienia związane z matematycznym modelem nieba Eudoksosa, ale żadnych szczegółów nie znamy.

strona główna